1. 서론
현재 다양한 분야에서 활용되고 있는 딥러닝 시스템을 학습시키기 위해서는 원본과 정답 영상의 쌍으로 이루어진 훈련 데이터가 필요하다. 특히, 의료 영상의 경우, 일반적인 영상에 비해 정답 영상이 포함된 훈련 데이터를 만들거나 구하는 것이 어렵다. 정답 영상을 만들기 위한 해부학적 전공지식이 수반되지 않으면 정확한 정답영상을 만들 수 없으며 의료 영상에 영상 편집 도구를 이용하여 장기의 종류를 표시하는 라벨링(labeling) 과정이 의료인들에게 노동집약적이므로 대량의 훈련 데이터를 쉽게 생성하기 힘들기 때문이다.
너무 적은 양의 훈련 데이터로 딥러닝 모델을 학습시키게 되면 과적합(overfitting) 문제로 인해 학습 후 테스트 데이터를 제대로 판별하지 못하게 될 수 있다 [1]. 소량의 데이터로 딥러닝 모델을 학습시키기 위해서 다양한 방법이 연구되고 있지만, 가장 널리 사용되는 방법 중의 하나가 바로 데이터 증강법(data augmentation)이다 [2,3,4]. 데이터 증강법이란, 원본 훈련 데이터를 기반으로 새로운 데이터를 만드는 과정을 말한다.
기존 연구에서는 영상 분할 모델의 데이터 증강을 위해서 아핀 변환(평행이동, 회전, 크기변환), 일정 영역 자르기(crop), 반전, 노이즈 추가 [2, 3] 혹은 영상 와핑(image warping) [5], GAN(Generative Adversarial Network) [4] 같은 방법들이 사용되어 왔다. 그러나 이와 같은 영상의 내용을 고려하지 않은 ‘임의적인 변환’ 들에 의한 데이터 증강법은 자칫 실제 의료 데이터에 내포된 해부학적, 생물학적 구조를 해칠 수 있는 위험이 있다. 그리고 이렇게 만들어진 데이터로 학습시킨 영상 분할 모델은 현실의 데이터에서 높은 성능을 보이지 못할 가능성이 있다. 따라서 본 연구에서는 해부학적으로 유의미한 CT 영상 변형을 통해 딥러닝 모델의 성능을 향상시키는 데이터 증강법을 제안하고, 기존 연구의 임의적인 변환들로 딥러닝 영상분할 모델을 학습시켰을 때의 성능을 각각 측정하였다. 그 결과, 본 연구의 데이터 증강 방법이 노이즈가 심한 의료 영상에서 영상분할 성능 향상을 보이는 것을 실험 데이터에 대해 확인하였다.
본 연구에서는 대퇴골을 이용하여 영상 분할 성능을 측정하려고 한다. CT 영상에서 대부분의 대퇴골 영역은 다른 신체 부위와 뚜렷한 경계를 이루고 있어서 기본적인 영상 분할 알고리즘으로도 높은 성능을 쉽게 얻을 수 있다. 그러나 연골로 덮인 부분 주위에서는 경계가 흐릿하여 기존의 방법으로는 매끄러운 영상분할 결과를 얻기 힘들기 때문이다.
본 논문의 구성은 다음과 같다. 2장에서 전체 과정에 대해서 살펴본 후, 3-6장에서는 CT 영상으로부터 삼차원 삼각형 메쉬 추출, 계층적 면 군집화(hierarchical face clustering)을 이용한 메쉬 분할, 메쉬 변형, 그리고 변형된 메쉬를 이용한 CT 영상 와핑을 차례로 설명한다. 7장에서는 실험 결과에 대해서 살펴보고 마지막으로 8장에서 결론을 짓고 향후 연구 방향에 대해서 논의한다.
2. 전체 과정
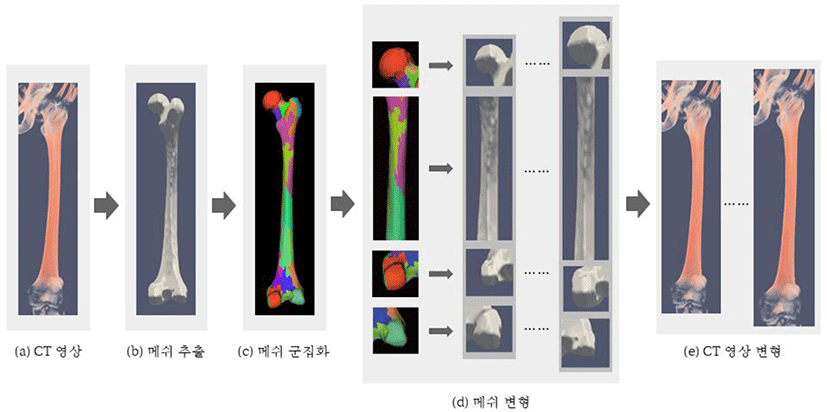
데이터 증강 과정은 다음과 같이 크게 메쉬 추출, 계층적 면 군집 분석을 이용한 메쉬 분할, 메쉬 변형, CT 영상 변형, 그리고 마지막으로 딥러닝 기반의 영상분할 모델 학습으로 진행된다 (Figure 1 참고).
-
메쉬 추출: CT 영상으로부터 데이터 증강의 토대가 되는 삼차원 삼각형 메쉬 모델을 얻는다. 본 연구에서는 CT 영상에서 대퇴골 영역을 분할하는 것이 목적이므로, 대퇴골 부위의 메쉬를 추출하였다.
-
계층적 면 군집화를 이용한 메쉬 분할: 모델의 해부학적 특성을 반영하여 메쉬를 변형하기 위해 곡률 기반의 형태 분석과 면 군집화(face clustering)를 통해 메쉬를 의미 있는 부분들로 나눈다.
-
메쉬 변형: 대퇴골 각 부위별 크기의 통계 수치를 이용하여 각 부위에 적용할 변형 파라메터를 자동으로 생성하고, 이를 바탕으로 단일 메쉬로부터 다수의 변형된 메쉬를 자동으로 생성한다.
-
CT 영상 와핑: 변형 전후 메쉬의 정점들 간의 위치 이동 벡터(displacement vector)를 CT 영상의 모든 영역에 대해 보간하고, 보간된 위치 이동 벡터를 이용하여 원본 CT 영상의 각 복셀(voxel)을 이동한다. 이 과정을 통해 다수의 변형된 메쉬들부터 다수의 와핑된 CT 영상을 얻을 수 있다.
딥러닝 기반의 영상분할 모델 학습 과정에서는 본 연구의 데이터 증강방법과 ‘임의적인 변환’ 들을 이용한 데이터 증강법으로 각각 훈련 데이터를 증강한 후, 각각의 훈련 데이터를 이용하여 영상분할 모델을 학습시키고, 성능을 비교하였다.
3. 메쉬 추출
CT 영상에 대퇴골 부위가 라벨링되어 있는 경우, 라벨링된 복셀 집합으로부터 마칭 큐브(marching cubes) 알고리즘 [6]을 적용하여 삼차원 삼각형 메쉬를 추출할 수 있다. 그러나 데이터 수집 과정에서 얻은 대부분의 CT 영상에는 대퇴골이 표시되어 있는 정답 영상이 포함되어 있지 않다. 원래대로라면 전문적인 해부학적 지식을 가진 의료인이 만든 정답 영상을 써야 하지만, 본 연구는 학습 성능의 향상을 실험적으로 증명하는 것이 목적이므로 연구자 본인이 직접 정답 영상을 라벨링하였다. 훈련 데이터의 모든 픽셀에 일일이 수작업으로 라벨링을 하는 것은 비효율적이므로 반자동적 알고리즘을 사용하였다. 먼저, MITK-GEM [7]을 사용하여 일부의 대퇴골 픽셀들을 라벨링한 후, 해당 프로그램의 삼차원 그래프 컷(3D graph cut) 알고리즘을 이용해서 대퇴골과 배경에 대한 정답 영상을 얻어 삼차원 삼각형 메쉬를 추출하였다.
4. 계층적 면 군집화를 통한 메쉬 분할
대퇴골 각 부위의 크기에 대한 통계 [8]를 보면 사람마다 대퇴골의 형태나 각 부위 간의 비율에 차이가 있다는 사실을 알 수 있다. 대퇴골 모델 전체에 대해서 동일한 변형을 적용하게 되면 이와 같은 해부학적 특성을 반영할 수가 없다. 대퇴골 각 부위별로 다르게 변형하기 위해서는 먼저 메쉬를 각 부위별로 나누어야 한다. 각 대퇴골의 각 부위를 살펴보면 골두는 구와, 그리고 대퇴골체는 원기둥과 같이 기본 도형과 유사한 형태를 띄고 있다는 것을 직관적으로 알 수 있다. 따라서 본 연구에서는 표면의 국소적 경향이 유사한 부위끼리 군집화하여 대퇴골의 각 부위를 나누었다. 이를 위해 본 논문에서는 Lee가 제시한 방법 [9]을 사용하였다.
먼저, 메쉬 국소 표면의 기하학적 특성을 알아내기 위해서 메쉬 표면의 주곡률로부터 형태 인덱스(shape index)와 굴곡도(curvedness) [10]를 계산하였다. 주곡률로도 군집분석을 할 수는 있지만 주곡률은 값의 범위가 너무 크고 최대곡률과 최소곡률을 동시에 쓰지 않으면 국소 부위의 기하학적 특성을 바로 알아내기 어렵다. 형태 인덱스는 (1,-1)사이의 값으로 삼차원 표면이 어떤 형태에 가까운지를 판별하게 하며 굴곡도는 표면의 굴곡의 정도를 판별하기 위한 값으로 다음과 같이 정의된다 [1].
이때, κ1 와 κ2 각각 최소 곡률과 최대 곡률을 나타낸다. 군집 분석을 수행했을 때 울퉁불퉁한 메쉬의 표면이나 사소한 구조물이 군집분석 알고리즘에 미치는 영향을 줄이기 위해서 메쉬에 meanshift 알고리즘 [11]으로 형태 인덱스와 굴곡도의 잡음을 필터링하였다. (Figure 2 참조)
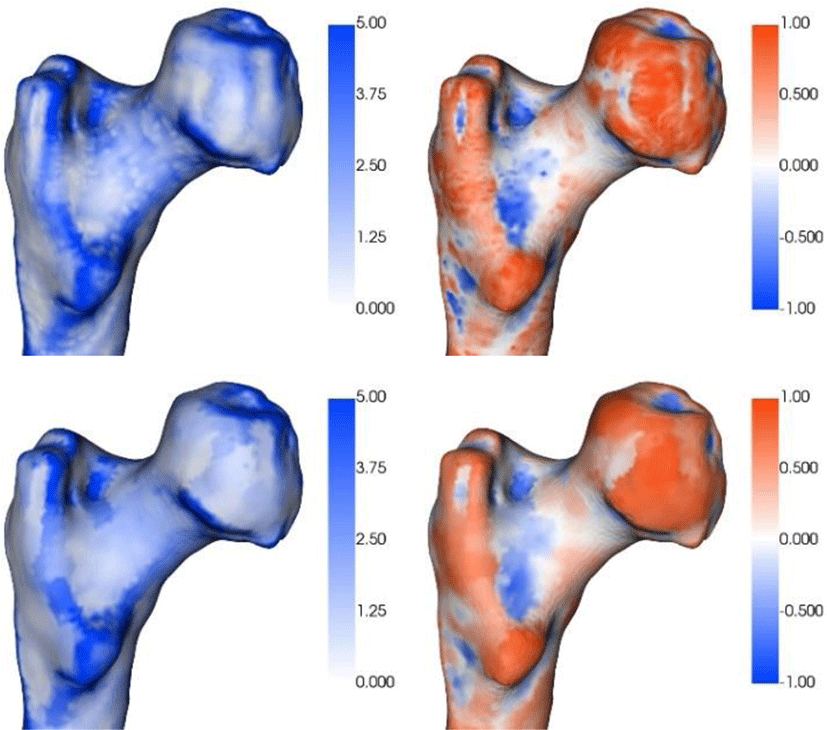
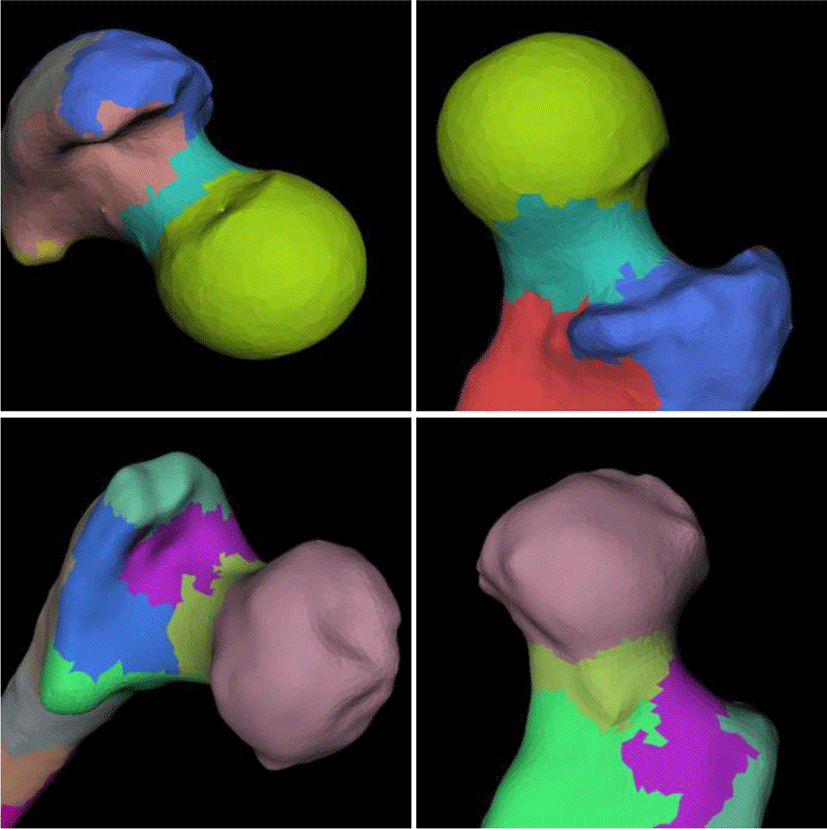
마지막으로, 형태 인덱스와 굴곡도가 비슷한 부분별로 메쉬를 나누기 위해 계층적 면 군집화 [12]를 이용하였다 (Figure 2 참고). 초기에 모든 면은 하나의 군집을 이루며 이웃한 두 군집 간에 수식 (3)과 같은 우선순위 값이 계산이 되고 우선순위 값이 작은 순으로 군집을 병합하였다. 이 때, 면의 형태 인덱스와 굴곡도는 면에 속하는 정점에서 계산된 값의 평균을 사용하였다.
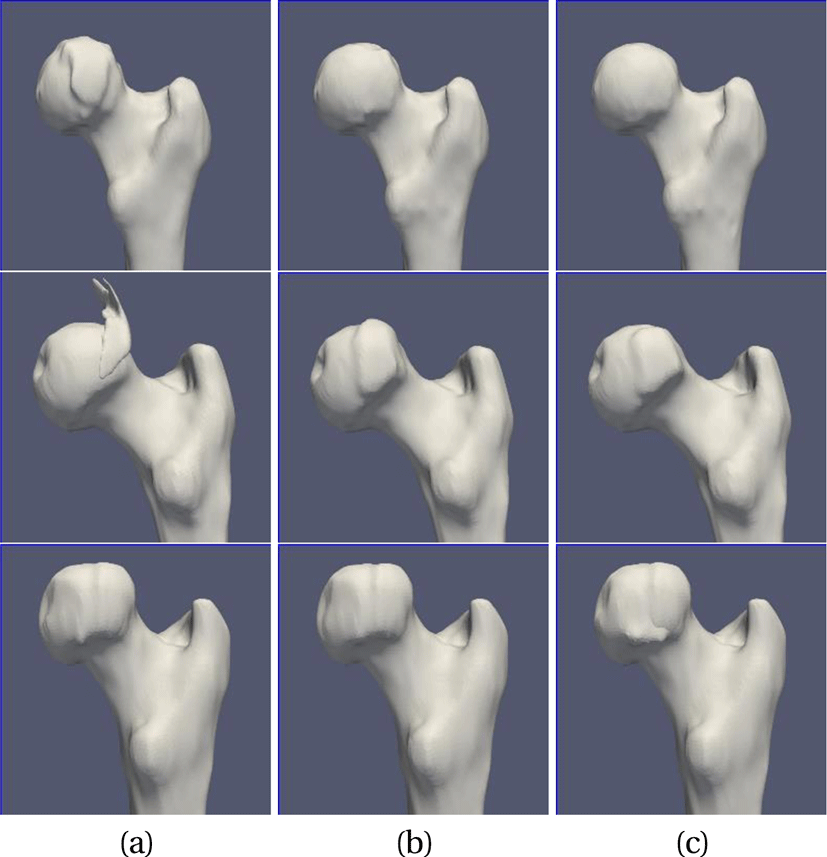
여기서, α1 과 α2 는 각 항에 적용되는 상대적인 가중치이며 si와 ci는 군집 i에 속하는 모든 면의 형태 인덱스와 굴곡도의 평균이다. 그리고, IG 는 군집 G 의 모양 가중치를 나타내며, IG,G′은 G와 G′을 병합한 이후의 모양 가중치를 나타낸다. rG는 군집 G의 경계선의 길이를 나타내며, aG 는 군집 G의 넓이를 나타낸다. 형태 인덱스와 굴곡도만 이용해서 우선순위를 구성하는 경우 군집의 모양과 경계선이 불규칙 해지는 단점이 있다. 군집의 경계선이 불규칙해지면 대퇴골을 의미 있는 단위로 잘 나누기 어렵고 각 부위별로 변형한 후 이들 사이를 연결할 때 연결이 부자연스러워진다. 따라서 우리는 군집을 병합하기 전과 후의 군집의 경계 길이의 차를 수식에 추가했다. 이렇게 하면 군집의 경계길이가 너무 길어지는 것을 방지할 수 있는데, α2 값을 높일 수록 군집의 모양이 점점 원에 가까워진다고 할 수 있겠다. 본 논문의 결과에서는 α1과 α2의 값을 각각 0.7과 1.4로 하였다. Figure 3 은 계층적 면 군집화를 사용하여 대퇴골 메쉬를 여러 부분으로 나눈 결과이다.
5. 메쉬 변형
5장에서는 4장에서 여러 군집으로 분할된 대퇴골 메쉬를 해부학적으로 유의미하게 변형하는 방법에 대하여 설명한다.
현실에 존재하는 대퇴골과 비슷한 데이터를 만들기 위해서 Wang 등 [8]이 소개한 대퇴골의 각 부위의 크기에 관한 확률변수를 사용했다. 각 확률변수들은 대퇴골 특정 부위의 물리적인 측정치와 연관되어 있으므로, 메쉬를 변형할 때 확률 변수를 참고하기 위해서는 메쉬의 물리적 크기를 알아야 한다. 본 논문에서는 원본 CT영상 (DICOM 포맷)에 기록되어 있는 column spacing(mm), row spacing(mm), 그리고 slice thickness(mm) 속성들을 픽셀의 물리적인 크기로 사용하여 메쉬의 물리적인 크기를 계산하였다.
Wange 등[8]이 제시한 확률변수들 중, 4장에서 얻은 군집으로 판별가능한 골두의 반지름 Rfh, 골두와 대퇴골체가 이루는 각 Ans, 내측과 Lm, 외측과 Ll, 그리고 대퇴골체의 길이 Hf 를 사용하여 모델을 변형하였다(Figure 4 참고). 크기가 측정된 부위 (Rfh, Lm, Ll, Hf) 에서는 크기 변환(scaling)을, 각도가 측정된 부위 (Ans) 에서는 회전 변환(rotation)을 적용할 수 있다.
이제부터는 4장에서 얻은 군집들을 이용하여 골두의 반지름 Rfh, 골두와 대퇴골체가 이루는 각 Ans, 내측과 Lm, 외측과 Ll, 그리고 대퇴골체의 길이 Hf 를 구하는 방법을 서술할 것이다. 군집들을 구별하기 위한 절대적인 기준이 없으므로, 모양에 대한 휴리스틱 알고리즘으로 각 군집이 어떤 대퇴골 부위에 해당하는지 판별하였다. 대퇴골은 z축 방향을 따라 길게 놓이므로 대퇴골에서 유의미한 군집을 찾을 때 z축의 좌표를 중요한 지표로 사용하였다. 우선 위쪽의 경계값 thupper 와 아래쪽의 경계값 thlower 두 가지를 정하였다. thupper 와 thlower 는 메쉬 위쪽과 아래쪽으로부터 전체 길이의 25% 만큼 내려가거나 올라온 부분의 z값으로 정하였다. 각 수치는 다음과 같이 계산된다.
-
Rfh: 전체 군집들 중 군집의 중점의 z좌표가 thupper이상인 군집들 중에서 이웃한 군집의 개수가 한 개인 군집(골두)을 찾는다. 그리고 군집의 중점과 정점들 간의 거리를 계산해서 평균값을 Ans로 사용한다.
-
Hf: 군집의 중점의 z 좌표가 thupper 이하, thlower 이상인 군집들의 합집합 S 를 구하고, 이를 한 개의 군집으로 만든다. 그리고 군집 S와 S의 이웃 간의 병합 우선순위가 일정 이하인 동안 계속 병합을 한다. 최종 군집 S의 (최대 Sz - 최소 Sz)를 Hf로 사용한다.
-
Ans: Rfh를 계산할 때 찾은 골두 군집의 중심 (골두 군집에 속해 있는 정점들의 좌표의 평균)과 골두 군집에서 바로 인접해 있는 군집의 중심 쪽으로 향하는 벡터 x 와, Hf에서 가장 처음에 구한 합집합 S 의 정점 집합에 대해서 주성분분석(principal component analysis) [13]을 수행하여 고유값의 크기가 가장 큰 고유벡터 y 를 찾으면, arccos 로 각도를 구할 수 있다.
-
Lm, Ll: 외측과와 내측과가 군집분석에서 완벽하게 분리되지 않는 문제가 있다. 대신, 외측과와 내측과의 앞면은 분할이 잘 된다. 따라서 이 두 개의 군집들로부터 값을 추정할 수 있다. 먼저, thlower 에 있는 군집들 중 형태 인덱스의 평균값이 가장 낮은 군집을 찾는다. 이 군집의 이웃중, 형태 인덱스의 평균값이 가장 큰 두 개의 군집 g1, g2를 찾는다. 그리고 두개의 군집의 중점을 잇는 방향의 벡터와 Rfh 에서 찾은 y 벡터의 외적을 구하여 벡터 z 를 구한다. 그 후, g1, g2 의 중점으로부터 z방향으로 향하는 직선과 메쉬와의 교차점을 구하고, 중점으로부터 교차점까지의 길이를 각각 Lm, Ll로 사용한다.
Wang 등 [8]이 소개한 정규분포를 이용하여 5 개의 대퇴골 부위의 변수들(Rfh, Lm, Ll, Hf, Ans)의 분포로부터 값을 임의로 추출하여 메쉬 변형 시에 사용함으로써 대퇴골의 해부학적 특성을 유지한, 다양한 형태의 메쉬를 생성하였다.
이때, 각 부위의 형태적 특성에 차이가 있으므로 두 가지 메쉬 변형 방법을 사용했다. 먼저, 대퇴골체는 전체적인 길이만 변형하면 충분하므로 자유형상변형기법(free-form deformation, FFD)을 적용하였다 [4]. 대퇴골체를 변형하기 위해서 일정한 간격으로 나눠진 격자들의 기준점들 중, z 축 좌표가 Hf 의 thlower 이상이고 thupper이하인 기준점들 사이의 z축 간격을 정규분포에서 뽑힌 길이로 늘어나도록 늘렸다.
FFD는 구현이 쉽고 변형 방법이 직관적이나 이를 이용하여 메쉬의 구조적 특징과 표면의 국소적 특징을 유지하면서 메쉬를 변형하기는 어렵다. 따라서 나머지 부위에서는 Laplacian deformation [15]을 적용하였다. Laplacian deformation을 사용하기 위해서는 변형이 일어날 부위와 그렇지 않는 부분을 나누는 경계 정점 집합이 필요하다. 이미 대퇴골 메쉬를 부위별로 나누었으므로 군집의 경계 정점들을 이용하여 경계집합을 계산할 수 있다. 경계는 군집의 경계 정점집합에 속한 각 정점의 3-ring neighborhood들의 합집합을 사용하였다. Ans 변형할 때는 골두에 대해서 크기 변환만 적용했고, Rfh 변형하기 위해서 x와y의 외적 z를 구한다음, z를 축으로 하여 골두를 회전하였다. 마지막으로,Lm, Ll 에서 변형해야 할 내측과와 외측과를 정확히 분리하는 것이 불가능하기 때문에, 각각의 앞면의 크기만을 늘렸다.
6. CT 영상 와핑
6장에서는 변형된 대퇴골 메쉬 모델을 기반으로 CT 영상을 와핑하는 방법에 대해서 서술할 것이다.
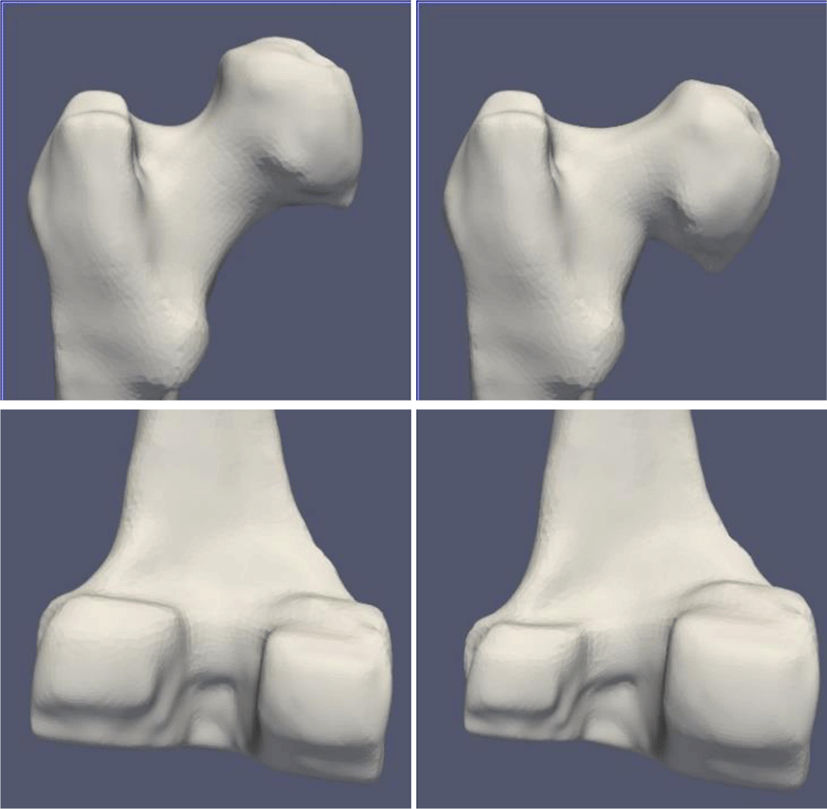
정점의 개수를 보존하면서 대퇴골 메쉬를 변형하였으므로 이동된 정점과 원본 정점을 일대일로 대응하여 원본 정점에 대응되는 CT 영상의 복셀이 변형 후에 얼마나 이동했는지를 나타내는 위치 이동 벡터를 모든 원본 정점에 대하여 계산할 수 있다. CT 영상의 모든 복셀에 대한 이동 벡터를 계산하기 위해 두 모델의 정점 간의 이동 벡터를 전체 CT 영상 영역에 대해 보간한다. 그런 다음, 보간된 벡터들을 이용하여 CT 영상 내의 복셀들을 이동시켜 변형된 모델과 대퇴골 영역이 일치하는 CT 영상을 생성한다(Figure 5).
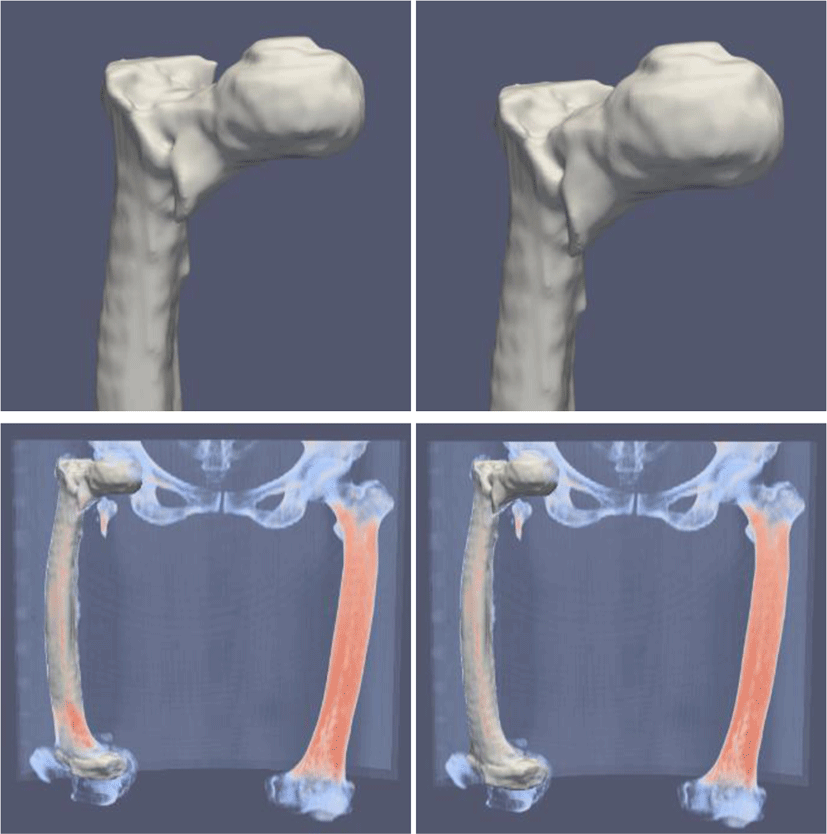
이동 벡터 보간에는 multilevel B-splines을 이용한 근사 방법 [16]을 사용하였다. B-splines을 이용한 데이터 근사는 제어 격자의 해상도가 결과에 큰 영향을 준다. 해상도가 낮은 경우, 데이터의 전체적인 변화 혹은 형태는 잘 근사되나 근사 값과 보간하려는 값 간의 오차가 커지며 해상도가 높은 경우에는 오차는 작지만 데이터 부근에서만 정확한 근사가 이루어지므로 전체적인 변화는 잘 반영되지 않는다. multilevel B-splines을 이용한 방법은 낮은 해상도의 제어 격자로부터 근사를 시작하여 보간하려는 값과 근사된 값 간의 오차를 다음 단계의 높은 해상도의 제어 격자로 근사한 후, 여기서 계산된 근사 값을 낮은 해상도에서 계산된 근사 값에 더 하는 과정을 여러 단계에 걸쳐 반복함으로써 낮은 해상도에서 얻게 되는 전체적인 경향성을 유지하면서 데이터 오차를 줄이는 방법이다.
제어 격자의 해상도가 (l + 3)×(m + 3)×(n + 3) 인 단계에서 계산되는 근사 함수 f(s,t,u) 는 다음 식과 같이 정의된다.
여기서 ϕαβγ 는 (α,β,γ) 에 있는 제어점의 값이며 α=⌊sl⌋−1+p, β=⌊tm⌋−1+q, γ=⌊un⌋−1+r, ŝ=sl-⌊sl⌋, t̂=tm−⌊tm⌋, r̂=un−⌊un⌋ 이다. Bp,Bq,Br 은 균일 삼차 B-spline 기저 함수로 다음과 같이 정의된다.
이때, 0 ≤ λ ≤ 1 이다.
원본 메쉬와 변형된 메쉬의 정점 간의 이동 벡터를 보간할 때, (s,t,u) CT 영상 내의 한 점이며 이동 벡터의 각 좌표값은 f(s,t,u) 에 의해 계산되는 값이다. 이동 벡터는 삼차원 벡터이므로 각 축의 좌표값마다 근사 함수를 계산한다. 본 논문의 실험에 사용된 CT 영상의 해상도는 512 × 512 × 419 이며 이동 벡터 보간 시에는 4 × 4 × 4 해상도의 제어 격자로부터 32 × 32 × 32 해상도의 제어 격자까지 총 4단계로 계산하였다. 이동 벡터 보간을 통해 CT 영상 내의 각 복셀에 대한 이동 벡터를 계산할 수 있으며 이를 이용하여 backward mapping 을 통해 CT 영상을 와핑했다.
7. 실험 결과
아주대학교 병원에서 제공한 한 개의 하반신 CT 영상과 SMIR [17]에서 7개의 전신 CT영상을 실험에 사용하였다. 메쉬를 해부학적으로 유의미하게 변형할 때 대퇴골의 물리적인 크기가 필요하므로 DICOM 포맷의 파일 헤더에 픽셀 간격(pixel spacing)이나 단층 두께(slice thickness)와 같은 픽셀의 물리적인 크기를 계산할 수 있는 정보가 있는지 확인 후에 데이터를 수집하였다. 본 연구에서는 대퇴골 부위만을 사용할 것이므로, 전신 CT영상에서 골반부터 무릎 뼈까지의 영상만을 잘라서 저장하였다.
학습 성능을 향상시키기 위해 몇 가지 영상 전처리를 수행하였다. CT의 HU(Hounsfield Unit) 값을 뼈와 연골 부분만 나타나도록 0에서 2400까지로 절단(clipping)하였고, 연골부분의 대비를 효과적으로 높이기 위해 대비제한 적응 히스토그램 평활화 (contrast limited adaptive histogram equalization) [18]를 적용하였다.
본 연구에서는 영상 분할을 위해 3D U-Net [2]를 사용하였다. U-Net은 크게 두 부분으로 구성되어 있다. 첫 번째는 영상의 특징을 추출하는 인코더(encoder) 부분이다. 그리고 두 번째는 인코더의 마지막 단계에서 추출된 특징 맵(feature map)에 상향 샘플링(up-sampling)을 하고, 이 결과를 인코더의 각 단계에서 추출된 특징 맵과 합치는 것을 반복하여 영상 전체에 대한 분할 결과를 생성해내는 디코더(decoder) 부분이다. 이때, 인코더와 디코더에서 특징 맵을 추출하기 위해 이차원 컨볼루션, 이차원 풀링(pooling), 그리고 이차원 상향 샘플링 연산이 사용된다. 3D U-Net 은 U-Net에서 사용한 이차원 연산들을 삼차원으로 확장하였다. 그리고 딥러닝 모델 학습과정에서 발생하는 여러가지 문제를 완화하는 배치 정규화(batch normalization)를 적용하여 볼륨 데이터(volume data)에 대해서 영상분할 성능을 향상시킨 딥러닝 모델이다.
3D U-Net에서는 모든 연산이 삼차원으로 바뀐 탓에 학습에 걸리는 시간이 기하급수적으로 늘어났다는 단점이 있다. 하지만, 대퇴골의 해부학적 구조가 여러 장의 영상에 걸쳐서 나타나기 때문에 3D U-Net이 이차원 연산 기반의 영상분할 딥러닝 모델보다 본 연구에 더 적합한 방법이라고 생각하여 선택하였다. 그런데, 원본 CT 영상의 크기가 너무 커서3D U-Net으로 학습시키기에는 계산 시간이 너무 오래 소요되므로, x, y, z축 각각에 대하여 4, 4, 4간격으로 하향 샘플링(down-sampling) 하였다.
8개의 데이터 중, 5개를 훈련 데이터(training data set)로, 나머지 세 개를 시험 데이터(test data set)으로 사용하였다. 훈련 데이터로 선택된 5개의 데이터를 기존 방법과 본 논문에서 제안하는 방법을 이용하여 각각 50개씩 증강된 데이터를 만든 뒤, 원본 데이터와 학습 데이터로 사용했다. 영상 분할 성능은 IoU(Intersection over Union) [19]로 측정하였으며 이는 아래와 같이 정의된다.
Table 1에서 볼 수 있듯이, 1, 2번에서는 큰 성능 향상이 없었지만, 영상의 노이즈가 심한 3번 CT에서 큰 성능 향상을 보였다. 또한, 1, 2번 CT에서도 골두와 무릎뼈 부분의 영상분할 결과가 향상된 것을 알 수 있다 (Figure 6 참조).
| CT no. | Proposed (IoU) | Arbitrary (IoU) |
|---|---|---|
| 1 | 0.98 | 0.96 |
| 2 | 0.98 | 0.98 |
| 3 | 0.97 | 0.92 |
8. 결론 및 향후 연구 방향
본 논문에서는CT 영상의 대퇴골 부위를 해부학적으로 의미 있게 변형하여 컨벌루션 신경망(CNN)의 훈련 데이터를 증강하는 방법을 제안하였다. 기존의 방법에 비해 극단적인 성능 향상을 보이지는 않지만, 노이즈가 심한 영상, 그리고 골두와 무릎뼈 주위 등, 경계가 뚜렷하지 않은 부위에서 비교적 좋은 성능을 보였다. 그런데 영상 분할 성능은 높게 측정되지만, 분할된 영역의 경계가 실용적으로 쓰이기에 충분히 깨끗하지 않으므로 향후, 영상 매팅(image matting)을 이용하여 이 문제를 개선해 볼 계획이다. 또한, 데이터 증강 시에 대퇴골 각 부위의 크기만 변형하기보다는, 메쉬 표면에 노이즈를 주거나 모양을 바꾸는 등, 다양한 변형 방법을 이용하여 딥러닝 모델의 일반화(generalization) 성능을 높일 수도 있을 것이다. 마지막으로, 4장에서 대퇴골 메쉬를 의미 있는 부분들로 군집화 할 때 사용되는 우선순위의 각 항의 가중치에 따라 군집화 결과가 극단적으로 달라진다는 문제가 있다. 이 변수들의 조정을 좀더 효과적으로 할 수 있는 방법을 찾아볼 것이다.