1. 서론 및 관련연구
기하학적 물체에 대한 기하 연산의 가속화를 위해 연구되고 있는 다양한 자료구조 중, 복잡한 물체를 간단한 도형의 집합들로 감 싸 계층적 트리 구조를만드는 바운딩 볼륨 계층구조(Bounding Volume Hierarchy, BVH)는 컴퓨터 그래픽스, 애니메이션, 로보 틱스에서 가장 많이 사용되고 있는 자료구조 중 하나이다.
BVH를 사용할 때, BVH를 이루는 요소인 바운딩 볼륨(Bounding Volume, BV)으로 어떤 구조를 쓸 것인지 선택하는 것은 중 요한 문제이다. 구(sphere), 박스 등 간단한 BV는 물체의위치 정 보만으로 만들 수 있어 생성 시간은 빠르지만, 물체를 잘 묘사 하지 못해 근사정밀도가 떨어지는단점이있다. 반면 곡선, 또는 곡면의 기하학적정보를 이용하여 생성한 BV의 생성시간은 느리 지만, 근사정밀도가 높다. BVH는 한번 생성하면 물체의 변형이 있지 않는 이상 재사용이 가능하므로 최근 연구들에서는 간단한 도형으로 빠르게 BVH를 생성하는 것보다 근사정밀도가 높은 도 형을 BV로 채택하여 효율적인 BVH를 설계하는 방향에 초점을 맞추고 있다.
2차원의 경우 자유 곡선에 대한 BVH를 생성하기 위해 가장 단 순한 원으로 BV를 구성하는 것부터 AABB(Axis Aligned Bounding Box), OBB(Oriented Bounding Box)[1], LSS(Line Swept Sphere)[2], RSS(Rectangle Swept Sphere)[3] 등 다양한 BVH가 제안되었다. Meek 등[4] 은 곡률 정보를 활용하여 만든 원호(arc) 를 기반으로 한 평면곡선을 근사하는 방법을 제안하였으며, 이후 Barton 등[5], Kim 등 [6, 7], Lee 등[8]은이를 BVH 생성에 활용 하여 더욱 근사정밀도를 높인 알고리즘을 제안하였다. 원호 기반 접근 방법의 도입으로, 이전까지 완벽한해결이 불가능한 것으로 여겨졌던 고정밀도(108 × 108) 환경에서의 자유 곡선의 오프셋 이나 보로노이 다이어그램 계산 문제들이 해결되었고[9, 10, 11], 최근 연구에서는 BCA Tree[12]로 계산속도와 안정성이 대폭 개 선되었다. 이 결과로 2차원상에서의 자유곡선에 대한 기하 문제 는 더이상 개선의 여지가 없이 완벽하게 해결된 것으로 인식되고 있다.
2차원 문제들에서 효과적으로 사용된 원호 기반 BV를 3차원 기하 문제의 해결을위한 새로운 BV로 아이디어를 확장해보면, 2차원의 원호에 대응되는 3차원의 물체는 토러스이다. 흔히 구면 이라고 생각하기 쉽고, 과거 구면을이용한 BVH 연구가 진행되 었던 적도 있다[13, 14]. 하지만 구면은 자유곡면의 오목한 부분 을 제대로 근사하지 못하며 효율성이 떨어진다. 또한 자유곡면이 볼록하더라도 구면은 모든 방향으로 하나의 고정된 곡률만을 가 지므로 일반적으로 서로 직교하는 두 방향으로 크기가 다른 곡률 을 가지는 자유곡면을 구면으로 정밀하게 근사하기에는 한계가 있다.
이 논문에서는 3차원상의 자유곡면에 대한 효율적인 기하 연 산을 지원하기 위한 새로운 공간자료구조인, 토러스 패치 기반의 정밀 근사를 이용한 자유곡면의 기하학적 처리 기법(이하 토러 스 패치 근사 기법)을 소개한다. 토러스는 곡률이 양이나 음인 경우뿐만 아니라, 0인 부분도 있으므로 곡면의 볼록, 오목 여부 에 영향을 받지 않고 근사할 수 있다. 또한 곡면에서 직교하는 두 방향의 곡률이 서로 다르더라도 토러스의 반지름을 조정하여 곡면을 정밀하게 근사할 수 있다. 이에 대한 근거로, Liu 등[15] 은 3차원상의 임의의 점에서 곡면까지의 수선을 내리는 문제를 해결하기 위해 토러스를 이용하여 곡면을 근사하였다. 이는 Hu 등[16]의 방법에 비해 높은 정밀도를 보장하면서도더 효율적으 로 수선을 구하는 방법으로 알려져 있다.
자유곡면의 법벡터 정보는 컴퓨터 그래픽스에서 렌더링을위 해서 뿐만 아니라, 충돌감지나 거리계산 등의 기하 연산을위해서 필수적으로 요구되는 기하학적정보이다. 법벡터가 필요하지 않 은 계산일지라도 법벡터를 이용하면 불필요한 계산을 수행하지 않아도 되는 경우가 많아, 대부분의 경우 기하 연산의 가속화에 큰 도움을 준다[6]. 주어진 곡면이 가지는 모든 법벡터의 범위를 포함하는 방법으로는 Normal Cone[17], Convex Pyramid[18]등 이 제안되었다.
토러스 패치를 이용하여 자유곡면을 근사하면 위치 정보뿐 만 아니라 법벡터도 거의유사하게 변화하므로 복잡한 자유곡면 의 기하학적정보를 간단하게 표현할 수 있다. 기존의 전통적인 BVH들이위치 정보만 포함할 뿐, 법벡터를 저장하는 경우는 아 주 예외적이므로 이는 토러스 패치 근사 기법의 중요한 장점들 중 하나이다.
오프셋 곡면은 곡면상의 각 점을 곡면의 법벡터 방향으로 일정 한 거리만큼 이동시켰을 때 구해지는 곡면을 말한다. 자유곡면에 대한 오프셋 곡면은일반적으로 입력 곡면보다 훨씬 더 높은 차수 의 대수곡면이 되므로[19], 오프셋 곡면의 근사곡면(일반적으로 오프셋 곡면보다 낮은 차수를 가지는 B-spline 곡면)을 찾는 많은 이전 연구들이 진행되었다[20, 21, 22].
만약 오프셋 곡면이입력 곡면과 동일한 종류의 곡면으로 변환 된다면 별도의 시간을 들여 근사곡면을 계산하지 않아도 되므로 오프셋 곡면을 쉽게 구할 수 있다. 토러스 패치의 경우 토러스를 구성하는 반지름을 조정하는 것으로 오프셋 곡면을 근사하는 토 러스 패치를 추가 연산 없이 곧바로 구할 수 있다. 토러스 이외에 이러한 특징을 가지는 2차원상의 곡선의 예로는 직선, 원 등이 있으며 3차원상의 곡면의 예로는 평면, 구면, cylinder, cone 등이 있다[23, 24, 19].
하우스도르프 거리(Hausdorff distance)는 한 물체에서 다른 물 체까지의 최대 편차를 나타낸다. 하우스도르프 거리가 0에 가까 울수록 두 물체가 서로 유사함을 나타내며, 이런 성질로 두 기하 학적 물체의유사성을 판단하는 도구로 사용된다[25, 26, 27]. 자 유곡선과 자유곡면에 대한하우스도르프 거리 측정에 대한 연구 는 일반적으로 다각형 모델에 대한하우스도르프 거리 측정[25, 28, 29]보다 어려운 문제로 알려져 있다. Kim 등[27]은이중원호 (biarc)를 이용하여 평면곡선의 하우스도르프 거리를 실시간으로 측정하는 방법을 제안하였으며, 자유곡면 간 하우스도르프 거리 를 실시간으로 측정하기 위해 Hanniel 등[30]과 Kirishnamurthy 등[31]은 GPU를 사용하였다. Kim 등[32]은 자유곡면에 BVH를 入}용하여 효과적으로 하우스도르프 거리 후보군을 줄여나가는 방법을 사용하여 자유곡면 간 하우스도르프 거 리를 측정하였다.
토러스 근사기법의 근사정밀도를 측정하기 위하여 한물체에 서 다른 물체로의 하우스도르프 거 리와 그 반대의 하우스도르프 거리 중 최대값인 양방향(two-sided) 하우스도르프 거리를 이용 할 수 있다. 토러스 패치 근사 기법으로 구한 토러스 패치 집합과 자유곡면 간 양방향 하우스도르프 거리의 상한을 Filip 등[33]의 방법을 사용하여 구한 최대근사오차를 이용하여 측정하고, 이 값 이 근사오차한계인 10−6 보다 작음을 보여 토러스 패치 집합이 자유곡면을 정 밀근사함을 입증하였다.
이 논문의 구성은 다음과 같다. 2절에서는 자유곡면에 대한 미 분기하 계산을 이용하여 토러스 패치를 근사하는 알고리즘과 하 이브리드 BVH 구조를 이용하여 토러스 패치의 근사오차를 최소 화하는 방법을 소개한다. 3절에서는 자유곡면 예제와 실험 결과 를 소개하고, 토러스 패치들을 이용하여 두 자유곡면의 교차곡선 과, 오프셋 곡면을 모델링하였다. 4절에서는 이번 연구를 확장하 여 해결할 수 있는 문제들에 대해 소개한다. 마지막으로 5절에서 는 본 연구의 결론을 내린다.
2. 알고리즘
자유곡면 S(u, υ)와 이를 u, υ에 대해 1차 미분한 Su, Sυ 2차 미 분한 Suu, Suυ, Sυυ가 주어졌을 때, 제 1차 기본형식의 값 E, F, G, 단위법선벡터 N, 그리고 제2차 기본형식의 값 L, M, N은 다음과 같이 정의된다.[34].
자유곡면 S(u, υ)의 법곡률 κn은 임의의 방향 υ = aSu + bSυ, a2 + b2 = 1에 대해 다음과같이 정의된다.
여기서 법곡률 κn의 최소값 κ1, 최대값 κ2은 주곡률이 되며, 주 곡률이 될 때의 방향 υ는 주방향 e1과 e2가 된다. 가우스 곡률 (Gaussian curvature) κ는 두 주곡률의 곱으로 정의된다.
자유곡면을 근사하는 토러스 패치를 생성하기 위해 다음 단계를 따른다.
자유곡면을 근사하는 토러스는 Liu 등[15]의 방법을 이용하여 생 성한다. 자유곡면 S(u, υ)와 토러스 근사에 사용할 자유곡면 위 의 점 (u0, υ0)가 주어졌을 때 곡면 위의 점 p = S(u0, υ0), 단 위법선벡터 N, 주곡를 κ1,κ2 그리고 주방향 e1,e2를 구한다. 이 과정을 통해 중심이 p + N/κ1, 축의 방향은 e2, 큰 반지름 R = −1/κ1 + 1/κ2, 작은 반지름 r = 1/ |κ2| 를 가지는, 곡면을 근사하는 토러스를 구할 수 있다.
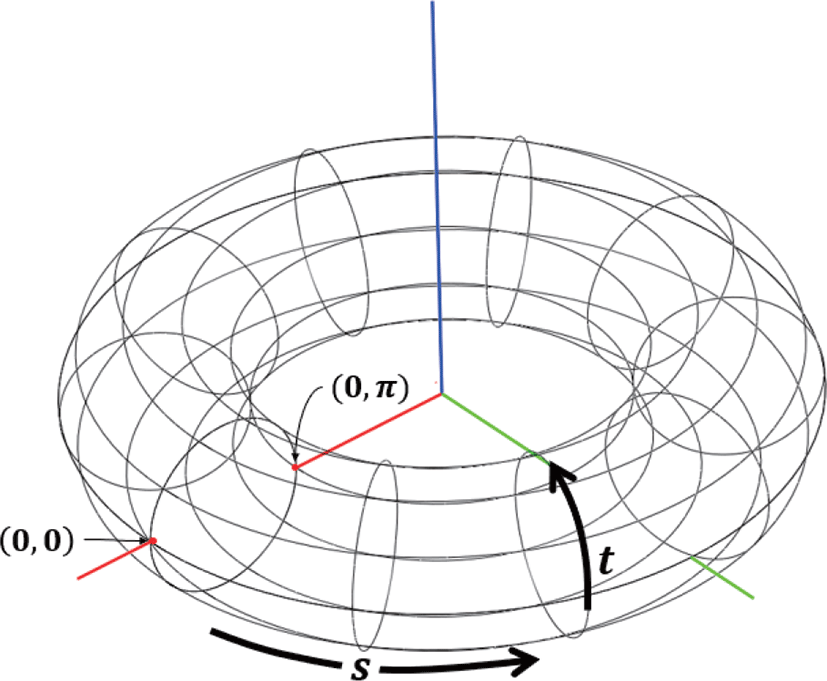
회전축은 Ζ축이고, ΧΥ평면 위 원의 중심점까지의 거리를 큰 반지름 R, 원 중심에서 토러스 곡면까지 거리인 작은 반지름을 r 이라 할 때, 일반적 인 토러스(T̂)의 식은 다음과 같다.
Figure 2은 직교 좌표계와 임의의 반지름 R, r[R > r)에 대한 T̂(s,t)를 나타내고 있다. 회전축의 방향을 (0, 0, 1)에서 e2로 변 환하는 회전행렬 r을 곱하고 중심을 (0, 0, 0)에서 p + N/κ1따로 이동하도록 이동행렬 t을 더하면 S(u0, υ0)의 성분들로 근사한 최종적 인 토러스 T(s,t)를 구할 수 있다.
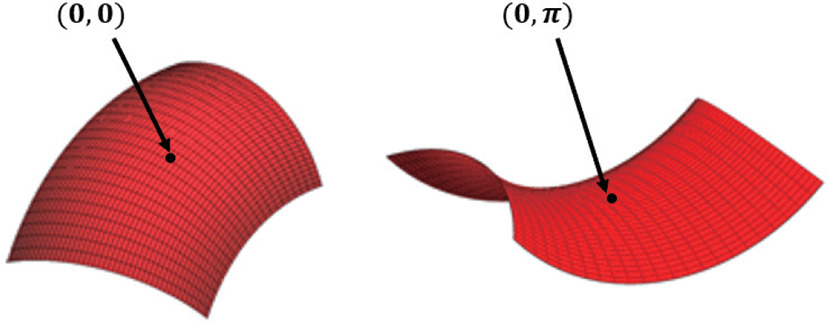
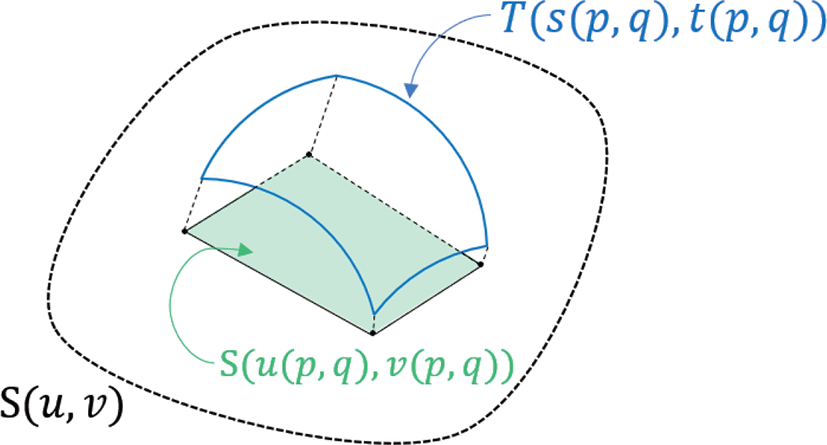
앞서 구한 토러스에서 알고리즘에 사용될 토러스 패치의 영역 을 결정하기 위해 토러스 패치의 중심점과 토러스 패치의 범위를 결정해야 한다. 자유곡면의 S(u0, υ0)에 대응되는 토러스 패치의 중심점 좌표는 (u0, υ0)에서의 가우스곡률 ac에 따라 결정된다. 토 러스의 내부는 가우스 곡률이 음수이고, 토러스의 외부의 가우스 곡률은 양수이다. Figure 3에서 가우스 곡률이 양인 영 역은 붉은 색으로, 음인 영역은 푸른색으로 표시하였다. 따라서 S(u0, υ0) 의 가우스 곡률이 양인 경우, 토러스의 외부(볼록한 면, Figure 6 의 왼쪽 토러스 패치)에 대응되므로 S(u0, υ0)의 토러스 패치의 중심점 좌표 (s,t) = (0,0) 이 된다. 가우스 곡률이 음인 경우, 토러스 내부(오목한 면, Figure 6의 오른쪽 토러스 패치)에 대응 되므로 (s,t) = (0,π)가 된다.

Require: Freeform surface S(u, υ), and point (u0, υ0)
1: R ← −1/κ1 + 1/κ2
:r ← 1/κ2
3: T̂ = MakeGeneralTorus(R, r) ▹ It makes a torus which center is (0,0,0), the axis of rotation is (0,0,1), the major radius is R, and the minor radius is r.
4: c ← S(u0, υ0) + N/κ1
5: r ← Rotation matrix (0,0,1) to e2
6: t ← Translation matrix (0,0,0) to c
7: T = rT̂ + t
토러스 패치는 S(u0, υ0)의 성분들을 이용하여 생성하였으므 로, S(u0, υ0)의 주변 국소적인 부위에서는 토러스 패치가 자유 곡면을잘근사한다. 하지만 S(u0, υ0)에서 멀어질수록 토러스 패 치와자유곡면 사이의 오차는 일반적으로 커진다. 따라서 자유곡 면 전체를 하나의 토러스 패치로 근사하면 근사오차가 커지므로 토러스 패치를 사용하는 장점을 상쇄한다. 따라서 자유곡면을 매 개변수 공간에서 균일한 간격으로 분할하여 자유곡면조각들을 생성하고, 자유곡면조각들을 근사하는 토러스 패치를 생성한다.
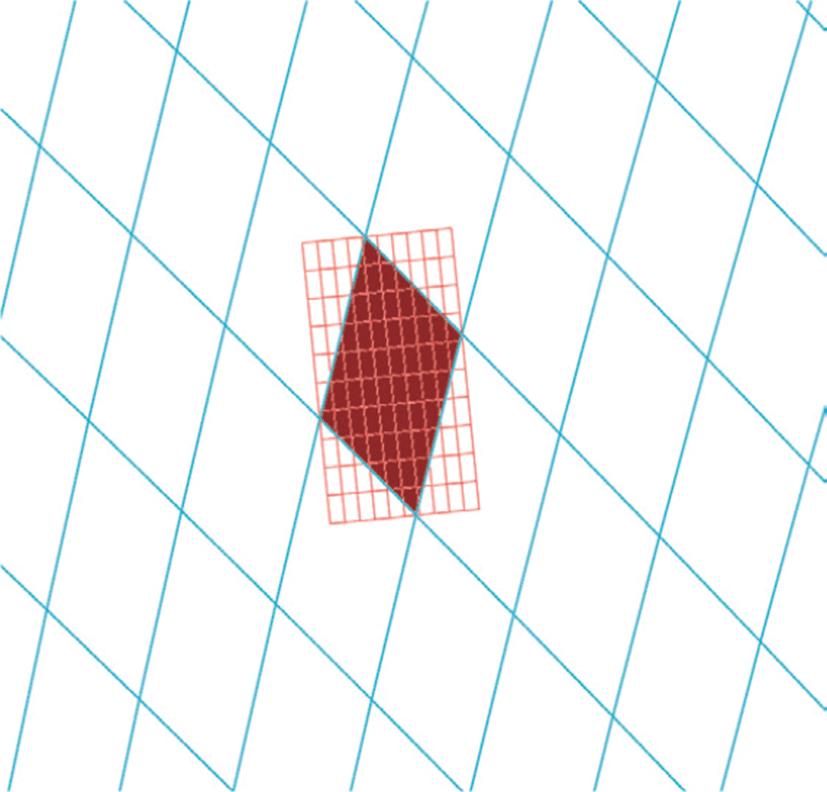
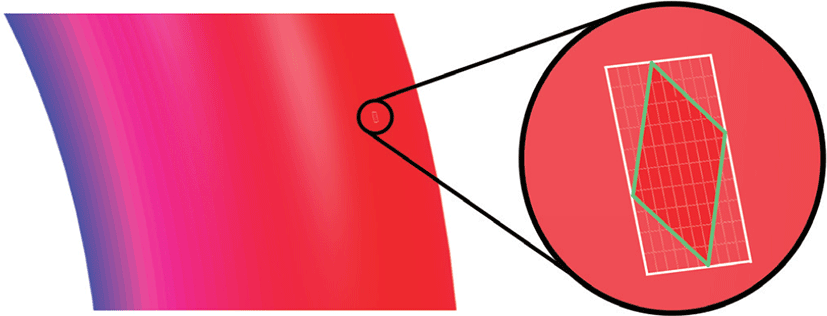
토러스 패치에서 사용하는 범위는 토러스 근사에 이용되는 자유곡면조각의 중심점 (u0, υ0)을 중심으로 자유곡면조각의 위 치정보와 법 벡터정보를 충분히 포함하면서도, 자유곡면조각보 다 지나치게 크지 않도록 조정한다. Figure 4은 자유곡면(파란 색 wireframe)중 자유곡면조각(붉은색 면)의 성분들로 근사한 토 러스 패치(붉은색 wireframe)를 나타낸다. Figure 5는 사용하는 S(u0, υ0)에 따라 생성된 토러스의 일부와 알고리즘에서 사용하 는 토러스 패치(흰색 선)를 나타내고 있다. Figure 4와 Figure 5 에서 보이는 것처럼, 생성되는 토러스의 전체 크기에 비해 실제 알고리즘에 사용하는 토러스 패치의 영 역은 아주 국소적이다.
이 논문에서는 다양한 기하 연산을 지원하기 위한 BVH로서 사 면체 BV와토러스 패치 BV를동시에 사용하는하이브리드 BVH 구조를 사용한다. 앞서 자유곡면을 균일한 간격으로 분할한 자유 곡면 조각을 기준으로, 자유곡면 조각에서 전체 자유곡면까지는 bottom-up 방식으로 사면체[35, 36]를 이용하여 BVH를 생성한 다. 자유곡면조각들은 개별적 인 토러스 패치로 근사시키고, 최대 근사오차가 근사오차한계인 10−6보다 클 경우 그 자유곡면조각 을 매개변수공간 (u, υ), 비에서 각 축으로 이등분하여 4개의 자유곡 면조각으로 분할한다. 분할한 4개의 자유곡면조각들을 다시 토 러스 패치로 근사시키고, top-down 방식으로 이 토러스 패치들이 분할하기 전 토러스 패치와 계층적 구조를 가지게 한다. 이 과정 을 모든 단말(leaf) 토러스 패치의 근사오차가 근사오차한계보다 작아질 때 까지 반복한다.
생성된 토러스 패치들은 자유곡면과 서로 매개변수를 알 수 있 으므로 1:1로 쌍을 이룰 수 있으며, 단말 토러스 패치들로 형성된 토러스 패치 집합은 자유곡면 전체와 대응된다. 자유곡면조각들 의 경계 주위에서는 여러 토러스 패치가마치 물고기의 비늘처럼 겹칠 수 있지만, 자유곡면조각과 토러스 패치가 1:1로 대응되므 로 자유곡면조각 자신에게 대응되는 토러스 패치가 어떤 것인지 쉽게 구분할 수 있다. 더불어 토러스 패치가 겹치는 영역으로 토 러스 패치 간 위치정보를 파악히는데 용이하게 사용할수 있다.
자유곡면을 자유곡면조각으로 분할할 때 큰 간격으로 분할한 다면 BVH에서 사면체 BV들을 사용하는 단계가 적어지고, 최상 위 단계의 토러스 패치 BV들의 근사오차가 커진다. 작은 간격으 로 분할한다면 사면체 BV들을 사용하는 단계가 많아지고, 최상 위 단계의 토러스 패치 BV들의 근사오차가 작아져 토러스 패치 BV들의 단계가 적어진다. 따라서 임의의 자유곡면이 주어졌을 때 자유곡면조각으로 분할하는 간격의 크기는 자유곡면의 차수, 허용오차의 크기, 그리고 하이브리드 BVH가 기하 연산을 해결하 는데 소요되는 시간등을 고려하여 실험적으로 결정하여야한다.
Require: Freeform surface S
1: Divide S to S00, S01,…,Smn
2: Build hierarchical structure by tetrahedron BV ▹Bottom-up
3: Stack.push(S00, S01,…,Smn)
4: while !Stack. emptydo
5: Sij = Stack.top
6: Stack.pop
7: Tij = TorusPatchApproximation(Sij)
8: ifGetError (Sij, Tij) > ε then ▹ ε : tolerance
9: Divide Sij to Sij00, Sij01, Sij10, Sij11
10: Build hierarchical structure ▹ Top-down
11: Stack.push(Sij00, Sij01, Sij10, Sij11)
12: end if
13: end while
토러스 패치 집합과 자유곡면 사이의 양방향 하우스도르프 거 리 의 상한을 구하기 위해 이들의 최대근사오차를 먼저 계산할 필요 가 있다. 이를 위해 토러스 패치가근사하는 자유곡면상의 영 역과 토러스 패치 사이의 오차를 모두 측정하고, 그 최대값을 구한다. 생성한 토러스 T(s, t)중 앞서 설정한 토러스 패치에 따라 토러스 의 국소 범위만 사용하므로, 토러스 패치의 이용 범위를 (p,q) ∈ [0,1] × [0,1]로 재매개화하여 T(s, t) = T(s(p, q), t(p, q))로 표현 하고, 이 영 역을 자유곡면에 투영시킨 영역을 S(u(p, q), υ(p, q)) 로 표현한다. Figure 7의 파란색 T(s(p, q), t(p, q))는 토러스 패치 룰, 초록색 영역은 토러스 패치를 자유곡면 S(u, υ)에 투영시킨 영 역 S(u(p, q), υ(p, q))을 나타낸다. 이때, (p,q)로 재매개화된 토 러스 패치는 토러스의 전체 영역에 비해 매우 국소적이므로, 계 산의 편의성을 위해 (p,q)와 (u,υ)사이의 관계는 아핀변환으로 가정한다. p,q에서 u,υ로 가는 아핀 변환이 다음과 같을 때
이를 p,q에 대해 편미분 한 결과는 아래와 같다.
이를 미분의 연쇄법칙을 이용하여 일차미분, 이차미분으로 확장 시켜 p,q 에 대한 미분값들을 u,υ 에 대한 미분값으로 표현할 수 있다.
토러스 패치를 n2개의 아주 작은 이중선형곡면으로 분할한 뒤, 앞서 구한 미분값들을 이용하여 Filip 등[33]의 방법에 따라 최대 근사오차를 측정할 수 있다.
토러스 패치 집합상의 임의의 점에서 자유곡면까지의 최단거 리는 항상 최대근사오차보다 작거나 같다. 반대로, 자유곡면상의 임의의 점에서 토러스 패치 집합까지의 최단거리도 항상 최대근 사오차보다 작거나 같다. 따라서 토러스 패치 집합을 구성하는 각각의 토러스 패치와자유곡면 사이의 양방향吞1우스도르프 거 리 상한은항상 그들의 최대근사오차보다 작거나 같다. 또한토러 스 패치의 최대근사오차가 10−6 이상일 경우 자유곡면을 추가로 분할하여 계층적 구조를 가지게 하는 2.2절의 알고리즘에 따라, 양방향 하우스도르프거 리 의 상한은 항상 10−6보다 작음이 보장 된다.
토러스 패치 근사 기법을 사용하면 자유곡면의 오프셋 곡면을 쉽 게 구할수 있다. 이는 토러스의 오프셋 곡면이 오목, 또는 볼록의 형태는그대로유지되면서 곡률의 크기만 달라지기 때문이다. 앞 서 구한 토러스에서 작은 반지름에 오프셋 값을 더한 값을 r0이라 할 때, 토러스의 오프셋 곡면 T0(s, t)는 다음과 같이 정의된다.
오프셋 곡면의 회전행렬 r과 이동행렬 t는 입력 곡면의 회전행 렬, 이동행렬과 동일한 행렬이다. 이런 토러스의 성질로, 오프셋 한 토러스 패치 집합과 오프셋한 자유곡면간의 양방향 하우스도 르프 거리의 상한은 입력 곡면과 토러스 패치 집합과의 양방향 하우스도르프 거리의 상한과 같아오프셋한 토러스 패치 집합의 최대근사오차를 쉽게 계산할 수 있는 토러스 패치 근사 기법의 장점을 확인할 수 있다.
3. 실험결과
토러스 패치 근사기법의 근사정밀도를측정하기 위해 세개의자 유곡면 S(u,v)에서 u,v 각방향으로 128개씩 나누고 하이브리드 BVH 구조를 생성하였다. Figure 9의 예제 1, 2는 3차 베지어 곡 면이며 예계 3은 2차 베지어 곡면이다. 문제의 크기를 동일하게 하기 위해 베지어 곡면의 제어점을 감씨는 바운딩 박스의 대각선 길이가 1이 되도록 조정하였다. 각 예제의 제어점은 다음과 같다.
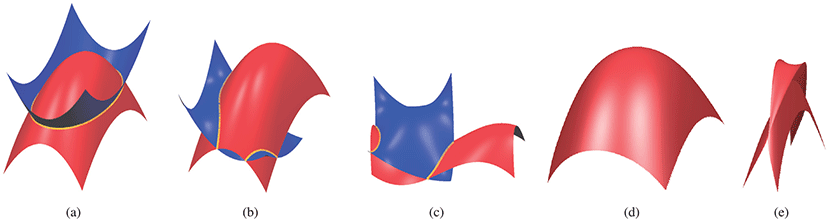
세 개의 자유곡면 각각에 대해 토러스 패치 집합을 이용하여 모 델링하였다. Figure 9는 3개의 예제 자유곡면과 토러스 패치 집 합으로 감싼 모습을 나타낸다. 토러스 패치들의 구별을 위해, 각 토러스 패치들이 임의의 색으로 렌더링 되도록 하였다. Figure 9(a)는 주곡률이 양인 자.유곡면이며, Figure 9(b)-(c)는 주곡률이 양과 음인 지점을 모두 포함하는 자유곡면이다. 토러스 패치가 자유곡면의 볼록, 오목 여부에 영향을 받지 않고 자유곡면을 잘 근사힘을 확인할 수 있다.
Table 1에서는 각 只ᅵ유곡면과 토러스 패치 집합에 대해 최대 근사오치 를 측정하였다. 3개의 자유곡면 모두 최대근사오차가 10−6보다 작으므로, 자유곡면과 토러스 패치 집합간의 양방향 하우스도르프 거리가 10−6보다 작음을 알 수 있다.
| 최대근사오차 | 최대 | 평균 | 최소 |
|---|---|---|---|
| 예제 1 | 5.792−9 | 4.797−9 | 2.667−9 |
| 예제 2 | 1.501−8 | 4.411−9 | 4.168−10 |
| 예제 3 | 5.536−9 | 2.605−9 | 1.734−10 |
Figure 8에서는 토러스 패치 근사 기 법을 이용한 기하 연산을 수행한 예제를 제시하였다. Figure 8(a)는 예제 1 곡면(붉은색)과 이를 뒤집은 곡면(푸른색)을, Figure 8(b)는 예계 1 곡면과 예제 3 곡면을, Figure 8(c)는 예제 2 곡면과 예제 3 곡면을 서로 교차 하게 만들고 토러스 패치만을 이용하여 교차곡선(노란색)을 계 산한 결과이다. 토러스 패치 내부에서 교차곡선 점들의 추적을 위해 marching method와 subdivision method[37, 38]를 활용하였 다. 교차곡선상의 점들은 두 자유곡면과의 거리가 10−6 이하이 다. Figure 8(d)-(e)는 예제 1 자유곡면을 토러스 패치 근사 기법으 로 토러스 패치 집합을 생성 한 후 각각 0.15, -0.15씩 오프셋 한 결과이다. 아직 자기 교차(self-intersection)곡선는 제거하지 않은 상태의 예제이다.
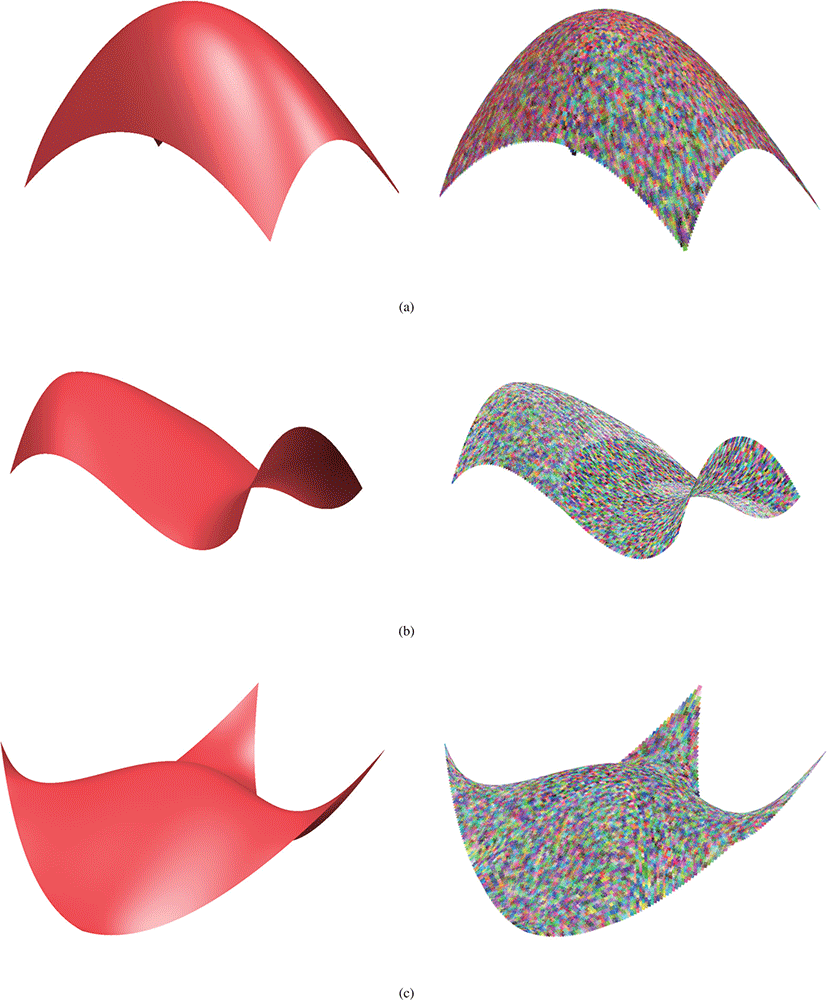
4. 확장가능한주제들
토러스 패치 근사 기 법을 이용하여 두 자유곡면의 교차곡선을 계 산하였다. 향후 자유곡면에 속하는 토러스 패치간의 상관관계를 파악하고, 토러스간 교차곡선을 계산하는 이전 연구들[39, 40]을 확장할 수 있다. 이를 통해 더욱 정밀한 두 자유곡면의 교차곡 선을 계산하고, 접하는 곡면들 사이의 교차곡선 계산 등 수치적 으로 대단히 불안정한 경우의 문제들을 해결할 수 있을 것으로 기대된다.
오프셋 곡면에서는 자기교차를 제거하는 것이 중요한 문제로 남아있다. 입력 곡면에서 곡률이 높은부분은오프셋 크기가 커짐 에 따라 국부적으로 꼬이는 오프셋 곡면을 생성하므로 자기교차 가 일어난다. 이런 자가교차점이 발생하는 (u, v)의 집합이 아주 복잡한 위상을 가지기 때문에, 기존의 그리드 기반 접근 방법으 로는 해상도의 문제로 인하여 정밀도가 높게 문제를 해결하는 데 한계가 있었다. 이 문제에 토러스 패치 근사 기 법을 활용한다면, 고정밀도의 계산을 효율적이고 안정적으로 수행할 수 있을 것이 다. 이를 응용하여 오프셋 크기를 변수로 고려하여, 오프셋 곡면 들로 구성되는 3차원 볼륨 모델링으로 결과를 확장할 수 있다.
3차원 물체에 대한 보로노이 다이 어그램(Voronoi Diagram)이 나 중심축(Medial Axis) 계산을 하기 위해서는 서로 마주 보는 두 곡면 사이의 중간위치에 있는 이등분(Bisector) 곡면 계산을 정확 하게 해야 한다. 이 곡면은 그 차수가 매우 높을 뿐만 아니 라 근사 오차를측정하기 어려워 안정적인 알고리즘의 개발이 어려웠다. 이를 근사정밀도가 높은 토러스 패치 근사기법을 사용하여 접근 한다면 거 리계산 문제의 기하학적 인 근사오차를 분석하는 데 큰 장점 이 있을 것으로 예상된다.
최근 3차원 모델링에서 중요한 연구 주제가 된 사각 메시에서 사각형의 방향은 주방향을 따라가도록 생성되는 경우가 일반적 이다. 하지만 곡면을 근사하는 사각 메시는 근사 과정 에서 법벡터 정보가 부정확해진다. 또한 사각 메시를 이루는 면인 쌍선형곡면 (bilinear surface)은 항상 곡률이 음이므로, 자유곡면 중 곡률이 양인 부분을 표현하는데 한계가 있다. 이를 토러스 패치 근사 기 법으로 접근한다면 향후 사각 메시에 대해서도 법벡터 정보를 유지하면서 매우 높은 근사정밀도를 가질 것으로 예상한다. 이를 통하여 자유곡면과 사각 메시 사이에 적용되는 다양한 알고리즘 개발에 중요한 역할을 할 것으로 기대된다.