1. 서론
광선 추적법(Ray Tracing)은 빛의 물리적인 성질을 고려하여 사실감 있는 3차원 렌더링을 구현하는 장면 가시화 기법으로, 사용자 시점에서 가상의 3차원 장면을 향해 많은 광선을 발생시키고 광선의 경로를 추적하여 스크린의 픽셀 색을 정한다. 광선은장면을 순회하면서 물체의음영을 표현하고(Shading), 물체에 의해 차단되며(Shadow), 한 물체에서 다른 물체로 반사되고(Reflection), 투명 또는 불투명한 물체를 통과하며 굴절(Refraction) 된다. 광선추적법에서는 이러한 모든 상호작용을 결합하여 최종 스크린 픽셀 색을 결정한다 [1].
근래 들어 광선 추적 계산 가속을위한 RTX GPU 플랫폼이 소 개되었는데 이는 장면을 구성하는 기하 자료 구조의 구축 및 탐색을 가속화하고, 기계 학습 기반의 디노이징 기법과 함께 새로운 렌더링 파이프 라인을 제공하여 실시간 광선 추적법이 가능한 응용 프로그램을 개발할 수 있게 한다 [2].
점집합(Point Set)은 메쉬에 비해 위상 정보가 요구되지 않는 개념적 단순성을 이점으로 가진다. 또 세밀한 서피스를 표현하기 위해서 많은 수의 작은 프리미티브들이 요구되는데 점집합은 이를 모델링하고 렌더링하기에도 적절한 기하 표현이라고 볼 수 있다 [3] [4]. 한편, 무작위적인 점 프리미티브로 구성된 점집합 모델을 GPU로 렌더링하기 위해서 연속 표면으로 근사할 필요가 있다 [5]. 광선 추적법에서 이 표면과 광선의 교차 검사 및 교차 지점에서의 쉐이딩 효과를 계산함으로써 사실감 있는 장면을 렌더링할 수 있다 [6].
Figure 8b은 점집합을 사용한 댜앙한 응용 기술들의 예를 보여 준다. 최근들어 급격하게 늘어난 3차원 환경 스캐너의 발전으로 물리적 환경을 더 정확하게 점집합으로 표현하고자하는 요구가 늘어났고 특히 SLAM(Simultaneous Localization and Mapping) 및 자율 주행 기술의 발전으로 도심 환경과 같은 거대환경을 스캔하여 획득한 점집합을 최대한 실사에 가깝게 가시화하는 요구 역시 증대되고 있다(Figure 1a). 또한 물리적으로 다른 공간에 있는 사용자들을 한공간에 있는 것처럼 느낄 수 있게 구현한 원 격현실(Telepresence)에서는 타지의 사람을 스캔한 점집합을 현실감 있게 렌더링하고 합성하여 사용자의 몰입감을 높여 준다 (Figure 1b). 그리고 사람이나 동물 등의 생명체를 여러 대의 스캐너로 스캔하여 획득한 점집합을 렌더링하여 아바타로 표현하거 나, 유적지를 렌더링한 결과를 홀로그램으로 보여주어 몰입형혼 합현실 어플리케이션에 활용할 수도 있다(Figure 1c). Autodesk사의 Recap, Bently사의 Pointtools와 같은 점집합프로세싱 소프트웨어는 점집합으로 인식된 실제 환경을 현실에 가깝게 3차원 가상 환경으로 시뮬레이션하고 그 결과는 측량, 도시, 건설 등의 분야에서 다양하게 활용되고 있다.

본 연구에서는 이런 점집합에 대한사실적 렌더링 요구를바탕으로 점집합에 대하여 광선 추적 법 전용 GPU와 랜더링 파이프 라인을 적용한 실시간 전역 조명(Real-time Global Illumination) 랜더링을 수행하여 실제 객체나 환경을 현실감 있게 시각적인 시뮬레이션을 구현하고자 한다. 본 논문에서는 점집합으로부터 매끄러운 다양체 표면을 표현하기 위해 미분 기하학 기반의 이동 최소 자승법 (MLS)을 사용하여 표면을 음함수(Implicit Surface) 로 근사한 후, 이에 광선 추적법을 적용하여 전역 조명 효과를 표현한 실시간 랜더링 기법을 제안한다.
한편, 광선 추적법의 실시간 구현을 위하여 RTX GPU 플랫폼 상의 DXR 라이브러리에서 제공하는 광선 추적법 전용 렌더링 파이프라인을 이용한다 [10]. 하지만 RTX GPU 플랫폼은 삼각형 프리미티브로 구성된 장면에 대해서만 광선 추적법을 지원하는 한계가 있기 때문에 본 연구에서는 점 프리미티브로 구성된 점집합을 사용하여 표현한 장면에 대하여 실시간 광선 추적법을 가능 하게 하도록 플랫폼 기능을 확장하였다. 그 결과 점집합 모델이 포함된 장면에 대해 효과적으로 광선 추적법이 수행되어 실시간 전역 조명 렌더링이 가능하도록 하였다.
2. 관련 연구
Levoy와 Whitted [11]가 프리미티브로서의 점집합의 가능성에 대해 소개한 이후 점집합을 렌더링하기 위한 수많은 그래픽스 연구가 진행되어 왔다 [12]. 연결성이 없는 점집합으로 표면을 렌더링하기 위한 실용적인 기법도 제안되었다 [3] [13].
이동 최소 자승법(Moving Least Squares)은 점집합으로 표면을 재건하는 주요 기법 중 하나이다. 이 기법은 정렬되지 않은 점집합으로부터 메쉬를 생성할 수 있게 한다 [14]. Levin [15]은 분포된 점집합을 매끄러운 표면으로 근사하기 위해 이동 최소 자승법의 최적화에 기반한 투영 연산자를 도입했다. 이 투영 기법을 사용하여 Alexa et al. [5]은 점집합의 표면 렌더링에 대한 고품질 알고리즘을 제시하였다.
점집합 광선 추적법을위해 Adamson과 Alexa [16]는 점집합으 로부터 표면을 근사하기 위해 이동 최소 자승법을 기반으로 하되 간소화된 기법을 소개하고 이에 광선 추적법을 적용하였다. 이 논문에서 제시된 접근법에 용의한 구현 방법을 바탕으로 Wald 와 Seidel [17]은 최적화를 접목한 실시간 점집합 광선 추적법 모델을 연구했으며 그 결과 백만개의 점집합으로 구성된 모델에 대해 전처리된 전역 조명 렌더링을 수행했을 때 400×600 해상 도에서 4FPS정도의 성능을 보였다. 본 연구의 예비 초록판 [18] 에서는 그래픽스 하드웨어를 이용한 전역 조명 렌더링을 제안 하였고, 640×640 해상도에서 3만 6천개의 점짐합 모델에 대해 69FPS의 성능을 보였다.
광선 추적법은 계산량이 많은 기법이기 때문에 성능 향상을 위해 하드웨어의 지원이 요구된다. 이에 따라 NVIDIA사는 2018년 광선 추적법 전용 하드웨어를 출시하였다. 이 하드웨어에는 70 개 정도의 광선 추적법을위한 RT Core가 장착되어 있다. 기존에는 광선 한 개당 Bounding Volume Hierarchy(BVH)내의 바운딩 박스(Bounding Box)와의 교차 검사를 거쳐 박스 내 삼각형과의 최종 교차 검사를 위해 수천개의 소프트웨어 명령어가 수행되었다. 반면 RTX 그래픽스 하드웨어에 장착된 RT Core는 두개의 유닛으로 구성 되어 있으며, 한 유닛은 BVH 순회 및 광선-바운딩 박스 교차 검사를 처리하고 다른 유닛은 광선-삼각형 교차 검사를 처리한다. 그 결과 기존에 비해 초당 처리할 수 있는 광선의 수가 약 10배 이상 증가하였다 [19].
한편, RTX의 광선 추적법 기능이 통합된 광선 추적법 렌더링 파이프라인인 DirectX의 DXR API를 통해 전역 조명 응용 프로그램을 개발할 수 있다. DXR에서는 광선과 기하와의 효율적인 교차 계산을 위해 기하들을 하위/상위 가속단계(Bottom/Top Level Acceleration Structure)로 나누어 관리한다. 하위 가속단계에서는 삼각형, Axis-Aligned Bounding Box(AABB)등의 기하프리미티 브들이 포함되고, 상위 가속단계에는 변환 행렬과 재질(Material) 등이 포함된다. 또한 개별적 광선에 대하여 새로운 쉐이더들이 순차적으로 수행되는데, 먼저 광선 생성 쉐이더(Ray Generation Shader)에서 광선을 생성하면 장면을 구성하는 BVH를 순회하며 광선과 바운딩 볼륨과의 교차를 검사한다. 그리고 교차된 바운딩 볼륨 내 기하 객체들과의 교차 검사를 위해 연결된 힛그룹(Hit Group)의 쉐이더들이 수행된다. 교차 쉐이더(Intersection Shader) 는 광선과 기하의 교차점을 찾고 그 지점의 쉐이딩 계산은 최근 접교차 쉐이더(Closesthit Shader)에서 수행되는 방식이다. 또한 광선과 기하와의 교차가 발생하지 않는다면 비교차 쉐이더(Miss Shader)가 수행된다 [2].
3. RTX 기반 점집합의 전역 조명 렌더링
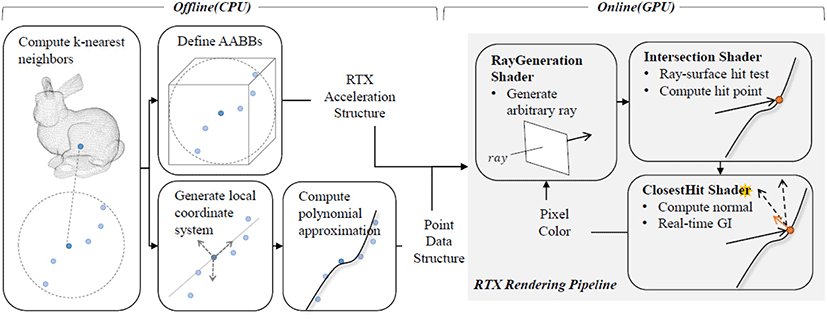
점집합에 대한 전역 조명 렌더링을 수행하기 위해서는 근사된 연속 표면이 필요하고 이 표면에 광선 추적법을 적용해야 한다. Figure 2는 점집합에 대한 전역 조명 렌더링을 수행하는 전체 프 로세스를 보여준다. 먼저 오프라인으로 각 점의 k-최근접 이웃들 및 이를 포함하는 AABB 정보와 접공간 지역 좌표계로의 변환에 필요한행렬, 음함수를 정의하는다항함수의 계수를 선계산하고, 이를 각 점의자료구조에 저장한다. 그리고 온라인으로 점의자료 구조를 사용하여 실시간 광선 추적법을 수행하여 최종 픽셀 색을 결정한다.
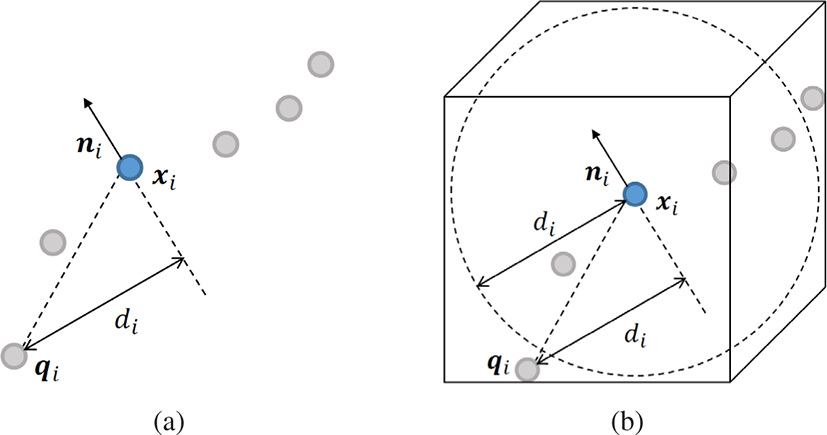
각 점 xi가 영향을 미치는 영역을 정의하기 위해 k-최근접 이 웃들을 구한다. 중심이 xi이고 반지름 di를 가진 구 안에 최대 9 개의 최근접 이웃들이 포함되도록 한다. Figure 3a와 같이 점을 품는 최대의 지역을 정의하기 위해 점 xi와 최근접 이웃점들 중 최장 거리에 있는 점 qi로 구성되는 방향 벡터를 구하고 이 방향 벡터를 점 xi의 법선 벡터 방향에 대해 투영한 길이를 이용하여 di를 구한다 [20]. 그리고 Figure 3b와 같이 di를 반지름으로 하는 구를 포함하는 AABB를 정의한다.
광선 추적법에서는 각 광선마다 BVH를 순회하며 바운딩 박스와 의 교차여부를 검사하고 가장 가깝게 교차된 바운딩 박스를 찾 는다. RTX는 이 과정을 RT Core 하드웨어를 기반으로 하여 가속 화하고 있으며, 장면을 구성하는 AABB를 RTX에서 다루는 가속 구조로 구축하도록 요구하며 이 가속 구조를 빌드하고 업데이트 하는 과정을 최적화하고 있다 [21].
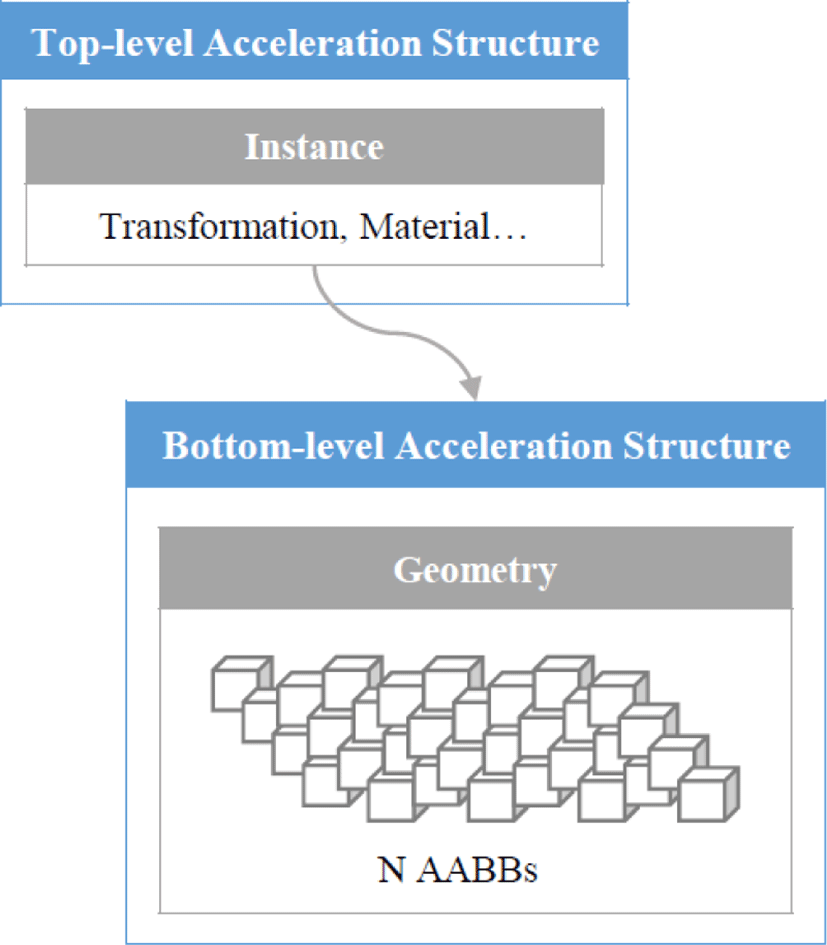
이에 따라 Figure 4와 같이 하위 단계가속 구조는 3.2절에서 정의한 각 점에 대한 AABB의 집합으로 구성하였고, 모든 AABB들을 한 개의 기하 구조에 포함시켰다. 상위 단계가속 구조는 하위 단계 구조를 참조하며 변환 행렬과 재질 정보 등을 저장하도록 구성하였다.
점집합을 연속적인 음함수 표면으로 근사하기 위해 Figure 5a와 같이 먼저 각 점의 위치와 법선 벡터로 참조평면을 정의하고 이 평면에 이웃 점들을 직교 투영한다. 투영된 점들로부터 접공간을 생성하여 점 xi를 원점으로 하는 접공간 지역 좌표계를 구성한다.
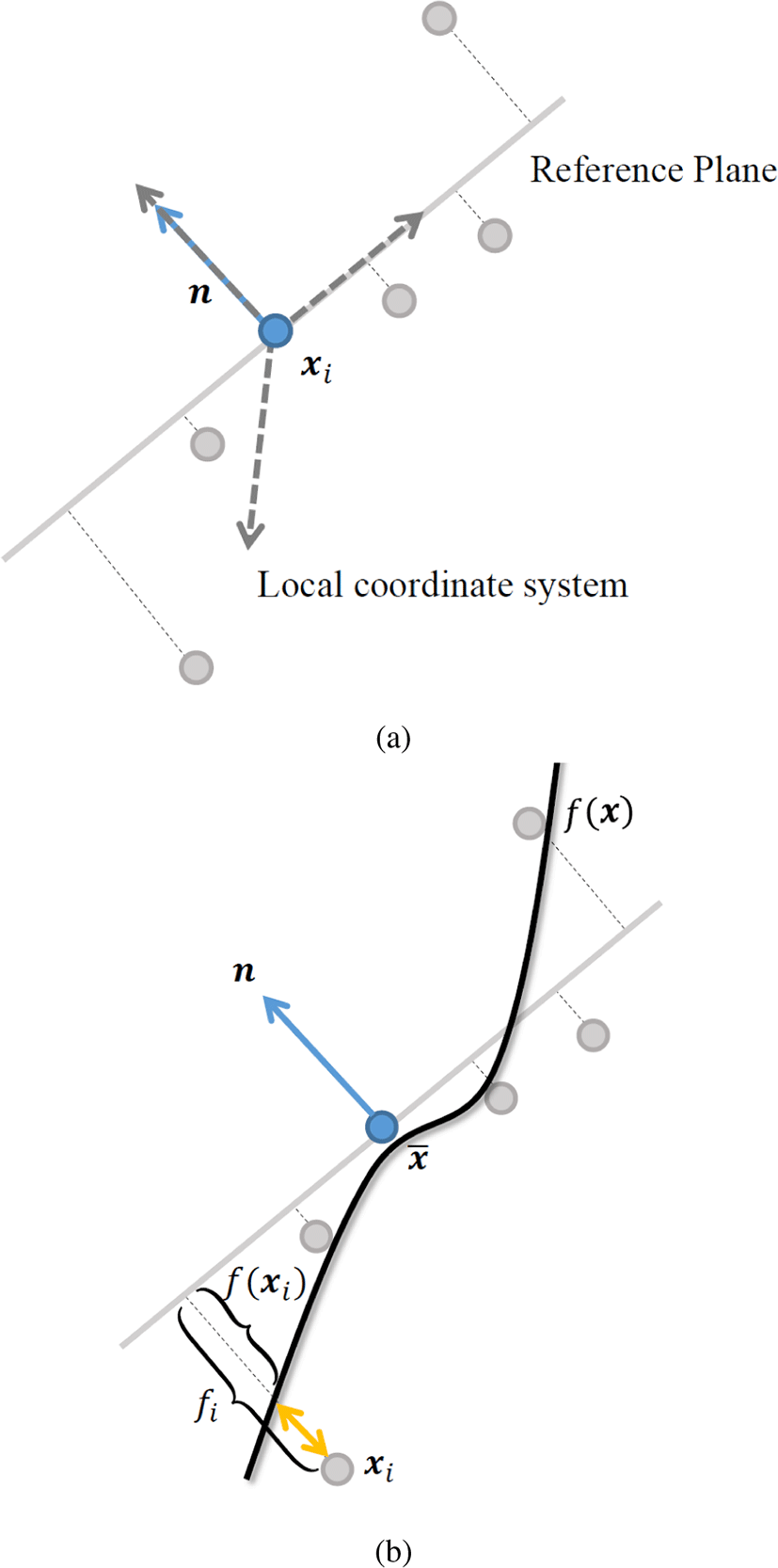
Figure 5b와 같이 점집합으로 표면을 근사하기 위해 이동 최소 자승법에서는 보편적으로 지역 좌표계 안에서의 이차 다항함수 f(x) = b(x)T c 를 정의한다. b(x) = [1, x,y,x2, xy, y2]T는 다 항함수 기저 벡터이고 c = [c1, c2, c3, c4, c5, c6]T 는 다항함수 계수 이다. 이 다항함수의 계수를 계산하기 위해, 이동 최소 자승법을 적용하여 이웃점을 참조평면으로 직교 투영했을 때 평면까지의 거리와 투영점에서 근사된 표면까지 거리의 차를 최소로 만족하도록 한다. 이 최소화 문제는 다음의 식으로 계산한다.
또한 각 점에서부터 이웃까지의 거리에 대한 가중치를 고려하기 위해서 Wendland 함수를 가중치 함수로 적용한다.
그 결과 각 점에 대하여 접공간으로의 변환 행렬과 다항함수의 계수를 점의자료구조에 오프라인으로 저장하고, 온라인 광선 추적법 계산시에 사용한다.
RTX는 삼각형 프리미티브에 대한 교차 쉐이더를 내장하여 광선-삼각형에 대한 교차 검사를 지원하고 있지만 점 프리미티브에 대해서는 지원하지 않기 때문에 사용자가 교차 쉐이더를 필요에 따라 구현하여야 한다. 이를 위해 사용자는 점기하에 대해서 바운딩 박스를 정의하고 RTX 가속 구조에 적합하게 이를 저장한 후, 광선과 바운딩 박스가 교차했을때 호출되는 교차 쉐이더 안에서 광선과 바운딩 박스내 실제 점기하 모델과의 교차 여부를 판별한다.
이와 같은 RTX의 렌더링 파이프라인에 따라, 렌더링 과정이 온라인으로 시작되면 Figure 6a와 같이 먼저 하드웨어의 지원으로 가속화된 BVH 순회의 결과로 광선의 방향에 대한 최근접 AABB가 찾아진다. 그리고 그 AABB에연결해 놓은 힛그룹의 교차 쉐이더가 호출되어 광선과 음함수 표면과의 실제 교차 검사를 수행하게 된다.
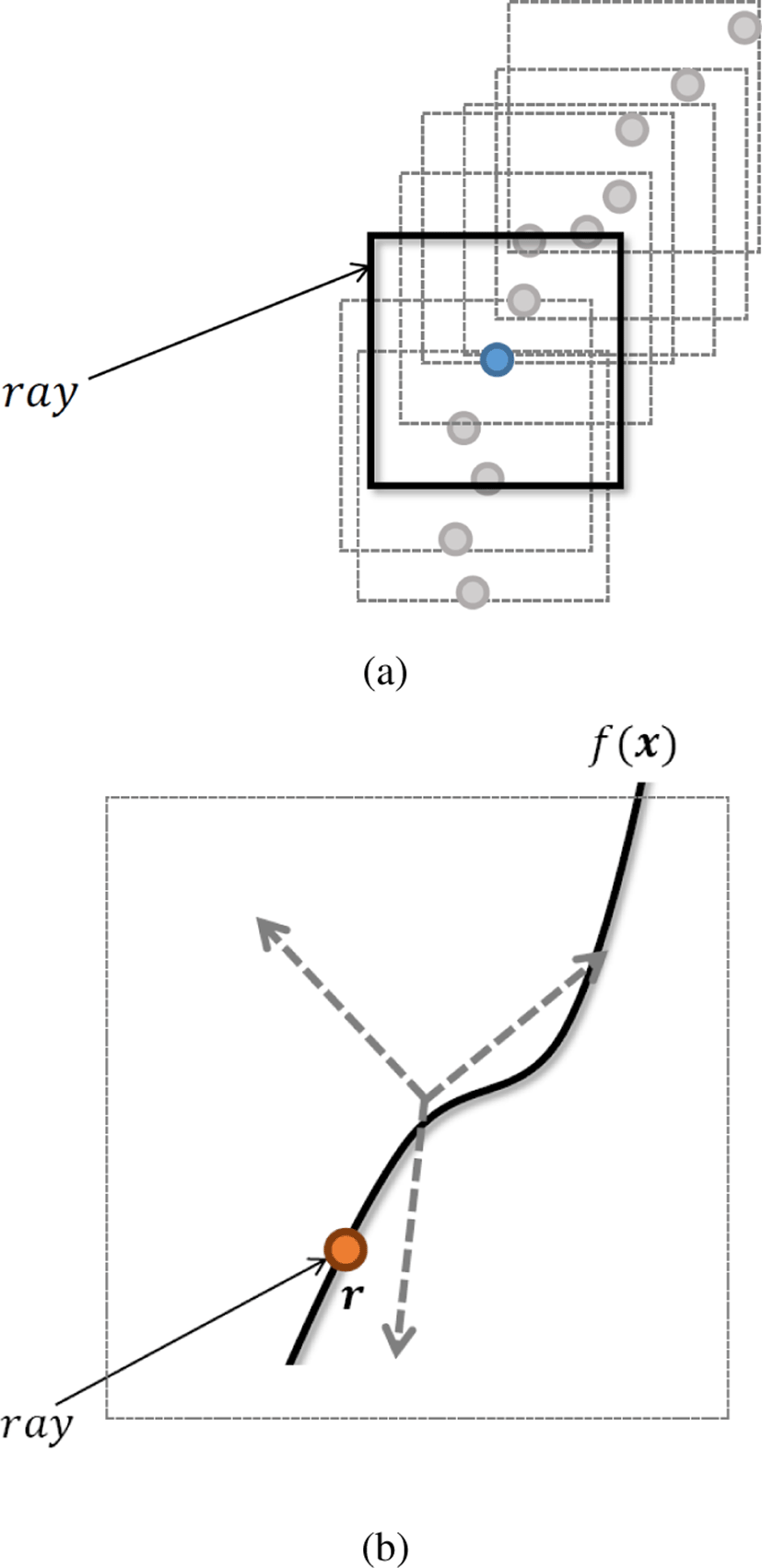
이때 점의자료구조에 저장되어 있던 접공간 변환 행렬을 사용 하여 광선을 지역 좌표계로 변환한 후 표면을 근사한 지역 다항함 수와 광선의 교차점을 찾는다. Figure 6b와 같이 광선상의 임의의 점 r, 시작점 o, 방향벡터 d, 이동거리 t를 가지는 광선 r = o + td 를 다항함수 f(x)에 대입하여 광선의이동거리 t에 대한 이차 방정식 f(r) = 0을유도한다.
이차 방정식의 유효한 해 t를 찾았다면 해당하는 광선상의 점을 계산하고 그 점이 AABB 안에 포함되고 또 시작점에서부터 가장 가까운 점인지 확인하여 t를 선택함으로서 최종 교차점이 결정된다. 만약 그렇지 않다면 광선과 표면은 교차하지 않는 것이므로 다시 BVH를 순회하고 다음으로 가까운 AABB가 찾아지면 AABB에 연결된 교차 쉐이더가 호출되어 동일한 교차여부 검사가 진행되며 최종 교차점이 결정될 때까지 이를 반복 수행하게 된다.
교차점이 결정되면 힛그룹의 최근접교차 쉐이더를 실행하여 쉐이딩 효과를 계산한다. 쉐이딩 효과를 계산하기 위해서는 교차점에서의 법선 벡터가 필요하기 때문에 교차점에서의 음함수 표면의 기울기 벡터를 계산한다. 단 법선 벡터의 방향에 따라 표면이 전면인지 후면인지 구별되게 되는데, 광선과의 교차점이 발생한 음함수 표면은 전면이라고 정하여 법선 벡터를 정의하도록 한다. 이를 위해 광선의 방향 벡터와 기울기 벡터의 사잇각이 예 각이라면 기울기 벡터로 인해 음함수 표면이 후면으로 인식되지 않도록 기울기 벡터의 방향을 반대 방향으로 바꿔주고 이를 법선 벡터로 저장하여 교차점이 발생한 음함수 표면을 전면으로 정의 한다.
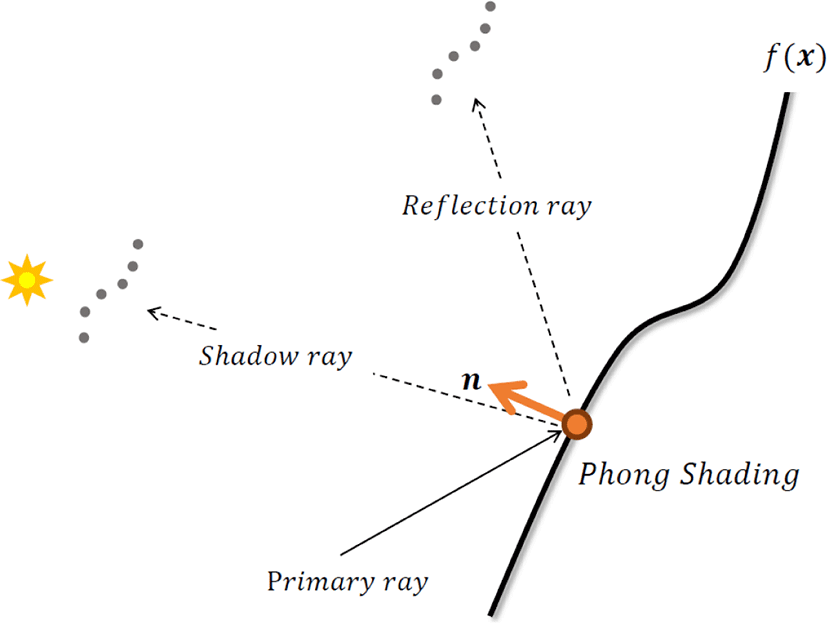
Figure 7과 같이 지역 좌표계 상에 놓여 있던 교차점의 위치를 전역 좌표계상 위치로 변환하고 앞서 정의한 법선 벡터를 사용하여앰비언트(Ambient), 디퓨즈(Diffuse), 스페큘러(Specular) 요소를 표현하는 퐁 쉐이딩(Phong Shading)을 계산한다. 그리고 전역 조명을위하여 교차점에서 2차 광선을 발생시킨다. 또한 그림자 효과를 위해 교차점에서 광원을 향한 2차 광선을 발생시키 고, 그림자 광선과 점집합 모델과의 교차가 발생한다면 그림자 광선을 발생시킨 지점에 그림자 색을 반영한다. 또한 반사 효과를 위해 교차점으로 들어온 입사 광선에 대한 반사 광선을 2차 광선으로 발생시켜 점집합 모델과의 교차가 이루어 지면 해당 교차점의 색을 반사색으로 반영하여 최종 픽셀의 색을 결정한다. 하지만만약 정의된 최대 길이의 광선에 대해서도 점집합의음함 수 표면과의 교차점이 결정되지 않는다면 광선과 점집합 모델은 교차하지 않는 것이므로 비교차 쉐이더가 호출되며 해당 광선에 대해 배경색을 반영한다.
4. 구현 및 결과
본 연구는 64bit 윈도우즈 10 운영체제과 마이크로소프트 비주얼 스튜디오 2017 C++에서 구현되었고, 모든 렌더링은 AMD사의 Ryzen 7 3700X CPU, NVIDIA사의 RTX 2080 GPU, 16GB RAM 이 설치된 환경에서 수행되었다.
렌더링 대상인 점집합 모델은 삼각형 모델으로부터의 연결 정보를 제외하고 점의 위치 정보만으로 구성된다(Figure 8b). PCL [22]을 사용하여 계산한 각 점의 법선 벡터와 최대 9개의 k-최근접 이웃들로부터 점의 AABB 크기를 계산하였다.
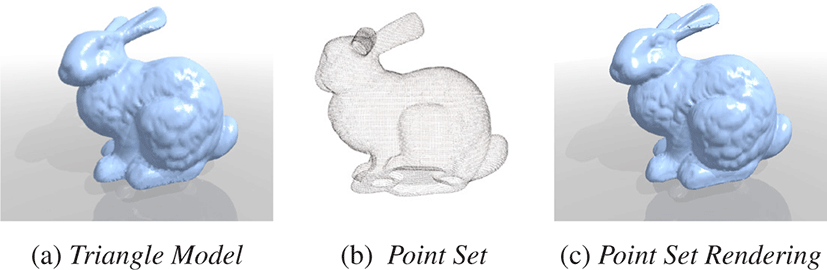
광선 추적법 렌더링을 수행하기 위해 DirectX의 DXR을 사용 하였다. Figure 8은 640×640 해상도를 가진 스크린에 전역 조명 렌더링을 수행한 결과이다. 3만 6천개의 점으로 구성된 점집합 모델을 전역 조명 렌더링 한 결과 1,000FPS 이상의 실시간 렌더링 속도를 보였다. 광선 추적 깊이는 2단계로 하여 그림자와 반사 효과를 처리하였다.
Figure 9는 640×640 해상도 스크린에서 여러 점집합 모델들에 대해 그림자와 반사 효과를 위한 2단계 전역 조명 렌더링을 수 행한 결과이다. 장면은 삼각형 프리미티브로 구성된 바닥 모델과 점 프리미티브로 구성된 점집합 모델로 구성되어 있으며, RTX의 하위 단계 가속 구조는 한개의 기하 종류만 포함할 수 있으므로 각 모델에 대한 하위 단계 가속 구조를 정의하고 이를 참조하는 각각의 상위 단계가속 구조 및 힛그룹을 정의하였다. 이 가속 구 조는 삼각형 모델 및 점집합 모델이 동시에 포함된 장면과 광선의 교차 검사를 가능하게 하였다. 점집합 모델은 부드러운 음함수 표면으로 렌더링 되었고 또한 각 점마다 k-최근접 이웃들을 고 려하여 AABB의 크기를 정의했으며 AABB 안에 음함수 표면이 포함되도록 하여 점집합 렌더링시 발생하는 빈 간격(Hole) 문제를 최소화하였다.

광선 추적법을 적용한 전역 조명 렌더링의 성능을 평가하기 위해 해상도별 렌더링 속도를 측정하였다. Table 1은 640×640 해상 도와 1858×1057 해상도에서 각각 점집합 모델들에 대한 렌더링을 수행했을 경우 성능을 측정한 결과를 보여준다. 50만개의 점집합으로 구성된 모델의 경우 640×640 해상도에서 60FPS 이상, 1858×1057 해상도에서 40FPS 이상의 성능을 보였다. 광선 추적은 픽셀 단위로 발생되는데 해상도가 확대됨에 따라 추적 횟수가 증가하며 이로 인한 계산량의 증가는 FPS의 감소로 나타남에도 불구하고 실시간 전역 조명 렌더링이 수행되는 것을 확인하였다.
| Models | # of points | FPS | |
|---|---|---|---|
| 640×640 pixels | 1858×1057 pixels | ||
| Bunny | 35,947 | 1,000 | 676 |
| Horse | 48,485 | 927 | 650 |
| Armadillo | 172,974 | 133 | 113 |
| Dragon | 437,645 | 84 | 65 |
| Buddha | 543,652 | 62 | 46 |
또한 기존의 연구 [17]가 600×400 해상도에서 백만개의 점집 합 모델에 대해 전처리된 전역 조명 렌더링을 수행했을 때 4FPS 정도의 성능을 보였던 것과 비교하여 본 연구 결과에서는 백십만개 정도의 점집합 모델에 대한 전역 조명 렌더링(Figure 9d)을 동일 해상도에서 수행하였을 때 45FPS의 빠른 성능을 보였다.
한편, 점집합 모델의 실시간 렌더링 성능 향상을 위해 최적화 작업을 수행하였다. RTX 하위 단계 가속 구조는 RTX 기하 자료 구조에 AABB들을 저장하여 이 기하 자료구조를 여러개 생성할 수 있는 방식이다. 본 연구에서는 최적의 RTX 하위 가속 구조 를 찾기 위해 다양한 실험을 시도하여, 한개의 AABB를 포함한 RTX 기하 자료구조를 정의하고 이 기하 자료구조를 점의 갯수 만큼 생성한 것 보다 한개의 RTX 기하 자료구조를 정의하고 그 안에 점의 갯수만큼의 AABB들을 포함시킨 것이 약 3.3배 정도 높은 성능 결과를 보임을 확인하였다.
또한 렌더링 파이프 라인을 따라 호출되는 쉐이더내 계산에 필요한 점의자료구조에는 점의위치, 접공간 지역 좌표계로의 변환 행렬, 음함수의 다항함수 계수, 재질 정보가 포함되어야 한다. 이는 CPU에서 계산되고 DirectX의 구조 버퍼(Structured Buffer)에 저장되며 GPU가 접근하여 사용한다. 이때 GPU가 접근하는 빈도에 따라 버퍼내 자료를 분리하여 각각의 버퍼로 관리함으로써 성능을 향상시킬 수 있다 [23]. 예를들어, 교차점의 쉐이딩 계산 을위해한번만 호출되는 최근접교차 쉐이더에서 사용되는 재질 자료를 별도의 구조 버퍼로 분리한다. 그리고 교차점을 찾을 때까지 재귀적으로 호출되는 교차 쉐이더에서 사용하는 재질외 점의 자료들을 또다른 구조 버퍼로 구성하였다. 이렇게 GPU가 접근하는 빈도에 따라 점에 대한 자료들을 여러 구조 버퍼로 분리한 결과 한개의 구조 버퍼에 점의 자료들을 관리한 것에 비하여 FPS 가 2배 정도 증가하는 것을 확인하였다.
5. 결론 및 향후 연구
본 연구에서는 RTX GPU 플랫폼에서 지원하는 광선 추적법을 위한 가속 엔진을 기반으로 점집합에 대해 전역 조명기반의 실시간 렌더링 기법을 제안하였다. RTX가 제공하는 기본적 프리미티브가 아닌 점집합을 위해 이를 부드러운 음함수 표면으로 근사하고 광선과의 교차 검사를 수행하였다. 또한 점집합 기하가 포함된 장면에 2차 광선을 통해 그림자와 반사 효과를 반영하여 사실감 있는 이미지를 실시간으로 생성하였다.
하지만 점들의 분포가 일정하지 않은 점집합인 경우 음함수 표면이 부드럽게 근사되지 않는 문제가 발생하며 또한 서로 이웃한 음함수 표면의 연결성에 따라 경계 부분이 드러나는 현상은 현재 연구의 한계점으로 남아있다.
추후 대용량의 점집합에 대한 실시간 전역 조명 렌더링을 수행 하기 위해서 외부 메모리(out-of-core memory) 관리 및 효율적인 자료 구조를 사용하고자한다. 또한 최근접 AABB 검출 후 광선과 기하와의 교차 검사와 그에 따른 쉐이딩 효과계산시에 광선과 음함수 표면의 교차 검사 계산 처리를 향상시킬 수 있는 연구를 진행 할 예정이다. 마지막으로 음함수 표면의 곡률 및 최소 탐색 범위에 따라 k-최근접 이웃들의 개수를 정의하여 AABB 크기를 최적화하고 인접한 음함수 표면의 연속성을 보장하여 보다 부드러운 다양체로렌더링이 가능한 연구를 진행할 예정이다.