Journal of the Korea Computer Graphics Society

The Korea Computer Graphics Society

J Korea Comput Graph Soc 2021; 27(4):11-24

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2021.27.4.11

Article

노이즈가 완화된 거품 효과를 표현하기 위한 인공신경망 기반의 투영맵 정제

김종현¹^,^*

Refinement of Projection Map Based on Artificial Neural Networks to Represent Noise-Reduced Foam Effects

Jong-Hyun Kim¹^,^*

¹강남대학교

¹Kangnam University

^*corresponding author: Jong-Hyun Kim/Kangnam University(jonghyunkim@kangnam.ac.kr)

© Copyright 2021 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 01, 2021; Revised: Aug 02, 2021; Accepted: Aug 27, 2021

Published Online: Aug 31, 2021

요약

본 논문에서는 액체 시뮬레이션에서 표현되는 거품 효과(Foam effects)를 노이즈 없이 디테일하게 표현할 수 있는 인 공신경망 프레임워크를 제안한다. 거품 입자의 생성 위치와 이류는 기존의 스크린 투영법을 활용하여 계산되며, 이 과정에서 나타나는 노이즈 문제를 인공신경망을 통해 풀어낸다. 스크린 투영 접근법에서 중요한 것은 투영맵이지만 이산화된 스크린 공간에 운동량을 투영하는 과정에서 투영맵에 노이즈가 발생하며, 우리는 인공신경망 기반의 디노 이징(Denoising) 네트워크를 활용하여 이 문제를 효율적으로 풀어낸다. 투영맵을 통해 거품 생성 영역이 선별되면 2D 를 3D 공간으로 역변환하여 거품 입자를 생성한다. 우리는 작은 크기의 거품들이 소실되는 기존의 디노이징 네트워크 문제를 해결하였다. 뿐만 아니라, 제안하는 알고리즘을 스크린 공간 투영 프레임워크와 통합함으로써 이 접근법이 갖는 모든 장점을 그대로 수용할 수 있다. 결과적으로 깔끔한 거품 효과 뿐만 아니라, 디노이징 과정으로 인해 소실된 거품을 안정적으로 표현할 수 있는지 다양한 실험을 통해 보여준다.

Abstract

In this paper, we propose an artificial neural network framework that can represent the foam effects expressed in liquid simulation in detail without noise. The position and advection of foam particles are calculated using the existing screen projection method, and the noise problem that appears in this process is solved through an proposed artificial neural network. The important thing in the screen projection approach is the projection map, but noise occurs in the projection map in the process of projecting momentum into the discretized screen space, and we efficiently solve this problem by using an artificial neural network-based denoising network. When the foam generating area is selected through the projection map, 2D is inversely transformed into 3D space to generate foam particles. We solve the existing denoising network problem in which small-scaled foam particles disappear. In addition, by integrating the proposed algorithm with the screen-space projection framework, all the advantages of this approach can be accommodated. As a result, it shows through various experiments whether it is possible to stably represent not only the clean foam effects but also the foam particles lost due to the denoising process.

Keywords: 유체 시뮬레이션; 거품 효과; 디노이징; 인공신경망; 투영맵

Keywords: Fluid simulations; Foam effects; Denoising; Artificial neural networks; Projection map

1. 서론

물리 기반 유체 시뮬레이션은 물 [1, 2], 불 [3, 4, 5], 연기 [6, 7, 8], 불똥 [9, 10, 11], 거품 [12, 13], 버블 [14, 15], 미스트 [16, 17] 등 다양한 시각적 특수효과를 풀어내기 위해 사용되었다. 그 중에서 물은 출렁이는 움직임에 따라 거품, 버블, 스플래쉬 같 은 부차적인 효과가 나타나는 대표적인 재질이며, 이러한 특 징을 효율적으로 풀어내기 위해 다양한 접근법들이 제안되었 다 [18, 19]. 일반적으로 기본 유체의 유동을 분석하여 스플래 쉬, 버블, 거품 등을 표현하며, 각 재질에 따라 다른 이류 방 식을 채용하여 움직임을 제어한다. 하지만, 이러한 접근법은 3D 유체의 움직임으로부터 추출되기 때문에 계산양이 크며, 이를 효율적으로 계산하기 위한 다양한 스크린 공간 투영 접 근법들이 제안되었다 [20, 21]. 이 접근법은 실시간으로 거품 효과를 표현하기 위해 깊이맵과 노멀맵을 이용하였지만, 2D 공간만을 이용하기 때문에 3D 공간에서 표현되는 거품이나 스플래쉬를 정확하게 표현하기에는 한계가 있다. 특히 거품 의 이류를 표현하지 못하기 때문에 이질감이 눈에 띄게 나타 난다. 이와 같은 이유로 스크린 투영 접근법은 대부분 게임과 같은 실시간 애플리케이션에만 적용되었다.

최근에 Kim 등은 2D와 3D 공간을 모두 사용하여 거품의 효 율성과 품질을 개선시켰다 [22, 23]. Figure 1에서 보듯이 3D 유 체의 움직임을 2D 스크린 공간에 투영하여 거품이 생성될 후 보군을 찾은 뒤, 다시 3D 공간으로 역변환하여 거품을 생성한 다. 결과적으로 2D 공간만을 사용했을 때 나타나는 이질감을 줄였고, 3D 공간상에서 거품을이류(Advection)시키기 때문에 사실적인 거품의 움직임을 표현했다. 하지만 입자의 움직임 을 2D 공간으로 투영하는 과정에서 에일리어싱(Aliasing) 문제 가 발생하며, 이러한 문제는 거품의 품질에도 영향을 미친다. Figure 2는 2개의 박스들이 회전하면서 생성되는 거품 결과이 며, 그때 생성되는 가속도맵을 시각화 한 것이다. 그림에서도 보듯이 2D 공간에 투영된 맵은 빠르고 느린 입자들이 혼합되 면서 경계부근에에일리어싱 문제가 발생하며, 이러한 문제를 해결하기 위해 분리 가능한 이항필터(Separable binomial filter) 를 사용하기도 하지만 거품이 소실되는 문제가 발생한다.

Figure 1: Illustration of inverse-transformation of 2D foam-sourcing triangle into 3D space [, ].

Download Original Figure

Figure 2: An aliasing problem that occurred in the process of projecting 3D particles into 2D space (red : faster accelerating).

Download Original Figure

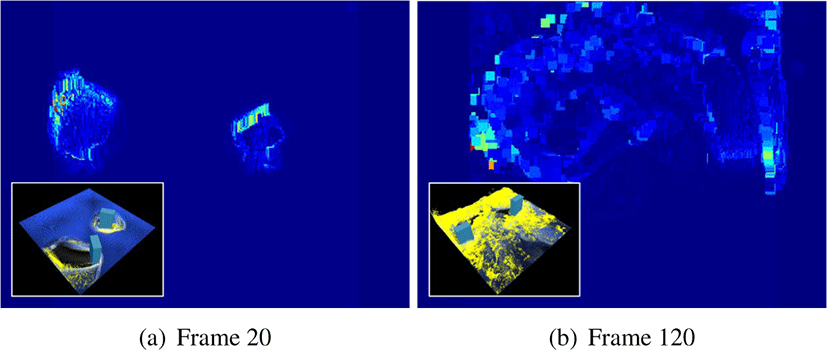
투영맵에 나타나는 노이즈 문제는 거품의 생성에도 큰 영 향을 준다 (Figure 3a 참조). 특히, 유체 입자들이 소싱되는 영 역이나, 스플래쉬처럼 공기중으로 튄 입자들이 물 표면에 빠 른속도로 충돌되었을 때 노이즈한 거품 뿐만 아니라 연속된 프레임에서 깜빡거리는 문제가 발생하기도 한다. 이 문제를 해결하기 위해 이항필터를 적용하게되면 노이즈한 거품은 제 거되지만, 거품 입자들도 소실되는 문제가 심각하게 발생한다 (Figure 3b 참조).

Figure 3: The filtering technique used in the previous methods [, ] (red box : noise area).

Download Original Figure

본 논문에서는 인공신경망 기반의 투영맵 정제 기술을 제안 하여 소실 없이 거품을 표현할 수 있는 프레임워크를 제안한 다. 제안하는 기법을 구현하기 위해서는 입력 유체의 움직임 으로부터 다음과같은 하위 문제를 풀어야 한다:

투영맵 데이터 수집. 투영맵을 학습시키기 위한 데이터를 수집하는 과정이며, 본 논문에서는 Kim 등의 기법을 [22, 23] 이용하여 입자들의 움직임을 2D 공간으로 투영한 후, 분리 가능한 이항 필터를 통해 정제 후의 투영맵 데이터 를 수집한다.
노이즈 제거를 위한 인공신경망 설계. 잔차(Residual) 보정 기반의 ConvNet(Convolutional Neural Networks, CNN) 을이용하여 노이즈 제거 네트워크를 모델링한다.
인공신경망을 활용한 통합형 거품 프레임워크. 노이즈가 제거된 투영맵을 기존의 거품 생성 프레임워크에 새롭게 통합하는 방법을 제안한다.

첫번째 문제를 해결하면 네트워크를 학습하기 위해필요한 데이터가 수집된다. 이 과정은 거품 손실없이 투영맵을 정제 하기 위한 데이터 구성 단계로써 매우 중요한 과정이다. 두번 째 문제를 해결하면 데이터로부터 노이즈가 완화된 가중치가 학습되며, 이 가중치를 통해 노이즈가 완화된 투영맵을 테스 트 단계에서 쉽게 얻을 수 있다. 마지막 문제는 네트워크 과정 을 기존 거품 생성 알고리즘에 통합하여 거품 생성을 효과적 으로 표현한다.

2. 관련 연구

이번 장에서는 본 논문과 밀접하기 관련있는 물리 기반 시뮬레 이션 기반 거품 생성 기법, 스크린 공간을이용한 거품표현 기 법, 인공지능을 활용한 시뮬레이션 기법, 마지막으로 노이즈 제거를 위한 인공신경망 기법들에 대해 간략하게 살펴본다.

2.1 물리 기반 시뮬레이션을이용한 거품 모델링

물리 기반 시뮬레이션 분야에서 거품 생성과 움직임에 관한 연구들이 꾸준히 발표되고 있다. Takahashi 등은 기반 유체의 움직임을 곡률 기반으로 분석하여, 움직임이 큰 영역에 상태 변화 규칙을 적용함으로써 거품 효과를 표현혔다 [24]. 하지 만, 거품보다는 모래 알갱이와 유사한 입자 모션을 갖기 때 문에 다양한 거품 효과를 표현하기는 한계가 있다. Geiger 등 은 거품 생성과정을 효과적으로 처리하기 위해 다중레이어링 (Multilayering)방식을 제안했다 [25]. 거품, 스플래쉬, 물방울, 미스트(Mist) 등을 표현할 수 있는 레이어가 각각 계산되지만 거품이 뭉치는 문제가 발생한다. 또한, 거품 생성과 렌더링에 만 초점이 맞춰져 있어서 거품의 움직임을 사실적으로 표현하 기에는 충분하지 않기 때문에 다양한 장면에 활용하기 어려운 방식이다. 오일러리안(Eulerian) 모델을이용한 방식에서는 입 자-레벨셋(Particle level-set)이나 마커 입자(Maker-particle) 방 식을 활용하여 스플래쉬와 같은 2차 효과(Secondary effects)를 표현한다. Kim 등은 액체 표면으로부터 떨어진 마커 입자들 을 버리지 않고, 스플래쉬와 물방울로 표현할 수 있는 방법을 소개했다 [18]. 하지만, 대부분 탄도(Ballistic) 움직임을 갖기 때문에 디테일한 거품을 표현하기에는 한계가 있다. Losasso 등은 이 방법을 입자-레벨셋 기법으로 개선하여 스플래쉬를 표현하였으며, 탄도와 같은 움직임을 개선하기 위해 스플래쉬 입자들에 대해서 SPH(Smoothed particle hydrodynamics)기법을 적용하였다 [26]. 기존의 탄도 움직임에서는 표현하기 어려웠 던 현상인, 공기와 스플래쉬 입자 사이에 존재하는 확산 현상 (Diffuse phenomena)을 표현했다. 이 방법은 스플래쉬에만 초 점이 맞춰져 있으며, 거품은 텍스처를 활용하여 표현하였다.

Mihalef 등은 SPH기반으로 용존 가스(Dissolved gas) 문제를 풀었으며, 기존에 표현하기 어려웠던 탄산음료를 사실적으로 표현했다 [27]. Ihmsen 등은 SPH 프레임워크만을이용하여 스 플래쉬, 거품, 버블 등을 표현했다 [19]. 하지만, 결과의 품질이 입자 개수에 의존하기 때문에 고품질 결과를 제작하기 위해서 는 많은 개수의 SPH 입자를 요구하며, 그에 따라 계산시간이 증가한다. 또한, SPH 커널로 인해 거품 입자들이 뭉치는 문제 가 발생한다. Wang 등은 SPH와 Lattice Boltzmann 기법을 혼합 한 하이브리드 기법을 제안하여, Ihmsen 등의 방법을 효율적 으로 개선하였다 [28]. 하지만, 대부분 스플래쉬만 표현되며, 다른 효과는(거품, 버블 등) 거의 알아볼 수 없을 정도로 표현 이 제한적이다.

2.2 스크린 공간을 활용한 거품 모델링

스크린 공간을이용한 거품표현 방식은 게임이나 가상현실과 같은 실시간 애플리케이션에서 적극적으로 활용되고 있는 접 근법이다. Van der Laan 등은 격자 기반 접근법에서 나타나는 테셀레이션(Tessellation) 문제를 피하기 위해 스크린 공간에서 입자를 렌더링하는 새로운 프레임워크를 제안했다 [20]. 2D 스크린 공간에 투영할 때 나타나는 노이즈는 곡률 흐름 필터 (Curvature flow filtering) 기법을 통해 완화시켰다. 이 방법에서 거품 효과는 단순한 노이즈 텍스처를 이용하여 표현했으며, 사실적인 거품 효과를 기대하기는 어려운 방법이다. Bagar 등 은 서로 다른 형태의 유체를 별도의 레이어로 처리하여 좀 더 사실적이고 입체적인 거품 효과를만들어냈다 [21]. 이외에 스 크린 렌더링 기법은 다양한 방법으로 변형되었지만 [29, 30, 31], 2D 공간만을 활용하기 때문에 거품의 움직임까지 표현하 기에는 충분하지 않다.

이러한 문제를 해결하기 위해 Kim 등은 2D-3D인 두 가지 공간을 모두 활용하여 거품의 효율성과 품질을 개선했다 [22, 23]. 2D 공간을 이용하여 거품이 생성될 위치를 빠르게 찾고, 이 공간을 3D 공간으로 역변환(Inverse transformation)하여 거 품 입자를 이류시키는 방법이다.

2.3 인공신경망을이용한 시뮬레이션

최근에 인공신경망을이용하여 물리 기반 시뮬레이션을 하려 는 시도가 꾸준히 소개되고 있다. 특히 유체 시뮬레이션 분 야에서는 공통적으로 고해상도의 압력을 계산할 때 풀어야 하는 푸아송 방정식(Poisson equation)을 슈퍼 해상도(Super-resolution, SR)과정으로 대체함으로써 효율성을 극대화하려 고 노력했다 [32, 33, 34, 35]. 최근에는 딥러닝을 사용하여 고 해상도 시뮬레이션을 직접 처리하는 연구들도 제안되었다 : ConvNet 또는 GAN(Generative Adversarial Networks)을 사용 하여 시뮬레이션 디테일을 얻을 수 있는 접근법. Tompson 등 과 [36] Xiao 등 [37]은 Navier-Stokes 방정식을 효율적으로 풀기 위해 ConvNet 기반 접근법을 사용했다. 이 연구들에서는 시 뮬레이션 방정식을 직접 풀기보다는 이전에 획득한 저해상도 연기 시뮬레이션 결과를 사용하여 SR을 수행하였다.

ConvNet과 GAN은 SR관련 연구에 널리 사용되는 딥러닝 방 법이다. Dong 등은 단일 이미지 SR을 처리하기 위한 ConvNet 기반 해법을 제안했고 [38], Ledig 등과 [39] Chu 등 [40]은 이 미지 SR을위한 GAN 기반 방법을 제안했다. Chu와 Thüerey는 고해상도 연기 시뮬레이션을 합성하기 위해 ConvNet모델을 사용했고 [34], Werhah 등은 2D와 3D 연기 시뮬레이션을 SR하 기 위해 GAN을 활용했다. Bai 등은 딥러닝 기반의 동적 특징 (Dynamic features)을 활용하여 고해상도 연기의 디테일을 생 성할 수 있는 SR을 제안했다 [41]. 이런 다양한 접근법들이 존 재하지만 딥러닝을 스플래쉬나 거품에 적용한 사례는 없었다. 본 논문에서는 스크린 기반으로 거품을 생성할 수 있는 기존 프레임워크에서 고질적으로 나타나는 문제인, 노이즈한 투영 맵을 인공신경망을 통해 완화시킬 수 있는 방법을 제안한다. 결과적으로 우리의 방법은 거품의 디테일 손실 없이 고해상 도 거품 효과를 깔끔하게 표현할 수 있다.

2.4 노이즈 제거를 위한 인공신경망

이번 장에서는 본 논문과 밀접하게 관련있는 인공신경망 기 반 디노이징 기법에 대해 살펴본다. 이미지 데이터를 미리 설 정하는 접근법 대신 딥러닝 방법은 이미지 쌍의 대규모 셋을 이용하여 노이즈가 포함된 이미지에서 노이즈를 제거할 수있는 방식을 심층 신경망을 통해 직접적으로 학습한다. Jain 와 Seung은 5계층의 ConvNet을 이용한 노이즈 제거 방식을 제안했고 [42], 몇몇 연구들에서는 이 방식을 오토인코더(Autoencoder) 기반 방법으로 확장하였다 [43, 44]. 한편, Burger 등 은 [45] 다층 퍼셉트론을 사용하여 BM3D(Block-matching and 3D filtering) [46]와 유사한 성능을 보일 수 있는 방법을 제시했 다. Zhang 등은 DnCNN(Denoising ConvNet)을 제안하여 가우 시안 디노이징 문제를 해결할 수 있는 방법을 소개했다 [47]. Mao 등은 Symmetric skip connection을 사용하는 심층 완전 컨 볼루션 인코딩-디코딩 네트워크 기법을 제안했다 [48]. Tai 등 은 이미지 복원에 활용가능한 적응적 학습(Adaptive learning) 과정을 통해 메모리를 지속적으로 학습시킬 수 있는 메모리 네트워크(MemNet, Very deep persistent memory networks)를 제 안했다 [49]. 최근에는 NLRN [50], N3Net [51], UDNet [52] 모 두 노이즈 제거 작업을 용이하게 하기 위해 이미지의 지역 외 (Non-local) 속성을 DNN에 포함시켜서 사용하였다. 이외에 공 간적 변경 노이즈에 대한 유연성을 높이기 위해 노이즈 레벨 을 미리 평가하여 노이즈가 포함된 이미지와 함께 네트워크에 입력에 사용하는 FFDNet이라는 기법도 소개되었다 [53]. Guo 등 [54]과 Brooks 등은 [55] 둘다 카메라에서 이미지의 노이즈 제거과정을 시뮬레이션하려고 시도하였다. 하지만, 대부분의 디노이징 방법은 영상 데이터를 기반으로 이루어지며, 이러한 기법을 3차원 시뮬레이션 적용했을 경우 디테일까지 소실되 는 문제가 발생한다. 본 논문에서는 영상 데이터를 입력으로 사용하는 디노이징 네트워크를 사용했을 때 소실되는 거품 결과를 보여주고, 본 논문에서 제안하는 기법이 얼마나 정확 하게거품 입자를 표현하는지 실험을 통해 보여준다.

3. 제안하는 프레임워크

본 논문에서는 격자-입자 방식을 이용한 하이브리드 기법 중 하나인 FLIP(Fluid-implicit particle)기법을이용하여 기반 유체 시뮬레이션을 계산했으며, 이 방법을 통해 유체 입자를 이류 시킨다. 거품 생성은 이전에 제안된 스크린 공간 투영 기법을 사용했다 [22, 23]. 기본적인 거품 생성 방식에 대해서는 3.1장 에서 간단히 리뷰한 뒤, 본 논문에서 제안하는 방식에 대해서 자세하게 설명한다. 본 논문에서 제안하는 알고리즘은 아래와 같은 순서로 실행된다:

• 전처리과정

3D 유체 입자를 스크린 공간에 투영하고 이항 필터를 활용하여 네트워크의입력 데이터로 사 용될 데이터를 구축한다.
ConvNet기반의 디노이징 네트워크를 통해 투 영맵 데이터들을 학습한다. 향후, 이 과정은 투 영맵을 정제할 때 사용된다 (2번 과정에서 테스 트로 활용).

FLIP으로 이류된 유체 입자를 투영행렬을 통해 스크린 공 간에 투영한다. 유체 입자를 스크린 공간에 투영하는 과 정에서 입자의 물리량인 가속도와 깊이값을 투영한다.
디노이징 네트워크를 통해 두 가지 투영맵인, 가속도맵과 깊이맵을 정제한다.
정제된 가속도맵을이용하여 거품이 생성될만한 곳을입 자가 투영된 스크린 공간에서 빠르게 찾는다.
스크린 공간에서의 역변환을 통해 3D 공간에서 거품 입 자를 생성하고 이류시킨다.

3.1 스크린 공간 기반 거품표현 방식

3.1.1 유체 입자로부터 투영맵 생성

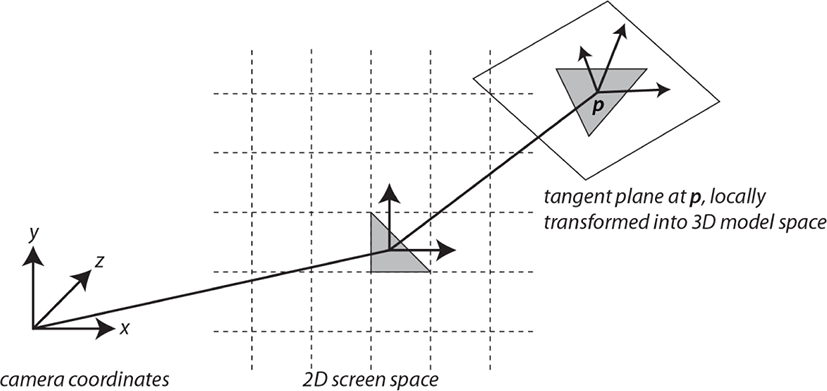
이번 장에서는 본 논문에서 활용하고 있는 스크린 공간 기반 거품 방식에 대해서 간단하게 설명한다 [22, 23]. 우선 3D 공간 에 존재하는 유체 입자들의 가속도와 깊이맵을 스크린 투영을 통해 계산한다. W 와 H는 각각 스크린 공간의 가로, 세로 픽셀 해상도를 나타낸다. N_x × N_y는 투영 간격인 h에 의해 나눠진 정규격자의 해상도이고, r은유체 입자의 반지름이다. 여기서 r은 투영시 부드러운 투영맵을 얻기위해 사용되는 범위이며, 사용자가 조절 가능한 값이다. 유체 입자의 깊이값인 z_ij와 가 속도인 d_ij는 투영 좌표로 변환되며 각각의 맵은 다음과 같이 구성된다 : 깊이맵 Z ∈ ℝ^N_x×N_y, 가속도맵 D ∈ ℝ^N_x×N_y. 입자 의 가속도 d_ij는 프레임 사이의 속도차이를 통해 간단히 계산 한다 : |v_t+Δt − v_t|.

3D 공간인 [x, y, z, 1]^T 에 존재하는 입자 x는 투영행렬 P를 이용하여 2D 투영 공간으로 변환된다 (Equation 1 참조).

[x ′ y ′ z ′ w] = P [x y z 1]

(1)

투영하는 과정에서 z값의 왜곡을 피하기 위해, z값을 제외 한 x, y에 대해서 원근 분할을 적용한다. 이 방식을 이용하여 3D 유체 입자의 투영 좌표인 (x_p, y_p), z_p와 투영된 가속도 d_p를 계산한다 (Equation 2 참조).

[x p y p z p] = [W ⋅ (12 + 12 x ′ / w) H ⋅ (12 + 12 y ′ / w) z ′] ︸ p r o j e c t e d c o o r d i n a t e s a n d d e p t h, [x d y d d p] = [x p y p d] ︸ a c c e l e r a t i o n,

(2)

여기서 (x_d, y_d)는 스크린 공간에서 가속도인 d_p가 저장된 배 열의인덱스이다.

3D 공간에서의 입자 반지름 r은 다음과같은 방법을이용하 여 투영한다 (Equation 3 참조):

[r x r y r z] = [r W p 1, 1 2 + p 1, 2 2 + p 1, 3 2 / w r H p 2, 1 2 + p 2, 2 2 + p 2, 3 2 / w r p 3, 1 2 + p 3, 2 2 + p 3, 3 2],

(3)

여기서 p_i,j는 투영행렬 P의 요소이다. 등방성하게 투영된 반 지름값을 얻기 위해서 r_x와 r_y를 r_p로 설정하였다.

많은 개수의유체 입자들이 스크린 공간의 한 노드에 투영될 수 있기 때문에 깊이와 가속도값을 다음과같이 업데이트한다 (Equation 4 참조):

z i j ← min (z i j, z p − r z h i j), d i j ← arg min (z i j)

(4)

여기서

h i j = 1 − (i h − x p) 2 + (j h + y p) 2 r p 2

(5)

위 수식에서 $(i h − x p) 2 + (j h − y p) 2 ≤ r p 2$ 는 투영된 좌표가 투영 공간의 각 노드에 영향을 받는지 여부를 확인하기 위한 조건이다. 투영된 좌표의 깊이값인 z_p − r_zh_ij가 z_ij보다 작다 면, Equation 4를 이용하여 z_ij와 d_ij를 업데이트한다. 3D 입자가 스크린 공간에 투영된 가속도맵은 Figure 2에서도 볼 수 있 다. 하지만 앞에서 언급했듯이 에일리어싱 문제가 발생하며 3.2~3.3장에서는 이 문제를 효율적으로 처리할 수 있는 방법 에 대해 설명하고, 제안하는 기법을 이전 기법과 통합한 거품 입자의 생성과 이류에 대해서는 3.4장에서설명한다.

3.2 전처리 과정: 투영맵 데이터 수집

본 논문에서는 네트워크 학습을 위해 필요한 데이터는 물리 기반 시뮬레이션을 통해 획득하였다. 거품 효과를 표현할 수 있는 접근법은 다양하지만 인공신경망을 통해학습을 하기 위 해서는 Kim 등이 제안한 방법이 2D 공간을 같이 활용하기 때 문에 우리는 이 방법을 기반으로 데이터를 수집한다 [22, 23]. 에일리어싱을 완화하기 위해 본 논문에서는 분리 가능한 이항 필터(Separable binomial filter)를 이용하여 데이터를 정제한다 (Figure 4 참조).

Figure 4: Separable binomial filter with size n_filter=3. Acceleration value (i, j) shown in the center is the weighted sum of neighboring values.

Download Original Figure

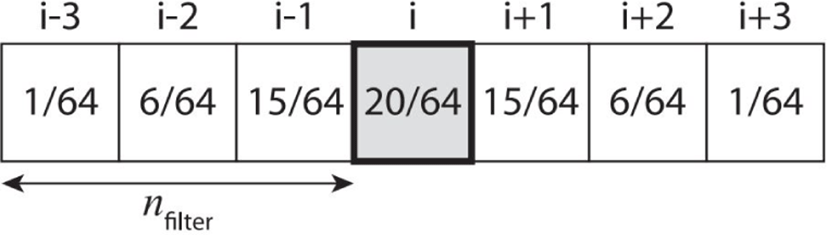
이 필터는 에일리어싱 문제가 포함된 투영맵을 스무딩 과정 으로 완화시키는 역할을 한다. 스무딩 매개 변수 n_filter는 사용 자가 설정 가능하며 d_ij ≠ ∞인 곳에 모두 적용된다. 본 논문에 서는 오버 스무딩으로 인한 거품 손실을 최소화하기 위해 d_ij 의 크기에 따라 필터의 크기가 제어되도록 하였다 (Equation 6 참조).

n filter ∗ = {| d i j | α, if | d i j | > η 3, else

(6)

여기서 α는 사용자가 제어 가능한 변수로, 본 논문에서는 12 로 설정하였다.

Figure 5는 가속도맵에 이항 필터를 사용하기 전과 후의 결 과이다. 거친형태가 보이는 가속도맵이 (Figure 5a 참조), 필터 를 적용한 후에는 특징적인 형상은 유지한 채 스무딩된 결과를 보여준다 (Figure 5b 참조). 본 논문에서는다음과같은 방식 으로 다양한 거품 장면에 대해서 투영맵에 대한 쌍을 구축하 였다.

Figure 5: Comparison of aliasing artifacts. The pixels are colored according to the magnitude of d_ij from red(high) to the blue(low).

Download Original Figure

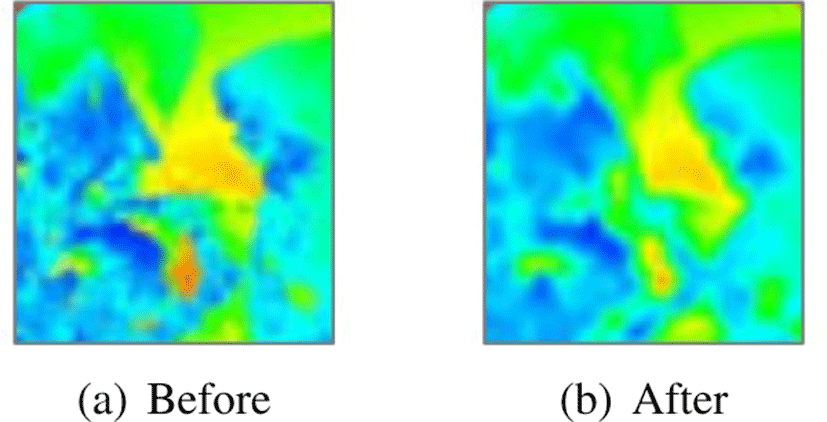
Figure 6은 데이터를 구축하기 위해 사용한 장면들이다. 유 체에 의한 거품 시뮬레이션 뿐만 아니라, 고체와의 충돌에 의 해 생성되는다양한 장면들에서 계산한 투영맵(가속도, 깊이) 을 이용하여 데이터를 구축한다. 데이터 개수는 가속도와 깊 이맵 각각 5,000개의 투영맵을 사용했으며, 필터링된 개수까 지 포함하면 20,000개의 데이터를 학습데이터로 사용하였다.

Figure 6: Examples by simulation.

Download Original Figure

3.3 디노이징 네트워크를 이용한 투영맵 정제

물리 기반 시뮬레이션을이용하여 거품 데이터인 {F⁰, F¹, ...} 를 얻은 뒤, 이전 장에서 설명한 방법을 이용하여 이항 필터 를 적용하지 않은 투영맵인 ${δ f w o 0, δ f w o 1, …}$ 와 필터를 적용한 투영맵인 ${δ f w 0, δ f w 1, …}$ 를 각각 생성한다. 여기서 δ는 앞에서 설명한 D와 Z를 나타낸다. 투영맵들을 학습 네트워크에 넣기 전에 패치 단위로 분할한다. 학습 데이터가 주어지면, 우리의 목표는 예측값 ν_s와 GT(Ground truth) δ_fw 사이의 손실을 최소 화하는 매핑함수 f(x)를 찾는 것이다. 이 과정을 수행하기 위 한 손실함수는 예측된 투영맵과 GT 투영맵 사이의 MSE(Mean squared error)이다. 우리의 목표는 ν_s = f(x)를 최소화하는 것이다.

SRCNN(Super-resolution CNN)기법에서는 많은 가중치 레이 어들을 사용하면 큰 메모리를 요구하기 때문에 깊은 네트워 크를 구성하는데 한계가 있다 [38]. 이 같은 문제를 피하기 위 해 본 논문에서는 잔차 학습(Residual learning)을 통해 거품 데 이터를 학습/테스트한다. 입출력 투영맵의 잔차맵은 다음과 같이 계산한다 : r = δ_fw − δ_fwo. SRCNN 기법에서의 손실함 수는 $12 ‖ δ f w − f (x) ‖ 2$ 이지만, 본 논문에서는 잔차맵을 예측하 고 싶기 때문에 최종적인 손실함수 L을 다음과같이 계산한다 (Equation 7 참조).

L (r, x) = 12 ‖ r − x ‖ 2

(7)

여기서 r은 잔차이고, x는 f(x)의 값이다. 네트워크과정에서 손실 레이어는 잔차 추정, δ_fwo, δ_fw 인 3가지 요소를 이용하여 계산된다. 손실은 네트워크를 통해 복원된 맵과 δ_fw 사이의 유클리디안 거리(Euclidean distance)로 계산되며, 여기서 복원된 맵은 네트워크의입력과 출력맵의 합이다.

이 네트워크는 ConvNet기반으로 모델링되었으며 다음과같 은 구성으로 되어있다 (Figure 7 참조): 첫번째 컨볼루션(Convolution) 연산이 끝난 특징맵을 이후 2번의 컨볼루션을 거쳐 나온 결과값에 다시 더해주는 잔차 보완 방법으로 디자인하였다. 이 과정에서는 컨볼루션 연산을 통해 손실된 오차를 잔차 보완을 통해 완화한다. 본 논문에서는 이 과정을 10번 반복했 으며, 한 번의 주기당 2개의 컨볼루션을 거치므로 총 20번의 컨볼루션 연산이 진행된다. 처음에는 첫 컨볼루션이 끝난 값 이 더해지지만, 이후에는 반복적으로 이전 결과값이 더해진 다. 그 다음 업스케링을 통해 크기를 2배로 키우고, 이후 4번의 컨볼루션 연산을 끝으로 종료된다. 이렇게 얻어진 투영맵인 D*와 Z*는 거품 입자의 생성을 결정하는데 활용되며, 다음장 에서 자세히 설명한다.

Figure 7: VGG19 neural network structure (red arrow : residual process).

Download Original Figure

3.4 기존접근법과의 통합

3.4.1 거품 입자의 생성과 이류

정제된 투영맵을 활용하여 거품이 생성될 만한 2D 후보 영역 을 추출한다 (Equation 8 참조).

C = {(i, j, k) | d > γ, z ∈ Z ∗, d ∈ D ∗, (i, j) ∈ ℝ N x × N y},

(8)

여기서 γ는 빠른 유동 영역을 찾는데 사용되는 임계값이며, 본 논문에서는 0.0001로 설정하였다. Z*와 D*는 네트워크를 통해 정제된 깊이와 가속도맵이다. γ값을 줄이면 유동이 느 린 영역에서도 거품을 생성할 수 있으며, 사용자가 거품 양을 쉽게 제어할 수 있다. 추출된 2D 거품 영역을 삼각형으로 구성 하기 위해 마칭 스퀘어(Marching squares) 알고리즘을 사용하 였으며 [31], 결과적으로 거품 입자의 후보군은 2D 삼각형으 로 구성된다. 이러한 삼각형들은 Equations 1과 2의 역변환을 통해 3D 모델공간으로 변환된다. 변환된 삼각형의 좌표는 다 음과같이 계산한다 (Equation 9 참조).

[x y z 1] = Q [(− 1 + 2 x p / W) w (− 1 + 2 y p / H) w z p w],

(9)

여기서

w = 1 − q 4, 3 z p q 4, 1 (− 1 + 2 x p / W) + q 4, 2 (− 1 + 2 y p / H) + q 4, 4,

(10)

여기서 q_i,j는 역투영행렬(Inverse projection matrix) Q의 요소 이며, 앞에서 언급했듯이 원근 분할은 z_p에 적용되지 않는다. 거품입자의 개수는 Weber number를 통해 결정되며 좀 더 자세 한 방식은 Kim 등의 논문을읽어보길 권장한다 [22, 23].

그 다음 과정으로 정제된 투영맵을 이용하여 거품의 웨이 브 패턴을 계산한다. 먼저 Van der Lann 등이 제안한 방법을 활용하여 투영된 공간의 모든 값에서 유동 기반 곡률을 계산 한다 [20] (Equation 11).

∂ z ∂ t = H,

(11)

여기서 t는 타임 스텝이며, H는 2D 투영공간에서 계산한 깊 이맵의 평균 곡률이다. 이 과정에서 사용한 깊이맵은 Z*이다. Van der Lann 등의 방법은 노이즈 패턴을 내포하고 있고 [20], 이를 완화하기 위해서는 반복적으로 곡률을 계산해야한다. 이 러한 접근은 원본 곡률의 변화 패턴을 지워버리기 때문에 본 논문에서는 Equation 8을 다음과같이 수정하여 거품의 웨이브 패턴을 계산한다 (Equation 12 참조).

C ∗ = {(i, j, k) | d > γ ∩ ​ f > β, f ∈ F ∗, (i, j) ∈ ℝ N x × N y},

(12)

여기서 F*는 깊이맵의 곡률이며, 여기서 사용한 깊이맵은 네 트워크를 통해 정제된 Z*를 이용하였다. 또한, β는 높은 곡률 영역을 찾기 위한 임계값으로, 본 논문에서는 0.1로 설정하였 다. 거품입자에 대한 이류는 FLIP 해법을 통해 계산된 격자의 속도장과 유체 입자들을 활용하였다. 이 방식은 이전 접근법 을 그대로 이용하였으며 좀 더 자세한 설명은 이전 논문을 읽 기를 권장한다 [22, 23].

4. 구현

시뮬레이션과 렌더링에 대한 상세내역. 본 논문은 다음과 같 은 환경에서 구현되었다 : 인텔 i7-7700k 4.20GHz. CPU 32GB RAM, NVIDIA GeForce GTX 1080 Ti 그래픽카드. FLIP기반 유 체 해법을 기반 유체 시뮬레이션으로 사용했으며 [56], 유체 의 압력을 계산하는 수치적 행렬해법은 GPU기반 선조건 적 용 컬레 기울기법(Preconditioned conjugate gradient)을 이용하 였다 [57]. FLIP 격자의 경우 모든 운동량은 Staggered Marker-and-Cell 방법을 사용하여 저장했으며 [58], 유체와 고체의 충 돌처리를 위해 Akinci 등이 제안한 경계입자(Boundary particle) 기법을 사용하였다 [59].

결과를 제작하기 위해 본 논문에서는 유체의 표면 재복원은 하지 않고 입자를 레이트레이싱하여 렌더링하였다. 유체 입자 의 색은 (0.8, 0.5, 0.3), 거품 입자의 색은 (1.0, 1.0, 1.0)로 각각 설정하였으며, 알파값은 0.07로 사용하였다. 각 입자를 렌더링 될 이미지 공간에 투영하고, 투영된 위치로부터 3×3 픽셀들을 다음과같이 업데이트한다 (Equation 13 참조).

p i, j = {p i, j r ← c a c r + (1 − c a) p i, j r p i, j g ← c a c g + (1 − c a) p i, j g p i, j b ← c a c b + (1 − c a) p i, j b,

(13)

여기서 $(p i, j r, p i, j g, p i, j b)$ 는 픽셀의 색상이며,(c_r, c_g, c_b)는 이미지 공간에 투영된 입자의 색상이고, c_a는 알파값이다. 거품 시뮬 레이션 알고리즘의 의사코드는 다음과 같다 (Algorithm 1 참 조).

Algorithm 1 : Pseudo-code of our algorithm

for each frame do

// Base water solver

Advect 3D water partices using FLIP

Compute the interaction of water & solids

// Our foam simulation

Project 3D water particles on screen space

Denoising of projection maps with neural network

Extract wave patterns by curvature

Find 2D foam-sourcing areas

Find 3D foam-sourcing triangles

Emit foam particles

Advect foam particles

Compute the interaction of foam & solids

Eliminate expired foam particles

end for

VGG19 인공신경망에 대한 상세내역. 본 논문에서는 VGG19 인공신경망을 사용하여 디노이징 네트워크를 디자인 하였고, 이번 장에서는 VGG19 네트워크를 개발할 때의 상세 내역에 대해서 설명한다. VGGNet 모델은 크게 2가지 단계로 구성되어있다 : VGG network와 Reconstruction. 예를 들어, 입 력 이미지로 128×128 해상도를 갖는 3채널 이미지라고 했을 때, 입력 x는다음과같다 : x(128, 128, 3).

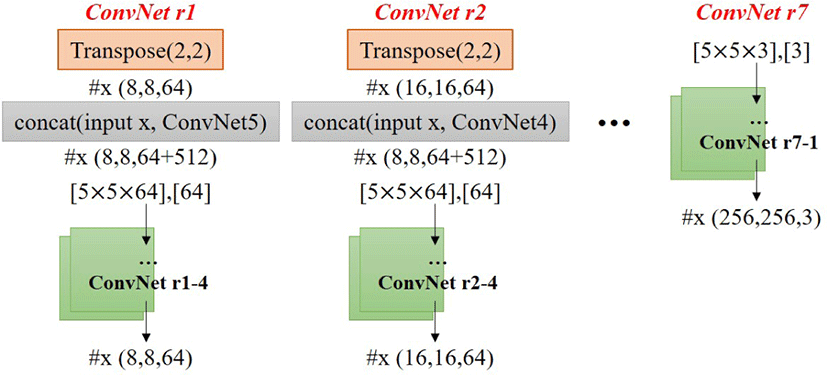
첫번째 ConvNet1은 앞에서설명했듯이 2개의 ConvNet 레이 어로 구성되어있으며, 이때 사용한 Weight와 Bias 크기는다음 과 같고 (5×5×64, 64), ConvNet1의 출력값인, 너비(Width), 높 이(Height), 깊이(Depth)는 각각 (64, 64, 64)이다. 여기서 사용 한 활성화 함수는 ReLU이다. ConvNet1의 출력값은 ConvNet2 의입력으로 사용되며, 전체적인 VGGNet 모델은 다음과같다 (see Figure 8). 이 그림에서 ConvNet 1-2라는 것은 ConvNet 1 과정에서 ConvNet 레이어를 2개 사용한다는 의미이고, 마찬 가지로 ConvNet 5-4는 ConvNet 5과정에서 ConvNet 레이어를 4개 사용한다는 의미이다.

Figure 8: VGG network (input : x(128, 128, 3), output : x(4, 4, 512), [weight],[bias], #x(width, height, depth)).

Download Original Figure

Reconstruction 단계에서는 VGG network의 출력값에 대한 전치 컨볼루션(Transposed convolution)을 통해 결과를 복원하 는 과정이다 (Figure 9 참조). ConvNet r1에서 ConvNet r7까지의 세부 내역은 Table 1과 같이 설정하였다. 인공신경망의 입력 이 원본 맵의 $12$ 크기이며, 향후 잔차맵과 더해질 때 Reconstruction의 출력과 동일한 크기에서 더해진다. 이 네트워크는 텐서 플로우에서 구현하였으며 [60], 여기서 사용한 옵티마이저는 Adam(Adaptive moment estimation)이고, 학습과정에서는 옵티 마이저는 총 5,000번 반복하였으며, 최종학습에서의 손실값은 9.81이다.

Figure 9: Reconstruction (input : x(4, 4, 512), output : x(256, 256, 3)).

Download Original Figure

Table 1: Configuration of reconstruction model in VGG 19.

	ConvNet r1	ConvNet r2	ConvNet r3	ConvNet r4	ConvNet r5	ConvNet r6	ConvNet r7
Transpose(...)	(2,2)	(2,2)	(2,2)	(2,2)	(2,2)	(2,2)	–
#x(w,h,d)	(8,8,64)	(16,16,64)	(32,32,64)	(64,64,64)	(128,128,64)	(256,256,64)	–
concat(...)	(input x, ConvNet5)	(input x, ConvNet4)	(input x, ConvNet3)	(input x, ConvNet2)	(input x, ConvNet1)	–	–
#x(w,h,d)	(8,8,64+512)	–	–	–	–	–	–
[weight],[bias]	5×5×64,64	5×5×64,64	5×5×64,64	5×5×64,64	5×5×64,64	5×5×64,64	5×5×3,3
Num. ConvNet	ConvNet r1-4	ConvNet r2-4	ConvNet r3-4	ConvNet r4-2	ConvNet r5-2	ConvNet r6-2	ConvNet r7-1
#x(w,h,d)	(8,8,64)	(16,16,64)	(32,32,64)	(64,64,64)	(128,128,64)	(256,256,64)	(256,256,3)

Download Excel Table

5. 결과 및 토론

본 논문에서 제안하는 기법을 다양한 방면으로 분석하기 위해 이미지 기반 디노이징 기법과의 결과 품질과 연속성 측면에서 의 오차를 비교하였다.

먼저제안하는 기법의 우수성을입증하기 위해 간단한 테스 트 시나리오로,2개의 박스가 액체를 휘젓는 장면을 제작했다. 이 장면에서 유체를 표현하기 위해 타임 스텝은 0.006으로 설 정하고, 약 80만개의 유체 입자들을 사용하였다. Figure 10은 가속도맵을 정제한 결과이다. 입력으로 사용된 투영맵은 거 친 노이즈뿐만 아니라, 스크린에 투영된 결과가 에일리어싱 형태로 표현된 것을 볼 수 있다. 제안한 네트워크를 통해 정제 된 투영맵은 에일리어싱 문제를 완화시켰을 뿐만 아니라 원본 가속도맵의 형태를 잘유지했다.

Figure 10: Refinement of acceleration map with our method (white : fast flow zone).

Download Original Figure

Figure 11: Acceleration map improvement using VDNet [] and foam effects using it.

Download Original Figure

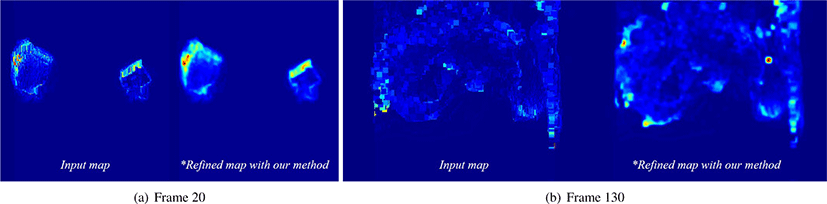
Figure 12은 정제된 투영맵을 이용하여 생성한 거품 효과이 다. 정제 과정으로 인한 추가적인 노이즈나 거품 손실 없이 안 정적으로 거품 결과를 만들어냈다. 특히, Figure 12b에서는 뿌 옇게 퍼지는 표면 거품(Surface foam) 효과가 명확하게 잘 표현 되었다. 이장면을 만들 때, Kim 등이 제안한 거품 이류 기법을 사용했으며 [22], 제안한 투영맵 정제기법은 얇고 뿌옇게 퍼지 는 표면 거품도 소실없이잘 표현했다.

Figure 12: Rotating two boxes in water with our method (inset image : simulation view).

Download Original Figure

본 논문에서는 가우시안 노이즈 모델에서 동작하는 유명한 방법인 DnCNN(Denoising CNN) [47]와 VDNet(Variational Denoising Networks) [61]을 우리의 방법과 비교하였다. 각 방법에 시 제시한 데이터와 알고리즘을이용하여 학습시켰으며, 테스 트 과정에서 유체 입자을 이용하여 계산한 투영맵을입력으로 사용하여 디노이징 결과를 얻어냈다. 출력 결과인 디노이징 맵은 앞에서설명한 것과 같이 역변환을 통해 3차원 공간에서 거품 입자를 생성하는데 활용되며, 이 과정에서 최종적으로 표현된 거품 결과를 비교하였다.

Figure 13는 Deep CNN 기반으로 이미지 디노이징을 수행하 는 네트워크인 DnCNN [47]을 활용하여 거품 시뮬레이션에 적용한 결과이다. 입력 가속도맵에 비해 노이즈가 완화된 결과 를 만들어냈지만, 작은 움직임을 갖는 거품들을 대부분 소실 시키기 때문에 거품의 디테일이 떨어진다. 또 다른 이미지 디 노이징 기법 중 하나인 VDNet [61]을 거품 시뮬레이션 적용하 여 우리의 방법과 비교하였다 (Figure 11 참조). 앞에서의 결과 와 마찬가지로 거품이 소실되는 문제가 발생하였다. Figure 15 는 앞에서의 결과를 프레임별로 비교한 결과이다. 우리의 디 노이징 네트워크는 작은 스케일 거품임에도 디테일 요소를 놓 치지 않고 전체적으로 잘 표현했다.

Figure 13: Acceleration map improvement using DnCNN [] and foam effects using it.

Download Original Figure

5.1 디노이징에 따른 연속성 비교

결과에서 보여주듯이 우리의 방법은 거품 소실을 최소화하여 디테일을 향상시켰다. 하지만 시계열 데이터와 같은 애니메이 션 데이터이기 때문에 소실 뿐만 아니라 깜박이는 문제가 발 생한다. 이번 장에서는 우리의 방법, DnCNN [47], VDNet [61] 접근법에서 깜빡이는 문제가 각각 얼마나 발생하는지 비교한다. 프레임간의 깜빡이는 정도를 계산하기 위해 우리는 간단 하게 다음과같이 에러를 측정하였다 : $‖ f t − f t + Δ t ‖ Δ t$ .

Figure 14은 프레임간의 연속성을 비교한 결과이다. 그림에 서 보듯이 우리의 방법이 노이즈가 완화된 결과를 가장 잘 보 여주었다. 반면에 이전 기법들은 프레임간의 노이즈가 심하게 나타나는 것을 볼 수 있다. 이 결과는 현재 프레임에 해당하는 에일리어싱을 보여주는게 아닌, 시간 변화에 따른 노이즈를 보여주는 결과이다. 우리의 방법은 투영맵에 생성되는 에일 리어싱 뿐만 아니라, 프레임간의 노이즈도 완화시킨 것을 잘 보여준다.

Figure 14: Continuity test at 164 frame. The pixel was colored from red (high) to blue (low) depending on the magnitude of difference between frames.

Download Original Figure

5.2 스크린 투영 방식과의 통합과 확장성

본 논문에서는 다양한 거품 생성 알고리즘 중에 스크린 공간 방식을 채용했으며, 그 이유와 확장 가능성에 대해 설명한다. 대부분의 거품 입자 생성 방식은 기반 유체의 움직임을 분석 하기 위해 모든 격자 또는 입자의 운동량에 접근해야 한다. 이 과정은 오일러리안(Eulerian)과 라그랑지안(Lagrangian) 접 근법에서도 모두 필요한 과정이다. 특히 물 속에 존재하는 버 블과 달리 거품은 유체 표면에 생성되는 특징이 있기 때문에 우리는 스크린에 유동을 투영하여 거품을 생성하는 기법을 활 용하였다 [22, 23]. 이 방식은 2D 투영맵의 품질과 해상도에 따 라 거품품질이 결정되기 때문에 본 논문에서 제안하는 방법과 잘 맞는다. 본 논문에서는 거품 생성을 목표로 결과 비교를 했 지만, 스크린 스페이스 렌더링 기법을 주로 사용하는 게임과 같은 실시간 애플리케이션에 활용이 가능하다 [30, 20, 62, 63].

6. 결론

본 논문에서는 물 시뮬레이션에서 표현되는 거품 생성을 효율 적으로 표현할 수 있는 스크린 투영 방식과 디노이징 네트워 크 아키텍처를 제안했다. 투영맵을 정제하기 위해 전처리 과 정에서 데이터를 수집하고, 잔차기반의 네트워크를 이용하여 노이즈를 완화시킬 수 있는 방법을 소개했다. 이 네트워크를 통해 거품생성에 영향을 주는 Z*, D*, F*를 새롭게 계산하였 다. 다양한 장면에서 실험했을 때, 이항 필터만을 사용한 결 과보다 본 논문에서 제안하는 네트워크 기법이 노이즈 제거 면에서 개선된 결과를 보여주었다 (Figure 3 참조). 이 같은 이 유로는 1) 적응적으로 필터의 크기를 조절하는 n_filter의 활용과, 2) 비선형 활성화 함수 기반의 네트워크 학습 과정을 통해 이 항 필터만 사용했을 때보다 나은 결과를 보여주었다. 이미지 디노이징에 활용하는 기존 기법들에서는 작은 크기의 거품들 이 온전히 표현되지 못하고 사라지는 반면, 제안하는 방법은 소실없이 작은 거품들까지 안정적으로 잘 표현했다. 향후로는 적응형 데이터 자료구조를 이용하여 유동 레벨에 따라 투영맵 을 정제시키는 방법으로 확장할 예정이다.

Figure 15: Comparison results of our method and previous approaches (left to right frame number : 20, 130, 180).

Download Original Figure

참고 문헌

[1].

N. Chentanez and M. Müller, “Real-time eulerian water simulation using a restricted tall cell grid,” in ACM Siggraph 2011 Papers, 2011, pp. 1–10.

[2].

C. Jiang, C. Schroeder, A. Selle, J. Teran, and A. Stomakhin, “The affine particle-in-cell method,” ACM Transactions on Graphics (TOG), vol. 34, no. 4, pp. 1–10, 2015.

[3].

M. Cha, J. Lee, B. Choi, H. Lee, and S. Han, “A data-driven visual simulation of fire phenomena,” in SIGGRAPH’09: Posters, 2009, pp. 1–1.

[4].

P. Beaudoin, S. Paquet, and P. Poulin, “Realistic and controllable fire simulation,” in Graphics Interface, vol. 2001, 2001, pp. 159–166.

[5].

D. Q. Nguyen, R. Fedkiw, and H. W. Jensen, “Physically based modeling and animation of fire,” in Proceedings of the 29th annual conference on Computer graphics and interactive techniques, 2002, pp. 721–728.

[6].

N. Rasmussen, D. Q. Nguyen, W. Geiger, and R. Fedkiw, “Smoke simulation for large scale phenomena,” in ACM SIGGRAPH 2003 Papers, 2003, pp. 703–707.

[7].

R. Setaluri, M. Aanjaneya, S. Bauer, and E. Sifakis, “Sp-grid: A sparse paged grid structure applied to adaptive smoke simulation,” ACM Transactions on Graphics (TOG), vol. 33, no. 6, pp. 1–12, 2014.

[8].

R. Fattal and D. Lischinski, “Target-driven smoke animation,” in ACM SIGGRAPH 2004 Papers, 2004, pp. 441–448.

[9].

T. Kim, E. Hong, J. Im, D. Yang, Y. Kim, and C.-H. Kim, “Visual simulation of fire-flakes synchronized with flame,” The Visual Computer, vol. 33, no. 6, pp. 1029–1038, 2017.

[10].

J.-H. Kim and J. Lee, “Fire sprite animation using fire-flake texture and artificial motion blur,” IEEE Access, vol. 7, pp. 110 002–110 011, 2019.

[11].

M. Choi, J. A. Wi, T. Kim, Y. Kim, and C.-H. Kim, “Learning representation of secondary effects for fire-flake animation,” IEEE Access, vol. 9, pp. 17 620–17 630, 2021.

[12].

B. Kim, Y. Liu, I. Llamas, X. Jiao, and J. Rossignac, “Simulation of bubbles in foam with the volume control method,” ACM Transactions on Graphics (TOG), vol. 26, no. 3, p. 98, 2007.

[13].

O. Busaryev, T. K. Dey, H. Wang, and Z. Ren, “Animating bubble interactions in a liquid foam,” ACM Transactions on Graphics (TOG), vol. 31, no. 4, pp. 1–8, 2012.

[14].

J.-M. Hong, H.-Y. Lee, J.-C. Yoon, and C.-H. Kim, “Bubbles alive,” ACM Transactions on Graphics (TOG), vol. 27, no. 3, pp. 1–4, 2008.

[15].

D. Kim, O.-y. Song, and H.-S. Ko, “A practical simulation of dispersed bubble flow,” in ACM SIGGRAPH 2010 papers, 2010, pp. 1–5.

[16].

F. Dagenais, J. Gagnon, and E. Paquette, “An efficient layered simulation workflow for snow imprints,” The visual computer, vol. 32, no. 6, pp. 881–890, 2016.

[17].

M. B. Nielsen and O. Østerby, “A two-continua approach to eulerian simulation of water spray,” ACM Transactions on Graphics (TOG), vol. 32, no. 4, pp. 1–10, 2013.

[18].

J. Kim, D. Cha, B. Chang, B. Koo, and I. Ihm, “Practical animation of turbulent splashing water,” in Symposium on Computer Animation, 2006, pp. 335–344.

[19].

M. Ihmsen, N. Akinci, G. Akinci, and M. Teschner, “Unified spray, foam and air bubbles for particle-based fluids,” The Visual Computer, vol. 28, no. 6, pp. 669–677, 2012.

[20].

W. J. van der Laan, S. Green, and M. Sainz, “Screen space fluid rendering with curvature flow,” in Proceedings of the 2009 symposium on Interactive 3D graphics and games, 2009, pp. 91–98.

[21].

F. Bagar, D. Scherzer, and M. Wimmer, “A layered particle-based fluid model for real-time rendering of water,” in Computer Graphics Forum, vol. 29, no. 4, 2010, pp. 1383–1389.

[22].

J.-H. Kim and J. Lee, “Synthesizing large-scale fluid simulations with surface and wave foams via sharp wave pattern and cloudy foam,” Computer Animation and Virtual Worlds, vol. 32, no. 2, p. e1984, 2021.

[23].

J.-H. Kim, J. Lee, S. Cha, and C.-H. Kim, “Efficient representation of detailed foam waves by incorporating projective space,” IEEE transactions on visualization and computer graphics, vol. 23, no. 9, pp. 2056–2068, 2016.

[24].

T. Takahashi, H. Fujii, A. Kunimatsu, K. Hiwada, T. Saito, K. Tanaka, and H. Ueki, “Realistic animation of fluid with splash and foam,” in Computer Graphics Forum, vol. 22, no. 3, 2003, pp. 391–400.

[25].

W. Geiger, M. Leo, N. Rasmussen, F. Losasso, and R. Fedkiw, “So real it’ll make you wet,” in ACM SIGGRAPH 2006 Sketches, 2006, p. 20.

[26].

F. Losasso, J. Talton, N. Kwatra, and R. Fedkiw, “Two-way coupled sph and particle level set fluid simulation,” IEEE Transactions on Visualization and Computer Graphics, vol. 14, no. 4, pp. 797–804, 2008.

[27].

V. Mihalef, D. Metaxas, and M. Sussman, “Simulation of two-phase flow with sub-scale droplet and bubble effects,” in Computer Graphics Forum, vol. 28, no. 2, 2009, pp. 229–238.

[28].

C.-b. Wang, Q. Zhang, F.-l. Kong, and H. Qin, “Hybrid particle–grid fluid animation with enhanced details,” The Visual Computer, vol. 29, no. 9, pp. 937–947, 2013.

[29].

N. Truong and C. Yuksel, “A narrow-range filter for screen-space fluid rendering,” Proceedings of the ACM on Computer Graphics and Interactive Techniques, vol. 1, no. 1, pp. 1–15, 2018.

[30].

N. Akinci, A. Dippel, G. Akinci, and M. Teschner, “Screen space foam rendering,” 2013.

[31].

M. Müller, S. Schirm, and S. Duthaler, “Screen space meshes,” in Proceedings of the 2007 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2007, pp. 9–15.

[32].

B. Kim, V. C. Azevedo, N. Thuerey, T. Kim, M. Gross, and B. Solenthaler, “Deep fluids: A generative network for parameterized fluid simulations,” in Computer Graphics Forum, vol. 38, no. 2, 2019, pp. 59–70.

[33].

Y. Xie, E. Franz, M. Chu, and N. Thuerey, “tempogan: A temporally coherent, volumetric gan for super-resolution fluid flow,” ACM Transactions on Graphics (TOG), vol. 37, no. 4, pp. 1–15, 2018.

[34].

M. Chu and N. Thuerey, “Data-driven synthesis of smoke flows with cnn-based feature descriptors,” ACM Transactions on Graphics (TOG), vol. 36, no. 4, pp. 1–14, 2017.

[35].

M. Werhahn, Y. Xie, M. Chu, and N. Thuerey, “A multi-pass gan for fluid flow super-resolution,” Proceedings of the ACM on Computer Graphics and Interactive Techniques, vol. 2, no. 2, pp. 1–21, 2019.

[36].

J. Tompson, K. Schlachter, P. Sprechmann, and K. Perlin, “Accelerating eulerian fluid simulation with convolutional networks,” in International Conference on Machine Learning, 2017, pp. 3424–3433.

[37].

X. Xiao, Y. Zhou, H. Wang, and X. Yang, “A novel cnn-based poisson solver for fluid simulation,” IEEE transactions on visualization and computer graphics, vol. 26, no. 3, pp. 1454–1465, 2018.

[38].

C. Dong, C. C. Loy, K. He, and X. Tang, “Image super-resolution using deep convolutional networks,” IEEE transactions on pattern analysis and machine intelligence, vol. 38, no. 2, pp. 295–307, 2015.

[39].

C. Ledig, L. Theis, F. Huszár, J. Caballero, A. Cunningham, A. Acosta, A. Aitken, A. Tejani, J. Totz, Z. Wang et al., “Photo-realistic single image super-resolution using a generative adversarial network,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4681–4690.

[40].

M. Chu, Y. Xie, L. Leal-Taixé, and N. Thuerey, “Temporally coherent gans for video super-resolution (tecogan),” arXiv preprint arXiv:1811.09393, vol. 1, no. 2, p. 3, 2018.

[41].

K. Bai, W. Li, M. Desbrun, and X. Liu, “Dynamic upsampling of smoke through dictionary-based learning,” arXiv preprint arXiv:1910.09166, 2019.

[42].

V. Jain and S. Seung, “Natural image denoising with convolutional networks,” Advances in neural information processing systems, vol. 21, 2008.

[43].

F. Agostinelli, M. R. Anderson, and H. Lee, “Adaptive multi-column deep neural networks with application to robust image denoising,” in Advances in neural information processing systems, 2013, pp. 1493–1501.

[44].

J. Xie, L. Xu, and E. Chen, “Image denoising and inpainting with deep neural networks,” in Advances in neural information processing systems, 2012, pp. 341–349.

[45].

H. C. Burger, C. J. Schuler, and S. Harmeling, “Image denoising: Can plain neural networks compete with bm3d?” in 2012 IEEE conference on computer vision and pattern recognition. IEEE, 2012, pp. 2392–2399.

[46].

K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, “Image denoising by sparse 3-d transform-domain collaborative filtering,” IEEE Transactions on image processing, vol. 16, no. 8, pp. 2080–2095, 2007.

[47].

K. Zhang, W. Zuo, Y. Chen, D. Meng, and L. Zhang, “Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising,” IEEE transactions on image processing, vol. 26, no. 7, pp. 3142–3155, 2017.

[48].

X. Mao, C. Shen, and Y.-B. Yang, “Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections,” Advances in neural information processing systems, vol. 29, pp. 2802–2810, 2016.

[49].

Y. Tai, J. Yang, X. Liu, and C. Xu, “Memnet: A persistent memory network for image restoration,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 4539–4547.

[50].

D. Liu, B. Wen, Y. Fan, C. C. Loy, and T. S. Huang, “Non-local recurrent network for image restoration,” arXiv preprint arXiv:1806.02919, 2018.

[51].

T. Plötz and S. Roth, “Neural nearest neighbors networks,” arXiv preprint arXiv:1810.12575, 2018.

[52].

S. Lefkimmiatis, “Universal denoising networks: a novel cnn architecture for image denoising,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 3204–3213.

[53].

K. Zhang, W. Zuo, and L. Zhang, “Ffdnet: Toward a fast and flexible solution for cnn-based image denoising,” IEEE Transactions on Image Processing, vol. 27, no. 9, pp. 4608–4622, 2018.

[54].

S. Guo, Z. Yan, K. Zhang, W. Zuo, and L. Zhang, “Toward convolutional blind denoising of real photographs,” in Proceedings of the IEEE/CVF Conference on Computer Visionand Pattern Recognition, 2019, pp. 1712–1722.

[55].

T. Brooks, B. Mildenhall, T. Xue, J. Chen, D. Sharlet, and J. T. Barron, “Unprocessing images for learned raw denoising,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019, pp. 11036–11045.

[56].

Y. Zhu and R. Bridson, “Animating sand as a fluid,” ACM Transactions on Graphics (TOG), vol. 24, no. 3, pp. 965–972, 2005.

[57].

R. Li and Y. Saad, “Gpu-accelerated preconditioned iterative linear solvers,” The Journal of Supercomputing, vol. 63, no. 2, pp. 443–466, 2013.

[58].

F. H. Harlow and J. E. Welch, “Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface,” The physics of fluids, vol. 8, no. 12, pp. 2182–2189, 1965.

[59].

N. Akinci, J. Cornelis, G. Akinci, and M. Teschner, “Coupling elastic solids with smoothed particle hydrodynamics fluids,” Computer Animation and Virtual Worlds, vol. 24, no. 3-4, pp. 195–203, 2013.

[60].

M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu, and X. Zheng, “TensorFlow: Large-scale machine learning on heterogeneous systems,” 2015, software available from tensorflow.org. [Online]. Available: http://tensorflow.org/

[61].

Z. Yue, H. Yong, Q. Zhao, L. Zhang, and D. Meng, “Variational denoising network: Toward blind noise modeling and removal,” arXiv preprint arXiv:1908.11314, 2019.

[62].

A. Frasson, T. A. Engel, and C. T. Pozzer, “Efficient screen-space rendering of vector features on virtual terrains,” in Proceedings of the ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, 2018, pp. 1–10.

[63].

M. Rapp and S. Spielmann, “Real-time hair rendering with screen space adaptive level of detail.”

<저자소개>

김 종 현

jkcgs-27-4-11-g16

2008년 세종대학교 컴퓨터학과 학사
2010년 고려대학교 컴퓨터학과 석사
2016년 고려대학교 컴퓨터학과 박사
2013년~2016년 (주)텐일레븐 선임연구원
2017년~현재 강남대학교 소프트웨어응용학부 부교수
관심분야 : 물리 기반 시뮬레이션, 가상/증강현실, 지오메트리 프로세싱, 게임 물리, 게임 AI