1. 서론
메쉬 분할(mesh segmentation)은 형상 검출(shape retrieval), 텍스 처 매핑(texture mapping) 그리고 메쉬 편집(mesh editing) 등 컴 퓨터 그래픽스의 다양한 응용 분야에서 활용되는 주요한 기술이 다. 이러한 응용에서 메쉬 특징 영역을 선택하는 것은 중요한 기 능적 요소이며, 이를 위해 다양한 기법이 제안되었다. 경계 분할 (boundary segmentation) 기법 [1]은 메쉬 분할의 대표적인 기법으 로 Hoffman과 Singh [2]의이론을 따라 분할 경계를 찾으며 비교 적 좋은 분할 결과를 보여주지만, 닫힌 경계선(closed boundary) 에 대한 보장이 없다. 닫힌 분할 경계선을 생성하기 위해 하모닉 필드를 이용한 기법 [3]이 제안되었다. 이는 특징 추출 가중치를 사용하는 라플라스 연산자와 포아송 방정식(Poisson equation)을 사용한다. 하모닉 필드를 이용한 기법은 메쉬의 노이즈에 민감하 지 않으며메쉬의자세 변화에 둔감하다는 장점이있다.
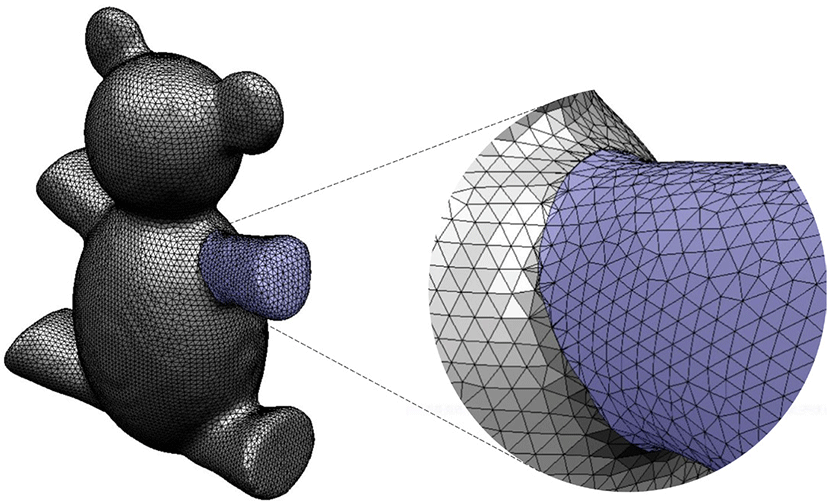
본 논문에서는 하모닉 필드를 이용한 메쉬 위의 특징 영역을 선택하고, 생성된 분할 경계에 대한 최적화 작업을 진행하여 부 드러운 분할 경계선을 생성하는 기법을 제안한다. 제안된 기법은 단일 클릭(single-click)을 이용한 새로운 방법의 사용자 인터페 이스로써 관심 있는 영역(region of interest)의 임의의 정점을 선 택해도 유사한 분할 결과를 보장한다는 점에서 기존 연구 [3, 4] 의 결과와 차이를 보인다. 그림 1은 제안된 기법을이용하여 선택 된 분할선을 보여준다. 관심 있는 영역을 Teddy 모델의 팔이라고 가정할 경우, 사용자가 팔 부분의 서로 다른 정점(파란색)을 선택 해도 생성된 분할선은 비슷한 결과를 나타낸다.

본 논문의 나머지 부분은 다음과같이 구성된다. 2장에서는 메 쉬 분할 기법에 관련된 기존 연구들에 대해서소개하고, 3장에서 는 하모닉 필드를 이용한 메쉬 분할 기법과 새로운 인터페이스인 3D Magic Wand 툴을 소개한다. 4장에서는 선택한 메쉬의 분할선 을 부드럽게 생성하기 위한 방법을 설명하고, 5장에서는 제안된 기법을 활용한 다양한 실험 결과를 보여준다. 끝으로 6장에서 본 논문의 결론과 향후 연구방향을 제시한다.
2. 관련 연구
본 장에서는 기존 메쉬 분할 방법에 대해 간단히 소개하고, 하모 닉 필드를 이용한 메쉬 분할과 관련된 주요 연구들에 대하여 소 개한다. 메쉬의 기하학적 특징을 이용한 영역 확장(region growing) 방법은 볼록 분할(convex decomposition) 알고리즘 [5]에서 착안된 기법으로 미리 정의된 조건(예: 볼록한 영역)을 만족하면 서 시드(seed) 정점이나 삼각형에서 시작하여 이웃 영역을 확장 해 나가는 방법이다. 유역 분할(watershed segmentation) 방법은 이미지 분할 및 분석 연구 [6]에서 제안된 알고리즘을 기반으로 Mangan 등 [7, 8]에 의해 처음 제안된 기법이다. 클러스터링(clustering) 방법은 k-평균 알고리즘 [9]을 기반으로 메쉬를 의미 있는 영역으로 분할하여 새로운 계층적 메쉬 분할을 제안하는 연구로 Katz와 Tal [10]이 제안하였다. 경계 분할 방법에는 곡률 기반 메 쉬 특징 경계 추출 기법 등이있다 [11, 12]. 이러한 기법은 사람의 시각에서 3차원 객체의 분할은 곡률의 최솟값에서 이루어진다는 Hoffman 등 [2, 13]의이론을 기반으로 제안되었다.
Zheng과 Tai [3]는 사용자가 메쉬 분할 부분에 하나 이상의 선 을 대략적으로 표현하는 인터페이스를 제안하였고, 이를 이용하 여 하모닉 필드의 등위선을 통한 메쉬 분할을 수행하였다. 추가 연구 [4]에서는 오목한 정보만을이용한 자동 메쉬 분할 알고리즘 을 제시하고 있으며, 오목한 부분의 영역을 고려한 하모닉 필드 를 생성하여 최적의 등위선을 선택하는 연구를 진행했다. 사용자 인터페이스인 Dot Scissor를 제안하는 연구 [14]에서는 사용자가 메쉬 분할 영역의 부분을 단일 클릭하는 인터페이스를 제안하 였다. 이 연구에서는 사용자의 입력을 분할이 이루어지는 경계 부분으로 제한하는단점이있다.
본 논문에서는 관심이있는 영역의 어떤 정점을 선택하더라도 자동으로 분할이 수행되는 인터페이스를 제안하며, 이러한 기술 에 있어서 기존 결과 [14]와 차이를 보인다. 일반적인 메쉬 분할에 대한 연구뿐만 아니라 치아 모델의 경계 선택을 위한 연구 분야 에서도 하모닉 필드를 사용한 분할 연구가 진행되고 있다. 치아 모델 같은 경우 임상 데이터마다 모양이 다르기 때문에 치아의 경 계를 인식하여 분할하는 것은 어려운 문제로 인식된다 [15, 16].
기존 대부분의 기법들은 분할 경계선을 매끄럽게 하기 위한 후처리 과정이 필요하다. 이는 실제로 생성된 경계선은 분할이 이루어질 부분보다 메쉬의 특성과 형상에 의존하는 경향이있기 때문이다. 따라서 본 논문에서는 기존 경계 부분의 메쉬의 특징 을 최대한 반영하면서 매끄러운 분할 경계선을 생성하는 방식을 제안한다.
3. 메쉬 특징 영역 선택 기법
하모닉 필드는 메쉬 위에서 정의된 특별한 스칼라 필드로 모 든 정점의 라플라스 값이 0을 만족한다. 메쉬 위에서 한 정점에 대한 라플라스는 메쉬 위의 스칼라 장이 정의되어 있다고 가정 을 했을 때, 주변 평균과의 차이로 정의된다. 라플라스 값이 0 을 만족하는 것은 각 정점의 함숫값이 주변 평균과 같다는 것을 의미한다. 정점(V), 에지(E), 삼각형(F )으로 정의되는 삼각 메 쉬 M = (V,E,F )에 대하여 정점 위에서 정의된 스칼라 함수를 f : V → R라고 할 때, f가 하모닉 필드가 되기 위해 ∆fi = 0 조건을이용한다 [17]. 이때 ∆는 라플라스 연산자(laplacian operator)이며 정점 pi에 대하여 다음과같이 정의된다:
여기서 wi,j는 차이에 대한 가중치이며, fi는 정점 pi의 함숫값 그리고 N1(i)는 pi의 1-링 이웃 정점의 집합이다. 이는 정점 pi의 값과 주변 평균의 차이를 나타내고 다음과같은 선형 시스템으로 계산될 수 있다:
여기서 L은 라플라스 행렬이며 L2와 b′는 하모닉 필드의 제약 조건(constraint)에 의해 정의된다. 이와 같은 선형 시스템을 계 산하여 메쉬 위의 하모닉 필드를 구할 수 있다. 그림 2(a)는 일 반적으로 사용되는 코탄젠트 가중치를 활용한 결과이며, 하모닉 필드가 부드럽게 생성이 되어 메쉬 위의 분할 영역에 대한 의미 있는 구별이 어려운 문제가 있다. 따라서 특징 영역에서 하모닉 필드의 값이 크게 변하는 필드를 생성해야 메쉬 분할에 활용을 할 수 있다.
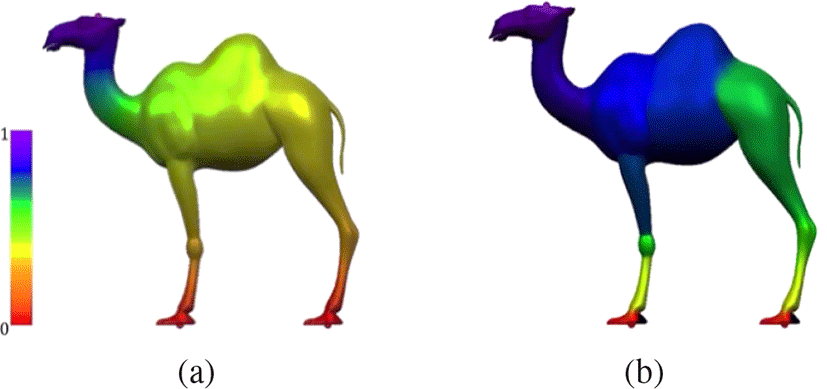
특징 영역에서 하모닉 필드의 값이 크게 변하는 필드를 생성 하기 위해 특징 추출 가중치를 활용한 하모닉 필드를 생성하고, 이를 이용하여 메쉬의 의미 있는 영역을 구별한다. 메쉬의 영역 에서 분할이 일어나는 부분은 최소 주곡률 방향으로 영역 간의 경계를 생성하고 오목한 주름(concave crease)에서 영역 분할이 이루어진다는 Hoffman의 결과 [2, 13]를 이용한다.
우선 오목한 영역의 정점들을 추출하고 오목한 영역의 정점들 과 연결된 에지의 가중치를 작은 값으로 설정한다. 상대적으로 작은 가중치로 연결된 두 정점은 하모닉 필드 생성 시, 이를 보 상(compensation) 하기 위해 큰 차이를 갖는 값이 할당된다. 이와 같이 하모닉 필드를 경계 부분에서 큰 차이를 갖도록 생성하는 원 리를 이용하여 메쉬를 분할한다. 오목한 영역의 정점을 검출하기 위한 식은 다음과같다:
여기서 ni는 정점 pi의 법선 벡터이고, p̂은 정점 pi의 주변 정점 들의 평균 위치를 나타낸다. 특징 추출을 위한 가중치는 다음과 같이 정의된다:
여기서 정점 pi와 pj가 연결이 되어있을 경우 γi,j를 곱하여 계산 하며 γi,j는 오목한 영역에 놓인 경우 상대적으로 작은 값인 0.01 을 할당하고 아닌 경우 1을 할당한다. 이때 |Ki|와 |Kj|는 두 정점 의 가우스 곡률이며 ||ei,j||는 에지의 길이이다. 그림 2(b)는 식 (4) 로 정의되는 가중치를 이용하여 하모닉 필드를 생성한 결과이다. 생성된 하모닉 필드에서 값의 크게 변화하는 부분을 조사하여 메 쉬의 분할 경계선을 찾을 수 있다.
3D Magic Wand 툴은 사용자 단일 클릭을 통해 메쉬의 특징 영 역을 선택하는 기법이다. 관심이 있는 영역의 임의의 점을 선택 한다는 부분에 있어서 기존의 특징 영역의 경계 부분을 선택하는 연구 결과 [14]와는 차이를 보인다. 그리고 3D Magic Wand 툴은 관심 있는 영역의 다른 점을 선택해도 동일한 선택 결과를 얻을 수 있다는 장점이 있다. 3D Magic Wand 툴의 선택 메커니즘은 다음과같다:
-
검사 영역 정의: 메쉬의 검사할 부분 영역은 사용자가 단일 클릭으로 하나의 정점을 선택한 후, 그 정점의 N-링 이웃 영역을 검사 영역으로 지정을 한다.
-
제약 정점의 결정 및 하모닉 필드 생성: 사용자가 선택한 정 점과 그 이웃 정점은 제약 정점으로 1값을 할당하고 N-링에 해당하는 영역의 경계 정점은 0값을 할당하여 하모닉 필드 를 생성한다.
-
하모닉 필드 분석을 통한 분할 경계선 결정: 생성된 하모닉 필드에서 샘플링된등위선들의 스코어를 정의하고, 가장 높 은 스코어를 갖는 등위선을 선택한다.
메쉬 전체에 대하여 조사하는 것은 시간 소요가 많아 비효율적 므로 메쉬의 검사 영역을 정의해야 한다. 검사 영역은 사용자가 선택한 하나의 정점으로부터 N-링 이웃 영역에 해당한다. N-링 은 사용자의 정의에 따라 다르며 마우스 스크롤을 통해 실시간 으로 제어할 수 있다. 이때 검사 영역의 크기는 선택하려는 특징 영역을 모두 포함해야 한다. 그림 3에서는 3D Magic Wand 툴의 N-링 조절을 통해 다양한 메쉬에서 검사 영역을 효율적으로 선 택할 수 있음을 보여준다.
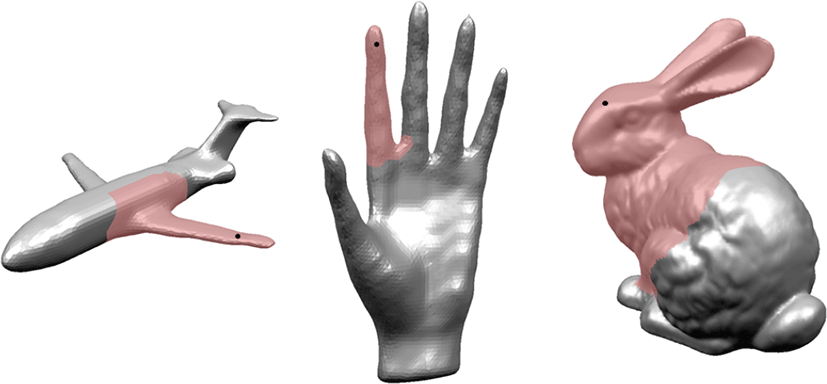
메쉬 위에서 하모닉 필드를 정의하기 위한 몇 가지 제약 조건을 설정하여 선형 시스템의 형태로 표현할 수 있다 [4, 14]. 검사 영역 이 정해진 후, 특징 추출을위한하모닉 필드 생성을위해서 제약 정점에 제약 조건을 할당한다(그림 4(a)). 이때 제약 조건으로 선 택된 정점과 주변 1-링 정점에 1값을 할당하고검사 영역의 경계 부분에 있는 정점들에 대하여 0값을 할당하여 하모닉 필드를 생 성한다. 특징 추출 가중치에 의해 오목한 영역, 즉 경계 부분에서 큰 차이를 보이는 하모닉 필드(그림 4(b))가 생성이 되고 하모닉 필드 값이 같은 등위선(그림 4(c))을 추출할 수 있다.

메쉬 특징 영역을 선택하기 위해 생성된 여러 가지 등위선 중 에서 최적의 분할 경계에 해당하는 등위선을 선택해야 한다. 이는 삼각형 내부에서 하모닉 필드의 그래디언트(gradient) 값을 이용 하여 선택할 수 있다 [4, 14]. 삼각형 내부의 그래디언트 값은 하 모닉 필드 변화율의 최대 방향이며 삼각형 내부에서 일정한 값을 가진다. 삼각형 T 의 그래디언트는다음과같이 계산된다:
여기서 fi는 정점의 하모닉 필드 값이고, ei⊥는 삼각형이 포함된 평면에서 에지의 수직한 방향 벡터이고, AT 는 삼각형의 면적을 나타낸다. 추출된등위선 Γi의 스코어 SΓi는다음과같이 정의된 다:
여기서 L(Γi)는 등위선 Γi의 길이, T 는 Γi와 교차하는 삼각형을 나타낸다. SΓi는 등위선 Γi에 대하여 단위 길이 당 등위선이 지나 가는 삼각형들의 그래디언트의 변화를 대표하는 값으로 생각할 수 있으며, 가장 높은 스코어를 선택하여 그 값에 대응되는 등위 선을 특징 분할 경계선으로 선택할 수 있다. 하지만 이렇게 선택 된 등위선은 부드럽지 못한 경계를 보이는 문제가 있다. 따라서 매끄러운 경계선 생성을위한 후처리 과정으로 선택된등위선이 지나는 삼각형의 스코어를 이용한 새로운 측지선을 생성하는 과 정을 수행한다.
4. 분할 경계 최적화
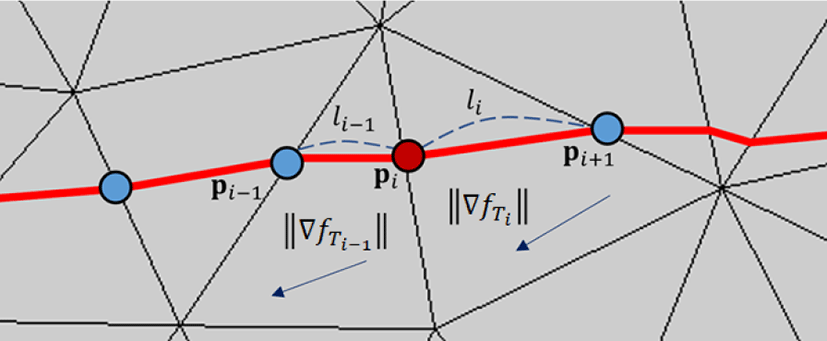
선택된 등위선을 부드럽게 만들기 위해서 분할 경계에 대해 최 적화를 수행한다. 최적화에 이용할 소수의 정점을 선택하기 위해 등위선 위의 정점마다다음과같은 스코어 값 Spi를 계산한다:
여기서 li−1은 정점 pi에서 이전 정점까지의 거리, li는 다음 정 점까지의 거리를 나타낸다(그림 5). 그리고 ||∇fTi−1||와 ||∇fTi|| 는 정점 pi을 공유한 양쪽 삼각형에서 계산된 하모닉 필드의 그 래디언트 크기이다. 이 값은 메쉬의 특징 영역과 관련이 있는 정 점에서 상대적으로 높은 스코어를 가지게 된다. 선택된등위선이 지나가는 각 정점마다 할당된 스코어 값을 기준으로 정점을 내 림차순으로 정렬한다. 스코어가 높은 정점들은 서로 가깝게 있기 때문에 높은 스코어의 정점만 선택하는 방법은 비효과적이다. 따 라서 정점들 사이의 일정 간격을 두어 필요한 정점만 선택하는 작업을 수행한다.
우선 스코어가 가장 높은 정점을 선택한다. 사용자가 원하는 소수의 정점의 개수를 k개라고 했을 때, 선택된 정점을 기준으로 등위선의 k개의 구간에서 가장 높은 스코어를 갖는 정점을 선 택한다. 구간별로 선택된 정점은 해당 구간에서 메쉬의 특징을 가장 잘 나타내는 정점이며, 이를 비등방 측지선으로 연결하여 분할 경계선을 생성한다.
메쉬 위의 측지선이 메쉬 특징을 따라 생성되도록 하기 위해 비 등방 거리 함수를 이용한다. 비등방 거리 함수는 최대 주곡률 방 향으로는 거리를 늘리고 최소 주곡률 방향으로 거리를 줄이는 원리를 가진다. 본 논문에서는 등위선에서 선택된 최적의 분할 경계점을 연결하는 비등방 측지선은 생성하고, 이를 최종 분할 경계선으로 사용한다.
비등방 거리 함수는 기존 연구 [18]에서 제안한 방법을이용하 여 계산한다. 메쉬 위의 각 정점 p의 접평면에서 거리 함수 gp는 다음과같이 표현된다:
여기서 v는 접평면에서 정의된 접벡터이고, 유클리드 거리 함수 인 경우 Mp가 단위행렬이 되며, 비등방 거리 함수의 경우 Mp는 다음과같이 표현될 수 있다:
여기서 e1은 최대 곡률을 갖는 주방향이고 e2는 최소 곡률을 갖는 주방향이고, Mp에 대한 고유값은 다음과같이 정의된다:
여기서 γ는 사용자가 정의한 상수로 논문 [18]에서는 0.01로 할당 을 했고 Sx는 |κ1|−|κ2|로 주곡률의 절댓값의 차이를 나타낸다. 이 값은 ridges와 valleys 부근일 경우 차이를 크게 보이며 평면에 가까울수록 0값에 수렴한다. 이러한 거리 함수를 이용하여 곡률 이 최대인 e1 방향으로 길이를 늘리고곡률이 최소인 e2 방향으로 길이를 줄일 수 있다.
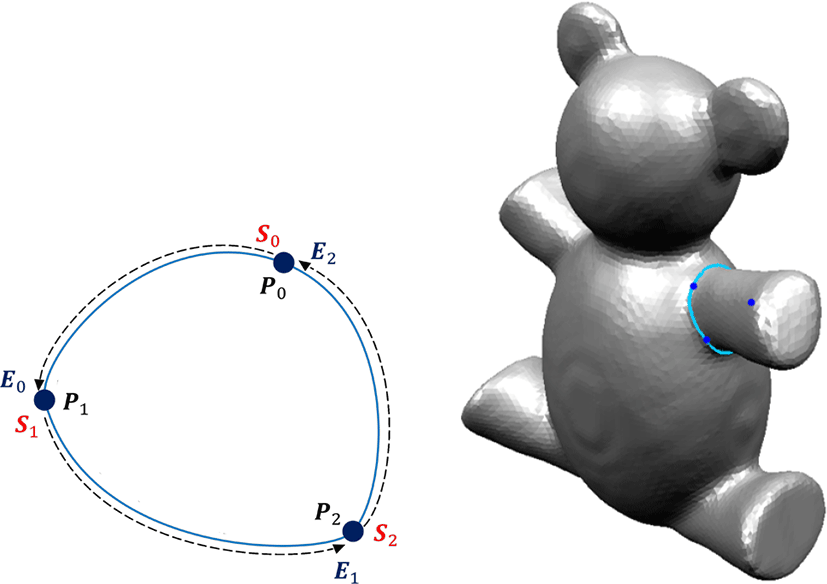
메쉬 위의 각 정점에 대해서 위와 같은 방법으로 생성된 비등 방 거리 함수를 이용하여 메쉬 에지 길이를 변경할 수 있다. 에지 길이는 에지의 두 정점에서 정의된 거리 함수의 평균을 사용한 다. 이는 실제 3차원 모델의 에지 길이가 변경되는 것은 아니고 내부적으로 변경된 에지 값을 가지고 있는 형태이다. 측지 경로 계산 알고리즘 [19, 20, 21, 22, 23]을 사용하여 변경된 에지 길이 를 갖는 메쉬 위에서 최적의 분할 경계점을 연결하는 닫힌 측지 선을 계산하여 부드러운 분할 경계선을 생성할 수 있다. 그림 6은 세 개의 분할 경계점(k = 3)을 연결하여 생성된 측지 경로(분할 경계선)을 나타내며, 그림 7은 k 값에 따른 결과의 차이가 크지 않다는 것을 보여준다. 따라서 본 논문에서는 기존 분할 결과의 특징을 반영하면서 비등방 측지선을 효율적으로 계산하기 위해 최소한의 정점으로 k의 개수를 3으로 설정했다.
5. 실험 결과
본 논문에서 제안된 3D Magic Wand 메쉬 분할 기법은 C++ 언 어를 사용하여 구현하였으며, 모든 실험은 Intel Core i5-10400 Processor 2.90GHz CPU, 16GB 메모리와 NVIDIA GeForce GTX 1650 GPU가 설치된 PC 환경에서 수행되었다. 다양한 실험의 렌 더링 결과는 OpenGL을 기반으로 구현하였으며, 삼각 메쉬를 효 과적으로 표현하기 위해 하프 에지(halfedge) 자료구조를 이용하 였다.
본 논문에서 제안하고 있는 인터페이스인 3D Magic Wand 툴과 기존 연구의 Dot Scissor [14]에 대하여 비교 실험을 진행하였다. Dot Scissor는 메쉬 분할을 위한 기법으로 하모닉 필드를 활용 하고 사용자의 인터페이스로 단일 클릭 방법을 사용한다는 점에 서 본 논문의 3D Magic Wand 툴과 유사한 인터페이스이다. Dot Scissor 이후 하모닉 필드를 이용한 스케치 기반 인터페이스 연 구 [24]가 있었지만, 인터페이스 기법이 본 논문에서 제안한 방 법과 차이를 보였다. 따라서 Dot Scissor와 비교 실험을 통해 3D Magic Wand 툴의 일관성 있는 결과를 보여주었다. Dot Scissor 는 선택한 정점으로부터 일정한 거리에 있는 8개의 제약 정점을 사용하여 하모닉 필드를 만들고 제약 정점 사이의 분할 경계선 중에서 최종 분할 경계선을 선택한다. 따라서 선택한 정점이 메 쉬의 분할이 이루어지는 부분이나 근처에 있을 경우에만 메쉬 분할 경계선이의미 있게 생성되었다. 그림 7은 Bunny 모델의 머 리 영역을 각각의인터페이스로 선택한 비교 결과이다. 그림 8(a) 와 8(b)는 Dot Scissor의 결과로 초록색 분할 경계선을 생성하였 고, 그림 8(c)와 8(d)는 3D Magic Wand 툴의 결과로 파란색 분할 경계선을 생성하였다. 그림 8(a)에서는 선택한 정점이 분할 영역 근처에 있었지만, 그림 8(b)처럼 분할 영역이 아닌 임의의 정점을 선택할 경우 의도와 다른 분할 경계선이 생성되었다. 이에 비해 3D Magic Wand 툴은 그림 8(c)와 8(d)처럼 메쉬 분할 영역 내의 어느 부분을 선택해도 분할 경계선이 안정적으로 잘 생성되는 것 을 볼 수 있다. 이는 사용자가 메쉬 분할을 위해 더욱 간편하고 직관적인인터페이스를 이용할 수 있다는 이점을 보여준다.
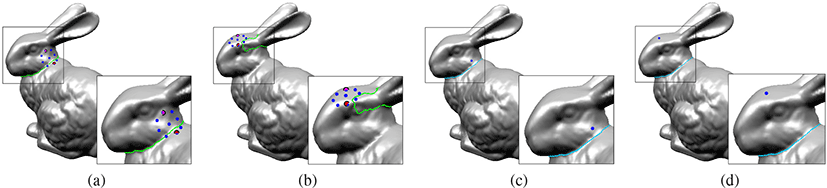
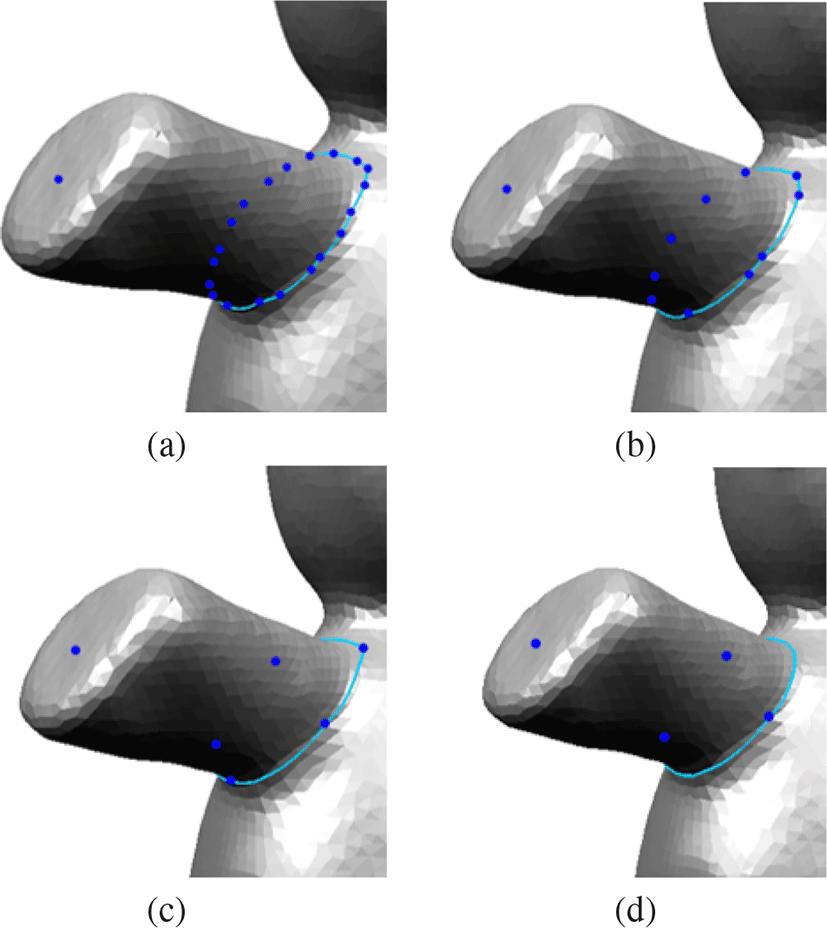
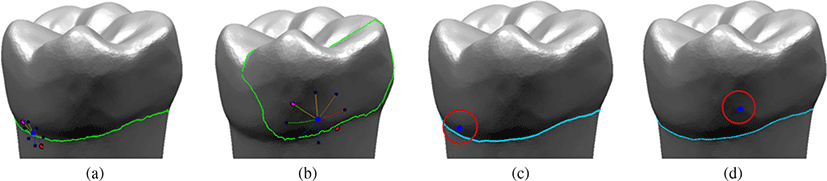
그림 9는 치아 모델을이용하여 치관과 치근 영역 사이의 분할 경계를 선택한 비교 결과이다. 그림 8와 마찬가지로 Dot Scissor 는 초록색 분할 경계선을 사용하였고, 3D Magic Wand 툴은 파 란색 분할 경계선을 사용하였다. Dot Scissor는 그림 9(a)처럼 선 택한 정점이 분할 영역 근처에 있는 경우 의미 있는 분할 결과를 보였다. 하지만 메쉬 표면이 울퉁불퉁한 특성이 있는 경우 불안 정한 결과를 보였다. 그림 9(b)처럼 그림 9(a) Dot Scissor의 영역 을 2배로 넓혀 분할 경계 영역을 포함하더라도 울퉁불퉁한 메쉬 표면의 특성에 따라 분할 경계선이 생성되었다. 3D Magic Wand 툴은 그림 9(c)와 9(d)의 빨간색 원으로 표시한 Dot Scissor와 같은 정점뿐만 아니라 다른 임의의 정점을 선택해도동일한 결과를 보 여주었다. 이는 울퉁불퉁한 메쉬 표면에서 정점을 선택하더라도 의미 있는 메쉬 분할 경계선이 생성된다는 것을 보여준다. 또한 3D Magic Wand 툴은 메쉬 분할을 위한 특징 추출 하모닉 필드 생성 시, 메쉬 전체에 대해 연산을 수행하지 않고 지정된 특정 영 역만을 계산하기 때문에 메쉬 특징 영역 검사에 있어서 효율적인 성능을 보여준다.
분할 경계 최적화 기법을 통해 선택된 등위선으로부터 부드러 운 경계선을 생성할 수 있다. 그림 10은 선택된 등위선과 비등방 측지선으로 개선된 경계를 나타낸다. 그림 10(a)와 같이 파란색 정점을 기준으로 메쉬 특징 영역을 포함하는 검사 영역(분홍색 영역)에 대하여 10(b)의 개선된 분할 경계선(파란색)과 10(c)의 초기 등위선(빨간색)을 생성하였다. 선택된 등위선과 비교하였 을 때 개선된 분할 경계선(파란색)이 더 나은 결과를 보여준다.
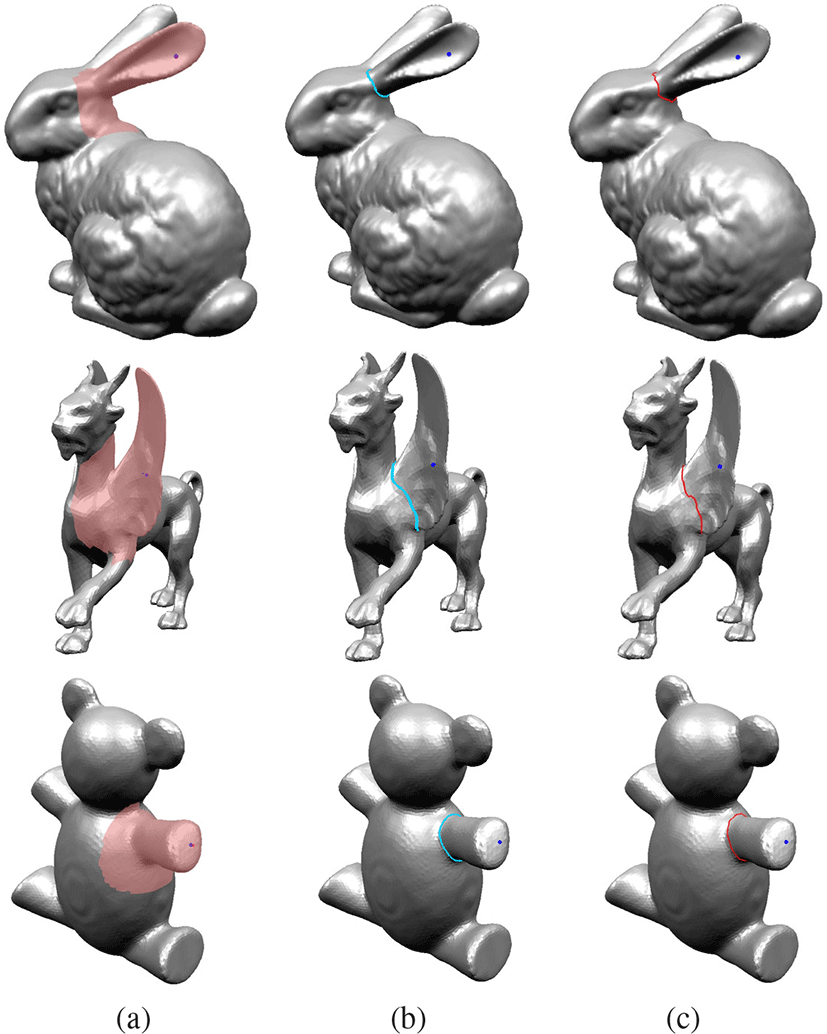
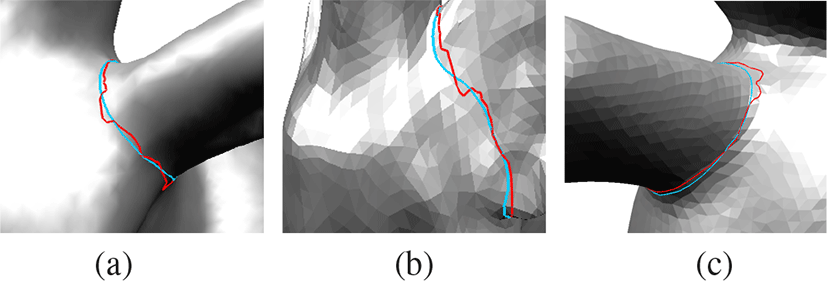
그림 11는 초기 등위선(빨간색)과개선된 경계선(파란색)의 비 교 결과를 나타낸다. 초기 등위선은 메쉬의 형상에 따라 울퉁불 퉁하게 생성되었지만, 비등방 측지선을이용한 분할 경계선은 메 쉬의 특징을 따라 부드럽게 생성되었다. 기존의 Yang 등 [25]의 치아 모델 분할 연구는 개선한 비등방 측지선을이용한 3D Intelligent Scissors를 제안하였다. 이는 기존의 비등방 측지선 [18]의 인터페이스와 동일한 형태이며 비등방 측지선의 부드러움의 강 도를 조절하여 메쉬 분할을 수행하였다. 본 논문의 개선된 분할 경계선은 Yang과 Wang의 개선한 비등방 측지선과 유사한 연구 결과를 보여주며 비교적 직관적인인터페이스를 통해 더욱 간단 한 선택이 가능하다. 그림 12은 개선된 분할 경계선을 활용하여 경계 부분을 따라 특징 영역을 부드럽고 자연스럽게 선택한 결과 를 나타낸다.
6. 결론
본 논문에서는 특징 추출 하모닉 필드를 이용한 메쉬 특징 영역 선택을 지원하는 새로운 사용자 인터페이스인 3D Magic Wand 툴을 제안하였다. 3D Magic Wand 툴을이용하여 관심이있는 영 역의 어떠한 정점을 선택하더라도 비슷한 메쉬 특징 영역이 선택 되는 결과를 보였다. 또한 선택된 메쉬 영역의 분할 경계에 대한 후처리 과정을 진행하여 기존보다 매끄러운 경계선을 생성할 수 있는 방법을 제안하였다. 생성한 메쉬 분할 경계선을 이용하여 메쉬 분할, 텍스처 할당, 형상 검출 등 다양한 응용 분야에 활용할 수 있을 것이라 기대한다.
본 논문에서 새로운 인터페이스를 사용하여 메쉬 분할이 효율 적으로 수행된다는 것을 다양한 실험 결과를 통해 알 수 있었지 만, 제안 방법은 현재 사용자의 단일 클릭을 통해 처음 선택된 영역에서 메쉬 분할이 수행되고 있다. 기존 선택한 검사 영역을 확장하고 축소할 수 있는 기능에 대한 추가적인 연구가 필요하다. 또한 인터페이스에 기반이 되는 특징 추출 하모닉 필드에 대한 추 가적인 연구가 필요하다. 하모닉 필드 생성 시에 메쉬의 특징을 추출할 수 있는 기법들은 기존 연구들을 바탕으로 수행되었다. 향후 연구에서는 인터페이스 추가 연구와 하모닉 필드에 필요한 메쉬의 오목성 판단 및 특징 추출 가중치에 대한 추가 연구를 진 행할 예정이다.