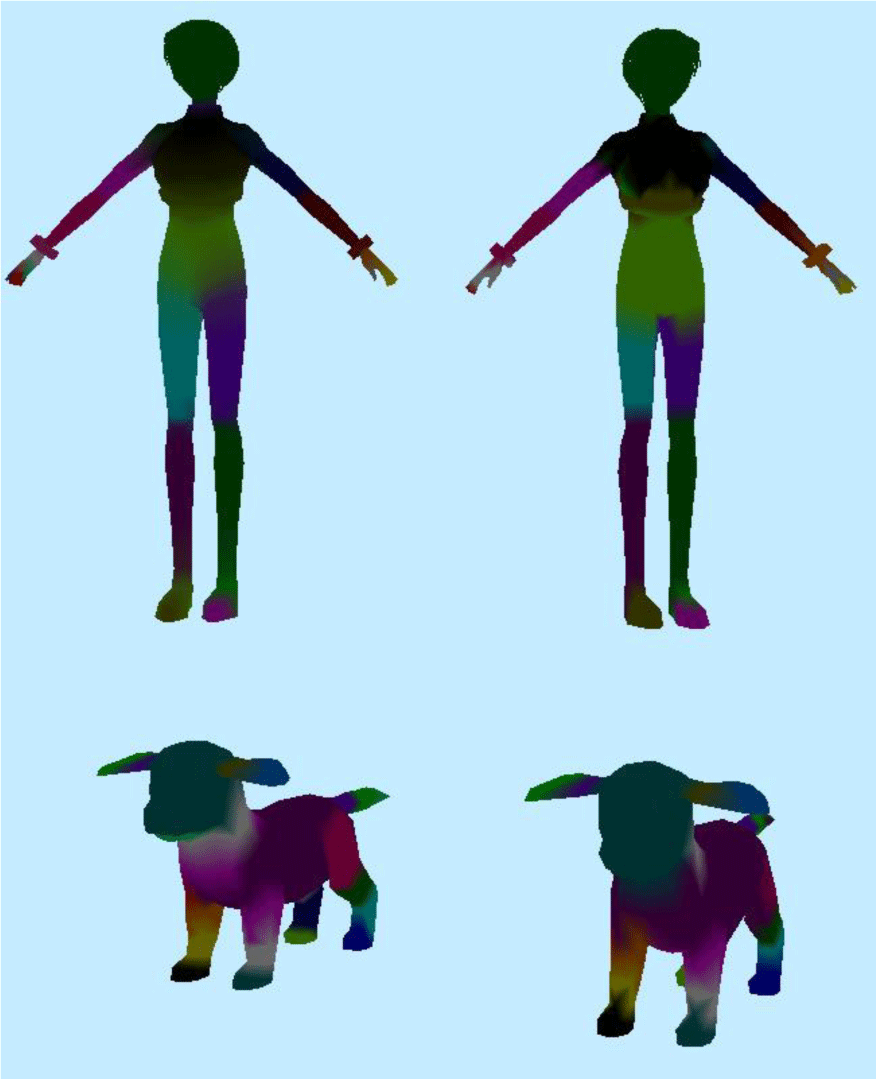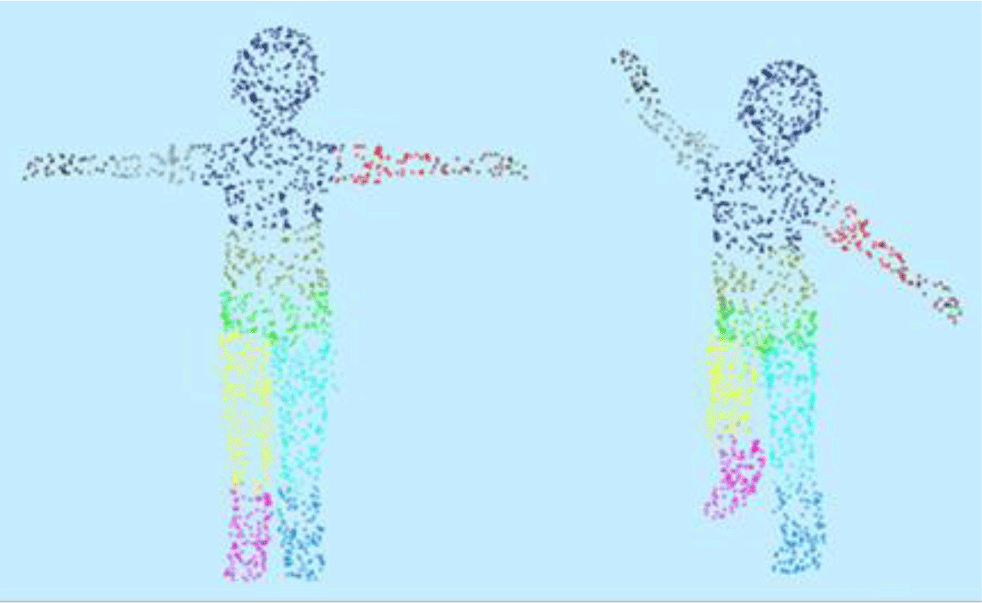Article
SDF를 이용한 자동 스키닝 웨이트 페인팅 신경망
설효석
1
, 권태수
1,*
Neural network for automatic skinning weight painting using SDF
Hyoseok Seol
1
, Taesoo Kwon
1,*
1Dept. of Computer and Software, Hanyang University
*corresponding author: Taesoo Kwon / Department of Computer Science, Hanyang University Graduate School (
taesoobear@gmail.com)
© Copyright 2023 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Jun 29, 2023; Revised: Jul 30, 2023; Accepted: Aug 16, 2023
Published Online: Sep 01, 2023
요약
컴퓨터 그래픽스 및 컴퓨터 비전 분야의 발전에 따라 삼차원 물체를 다양한 표현 방식으로 나타내고 있다. 이에 따라 여러 표현 방식을 사용하는 캐릭터의 애니메이션 제작에 대한 수요 또한 증가하고 있다. 캐릭터 애니메이션 제작에 주로 사용되는 스켈레탈 애니메이션의 경우 캐릭터 표면이 어느 관절로부터 영향을 받는지를 정하는 스키닝 웨이트 페인팅 작업이 필요하다. 본 논문은 삼각형 메시를 비롯한 여러 표현방식으로 나타난 캐릭터에 대한 스키닝 웨이트 페인팅 과정을 자동화하는 방법을 제안한다. 우선 다양한 표현 방식을 사용한 삼차원 캐릭터에 대해 일반적으로 사용할 수 있도록 Signed Distance Field(SDF)를 이용한다. 이후 그래프 신경망과 다층 퍼셉트론 계층 구조를 활용하여 캐릭터 표면 상에 주어진 위치에서의 스키닝 웨이트를 예측할 수 있다.
Abstract
In computer graphics and computer vision research and its applications, various representations of 3D objects, such as point clouds, voxels, or triangular meshes, are used depending on the purpose. The need for animating characters using these representations is also growing. In a typical animation pipeline called skeletal animation, "skinning weight painting" is required to determine how joints influence a vertex on the character's skin. In this paper, we introduce a neural network for automatically performing skinning weight painting for characters represented in various formats. We utilize signed distance fields (SDF) to handle different representations and employ graph neural networks and multi-layer perceptrons to predict the skinning weights for a given point.
Keywords: 스키닝 웨이트; 리깅 자동화; 그래프 신경망; 3D애니메이션
Keywords: Skinning Weight; Automatic Rigging; Graph Neural Network; 3D Animation
1. 서론
컴퓨터 그래픽스, 컴퓨터 비전 분야의 연구와 그 활용에 있어서 삼차원 물체는 활용 목표에 맞추어 포인트 클라우드, 복셀, 삼각형 메시 등 다양한 표현 방식을 사용한다. 그리고 영화, 게임, 소셜미디어 등의 영역에서 사용하는 기술들의 발전에 따른 다양한 방식으로 표현된 캐릭터의 애니메이션 제작 기술의 요구도 증가하고 있다.
게임 제작 시 주로 이용하거나 일반적인 3D 모델링 툴에서 제공하는 3D 캐릭터 애니메이션 제작방식인 스켈레탈 애니메이션은 크게 두 단계로 이루어져 있다. 먼저 애니메이터가 관절로 이어진 자세를 나타낼 수 있는 캐릭터의 뼈대, 즉 스켈레톤을 만든다. 애니메이터는 이 스켈레톤의 각 관절에 적당한 회전을 적용하여 자세를 만들어 낼 수 있다. 이후 캐릭터 메시 모델과 스켈레톤을 엮는다. 캐릭터 메시 표면의 특정 점이 뼈에 영향을 받는 정도를 "스키닝 웨이트 (Skinning Weight)"라고 한다. 스키닝 웨이트를 정하는 과정은 애니메이터가 직접 스켈레톤의 한 뼈를 고르고, 그 뼈의 영향을 받는 부분을 캐릭터에 칠하는 방식으로 이 단계를 수행하기 때문에, 이 과정을 "스키닝 웨이트 페인팅 (Skinning Weight Painting)"이라고 한다. 이 두 단계가 끝나면, LBS[1]나 DQS[2]와 같은 알고리즘을 통해 스켈레톤의 자세에 따라서 캐릭터의 모양이 어떻게 변형되는지 계산할 수 있다. 애니메이터는 프레임별로 스켈레톤의 자세를 만드는 것으로 캐릭터의 애니메이션을 만들 수 있게 된다.
스키닝 웨이트 페인팅 과정은 숙련된 애니메이터가 필요하고, 시간도 오래 걸리므로 이를 자동화하는 연구들[3-9]이 많이 이루어졌다. 스켈레탈 애니메이션은 캐릭터 각 위치의 변형을 계산할 수 있어 다른 표현 방식으로 나타낸 캐릭터에도 적용할 수 있으나, 이러한 연구들은 대부분 삼각형 메시 캐릭터에 적용하는 방법으로 이루어져 왔다.
본 논문은 임의의 표현 방식으로 나타낸 캐릭터상의 한 점의 스키닝 웨이트를 예측하는 것을 목표로 한다. 이를 위해 3D 캐릭터를 암묵적(implicit)으로 나타낼 수 있는 Signed Distance Field (SDF) 그리드를 만든다. 어 위치로부터 3D 캐릭터의 표면 사이의 거리를 절댓값으로 하고 그 위치가 캐릭터 내부인 경우에는 음수, 외부인 경우에는 양수로 부호를 정한 값을 그 위치의 Signed Distance라고 한다. SDF는 Signed Distance를 각 위치에 저장한 것이다. SDF와 같은 암묵적인 표현 방식들은 삼차원 물체의 학습 가능한 표현 방식으로써 좋은 결과를 보여주었기에 본 논문에서 스키닝 웨이트 예측을 위한 물체 모양 학습으로 SDF를 이용하였다.
따라서 본 논문에서는 이 SDF를 활용하여 스키닝 웨이트 예측을 수행하는 신경망 (Neural Network)을 구축하였다. SDF 그리드의 오토인코더 (Auto-encoder)를 만들어 그로부터 압축된 모양 정보를 얻어내고, 이 정보와 스켈레톤, 그리고 스키닝 웨이트를 예측하고자 하는 위치를 신경망의 입력으로 받으면 그 지점의 스키닝 웨이트를 출력한다. 2장에서는 본 연구와 관련된 기존 연구를 살펴본다. 3장에서는 구축한 신경망의 구성에 관해 설명한다. 이후 4장에서 스키닝 웨이트 실험 결과를 확인하고, 5장에서 한계점과 추후 연구 방향에 대하여 서술한다.
2. 관련 연구
2.1 스키닝 웨이트 페인팅 자동화
스키닝 웨이트 페인팅 자동화에 대한 기술들은 크게 기하학 기반 (geometric-based) 방법과 데이터 중심 (data-driven) 방법 두 가지로 나눌 수 있다.
기하학 기반 방법은 캐릭터와 스켈레톤 사이의 기하학적인 관계를 이용한다. 스키닝 웨이트 페인팅 자동화에 대한 초기 연구들이 주로 이 방법을 사용하였다. 이 방법은 관절과의 거리가 스키닝 웨이트에 큰 영향을 미친다고 가정한다. 따라서 Heat diffusion[3], illumination model[4], Laplacian energy[5], geodesic voxel binding[6] 등 다양한 방법으로 관절까지의 거리를 계산하여 스키닝 웨이트를 예측하였다.
인공지능과 기계학습 기술의 발전에 따라서 데이터 중심 방법으로 스키닝 웨이트 페인팅을 수행하는 연구도 진행됐다. SNARF[10], Neural Blend Shape[11] 등에서, 모션 캡처 데이터를 활용하여 스키닝 정보를 나타내는 심층 신경망 구조를 학습해 스켈레톤의 변형을 캐릭터의 스킨에 적용하는 과정을 보여주었다. 이 방식은 학습에 사용한 데이터와 같은 인간 형태의 스켈레톤 구조를 가진 캐릭터에서 훌륭한 결과를 보여줬다. 그러나 모션 캡처 데이터에 사용한 스켈레톤과 다른 구조를 갖는 캐릭터에는 적용할 수 없다는 한계가 있다.
다양한 구조를 가진 캐릭터와 스켈레톤에 대해서 적용 가능한 데이터 중심 방법으로 NeuroSkinning[7], RigNet[8], SkinningNet[9] 등 그래프 신경망을 활용한 방법이 제안되었다. 스켈레톤의 경우에는 관절을 노드로 뼈를 엣지로 변환하고, 삼각형 메시 캐릭터는 꼭짓점을 노드로 변을 엣지로 변환하는 방법으로 스켈레톤과 캐릭터로부터 그래프를 만들어 낸다. 이렇게 변환한 그래프를 그래프 신경망의 입력으로 하여 좋은 결과를 얻어내었다. 그러나 이 방법들은 그래프로 변환이 쉬운 삼각형 메시에서만 적용이 가능하다.
2.2 그래프 신경망
본 논문에서는 캐릭터에 대응하는 스켈레톤의 정보를 구하고, 스켈레톤의 각 관절이 갖는 특성 벡터를 얻기 위하여 그래프 신경망을 이용하였다.
그래프 신경망(Graph Neural Network, GNN)[12]은 합성곱 신경망 (Convolutional Neural Network)을 그래프 자료구조에 적용하기 위한 방법으로 처음 제안되었다. 이후 GNN에 대한 연구가 지속되었고, 현재 GNN은 크게 스펙트럼 접근방식(spectral approach) [13, 14]과 공간적 접근방식(spatial app-roach)[15-17]으로 나눌 수 있다.
그래프 신경망에 대한 최근의 연구들은 대부분 공간적 접근방식을 일반화한 메시지 전달(Message-Passing) 방법[18]을 적용하고 있다. 그래프 합성곱 신경망 (Graph Convolutional Net-work, GCN)[16]은 메시지 전달을 구현한 방법의 하나로, 이웃한 노드의 수에 따라 정규화한 가중치 행렬을 사용하여 노드의 특징 벡터를 변환하는 방법을 제안한다.
EdgeConv[19]도 메시지 전달 방법의 그래프 신경망 중 하나로, 삼차원상에서 기하학적인 특성을 그래프의 엣지를 통해 전달하도록 하였다. 신경망의 각 단계마다 이웃한 노드로부터의 정보를 다층 퍼셉트론(Multi-Layer Perceptron, MLP)에 입력하여 그 결과로 노드를 업데이트하는 방식으로 신경망을 학습한다. 본 논문에서 관절의 특성 벡터를 얻기 위한 방법으로 메시지 전달 방식의 GNN인 EdgeConv 방식을 활용하였다.
2.3 SDF를 이용한 삼차원 물체 모양 학습
Signed Distance Field(SDF)란, 각 지점의 값이 삼차원 물체의 표면까지의 거리를 절댓값으로 갖고, 그 위치가 물체의 내부인 경우 음수, 외부인 경우 양수로 부호를 갖는 영역을 통해 삼차원 물체를 암묵적으로 표현하는 방법이다.
이 SDF 그리드를 이용하여 삼차원 물체를 학습하는 연구도 많이 행해졌다. Shape Descriptor를 학습하거나[20], 3D Shape com-pletion을 수행[21, 22] 하는 등의 연구에서 삼차원 물체의 모양을 SDF 그리드를 활용하여 학습하는 것을 보여주었다. SDF로 나타낸 캐릭터의 변형을 학습하여 변형된 캐릭터를 재구축하는 연구도 진행되었다[23]. 이러한 연구들은 대부분 SDF 그리드에 3D CNN을 적용하여 삼차원 물체의 모양을 학습하였다. 본 논문에서도 캐릭터의 모양을 학습하기 위하여 SDF그리드를 입력으로 하는 3D CNN을 사용하였다.
3. 방법
본 연구에서는 1×1×1 크기로 정규화된 캐릭터의 SDF 그리드와 그 캐릭터에 대응하는 스켈레톤, 스키닝 웨이트를 구할 지점의 위치 좌표를 입력으로 받아 해당 지점의 스키닝 웨이트를 얻는 신경망을 제안한다. 이 과정은 크게 네 단계로 이루어진다. 먼저 SDF 오토인코더를 이용하여 캐릭터 모양 정보를 인코딩하고, 메시지 전달 방식의 GNN을 이용하여 스켈레톤의 각 관절의 특성 벡터를 구한다. 이후 주어진 지점의 좌표와 캐릭터 모양 정보를 이용하여 지역 특성을 계산하고, 최종적으로 스키닝 웨이트를 예측한다.
3.1 SDF 오토인코더
스키닝 웨이트 예측 신경망을 학습하기에 앞서, 캐릭터의 모양 정보를 얻기 위하여 SDF 오토인코더를 사전 학습한다. 먼저 캐릭터를 1×1×1 크기로 정규화한 후 그 캐릭터 위에 r×r×r 해상도의 그리드를 설정한다. 각 그리드에는 해당 칸의 중심 위치의 SDF 값을 갖도록 한다. 이렇게 만든 그리드 X ∈ Rr3 를 SDF 오토인코더의 레이어의 입력으로 한다.
SDF 오토인코더는 인코더 부분과 디코더 부분으로 나누어진다. 인코더는 삼차원 합성곱 계층(3D convolutional layer)과 풀링 계층(pooling layer)으로 이루어져 SDF를 256차원의 잠재 벡터(latent vector) Y ∈ ℝdmesh 로 변환한다. 디코더는 Y를 다시 SDF 그리드로 복원하는 역할을 하기 위하여 여러 개의 삼차원 합성곱 계층과 전치 합성곱 계층(transposed convolutional layer)로 이루어져 있다. 이 네트워크의 자세한 정보는 Table 2에 있다.
이후 복원한 SDF그리드 (X̂) 과 원본 SDF 그리드 데이터를 가지고 아래 식과 같은 평균 제곱 오차(mean squared error, MSE) 손실 함수를 이용하여 오토인코더를 학습한다.
이 단계에서 얻은 잠재 벡터 Y를 이후 단계에서 캐릭터 모양의 특징으로 사용한다.
3.2 스켈레톤 네트워크
이 단계에서는 주어진 스켈레톤의 각 관절의 특성 벡터를 계산한다. 먼저 스켈레톤의 각 관절을 꼭짓점으로 하고 관절을 연결하는 뼈를 변으로 하는 무방향 그래프 G = (V,E)를 만든다. 꼭짓점 v ∈ V는 관절의 위치 정보 벡터 xv를 가진다. xv는 삼차원 좌표를 NeRF[24]에서와 같이 아래 매핑 함수 γ를 이용하여 2L·3 차원으로 늘린 벡터이다.
스켈레톤을 그래프 자료구조로 변환하였으면 해당 그래프를 입력으로 하는 GNN을 만든다. 본 논문에서는 메시지 전달 방식을 이용한 그래프 신경망 중 EdgeConv[19]을 활용하였다. 본 논문에서 EdgeConv의 변 특성(edge features)을 구하는 학습 가능한 비선형 함수로는 MLP를 사용하였고, 변 특성의 aggregation에는 평균 함수를 이용하였다. xv가 EdgeConv 계층 하나를 지나며 xv'로 업데이트되는 과정을 정리한 식은 아래와 같다.
여기서 N(v)는 v에 인접한 꼭짓점의 집합이다. 스켈레톤 네트워크에서 각 관절은 두 개의 EdgeConv 계층을 통해 dskel차원의 특성 벡터를 가지게 된다.
3.3 지역 특성 네트워크
주어진 위치의 스키닝 웨이트를 예측하기 전에 주어진 점이 캐릭터 모양 내에서 어떤 지역적인 정보를 가지고 있는지를 생성하기 위해 지역 특성 네트워크 단계를 거친다. 이때 3.2절에서와 마찬가지로 해당 위치의 좌표 p를 매핑 함수 γ를 이용하여 더 높은 차원으로 만들고, 3.1절의 오토인코더에서 얻은 캐릭터의 잠재 벡터 Y와 연결(concatenate)한다. 위치 정보와 캐릭터 정보를 연결한 벡터를 입력으로 하는 MLP를 거쳐 해당 위치의 모양에 대한 dlocal차원의 정보 xlocal을 얻는다. 이 과정을 정리하면 아래 식과 같다.
3.4 스키닝 웨이트 예측
지역 특성 네트워크에서 얻은 결과와 스켈레톤 네트워크에서 얻은 각 관절의 특성 벡터를 이용하여 최종적으로 스키닝 웨이트를 예측한다. 이때 예측 신경망에 입력하는 크기를 고정하고, 좀 더 효율적인 계산을 위하여 k-최근접 접근 방식(k-Nearest Neighborhood approach)을 이용해 스키닝 웨이트를 예측할 지점과 가까운 k개의 관절에 대한 스키닝 웨이트를 예측한다. 점과 관절 사이의 거리는 Dionne[6]의 방법에서 사용했던 것처럼 SDF 그리드 안에서 캐릭터의 내부에 존재하는, 즉, 음수인 값을 가지는 위치를 복셀로 만들고 연결된 복셀의 측지 거리(geodesic distance)를 이용하였다.
스키닝 웨이트 예측 신경망의 결과는 스키닝 웨이트의 특성을 유지하기 위하여 소프트맥스 활성 함수(softmax activation function)를 이용하여 각 값이 0 이상 1 이하가 되고 값의 합이 1이 되도록 만든다. 최종적으로 입력 지점 p에서 예측한 스키닝 웨이트 는 다음과 같다.
는 p에서 i번째로 가까운 관절의 특성 벡터이다. 이렇게 구한 결과를 이용하여 스켈레톤 네트워크, 지역 특성 네트워크, 스키닝 웨이트 예측 네트워크를 학습하기 위하여 아래 식의 크로스 엔트로피 손실 함수를 이용하였다.
4. 구현 및 결과
본 논문에서 제안한 방법은 RigNetv1[8] 데이터셋으로 PyTorch[25]와 PyTorch Geometric[26]을 사용하여 전체 네트워크 학습을 진행하였다. RigNetv1 원본 데이터셋은 총 2703개의 리깅이 완료된 삼각형 메시 캐릭터로 이루어져 있고, 학습을 위하여 각 캐릭터 메시는 1 × 1 × 1 크기에 맞춰 정규화 한 후 SDF 그리드로 변환하였다. 본 논문에서 사용한 신경망의 세부 정보는 Table 1과 같다.
Table 1:
Detailed Information of Our Networks
|
SDF 오토인코더 |
|
SDF 해상도 (r) |
64 |
|
dmesh
|
256 |
|
스켈레톤 네트워크 |
|
매핑 차원 (L) |
5 |
|
EdgeConv 계층 수 |
2 |
|
은닉 계층 차원 |
128 |
|
dskel
|
256 |
|
지역 특성 네트워크 |
|
매핑 차원 (L) |
10 |
|
은닉 계층 차원 |
256 |
|
dlocal
|
256 |
|
스키닝 웨이트 예측 네트워크 |
|
최근접 관절 수 (k) |
5 |
|
은닉 계층 차원 |
256, 128 |
Download Excel Table
4.1 SDF 오토인코더 구현 및 결과
SDF 오토인코더의 인코더 및 디코더 세부 구현은 Table 2와 같다. conv는 3D 합성곱 계층, pooling은 풀링 계층, fc는 완전 연결 계층(fully-connected layer), deconv는 전치 합성곱 계층을 의미하고, 괄호 안의 숫자는 각 계층의 입출력 차원을, 아래는 전체의 입력과 출력 차원을 의미한다.
Table 2:
Detailed Information of SDF Autoencoder
|
Encoder |
|
Layer 1 |
conv(1, 32) + conv(32, 32) + pooling
(64 × 64 × 64 × 1 → 32 × 32 × 32 × 32) |
|
Layer 2 |
conv(32, 64) + conv(64, 64) + pooling
(32 × 32 × 32 × 32 → 16 × 16 × 16 × 64) |
|
Layer 3 |
conv(64, 128) + conv(128, 128) + pooling
(16 × 16 × 16 × 64 → 8 × 8 × 8 × 128) |
|
Layer 4 |
conv(128, 128) + conv(128, 128) + fc(65536, 256) + fc(256, 256)
(8 × 8 × 8 × 128 → 256) |
|
Decoder |
|
Layer 1 |
fc(256, 256) + fc(256, 65536) + conv(128, 128) + conv(128, 128)
(256 → 8 × 8 × 8 × 128) |
|
Layer 2 |
deconv(128, 128) + conv(128, 128) + conv(128, 64)
(8 × 8 × 8 × 128 → 16 × 16 × 16 × 64) |
|
Layer 3 |
deconv(64, 64) + conv(64, 64) + conv(64, 32)
(16 × 16 × 16 × 64 → 32 × 32 × 32 × 32) |
|
Layer 4 |
deconv(32, 32) + conv(32, 32) + conv(32, 1)
(32 × 32 × 32 × 32 → 64 × 64 × 64 × 1) |
Download Excel Table
오토인코더 학습에는 데이터의 90%를 훈련에 사용하고 10%를 평가 및 검증에 사용하였다. 0.0001의 학습률로 총 1000에포크 동안 진행하였고, 약 40시간이 걸렸다. Figure 1은 이 오토인코더를 이용하여 SDF 그리드를 재구축한 모습을 나타낸다.
4.2 스키닝 웨이트 페인팅 결과
본 논문에서 사용한 스키닝 웨이트 페인팅 신경망을 이용하여 삼각형 메시 캐릭터의 스키닝 웨이트를 예측한 결과는 Figure 2 와 같다. 삼각형 메시를 이용하여 구한 SDF 그리드와, 스켈레톤, 그리고 삼각형 메시의 각 꼭지점들을 신경망에 입력하여 각 꼭지점의 스키닝 웨이트를 구하였다. 같은 관절에 영향을 받는 꼭지점은 같은 색깔로 칠하였다.
Figure 2는 본 논문의 방법을 점구름(Point Cloud)으로 만든 캐릭터에 적용하고, 다른 자세를 적용한 결과이다. 캐릭터 내부에서 1500개의 점을 샘플링 하여 각 점의 스키닝 웨이트를 구한 후 각 점이 영향을 받는 관절에 따라 다른 색깔을 칠하였다. 이처럼 본 논문의 방법은 SDF로 얻은 모양 정보와 스키닝 웨이트를 구할 지점의 좌표를 이용하기 때문에 삼각형 메시 이외의 표현 방식을 사용한 캐릭터에도 적용할 수 있다.
Table 3은 스키닝 웨이트 페인팅 자동화와 관련된 최신 연구와 본 연구의 결과를 정량적으로 평가한 표이다. 정밀도(Precision)과 재현률(Recall)은 삼각형 메시의 특정 정점이 스켈레톤의 관절에 영향을 받는지를 예측한 결과이다. 기존 연구들[7-9]에서와 같이 특정 관절에 해당하는 웨이트의 값이 1×10-4 이상인 경우를 참으로 하여 계산하였다. 평균 L1 노름 (average L1-norm)은 정점의 각 관절에 대한 웨이트 값들을 벡터로하여 원본 데이터와 예측한 데이터 사이의 L1 거리를 의미한다. 본 논문에서는 SDF를 이용하여 삼각형 메시 이외의 캐릭터에도 사용할 수 있는 방법을 제안하였으나 삼각형 메시에 대한 결과는 최신 연구들과 비교하였을 때 떨어지는 것을 알 수 있다.
Table 3:
Quantitative result comparison with the state-of-the-art techniques
|
Method |
Precision(%) |
Recall(%) |
Avg L1 |
|
NeuroSkinning[7] |
82.3 |
79.7 |
0.41 |
|
RigNet[8] |
82.3 |
80.8 |
0.39 |
|
SkinningNet[9] |
87.0 |
80.8 |
0.33 |
|
Ours |
53.0 |
60.5 |
0.93 |
Download Excel Table
5. 결론
기존의 스키닝 웨이트 페인팅 자동화 기술들은 삼차원 애니메이션에서 주로 사용되는 삼각형 메시 캐릭터에 국한되어 있었다. 최근 기술의 발전으로 인해 다양한 표현 방법이 사용되기에 본 논문에서는 SDF를 활용하여 점 구름과 같은 다른 방법으로 표현된 캐릭터에도 스키닝 웨이트 페인팅을 수행할 수 있게 하였다.
그러나 본 연구에는 여러 한계점이 존재한다. 먼저 삼각형 메시 캐릭터의 스키닝 웨이트를 구하는 경우, 삼각형 메시를 직접 입력하는 기존 연구들의 결과가 메시를 SDF로 변환해야 하는 본 논문의 방법보다 더 좋은 결과를 보여준다. 따라서 이 방법을 발전시켜 더욱 정확한 결과를 얻을 수 있도록 추가적인 연구가 필요하다.
또한 SDF 그리드가 가지는 문제인 낮은 해상도로 인하여 복잡한 구조가 SDF 그리드 상에 표현되지 않는 경우가 생길 수 있다. 따라서 더 복잡한 형태의 캐릭터의 경우 Figure 4와 같은 잘못된 결과가 나올 수 있다. 이러한 문제를 해결하기 위하여 더 높은 해상도의 SDF 그리드를 사용할 경우 메모리와 연산 시간의 문제가 생길 수 있다.
Figure 4:
Failure case. If the resolution of the voxel is not sufficient, tow points that are apart can be adjacent on the SDF grid
Download Original Figure
본 논문의 연구 결과를 통해서 암묵적인 삼차원 물체 표현 방식인 SDF로 스키닝 웨이트 페인팅 자동화를 수행할 수 있다는 것을 보여주었다. 추가적인 연구를 통해 더욱 빠른 학습 시간과 정확한 결과를 얻을 수 있도록 할 필요가 있다. 또한 스키닝 웨이트뿐만이 아닌 스켈레톤까지 SDF를 활용하여 구해 전체 리깅 과정을 자동화하는 연구도 수행할 수 있다.
감사의 글
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF-2020R1A2C1012847).
References
T. Magnenat, R. Laperrière, and D. Thalmann, “Joint dependent local deformations for hand animation and object grasping,” Canadian Inf. Process. Soc,” Report, 1988.

L. Kavan, S. Collins, J. ˇZ ´ara, and C. O’Sullivan, “Skinning with dual quaternions,” in Proceedings of the 2007 symposium on Inter-active 3D graphics and games, 2007, Conference Proceedings, pp. 39–46.


I. Baran and J. Popovi´c, “Automatic rigging and animation of 3d characters,” ACM Transactions on graphics (TOG), vol. 26, no. 3, pp. 72–es, 2007.


R. Wareham and J. Lasenby, “Bone glow: An improved method for the assignment of weights for mesh deformation,” in Articulated Motion and Deformable Objects: 5th International Conference, AMDO 2008, Port d’Andratx, Mallorca, Spain, July 9-11, 2008. Proceedings 5. Springer, 2008, Conference Proceedings, pp. 63–71.


A. Jacobson, I. Baran, J. Popovic, and O. Sorkine, “Bounded biharmonic weights for real-time deformation,” ACM Trans. Graph., vol. 30, no. 4, p. 78, 2011.


O. Dionne and M. de Lasa, “Geodesic voxel binding for production character meshes,” in Proceedings of the 12th ACM SIGGRAPH /Eurographics Symposium on Computer Animation, 2013, Con-ference Proceedings, pp. 173–180.


L. Liu, Y. Zheng, D. Tang, Y. Yuan, C. Fan, and K. Zhou, “Neuro-skinning: Automatic skin binding for production characters with deep graph networks,” ACM Transactions on Graphics (TOG), vol. 38, no. 4, pp. 1–12, 2019.


Z. Xu, Y. Zhou, E. Kalogerakis, C. Landreth, and K. Singh, “Rignet: Neural rigging for articulated characters,” arXiv preprint arXiv: 2005.00559, 2020.

A. Mosella-Montoro and J. Ruiz-Hidalgo, “Skinningnet: Two-stream graph convolutional neural network for skinning prediction of synthetic characters,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, Conference Proceedings, pp. 18 593–18 602.


P. Li, K. Aberman, R. Hanocka, L. Liu, O. Sorkine-Hornung, and B. Chen, “Learning skeletal articulations with neural blend shapes,” ACM Transactions on Graphics (TOG), vol. 40, no. 4, pp. 1–15, 2021.


F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfardini, “The graph neural network model,” IEEE transactions on neural networks, vol. 20, no. 1, pp. 61–80, 2008.



J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun, “Spectral net-works and locally connected networks on graphs,” arXiv preprint arXiv:1312.6203, 2013.

M. Defferrard, X. Bresson, and P. Vandergheynst, “Convolutional neural networks on graphs with fast localized spectral filtering,” Advances in neural information processing systems, vol. 29, 2016.

D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik, and R. P. Adams, “Convolutional net-works on graphs for learning molecular fingerprints,” Advances in neural information processing systems, vol. 28, 2015.

T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” arXiv preprint arXiv:1609.02907, 2016.

F. Monti, D. Boscaini, J. Masci, E. Rodola, J. Svoboda, and M. M. Bronstein, “Geometric deep learning on graphs and manifolds using mixture model cnns,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, Conference Proceedings, pp. 5115–5124.


J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural message passing for quantum chemistry,” in International conference on machine learning. PMLR, 2017, Conference Pro-ceedings, pp. 1263–1272.

Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M. Solomon, “Dynamic graph cnn for learning on point clouds,” Acm Transactions On Graphics (tog), vol. 38, no. 5, pp. 1–12, 2019.


A. Zeng, S. Song, M. Nießner, M. Fisher, J. Xiao, and T. Funkhouser, “3dmatch: Learning local geometric descriptors from rgb-d reconstructions,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, Conference Pro-ceedings, pp. 1802–1811.



A. Dai, C. Ruizhongtai Qi, and M. Nießner, “Shape completion using 3d-encoder-predictor cnns and shape synthesis,” in Pro-ceedings of the IEEE conference on computer vision and pattern recognition, 2017, Conference Proceedings, pp. 5868–5877.

D. Stutz and A. Geiger, “Learning 3d shape completion from laser scan data with weak supervision,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, Conference Proceedings, pp. 1955–1964.


A. Bozic, P. Palafox, M. Zollhofer, J. Thies, A. Dai, and M. Nießner, “Neural deformation graphs for globallyconsistent non-rigid reconstruction,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, Conference Proceedings, pp. 1450–1459.


B. Mildenhall, P. P. Srinivasan, M. Tancik, J. T. Barron, R. Ramamoorthi, and R. Ng, “Nerf: Representing scenes as neural radiance fields for view synthesis,” Communications of the ACM, vol. 65, no. 1, pp. 99–106, 2021.


A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, and L. Antiga, “Pytorch: An imperative style, high-performance deep learning library,” Advan-ces in neural information processing systems, vol. 32, 2019.

M. Fey and J. E. Lenssen, “Fast graph representation learning with pytorch geometric,” arXiv preprint arXiv:1903.02428, 2019.

D. P. Kingma and J. Ba, “Adamml: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014.

<저 자 소 개>
설 효 석

권 태 수

-
1996-2000 서울대학교 전기컴퓨터공학부 학사
-
2000-2002 서울대학교 전기컴퓨터공학부 석사
-
2002-2007 한국과학기술원 전산학전공 박사