1 서론
3D디지털 컨텐츠의 수요가 증가함에 따라, 3D 메쉬 상에 의미 있는 정보를 직접 삽입하는 기술이 지속적으로 연구되고 있다 [1-3]. 특히 제품 마킹, 디지털 워터 마킹, 모델 식별 등 다양한 분야에서 3D 객체의 표면에 텍스트 형태의 정보를 표현하는 기술은 중요한 역할을 한다 [4-7]. 이러한 기술을 구현하기 위해서, 객체의 곡면 형상을 고려한 자연스러운 텍스트 삽입 기법이 요구된다. 그러나 기존의 3D 텍스트 삽입 방식 [4,5,6,8]은 삽입 영역이 평평한 경우에만 안정적으로 적용되며, 곡률이 큰 메쉬의 표면에서는 Figure 1(a)와 같이 텍스트의 형상 왜곡이 발생하여 시각적 부조화가 발생할 수 있다는 한계가 존재한다.

본 연구는 이러한 한계를 극복하기 위해, 3D 삼각형 메쉬 형상에 기반한 텍스트 메쉬 생성 기법을 제안한다. 제안된 방법은 TrueType 폰트 [9]의 윤곽선 제어점(control points)을 사용자가 정의한 메쉬 위의 자유 형상 곡선 [10]에 따라 메쉬 표면 위로 맵핑하고, 메쉬의 곡률을 반영한 측지 베지에 곡선(geodesic Bézier curve) [11]을 이용하여 텍스트의 윤곽선을 자연스럽게 재구성한다. 이를 통해 곡률이 큰 표면에서도 텍스트를 형상 왜곡 없이 삽입할 수 있다(Figure 1(b)). 더 나아가, 본 연구에서는 정적 맵핑과 동적 맵핑의 두가지 방식을 통해 사용자의 요구에 따른 텍스트의 다양한 표현을 가능하게 하며, 이를 기반으로 메쉬 표면에 텍스트를 양각 및 음각 형태로 삽입하거나 독립적인 메쉬를 생성하는 다양한 응용 가능성을 제시한다.
2. 관련 연구
본 연구는 문자의 윤곽선 제어점을 3D 삼각형 메쉬에 맵핑하여, 곡률을 반영한 텍스트 메쉬를 생성하는 방법을 제안한다. 본 절에서는 기존의 텍스트 삽입 방식과 맵핑을 위한 메쉬 위 곡선 생성 기법을 검토하고, 본 연구와의 차별성을 다룬다.
Cao 등 [4]은 메쉬의 평평한 영역을 2차원 평면으로 맵핑하고, 해당 평면에 2차원 이진 형태의 폰트 정보를 할당하여 텍스트를 삽입하는 기법을 제시하였다. Yan 등 [5]은 비트 맵 기반의 폰트 정보를 메쉬의 평평한 영역에 맵핑하여 메쉬 위에 텍스트를 삽입하는 기법은 제시하였다. 두 접근법은 2차원 폰트 데이터를 기반으로 메쉬 위에 텍스트를 삽입한다는 공통점을 가진다. 하지만 이는 평평한 영역에 한정되어 적용 가능하며, 이를 위해 메쉬를 세분화하는 전처리 과정이 요구되는 한계가 존재한다. Dhiman등 [8]은 실시간 증강 현실 환경에서 다국어 텍스트를 생성하기 위해, 2차원 곡선으로 구성된 윤곽선을 기반으로 3D 텍스트 메쉬 생성 기법을 제시하였다. Li 등[6]은 트루타입 폰트(TrueType Font, TTF)의 윤곽선을 샘플링하고 제약된 들로네이 삼각화
(constrained Delaunay triangulation)를 통해 3D 텍스트 메쉬 생성 방법을 제시하였다. 또한, 생성된 텍스트 메쉬를 대상 3D 메쉬와 Boolean 연산을 통해 삽입하는 방법을 제시하였다. 그러나 Boolean 연산 기반의 접근은 삽입 대상이 되는 메쉬 표면이 평평할 경우에만 안정적으로 동작하며, 복잡하거나 곡률이 큰 영역에서는 적용이 어렵다는 한계가 존재한다. Singh 등[7]은 텍스트 기반의 워터마크(watermark)를 3D 메쉬 표면에 삽입하는 기법을 제안하였으며, 최적의 삽입 위치를 학습을 통해 결정하였다. 하지만 이 방법은 계산 비용이 크고 처리 시간이 길다는 단점이 있으며, 학습에 사용된 데이터가 주로 단순한 메쉬로 구성되어 있어 복잡한 모델에 대한 예측 정확도가 낮다는 한계가 존재한다. 위의 기존 연구들은 텍스트 삽입 영역이 평평한 표면으로 제한된다는 공통적인 한계를 가지며, 곡률이 높은 메쉬 표면에서는 자연스러운 텍스트 삽입이 어렵다. 본 연구는 측지 곡선(geodesic curve)을 기반으로 텍스트의 윤곽선을 메쉬의 형상에 따라 재구성함으로써, 곡률이 높은 표면에서도 자연스러운 텍스트 삽입을 가능하게 한다.
유클리드 거리(Euclidean distance)는 두 점을 잇는 선분의 길이로 정의되는 반면, 측지 거리(geodesic distance)는 3D메쉬 표면을 따라 이동할 수 있는 최단 경로로 정의된다. 이러한 측지 거리를 효율적이고 정확하게 계산하는 방법에 대한 연구는 오랜 기간 동안 활발히 이루어져 왔다[12-17].
Mitchell 등[12]이 제안한 MMP 알고리즘과 Chen 등[13]이 제안한 CH 알고리즘은 메쉬 상에서 최단 거리를 계산하는 대표적인 알고리즘으로, 각각 O(n2logn)과 O(n2)의 시간 복잡도를 가진다. Bommes 등[14]은 메쉬의 한 점에서 시작하여 window propagation 방식을 통해 측지 거리를 계산하는 방식을 제안하였으며, Tang 등[15]은 각 삼각형에 대해 2차원 평면 상의 가상의 시작점을 설정 후, 각 정점까지의 거리를 계산하고 전파하는 방식을 제안하였다. Trettner 등[16]은 삼각형 메쉬 위에서 가상 소스 전파 개념을 통해 높은 메모리 효율성과 CPU 및 GPU 병렬 처리가 가능한 알고리즘을 제안하였다. Li 등[17]은 기존 방식들이 가지는 측지 경로의 불연속성과 도함수 계산의 어려움을 해결하기 위해, C2연속성을 만족하는 측지 거리 함수를 제안하였다.
Park 등[1]은 리만 다양체(Riemannian manifolds) 상의 베지에 곡선 개념을 확장하였으며, Morera 등[11]은 이를 삼각 메쉬 상에서 구현 가능한 측지 베지에 곡선 형태로 발전시켰다. 측지 베지에 곡선은 기존의 de Casteljau 알고리즘을 측지 거리 개념에 기반하여, 제어점 간의 곡선을 메쉬 표면을 따라 정의한다. Ha 등[10]은 삼각 메쉬 상에서 연속적이고 부드러운 곡선을 정밀하게 제어하기 위해 측지 허밋 스플라인 곡선(geodesic Hermite spline curve)으로 확장하였다. 이를 통해 사용자는 메쉬 위의 점들을 정확히 통과하는 자유 형상의 곡선을 생성할 수 있다. 한편, Polthier 등[18]은 기존의 최단 경로 기반 측지 거리와는 다른 방식의 직선 측지 거리(straightest geodesic distance)를 제안하였다. 직선 측지 거리는 메쉬 위의 한 점과 주어진 방향 벡터를 기반으로 계산되며, 경로가 삼각형의 에지만 지날 경우 기존의 측지선과 동일하지만, 정점을 통과할 경우에는 곡률을 최소화하는 방향으로 경로가 계산된다.
본 연구에서는 이러한 직선 측지 거리 개념을 활용하여 폰트 윤곽선의 제어점을 메쉬 상에 맵핑한 뒤, 측지 베지에 곡선을 이용해 윤곽선을 근사하는 폴리라인(polyline)을 구성함으로써 메쉬 형상을 반영한 텍스트 메쉬를 효과적으로 생성하고자 한다.
3. 메쉬 형상 기반 3D 텍스트 메쉬 생성
트루타입 폰트(TrueType Font, TTF) [9]는 벡터 기반의 글꼴 포맷으로, 각 폰트의 윤곽선은 다수의 폐곡선(closed curve) 들로 정의된다. 각 폐곡선은 다음과 같이 정의되는 선분(line segment) L(t)와 2차 베지에 곡선(quadratic Bézier curve) C(t)의 집합으로 구성되며, 이는 폰트의 윤곽선 형상을 정교하게 표현하는 데 사용된다(Figure 2(a)):
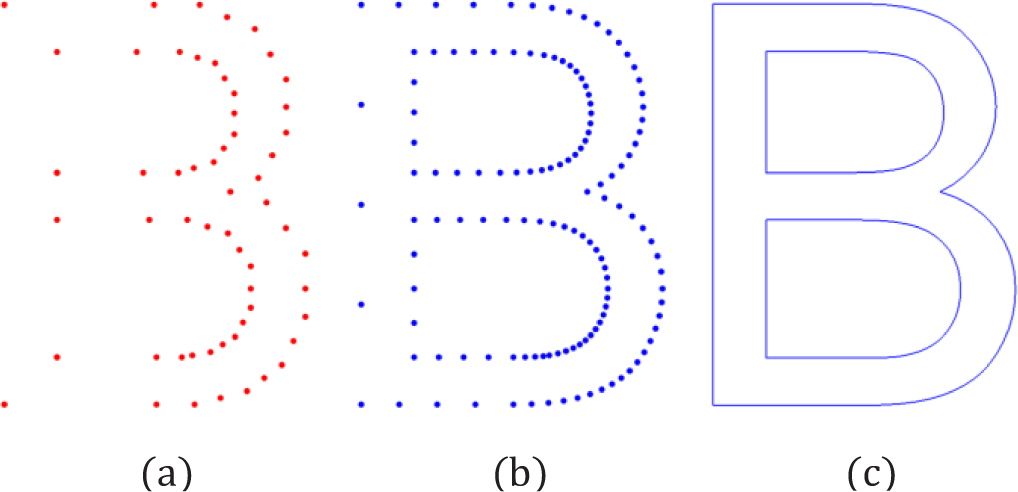
여기서, t∊[0,1]이고 pi ∊ ℝ2는 직선 또는 곡선의 제어점을 나타낸다. 이와 같이 곡선을 이용한 문자의 윤곽선 표현 방식은 해상도나 크기에 관계없이 부드러운 곡선과 날카로운 모서리를 동시에 정확하게 표현할 수 있다. 본 연구에서는 트루타입 폰트로부터 문자의 윤곽선을 구성하는 각 직선 및 곡선 구간의 제어점 정보를 추출한 후, de Casteljau 알고리즘을 이용하여 각 선분 L(t)와 곡선 C(t)를 일정한 간격으로 샘플링하고(Figure 2(b)), 이를 통해 얻어진 점들을 선분으로 연결함으로써, 문자의 윤곽선을 근사하는 닫힌 폴리 라인(closed polyline)을 구성할 수 있다(Figure 2(c)).
본 논문에서는 메쉬 M위에서 사용자가 정의한 3차원 자유 형상 곡선 D(t)을 이용하여 텍스트 메쉬가 위치할 영역 및 형상을 정의한다. 각 문자의 윤곽선을 정의하는 제어점 {pi}는 사용자 지정한 곡선 D(t) 위의 맵핑 구간 [ts,te]⊂[0,1] 상에 정렬되며, 윤곽선의 가로 길이가 1이 되도록 정규화 한다.
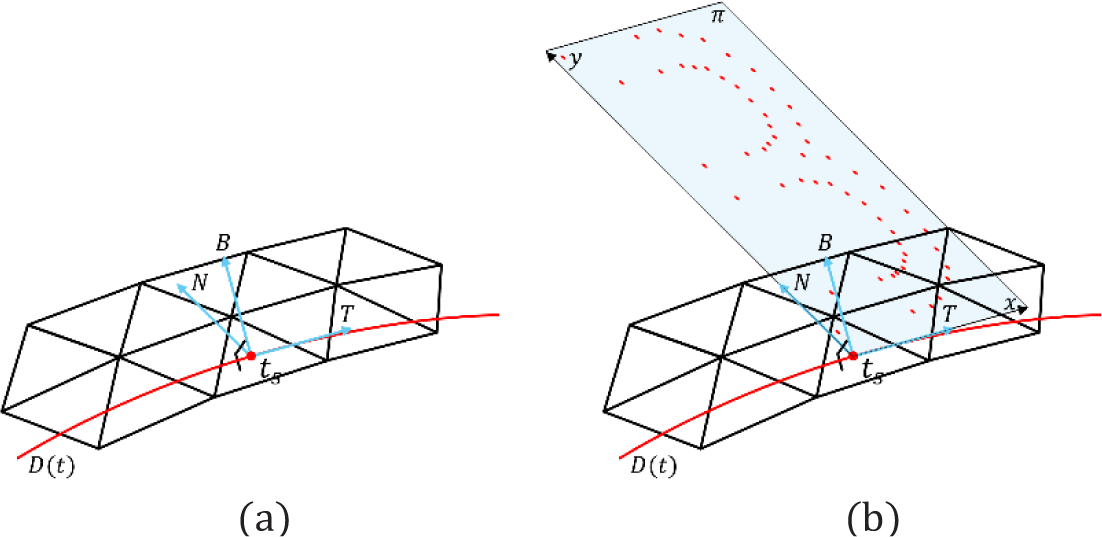
시작 파라미터 ts에 대해 곡선의 프레네 틀장(Frenet frame) {T(ts),N(ts),B(ts)}을 계산하고, 이를 기반으로 다음과 같이 텍스트 메쉬가 위치할 로컬 좌표계 {T(ts),N(ts),B(ts)}를 정의한다(Figure 3):
-
· T(ts): 곡선 위의 점 D(ts)에서의 접선 벡터(x축)
-
· N(ts): 접선 벡터 T(ts)를 점 D(ts)가 놓인 삼각형의 법선 벡터를 축으로 하여 90° 회전시킨 벡터 (y축)
-
· B(ts): 종 법선 벡터 B(ts)=T(ts)×N(ts)(z축)
-
· 원점(origin): 시작 점 D(ts)
두 벡터 T(ts),N(ts)와 시작 점 D(ts)는 모두 동일한 삼각형 위에 존재하므로, 벡터 B(ts)는 해당 삼각형의 법선 벡터로 간단히 계산할 수 있다. 이때 로컬 좌표계 상의 제어점들은 모두 아래와 같이 정의되는 평면 π 상에 존재하게 되며, π는 ts에서 곡선이 속한 삼각형의 평면과 일치한다(Figure 3(b)).
또한, 곡선 구간의 양 끝점 D(ts),D(te)간의 측지 거리 λ를 이용하여 텍스트 메쉬의 스케일 팩터를 정의한다. 이는 제어점을 통해 생성될 텍스트 메쉬의 크기 조절을 가능하게 한다. 본 연구에서는 제어점 pi=(xi,yi,0)의 변형된 위치 p̃i=(x̃i,ỹi,0)를 메쉬 M위로 맵핑하기 위해 다음과 같이 두 가지 맵핑 방식을 제안한다.
첫 번째, 정적 맵핑(static mapping) 방식은 D(ts)에서 정의된 로컬 좌표계 {T(ts),N(ts),B(ts)}를 기준으로 변형된 제어점 p̃i를 직선 측지 벡터(Algorithm 1) [18]로 변환하여 메쉬 표면 위로 맵핑하는 방식이다(Figure 4). 이때, 변형된 제어점 p̃i는 다음과 같이 계산된다.
Require: Start point S, direction vector V, Target mesh M
T ← set triangle containing point S
P← set point current point S
D ← set direction V
L ← 0; total length
forL ≤ |V| do
Compute intersection of ray (P, D) with T
if intersection hits an edge ethen
T ← adjaccnt triangle across e
P ← intersection point
D ← rotate D to preserve angle adjacent triangle
L ← add distance from previous P to new P
else if no intersection then
P ← calculate end points in T
end if
end for
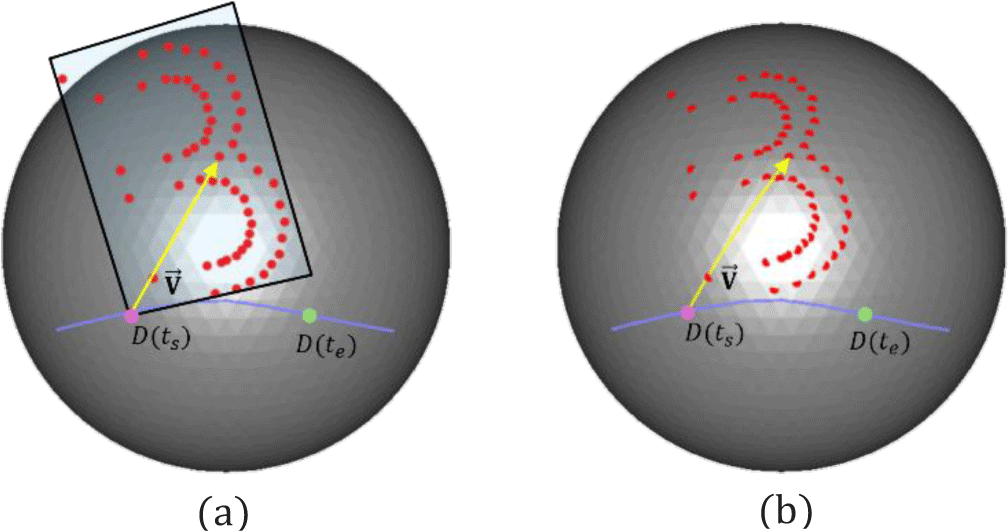
Algorithm 1은 직선 측지선을 계산하는 기법으로, 측지선의 교차점과 삼각형 T의 교차점이 에지 위에 위치할 경우, 방향 벡터 D는 인접한 삼각형으로 연속적으로 연장된다. 교차점이 정점에 위치하는 경우, 벡터 D는 해당 정점에서 형성되는 각도들을 고려하여 양측 내각을 이등분하는 방향으로 전파된다. 이를 이용하여 각 제어점 p̃i를 메쉬 표면 위로 맵핑 할 수 있다.
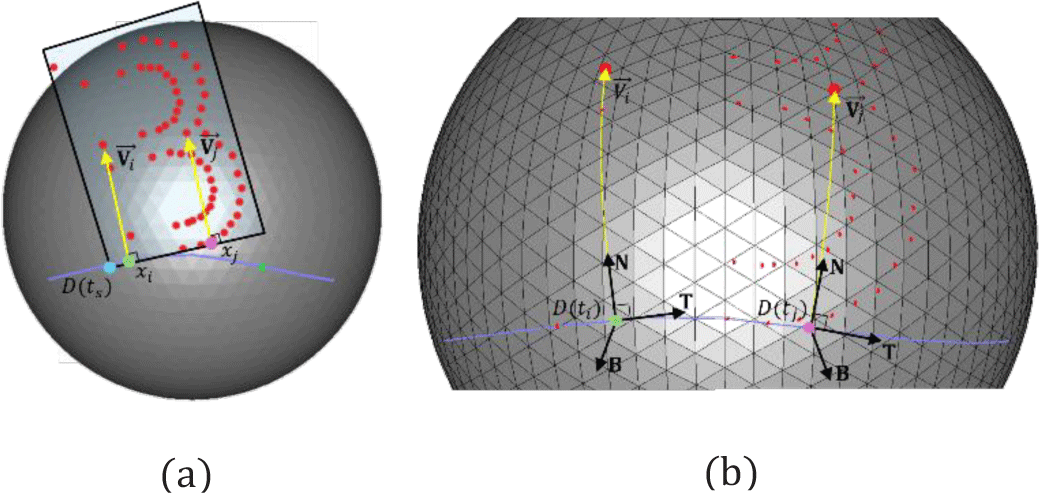
두 번째, 동적 맵핑 방식(dynamic mapping method)은 우선, 제어점 pi의 x좌표를 이용하여 맵핑 파라미터 tp를 다음과 같이 계산한다:
이후, 원점 D(tp)에서의 로컬 좌표계 {T(tp),N(tp),B(tp)}를 기준으로 변형된 제어점 p̃i을 직선 측지 벡터로 변환하여 맵핑한다. 이때 변형된 제어점 p̃i은 다음과 같이 계산된다:
동적 맵핑 방식은 곡선 D(t)의 형태에 따라 더 유연하게 문자의 형상을 곡면에 맵핑 시킬 수 있다는 장점이 있으나, 제어점을 통해 생성되는 윤곽선이 자기 교차(self-intersection)를 일으킬 수 있다는 문제가 있다.
폰트의 윤곽선은 다수의 베지에 곡선으로 표현되며, 각 곡선을 일정 간격으로 샘플링 하여 닫힌 폴리라인(closed polyline)으로 근사할 수 있다(Figure 6(a)). 본 연구에서는 메쉬 표면 위에 자연스럽게 위치한 윤곽선을 얻기 위해 일반적인 유클리드 공간에서의 선형 보간이 아닌 다음과 같은 두 지점을 연결하는 측지선을 보간하는 geodesic de Casteljau 알고리즘 (algorithm 2)을 사용하며[11], 최종적으로 각 측지 베지에 곡선을 일정 간격으로 샘플링하여 메쉬 표면 위에 정의된 닫힌 윤곽선 폴리라인을 구성한다(Figure 6(a)). 여기서, glerp(·)는 두 점 사이의 측지 거리를 따라 보간하는 연산이다.
Require: Control point (P0,P1,…,Pn), parameter t ∈ [0,1]
C(t) ← point on curve
fori = 1, …, ndo
forj = 0, … n-ido
Pi ← glerp(Pj,Pj+1,t)
end for
end for
C(t) ← P0
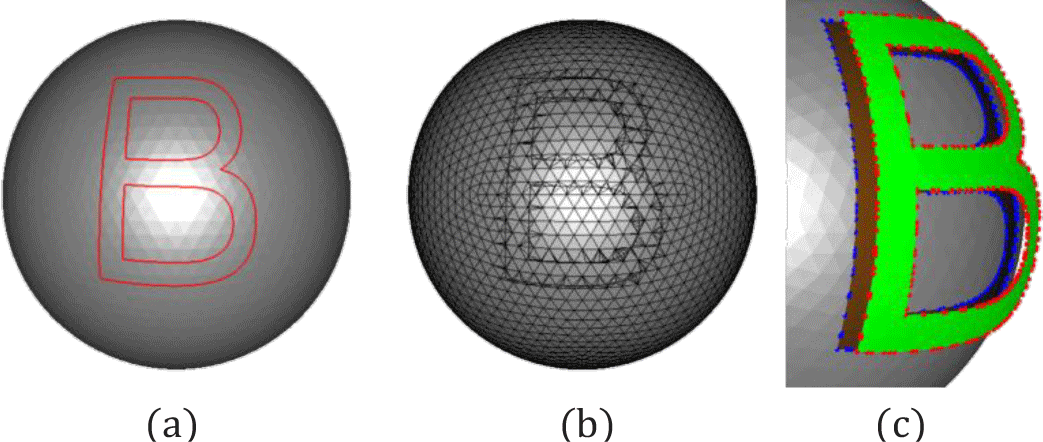
생성된 윤곽선 폴리 라인을 기준으로, 메쉬 M의 삼각형들을 절단하여 [19](Figure 6(b)) 텍스트 메쉬 생성을 위한 영역을 분리한다. 이 과정에서 다음의 두 가지 정보를 얻을 수 있다(Figure 6(c)).
· TF: 폴리 라인으로 둘러싸인 내부 삼각형 집합.
· Vpair: 절단 시 생성된 경계 정점 쌍 집합 .
이후, 텍스트 메쉬의 생성 목적에 따라 다음의 두 가지 방식 중 하나로 텍스트 메쉬를 생성한다. 텍스트 메쉬를 독립적인 객체로 생성할 경우, 절단된 삼각형 집합 TF을 앞면으로 정의하고, 각 삼각형의 법선 벡터를 반전시켜 복사함으로써 뒷면 삼각형 집합 TB를 생성한다. 이어서, TF의 모든 정점에 대해 평균 법선 벡터 n̅방향으로 사용자가 정의한 거리 d만큼 평행이동 시킨다.
여기서 |TF|는 집합 TF에 속한 삼각형의 수이고, nT는 삼각형 T의 법선 벡터이다. 마지막으로, 앞면과 뒷면에 대응하는 경계 정점 쌍을 연결하여 측면을 구성함으로써 3차원 텍스트 메쉬를 생성한다(Figures 7(e) and 7(f)).
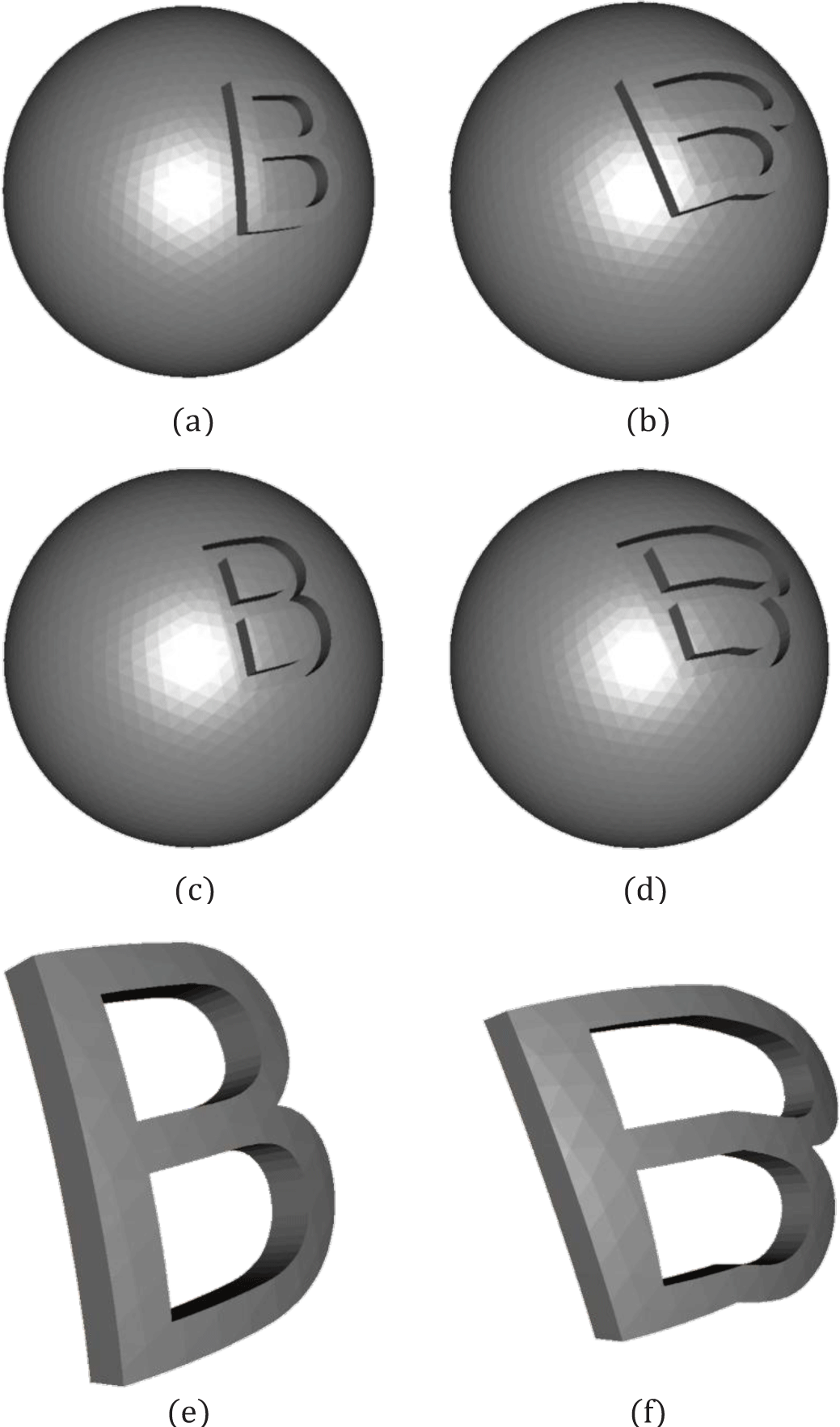
텍스트 메쉬를 기존 메쉬 M의 표면에 양각(engrave) 혹은 음각(emboss)의 형태로 삽입하고자 할 경우, 앞면 삼각형 집합 TF를 평균 법선 벡터 n̅ 방향으로 평행이동 시킨다. 양각의 경우 +d, 음각인 경우 -d 방향으로 이동되며, 측면은 절단 과정에서 생성된 정점 쌍 Vpair을 연결하여 생성한다. 이를 통해 메쉬에 자연스럽게 삽입된 텍스트 형상을 구현할 수 있다(Figure 7).
4. 실험 결과
본 연구에서 제안하는 방식은 C++ 환경에서 구현되었으며, 트루 타입 폰트의 윤곽선 정보를 추출하기 위해 Free Type 라이브러리[20]를 사용하였다. 실험은 Intel Core i9-14900K CPU, 64GB RAM, NVIDIA RTX 4060 Ti를 사용하는 Window 11 기반 데스크톱 환경에서 수행되었다. 윤곽선의 제어점을 메쉬의 표면 위로 맵핑하는 과정에서 사용되는 정적 맵핑과 동적 맵핑은 CPU 기반 병렬처리를 적용하였다. Table 1은 텍스트 메쉬의 기반이 되는 3D 메쉬들의 주요 특성을 요약하며, Table 2는 Arial 폰트를 기준으로 생성할 문자에 대한 폰트 정보를 나타낸다.
| Models | Box | Bunny | Armadillo |
|---|---|---|---|
| # of vertices | 1538 | 8327 | 172974 |
| # of triangles | 3026 | 16650 | 345955 |
| Feature | Sharp edges | Smooth surface | Complex surface |
| Font | B | L | O |
|---|---|---|---|
| # of control points | 60 | 6 | 42 |
| Feature | Composite curve | Only segment | Only curve |
| Ctrl points creation | 0.7636 | 0.3418 | 0.4984 |
본 연구에서 제안하는 방식은 사용자가 3D 메쉬 표면 위에 자유 형상 곡선을 지정함으로써 텍스트 메쉬가 생성될 영역을 정의하는 것으로 시작된다. 이후, 제안된 두가지 맵핑 방식(3.2)에 따라 텍스트 윤곽선의 제어점을 변형한 뒤, 이를 메쉬 표면 위로 맵핑한다. 맵핑된 제어점을 기반으로 윤곽선에 근사하는 측지 베지에 곡선을 구성하여 텍스트의 윤곽선을 생성하고, 이를 따라 메쉬를 절단한 뒤 절단 면을 이동시켜 텍스트의 전면을 구성한다. 이러한 과정은 제어점이 위치할 표면의 곡률에 제한 없이, 메쉬 형상을 반영하는 텍스트 메쉬를 안정적으로 생성할 수 있게 한다.
Figure 8은 각 동일한 곡선, 위치, 크기를 기준으로 서로 다른 메쉬에서 텍스트 메쉬를 생성한 결과이다. 파란 색 곡선은 사용자가 지정한 자유 형상 곡선이며, 해당 곡선을 기준으로 정적 맵핑 방식은 빨간 텍스트로, 동적 맵핑 방식은 파란 텍스트 메쉬로 표현한다. 또한 하나의 곡선에 단일 문자를 배치하는 것이 아니라, Figure 9와 같이 여러 개의 문자를 연속적으로 배치하여 긴 문자열 형태의 텍스트 메쉬를 구성할 수 있다.
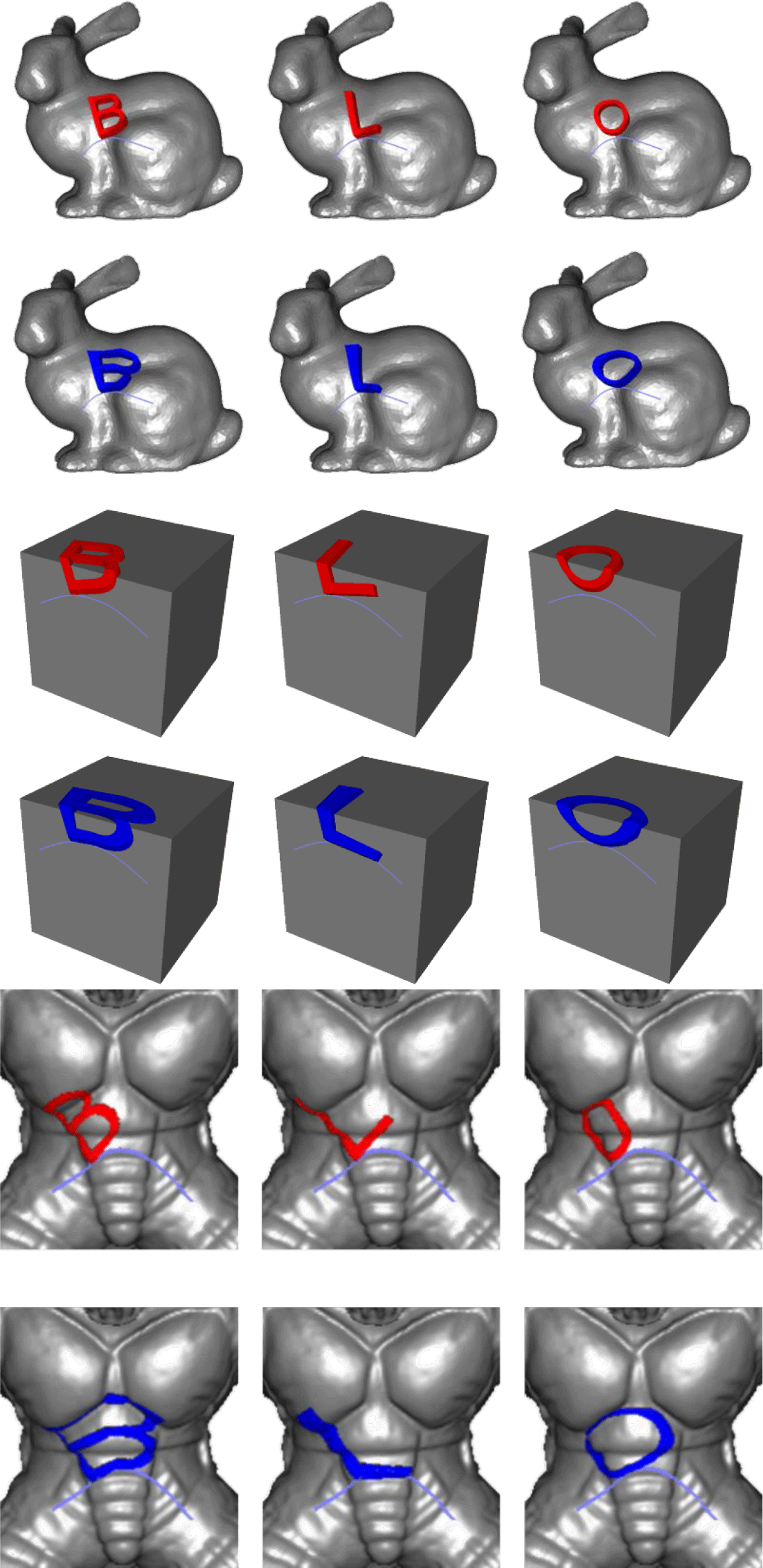
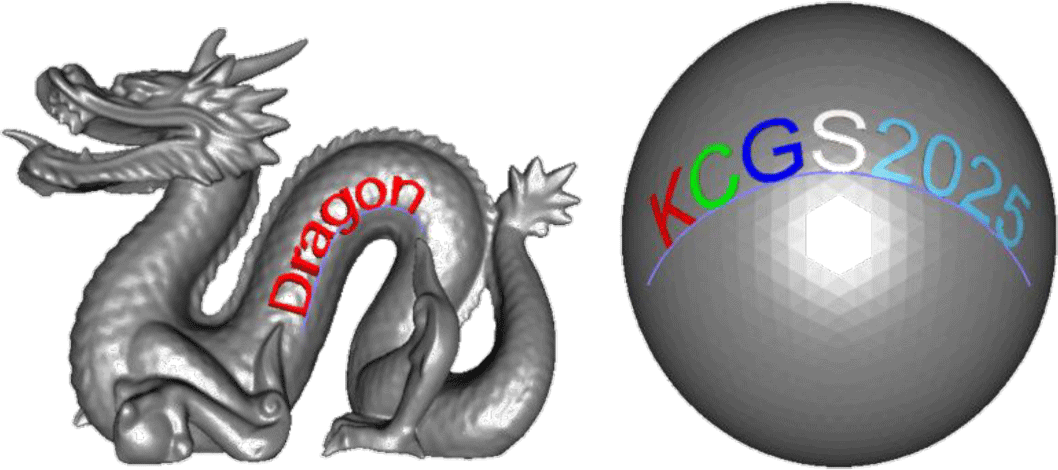
Table 3는 Bunny 모델을 기반으로 각 텍스트 메쉬를 생성할 때 소요되는 각 단계별 시간을 나타낸다. 전체 생성 과정은 제어점 맵핑, 측지 곡선 생성, 텍스트 메쉬 생성으로 구분되며, 최종 경과 시간은 이들을 합산하여 계산된다. 실험에서는 텍스트가 위치할 곡선, 각 텍스트의 크기 및 위치는 모두 동일하다.
| Text | B | L | O | |||
|---|---|---|---|---|---|---|
| Mapping | Static | Dynamic | Static | Dynamic | Static | Dynamic |
| Mapping | 3 | 6 | 3 | 4 | 2 | 4 |
| Curve creating | 2 | 3 | 1 | 1 | 1 | 2 |
| Text mesh | 19 | 20 | 15 | 15 | 17 | 17 |
| total | 24 | 29 | 19 | 20 | 20 | 23 |
동일한 문자를 기준으로 비교하였을 때, 동적 맵핑 방식이 정적 맵핑 방식에 비해 더 많은 시간이 소요된다. 이는 동적 맵핑 과정에서 각 제어점에 대해 프레네 프레임을 계산하기 때문이다. 이외에 측지 베지에 곡선 생성 및 텍스트 메쉬 생성하는 시간은 두 방식 간 큰 시간 차이를 보이지 않는다. 동일한 맵핑 방식을 기준으로 비교하였을 때, 문자 윤곽선 제어점의 수가 적을수록 제어점 맵핑 시간 또한 감소한다. 하지만 “L”과 같이 제어점의 수가 지나치게 적은 경우, 병렬처리 과정에서 발생하는 오버헤드로 인해 오히려 더 시간이 더 소요될 수 있다.
Table 4는 Table 1에 제시된 각 모델을 기반으로 동일한 문자 “B”를 생성할 때의 각 단계 별로 소요되는 시간을 나타낸다. 메쉬의 특징과 상관없이, 모든 단계에서 동적 맵핑 방식이 정적 맵핑 방식보다 더 많은 시간을 소요한다. Box나 Bunny 와 같이 단순한 모델에서는 그 차이가 작으나, Armadillo와 같이 복잡한 형상의 메쉬에서는 그 차이가 크게 증가하는 것을 확인할 수 있다.
| Model | Box | Bunny | Armadillo | |||
|---|---|---|---|---|---|---|
| Mapping | Static | Dynamic | Static Dynamic | Static | Dynamic | |
| Mapping | 2 | 3 | 3 4 | 124 | 179 | |
| Curve creating | 2 | 2 | 1 1 | 71 | 88 | |
| Text mesh | 7 | 7 | 15 15 | 532 | 567 | |
| total | 11 | 12 | 19 20 | 727 | 834 | |
본 연구에서 제안한 텍스트 메쉬 생성 기법은 디지털 보안 및 저작권 보호 분야에서 다양한 방식으로 응용 가능하다. 특히 디지털 3D 워터마크(Digital 3D Watermarking) [2]에 효과적으로 활용될 수 있다. 먼저, 사용자가 자신의 3D 모델의 표면 위에 원하는 텍스트 메쉬를 직접 시각적으로 삽입함으로 써 직관적으로 확인 가능한 시각적 워터마크(visible watermarking)를 구현할 수 있다(Figure 10(a)). 이를 통해 모델 저작권을 명확히 표기할 수 있으며 시각적 디자인 요소로도 활용 가능하다. 또한, 텍스트의 윤곽선을 근사하는 측지 베지에 곡선을 이용하여 메쉬 표면을 세분화하여 외형상 변화는 발생시키지 않는 비시각적 워터마크(invisible watermarking)을 삽입할 수 있다(Figure 10(b)). 이러한 방식은 시각적인 변화는 없으나, 메쉬의 형상은 보존하면서 모델에 대한 저작권을 명시할 수 있다.

더 나아가, 본 연구에서 생성한 3D 텍스트 메쉬는 CAPTCHA와 같은 인간-봇(Bot) 인증 시스템에도 응용 가능하다 [21]. 기존 CAPCHA는 주로 2D 텍스트 기반이나, 3D 텍스트로 확장할 경우 사람은 직관적으로 인식이 가능하지만 자동화된 봇은 그 인식을 어렵게 할 수 있다. 특히, 곡면 위의 텍스트, 비정형 표면의 노이즈, 그리고 시점의 복잡성 등은 인공지능 기반 자동 판독 시스템에 추가적인 어려움을 줄 수 있다.
5. 결론
본 연구에서는 3D 메쉬의 형상을 기반으로 텍스트 메쉬를 생성하거나 삽입하는 기법을 제안하였다. 제안된 방법은 트루타입 폰트로부터 추출한 윤곽선의 제어점을 사용자가 정의한 메쉬 위의 자유 곡선을 따라 맵핑하고, 이를 통해 텍스트 형상을 생성하는 과정을 정적 및 동적 맵핑의 두 가지 방법으로 구현하였다. 단순한 선형 보간이 아닌, 측지 보간 기반의 베지에 곡선을 통해 메쉬 형상을 반영하는 텍스트 윤곽선을 형성하며, 이를 통해 곡률이 높은 비정형 표면에서도 시각적으로 안정적인 텍스트 메쉬를 구현할 수 있음을 실험을 통해 입증하였다. 성능 평가 결과, 동적 맵핑 방식은 정적 방식 대비 계산량이 다소 증가하지만, 텍스트의 곡률에 대한 적응 및 시각적 다양성 측면에서는 더 우수한 결과를 보이며, 양각, 음각, 독립형 텍스트 메쉬와 같이 다양한 표현 방식을 지원하였다. 또한 기존 Boolean 연산 기반 텍스트 삽입 방식과 비교하였을 때, 본 연구 방식은 텍스트의 형상 왜곡 없이 안정적으로 삽입이 가능하다는 장점이 있다. 이러한 특성은 디지털 3D 워터 마킹이나 CAPTCHA와 같은 보안 분야에도 응용될 수 있으며, 특히 시각적 워터마크와 비시각적 워터마크 모두에 적용 가능하다는 점에서 실용성이 높을 것으로 예상된다.
다만, 윤곽선의 각 제어점을 메쉬 위로 맵핑하는 과정에서, 곡률이 극단적으로 높은 영역에서는 직선 측지 거리의 오차로 인해 윤곽선의 자기 교차 현상이 발생할 수 있다. 또한 대부분의 트루 타입 폰트의 외각 윤곽선은 시계 방향, 내곽 윤곽선은 반 시계 방향으로 정의되지만, 일부 폰트는 이를 따르지 않아 본 방법의 적용에 제약이 있을 수 있다. 따라서, 이에 대한 보완을 위한 후속 연구가 요구된다.




