1 서론
컴퓨터 비전, 렌더링, AR/VR 등에서 카메라의 기본 수학적 모 델로 핀홀 카메라 모델(pinhole camera model)이 널리 사용된다. 예를 들어, 카메라 캘리브레이션(camera calibration)에서는 실제 카메라의 내부 파라미터(초점거리, 주점 등)를 추정할 때 핀홀 카 메라 모델을 기반으로 하며, 레이 트레이싱(ray tracing)에서는 카 메라에서 나오는 광선(ray)을 장면에 투사할 때 핀홀 모델을 기반 으로 각 픽셀에서 광선을 생성한다. 핀홀 카메라 모델은 이상적인 카메라로, 완벽한 원근 투영을 수행하여 블러를 발생시키지 않는 다는 특성이 있으며 보편적으로 사용된다.
하지만 핀홀 카메라 모델은 실제 카메라의 복잡한 물리적 특성 을 무시하기 때문에 이미지 왜곡과 비현실적 표현을 초래한다는 문제가 있다. 실제 카메라는 광학적 한계로 인해 렌즈 왜곡(lens distortion)과 디포커스(defocus), 그리고 다양한 광학 수차(optical aberration)에 의한 블러(blur) 현상이 발생한다. 예를 들어, 렌즈 왜곡은 직선을 곡선으로 보이게 하며 특히 광각 렌즈에서 두드 러지게 나타난다. 디포커스로 이미지가 흐릿해지거나 구면수차, 코마수차 등으로 비대칭적인 흐림이 생길 수 있으며 파장에 따라 굴절률이 달라져 색수차가 발생하기도 한다.
실제 카메라를 보다 사실적으로 모사하기 위해 타겟 카메라의 특성을 분석 및 측정하여 시뮬레이션하거나 후처리를 통해 보정 하는 기법들이 개발되어 왔다. 렌즈 왜곡 관련 연구는 초기 이론 적 모델[1, 2, 3]에서 딥러닝 기반 방법[4]까지 오래전부터 발전해 왔으며 OpenCV[5] 등 여러 라이브러리에서 기본적으로 제공한 다. 디포커스는 주로 얇은 렌즈 모델(thin lens model)로 모델링된 다[6, 7]. 광학 수차는 캘리브레이션 이미지와 디컨볼루션(deconvolution) 기법을 통해 이미지 형태의 블러 커널[8]이나 제르니케 다항식(Zernike polynomial)과 같은 저차원 표현[9, 10, 11, 12]으 로 표현된 점확산함수(point spread function, PSF)를 구하는 것이 보편적이다. 최근에는 디포커스와 기타 광학 수차의 블러를 통합 적으로 다루고자 하는 연구[13, 14]가 활발히 수행되고 있다.
그러나 기존의 방법들은 여전히 한계점을 가지고 있다. 기존 기법들은 왜곡, 블러, 비네팅 등의 현상이 모두 동일한 광학계 내 에서 발생함에도 불구하고 이를 독립적으로 처리한다는 문제가 있다. 예를 들어, 빛이 광학계 내부의 부품에 의해 차단되어 발 생하는 비네팅은 광학계 내부를 통과하는 빛의 경로가 이상적인 렌즈와 차이가 있어 발생하는 왜곡 혹은 렌즈 블러와 직접적인 관련이 있다. 이들을 개별적으로 추정할 경우, 상호 얽혀 있는 광 학적 인과관계를 충분히 활용하지 못해 역문제(inverse problem) 해결의 어려움이 커진다는 문제가 있다.
또한, 기존의 방법들이 구한 블러 커널과 같은 제한적인 정보만 으로는 충분한 품질의 시뮬레이션을 보장하기 어렵다는 문제가 있다. 하나의 예로, 다양한 물체로 구성된 복잡한 씬(scene)의 실 사적 렌더링이 있다. 불연속적인 깊이(depth)를 가진 경계에서는 복잡한 형태의 렌즈 블러가 발생할 수 있는데, 이는 다른 물체에 의해 일부분이 가려질 때(occlusion) 광학계에 입사하는 빛의 영 역이 복잡한 모양을 띠기 때문이다[15, 16]. 이러한 경우, 사전에 캘리브레이션을 통해 구한 블러 커널만으로는 모사하기 어렵다. 실사적인 렌더링을 목적으로 다항식 등으로 광학계를 모델링하 고자 하는 연구도 있었다[17, 18, 19]. 그러나 이들은 렌즈 설계 정보나 특수한 데이터를 필요로 하며 이러한 정보를 획득할 수 없을 시 사용할 수 없다는 명확한 한계가 존재한다.
이러한 문제를 해결하기 위해 본 연구에서는 광학적 영상 열화 (디포커스, 왜곡 등)를 통합적으로 모사할 수 있는 광학계 모델을 제안한다. 본 연구의 모델은 미분 가능한 PSF 렌더러(renderer)를 활용하여 타겟 카메라의 PSF와 일치하도록 최적화되며 기존 기 법들보다 더 적은 측정 데이터로 임의의 파라미터에 대한 왜곡, 블러 등을 모사할 수 있다. 또한, 본 모델은 타겟 카메라의 구체 적인 정보를 직접 활용하지 않기 때문에 앞서 언급한 문제점이 발생하지 않으며 이미지 복원을 위한 딥러닝 네트워크의 학습용 데이터셋 합성 등의 다양한 응용 분야에 적극 활용될 수 있다.
2 관련 연구
여기서는 광학 시스템이 이상적인 영상을 생성하지 못해 발생하 는 광학적 영상 열화(optical image degradation)의 주요 요소인 디 포커스, 왜곡, 광학 수차에 대해 다룬다. 디포커스와 왜곡은 넓은 의미에서 광학 수차에 포함되는 개념이나 편의상 별도로 다뤄지 는 경우가 많다. 이에 디포커스, 왜곡, 그리고 이들을 제외한 광학 수차에 대해 순차적으로 설명하고자 한다.
디포커스 디포커스는 초점면과 피사체 간의 거리 불일치로 인 해 발생하는 흐림 현상이다. 초점이 맞지 않는 점광원은 이미지 평면(image plane)에서 원반 형태의 PSF로 나타나며 초점 오차 와 조리개 크기에 의해 그 모양과 크기가 결정된다. 기존에 자주 사용된 디포커스 블러 표현 방법은 얇은 렌즈 모델을 기반으로 하여 디스크 블러(disk blur) 또는 가우시안 블러(Gaussian blur) 와 같은 단순한 PSF로 표현하는 것이다[20, 6, 7]. 그러나 실제 디 포커스 블러는 조리개의 모양, 광학 수차 등에 복합적인 영향을 받으며, 앞의 방법은 이들을 정밀하게 표현하는 데 한계가 있다. 다른 접근 방식으로 이미지 형태의 블러 커널을 직접 추정하는 것이 있으나[21, 22], 이들은 물체 거리 등 각 파라미터에 대한 커널을 개별로 다루기 때문에 다양한 파라미터에 의한 변화를 표 현하는 데 한계가 있다.
왜곡 카메라 왜곡은 실제 렌즈 시스템에서 발생하는 투영의 비 이상성을 의미하며 이는 이상적인 원근 투영(perspective projection)과의 차이로 나타난다. 전통적인 카메라 왜곡 모델은 카메라 에 의해 투영된 이미지 점과 이상적인 원근 투영 점 사이의 변위 를 다항식(radial, tangential distortion 등)이나 기타 수학적 함수 로 근사하여 표현하며 이와 관련하여 다양한 방법[1, 2]이 제안 되어 왔다. 이러한 방식은 구현이 간단하고 소수의 파라미터로도 효과적인 보정이 가능하다는 장점이 있지만 실제 복합렌즈 시스 템에서 발생하는 복잡한 왜곡을 충분히 표현하기에는 부족하다. 최근 이러한 문제를 해결하기 위해 딥러닝 네트워크를 활용하 여 렌즈의 왜곡뿐만 아니라 비네팅(vignetting)까지 표현하는 방 법[4]이 제안되었지만 디포커스와 광학 수차 등 다양한 현상을 통합적으로 다루지 못한다는 한계가 여전히 존재한다.
광학 수차 광학 수차는 렌즈의 물리적 한계로 인해 초점이 맞더 라도 발생하는 다양한 형태의 흐림 및 왜곡 현상을 의미한다. 대 표적으로 구면수차(spherical aberration), 코마수차(coma), 비점 수차(astigmatism) 등이 있으며 이들은 각자 상이한 형태의 PSF 를 가진다. 광학 수차로 인한 블러는 위치에 따라 그 형태와 세 기가 달라지므로 공간적으로 변화하는 PSF 추정이 필수적이다. 이를 다루기 위한 보편적인 방식은 이미지를 패치 단위로 분할하 여 각 패치마다 하나의 PSF를 추정하는 것인데[8, 23, 24], 이는 패치 경계에서의 불연속성 및 경계 아티팩트 문제를 야기할 수 있다.
다른 접근 방식으로는 가우스 함수(Gaussian function)나 제르 니케 다항식 등의 저차원 표현으로 PSF를 모델링하는 방법들이 있다[9, 10, 11, 12]. 이들은 위치에 따른 연속적인 변화를 표현 할 수 있으나 복잡한 블러에 대한 표현 능력은 떨어진다. 최근 표현력을 높이기 위해 딥러닝 네트워크를 사용하는 연구[13]가 제안되었으나 광학적 특성이나 사전 지식을 활용하지 않기 때문 에 많은 양의 학습 데이터에 의존한다는 한계가 존재한다.
기존 연구에서는 광학계 자체를 수학적으로 모델링하여 실제 렌 즈의 이미징 특성을 정밀하게 재현하고자 하는 다양한 시도가 이루어져 왔다[17, 18, 19]. 실제 복합 렌즈 시뮬레이션을 직접적 용하는 것이 가장 높은 정밀도를 제공하지만 이 방식은 연산량이 매우 크다는 한계가 있기 때문에, 이들 연구의 주요 목적 중 하 나는 복합 렌즈 시스템의 물리적 특성을 정확하게 모사하면서도 계산 효율성을 확보하는 데 있다. 대표적으로 다항식 근사나 신 경망 기반 모델을 활용하여 렌즈의 PSF 또는 광선 추적 결과를 예측하는 방법들이 제안되었다. 하지만 이러한 방법들은 모두 직 접적인 광학적 정보(렌즈 디자인, 광선 추적 데이터 등)가 충분히 주어진 상황을 전제로 하기 때문에 해당 정보가 가용하지 않은 상황에서는 사용할 수 없다는 명확한 한계가 존재한다.
3 방법
광선은 3차원 원점(origin) 벡터와 3차원 방향(direction) 벡터로 표현할 수 있다. 그러나 이를 그대로 사용하기에는 몇 가지 단점 이 있다. 첫 번째는 광선과 해당 표현 사이에 일대일 대응이 성립 하지 않는다는 점이다. 예를 들어, 광선에 해당하는 표현을 방향 벡터와 나란하게 이동시킬 경우(원점 벡터 이동) 광선 자체는 변 하지 않지만 표현은 변한다. 이는 뒤에서 설명할 빛의 가역성을 활용하는 데에 문제가 되며 모델 최적화에도 방해가 된다. 두 번 째는 광선의 원점 벡터와 방향 벡터 간에 크기(scale) 차이가 발 생한다는 점이다. 일반적으로 방향 벡터는 길이 또는 특정 축의 성분이 1이 되도록 정규화하여 표현된다. 이럴 경우, 방향 벡터의 성분은 광학계의 크기와 무관하게 1 이하의 작은 값으로 유지되 며, 적절한 스케일링이 없으면 원점 벡터와 크기 차이가 발생하기 때문에 모델의 최적화를 불안정하고 어렵게 만들 수 있다.
이러한 문제를 해결하기 위해 본 연구에서는 두 개의 참조 평 면(z = z1, z = z2)을 사용한 표현법을 도입하였다. 두 참조 평면 에 대해 광선은 4차원 벡터 (x1, y1, x2, y2)로 정의된다. 이는 첫 번째 평면 상의 (x1, y1, z1)을 원점으로 하며 두 번째 평면 상의 (x2, y2, z2)를 지나는 광선을 의미한다. 본 연구에서 사용한 표현 방식은 광선을 기존의 6차원보다 작은 4차원의 일대일 대응 벡터 로 표현할 수 있으며, 앞서 언급한 벡터 성분 간 크기 차이로 인해 발생하는 문제도 완화할 수 있다.
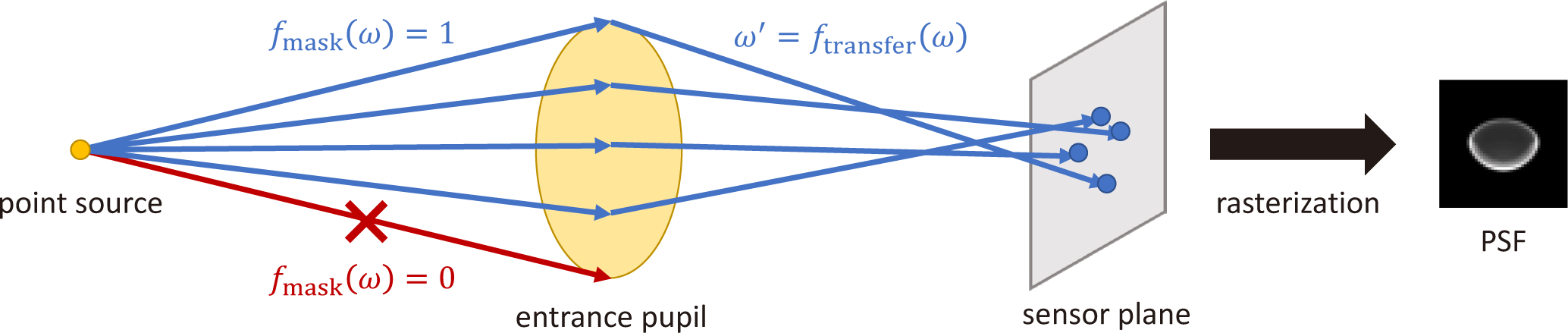
일반적으로 카메라의 렌즈는 여러 싱글렛(singlet) 렌즈를 조합 한 복합렌즈(compound lens)이다. 각 복합렌즈는 다양한 개수, 위치, 곡률, 재료의 싱글렛으로 구성되며 상세한 디자인 정보가 제공되지 않는 한 이를 재구성하는 것은 사실상 불가능하다. 그 러나 렌즈의 디자인이 아니라 기능에만 초점을 둔다면 렌즈를 블랙박스(black-box) 모델로 추상화하여 다룰 수 있다[19]. 기하 광학(geometrical optics)의 관점에서 렌즈는 입사 광선 중 일부를 출사 광선으로 매핑하고 나머지를 차단하는 모델이다. 이때 광 선은 광학계 내부에서 단일 경로로 이동한다고 가정하며 복합렌 즈에서 일어나는 내부 반사(interreflection)와 같은 현상은 무시 한다. 본 연구에서는 광학계를 세 개의 하위 모듈, 입사동공(entrance pupil), 차단 함수(mask function), 그리고 광선 변환 함수 (ray-transfer function)로 구성한다. 여기서 입사동공과 차단 함수 는 입사 광선의 차단 여부를 결정하며 광선 변환 함수는 입사 광 선을 출사 광선으로 매핑한다. 이어서 각각의 구성 요소에 대해 상세히 설명하고자 한다.
입사동공 입사동공은 광학계로 입사하는 광선의 통과 영역을 정의하는 핵심 요소로 z축과 수직한 원형 영역으로 모델링된다. 이 영역은 광선의 진행 방향을 연장했을 때 해당 광선이 통과할 수 있는 공간을 규정하며 수학적으로 다음과 같이 표현된다:
여기서 rp와 z0는 각각 입사동공의 반경과 z축 상의 위치이며 광 선이 Pent 영역과 교차할 경우에만 광학계를 통과할 수 있다. 광선 샘플링은 입사동공 내에서 균일하게 분포된 점을 선택하고 해당 점을 지나는 광선을 생성하는 방식으로 수행된다. 균일 샘플링 방법으로는 입사동공 영역을 균등한 격자로 나누고 각 격자 내 에서 점을 샘플링하는 방식인 층화표집(stratified sampling)[25, 챕터 8]을 사용한다.
차단 함수 차단 함수 fmask : R4 → [0, 1]는 입사 광선의 광도 (radiance) 감쇠율을 결정한다. 이 함수의 목적은 입사동공으로 미처 차단하지 못한 광선을 마스킹(masking)하는 것이다. 이는 특히 축에서 멀리 떨어진(off-axis) 광선이 렌즈의 여러 부품에 의 해 차단되는 비네팅을 표현하는 데에 중요하다. 본 연구에서는 차단 함수를 다층 퍼셉트론(multilayer perceptron, MLP)으로 모 델링하였으며 출력값을 [0, 1] 범위로 정규화하기 위해 마지막 층 에 시그모이드(sigmoid) 활성화 함수를 추가하였다. 또한, MLP 는 저주파수 편향(low-frequency bias)이 있어 매끄러운 함수는 잘 학습하지만 급격한 변화를 표현하기는 어려운 경향이 있기 때 문에 위치 인코딩(positional encoding)[26]을 적용해주었다. 이는 입력 좌표를 고차원 주파수 공간으로 매핑하여 네트워크로 하여 금 다양한 스케일의 기하학적 디테일을 학습할 수 있도록 한다. 본 연구의 실험에서는 4를 인코딩 차수로 선택하여 4종류의 주파 수를 사용하였다.
광선 변환 함수 광선 변환 함수는 차단되지 않은 광선을 출사 광선으로 매핑하는 함수이다. 이때 렌즈의 물리적 특성으로부터 유도된 두 가지 사전 지식을 활용한다. 첫째, 기하광학에서 빛의 경로 가역성에 기반하여 광선 변환 함수 ftrans : R4 → R4는 가역 함수(invertible function)여야 한다. 둘째, 렌즈 굴절에 의한 경로 변화가 급격하지 않고 점진적으로 발생한다는 특성상 이 함수 는 Lipschitz 연속성을 만족해야 한다. 이러한 조건을 충족하기 위해 본 연구에서는 Invertible Residual Networks(i-ResNet)[27] 을 신경망 구조로 차용하였다. i-ResNet은 가역성과 Lipschitz 연 속성을 동시에 보장함으로써 광선 변환 네트워크의 표현 공간을 제한하고 해 공간(solution space)을 축소하여 문제의 불안정성 (ill-posedness)을 효과적으로 감소시킨다.
광선 변환 네트워크를 통해 구한 출사 광선들은 최종적으로 센서 평면에 투영되어 PSF를 형성한다. 본 연구에서는 [28]과 유사한 방식으로 PSF를 렌더링하였다. 구체적으로, 출사 광선으로부터 센서 평면에 투영된 점은 근처 픽셀에 영향을 주며 각 광선의 영 향을 모두 더하면 각 픽셀의 PSF 값을 구할 수 있다. 이를 수학적 으로 나타내면
와 같다. 여기서 p는 센서 평면 상 픽셀의 위치, rk는 샘플링된 입사 광선, L은 픽셀의 길이이다. g(rk)는 샘플링된 광선의 밀도 이다. σ(x)는 점의 영향을 정의하는 함수로, 픽셀 공간에서 픽 셀과 변위가 x인 점이 해당 픽셀에 미치는 영향을 나타낸다. 본 논문에서는 표준편차가 0.5인 가우시안 커널(Gaussian kernel)을 사용하였다. 이렇게 구한 PSF는 미분 가능하기 때문에 본 연구의 모델은 그래디언트 기반 알고리즘을 사용하여 종단간 방식으로 파라미터 최적화가 가능하다. Figure 1은 전체 렌더링 과정을 보 여준다.
4 실험
본 연구의 실험에서 렌즈는 double Gauss lens (이하 D-Gauss), Cooke triplet (이하 Cooke), Tessar를 사용하였다[29, p.312, p.133, p.202]. 센서의 해상도는 1024 × 1024로 설정하였으며, 물 체 거리 d와 포커싱 거리 f 의 경우 [13]과 유사하게각 값의 역수 가 동일 간격이 되도록 샘플링하였다. 모델 학습에 사용할 PSF는 심도 d를 {1, 1.5, 2}로 제한하고, 각 d 주변에서 블러 크기가 선 형적으로 변하도록 포커싱 거리 f 값을 9가지씩 선택한 뒤, 픽셀 위치는 9 × 9 균등 격자로 샘플링했다. 모델 평가에 사용할 PSF는 [1, ∞) 범위에서 다양한 d, f 와 더 세밀한 33 × 33 크기의 격자의 픽셀에서 선택하였다. 이는 비교적 희소하고 협소한 데이터로부 터 넓은 범위의 데이터를 보간 또는 외삽할 수 있는지를 확인하기 위함이다. 특히 실제 측정 시에는 멀리 있는(d가 큰) 점의 PSF를 구하는 것이 어려울 수 있다는 점을 고려한다.
광학계 모델과 PSF 렌더러는 JAX[30]를 사용하여 구현되었으며 최적화 과정에서 사용한 GPU는 NVIDIA Quadro RTX 5000이 다. 최적화 알고리즘으로는 Adam[31]을 사용하였다. 초기 학습 률(learning rate)은 10−3으로 설정하고 cosine decay scheduler을 사용하여 최종적으로 10−4까지 감소하도록 하였다. 배치 크기 의 경우, 4개의 (d, f)와 32개의 (x, y)를 샘플링하여 총 128개의 배치를 구성하였다. 모델 학습은 ‘초기 파라미터 탐색’과 ‘PSF 최적화’로 이루어지며 구체적인 내용은 다음에서 설명한다.
PSF 최적화 점광원의 PSF는 카메라와의 z축 방향 거리 d, 카메 라의 포커싱 거리 f, 점의 x, y 위치에 의존적인 값이다. 광학계를 재구성하기 위해서는 다양한 파라미터에 대한 PSF가 필요하다. 본 논문에서는 점의 x, y 위치의 경우 대응하는 이미지 픽셀의 위치로 대체하였다. 정확히는, 현재 카메라가 왜곡이 없는 이상 적인 투영을 가진다고 가정한 후 해당 점이 투영되는 센서 상의 픽셀의 위치를 파라미터 x, y로 사용하였다. 이는 물체의 거리에 상관없이 변하지 않기 때문에 다루기 수월하다.
모델 학습은 파라미터 (d, f, x, y)에 대한 모델의 PSF와 타겟 카 메라 PSF 간의 손실(loss)을 최소화하는 것으로 이루어진다. 이때 모델 PSF의 렌더링 위치는 타겟 PSF의 중심과 동일하게 설정하 며, 이에 모델은 왜곡에 따른 위치 변화를 고려하도록 학습된다. PSF는 타겟 카메라의 PSF 중 가장 높은 에너지(커널 성분의 총 합)를 가지는 PSF의 값으로 나누어 정규화하였다. 이때 PSF 간의 상대적인 밝기는 유지되므로 비네팅 역시 고려된다.
손실함수의 경우 PSF 간의 L1 거리인 ‘이미지 손실’과 더불 어 PSF의 총합 간 L1 거리인 ‘질량 손실’과 질량중심 간 L1 거 리인 ‘평균 손실’을 사용하였다. 이는 모델이 모든 광선을 차단 하여 PSF가 사라지는 등의 국소 최솟값(local minima)에 빠지는 것을 방지하기 위함이다. 일반적인 딥러닝 학습과 동일하게 최적 화에는 미니배치(minibatch)가 사용된다. 본 논문에서는 (d, f)와 (x, y)의 배치를 각각 샘플링한 후, 두 배치의 가능한 모든 쌍을 조합하여 최종 파라미터 배치를 만들었다.
초기 파라미터 탐색 PSF 최적화에는 적절한 초기 파라미터(initial parameter)가 필요하다. 만약 모든 광선이 차단되거나 엉뚱한 위치로 변화되는 등 모델이 타겟 카메라와 동떨어진 경우 PSF가 제대로 생성되지 않으며, 따라서 정상적인 최적화가 불가능하다. 따라서 본 논문에서는 초기 파라미터를 구하기 위해 앞서 두 번의 최적화 과정을 거친다.
첫 번째로, 카메라의 기본적인 정보를 토대로 근축광학(paraxial optics)에 기반한 타겟 카메라를 만들고 모델을 이에 맞춘다. 이때 타겟 카메라의 정보는 완전히 알려져 있으므로 PSF 최적화 대신 직접 함숫값 최적화로 광선 변환 모델을 맞춘다. 두 번째로, 카메라의 왜곡을 측정한 뒤, 모델의 왜곡이 이와 동일하도록 광선 변환 모델을 최적화한다. 이때 손실 함수는 모델이 생성한 스팟과 왜곡의 특징점(keypoint) 간의 평균제곱오차(mean squared error, MSE) 값이다. 이 과정 끝에 얻은 광학계 모델은 타겟 카메라에 정렬되어 PSF 최적화의 초기 파라미터로 적절하다.
본 연구의 방법은 기존 연구 [13]과 비교하였다. [13]에서는 왜곡 과 비네팅이 후처리로 보정된 상태에서 렌즈 블러의 PSF를 표현 하는 모델을 제안하였다. 모델은 물체 거리 d, 포커싱 거리 f 와 픽셀 위치(x, y), PSF 상 위치 (u, v)에 대한 PSF 값을 출력하는 함수로, 다층 퍼셉트론(multilayer perceptron, MLP)으로 구현되 었다. 하나의 PSF 커널을 생성하기 위해서는 PSF의 픽셀에 해 당하는 (u, v)를 격자 형태로 샘플링하여 모델에 투입 후 이차원 배열 형태로 변환해야 한다. 이 모델의 PSF와 타겟 카메라의 PSF 간의 MSE를 손실 함수로 하여 학습시켰다. 이때 원 논문과는다 르게 비네팅에 따른 밝기 차이를 보정하지는 않았다.
Table 1은 제시한 모델과 [13]의 학습 결과를 보여준다. 평가는 학습에 사용된 좁은 파라미터 범위의 학습용 PSF 세트와, 학습에 사용되지 않은 넓은 파라미터 범위의 검증용 PSF 세트를 사용하 였다. 학습용 PSF에 대한 성능은 [13]이 더욱 뛰어난 성능을 보 여준다. 그러나 검증용 PSF의 경우 [13]은 성능이 크게 떨어지는 반면 제안하는 모델(Ours)은 성능이 거의 유지된다.
| Training PSF (narrow) | Evaluation PSF (broad) | ||||
|---|---|---|---|---|---|
| Ours | [13] | Ours | [13] | ||
| D-Gauss | PSNR ↑ | 33.878 ± 6.354 | 35.903 ± 7.396 | 34.006 ± 6.006 | 23.140 ± 14.310 |
| SSIM ↑ | 0.953 ± 0.046 | 0.960 ± 0.037 | 0.956 ± 0.057 | 0.836 ± 0.177 | |
| Cooke | PSNR ↑ | 29.166 ± 5.808 | 36.040 ± 8.382 | 29.078 ± 5.830 | 25.991 ± 10.551 |
| SSIM ↑ | 0.879 ± 0.115 | 0.959 ± 0.041 | 0.880 ± 0.119 | 0.875 ± 0.147 | |
| Tessar | PSNR ↑ | 29.941 ± 5.666 | 37.146 ± 9.080 | 29.677 ± 5.544 | 26.093 ± 10.689 |
| SSIM ↑ | 0.896 ± 0.107 | 0.969 ± 0.036 | 0.889 ± 0.121 | 0.881 ± 0.160 | |
이는 두 방법의 동작 방식의 차이를 명확히 보여준다. [13]의 경우 높은 표현력의 MLP로 PSF를 바로 예측하기 때문에 주어진 데이터셋에 적합하는 것이 상대적으로 쉽다. 이 방법은 PSF의 광 학적 특성을 고려하지 않고 일반적인 회귀(regression)로 문제를 취급하기 때문에 데이터셋에 존재하지 않은 PSF를 적절히 보간 혹은 외삽할 수 없다는 한계가 있다. 반면 광학계 모델의 경우 PSF가 모델의 직접적인 출력이 아니므로 생성 과정이 복잡하여 주어진 데이터셋에 정확히 적합시키는 것이 어렵다. 그러나 적은 양의 PSF 세트만으로도 어느 정도 정확한 광학계 모델을 구성할 수 있다면, 학습 데이터와 무관하게 임의의 파라미터에 대한 PSF 를 상대적으로 정확히 구할 수 있는 장점이 있다.
Figure 2는 학습 데이터에 포함되지 않은 멀리 떨어진 점(d = 10m)에 대한 PSF 렌더링 결과를 비교한다. 제시한 모델의 경우 대체로 타겟 PSF와 유사한 형태를 가지며 강도의 범위도 정상 적이다. 반면 [13]의 경우 타겟 PSF의 강도 범위를 크게 벗어나 실제로 유의미하게 사용되기 어렵다.
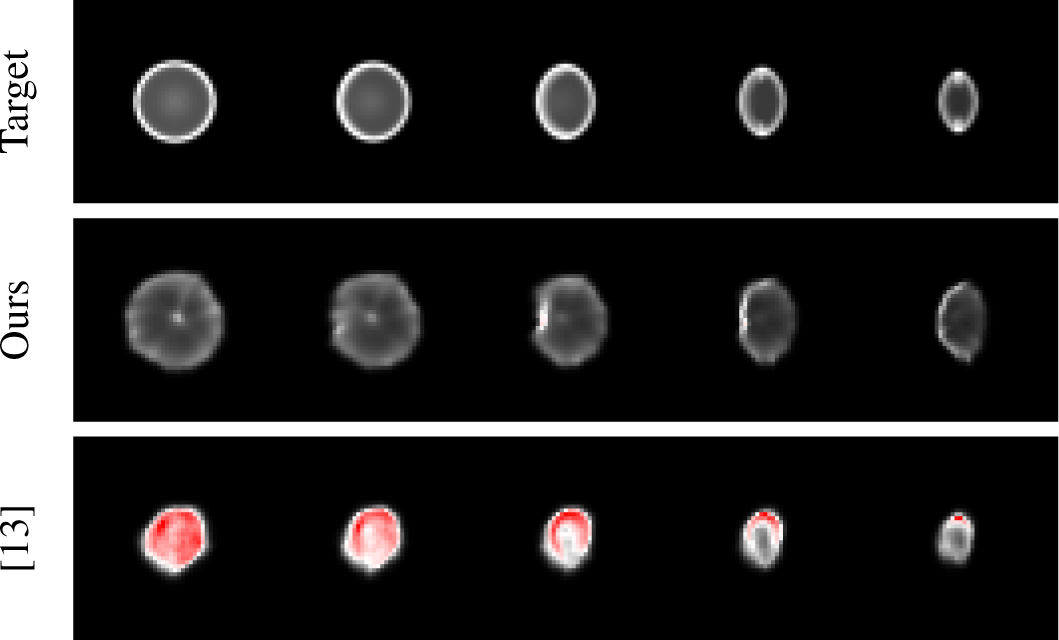
Table 2는 렌더링 결과를 보여준다. [13]에서 제시한 캘리브레 이션 패턴 이미지를 타겟 렌즈와 각 모델로 렌더링한 후 비교하 였다. 이때 파라미터 범위는 검증용 데이터셋과 동일하다. [13] 의 경우 PSF의 밝기를 적절히 예측하지 못하므로 밝기 보정(illumination correction)을 하지 않은 경우 완전히 잘못된 결과를 보인다. 밝기 보정을 한 경우에는 어느 정도 동작하나 정확도가 높지 않다. 반면 본 연구에서 제안한 모델의 경우 전반적인 정확 도가 더 뛰어나며, 모델에 밝기 정보가 내재되어 있으므로 밝기 보정이 없더라도 좋은 성능을 보인다. Figure 3은 밝기 보정 없 이 렌더링한 예를 보여준다. [13]의 경우 전반적인 PSF의 밝기가 떨어져 타겟 이미지보다 어둡게 렌더링되었다.
| Without illumination correction | With illumination correction | ||||
|---|---|---|---|---|---|
| Ours | [13] | Ours | [13] | ||
| D-Gauss | PSNR ↑ | 35.296 ± 3.386 | 9.407 ± 2.585 | 36.634 ± 4.329 | 26.546 ± 4.500 |
| SSIM ↑ | 0.979 ± 0.021 | 0.361 ± 0.251 | 0.980 ± 0.021 | 0.829 ± 0.181 | |
| LPIPS ↓ | 0.146 ± 0.018 | 0.496 ± 0.301 | 0.143 ± 0.017 | 0.095 ± 0.070 | |
| Cooke | PSNR ↑ | 34.754 ± 3.571 | 8.978 ± 2.392 | 35.533 ± 4.262 | 28.101 ± 4.862 |
| SSIM ↑ | 0.973 ± 0.035 | 0.361 ± 0.249 | 0.973 ± 0.035 | 0.873 ± 0.174 | |
| LPIPS ↓ | 0.020 ± 0.028 | 0.471 ± 0.304 | 0.020 ± 0.028 | 0.064 ± 0.064 | |
| Tessar | PSNR ↑ | 26.034 ± 5.018 | 8.224 ± 2.602 | 26.281 ± 5.218 | 27.185 ± 4.661 |
| SSIM ↑ | 0.805 ± 0.115 | 0.365 ± 0.253 | 0.805 ± 0.115 | 0.872 ± 0.166 | |
| LPIPS ↓ | 0.142 ± 0.106 | 0.455 ± 0.289 | 0.141 ± 0.106 | 0.065 ± 0.073 | |

Figure 4는 D-Gauss 렌즈를 타겟으로 학습한 결과이다. 각 이미지 는 특정 (d, f)에 대한 PSF를 여러 픽셀 위치 (x, y)에서 보여준다. 학습된 모델의 PSF는 정밀도가 매우 높은 것은 아니지만 대체로 타겟의 PSF를 잘 모사하고 있다. 모델의 PSF 렌더링은 타겟 카 메라와 동일한 위치, 밝기 스케일로 이루어졌다. 즉, 왜곡과 밝기 보정을 따로 적용하지 않았다. 따라서 학습된 모델이 블러의 모양 뿐 아니라 왜곡, 비네팅 역시 반영한다고 볼 수 있다.

네트워크 구조Table 3은 광선 변환 모델의 구조로 i-ResNet이 아닌 일반 MLP를 사용하였을 때 결과를 보여준다. MLP는 선형 계층과 계층 사이 ReLU를 활성화 함수로 사용한 기본적인 구조 이다. Table 3에서 ‘MLP (4x32)’는 차원이 32인 중간 계층 4개를 가지는 MLP를 뜻하며, i-ResNet과 거의 같은 개수의 파라미터 를 가진다. ‘MLP (6x64)’는 차원이 64인 중간 계층 6개를 가지는 MLP이며, 앞의 모델보다 많은 파라미터를 가진다.
| #Params | PSNR ↑ | SSIM ↑ | |
|---|---|---|---|
| i-ResNet | 3480 | 34.006 ± 6.006 | 0.956 ± 0.057 |
| MLP (4x32) | 3460 | 23.022 ± 4.091 | 0.519 ± 0.201 |
| MLP (6x64) | 21 380 | 21.406 ± 4.261 | 0.400 ± 0.222 |
실험 결과 일반 MLP의 경우 i-ResNet에 비해 최적화 결과가 크 게 떨어졌다. 또한 규모가 더 큰 MLP가 오히려 작은 것보다 낮은 성능을 보여주었다. 이로부터 낮은 성능의 원인은 MLP의 표현 능력의 한계가 아니라 떨어지는 학습 안정성임을 짐작할 수 있 다. 이에 i-ResNet의 구조에 내재된 제약 조건이 모델 최적화에서 중요하게 작용한다고 볼 수 있다.
위치 인코딩Table 4는 차단 함수의 위치 인코딩에 따른 결과를 보여준다. 인코딩에 따른 차이가 두드러지게 나타나지는 않으나, 인코딩 차수가 4인 경우가 다른 경우보다 약간 우세함을 알 수 있다. 위치 인코딩이 없는 경우(N = 0) 불연속적인 함수 표현이 불리하여 성능이 약간 떨어지는 것으로 볼 수 있다. 반면 차수가 너무 높을 경우(N = 8) 인코딩된 입력값의 변화가 급격해져 학 습의 안정성을 떨어뜨리는 것으로 추측된다.
| PSNR ↑ | SSIM ↑ | |
|---|---|---|
| N = 0 | 33.903 ± 5.921 | 0.954 ± 0.058 |
| N = 4 | 34.006 ± 6.006 | 0.956 ± 0.057 |
| N = 8 | 33.958 ± 6.052 | 0.955 ± 0.058 |
5 논의
본 논문에서 제시한 모델이 가지는 이점을 정리하면 다음과 같 다. 첫째, 여러 특성을 하나의 모델로 통합함으로써 더 간편하고 압축적인 모델을 제시한다. 둘째, 광학계의 특성을 활용함으로써 적은 양의 측정 데이터만으로 다양한 파라미터에 대한 블러 등의 특성 예측(보간 및 외삽)이 가능하다. 최적화 성능을 개선한다면 본 연구의 방법은 실제로 더욱 유용하게 활용될 수 있을 것이라 생각하며, 개별 특성(블러, 왜곡 등)을 측정하는 도구를 넘어 광 학계 모델 자체를 필요로 하는 작업에도 사용될 수 있을 것이다.
제안한 모델은 빛의 파동적 성질을 고려하지 않는다는 한계가 있다. 렌즈의 F-number가 큰 경우 회절이 PSF에 유의미한 영향 을 주므로, 이를 무시하면 모델의 정확도가 떨어질 수 있다. 이를 보완하기 위해 렌더링된 PSF에 조리개 형태에 따른 회절무늬를 컨볼루션(convolution)하여 별도로 적용하거나, 출사 광선을 평 면파로 가정하여 근사적인 파동광학적 효과를 모사하는 방법을 고려할 수 있다. 또한, 본 모델은 광선이 광학계의 각 요소를 순 차적으로 통과함을 가정하지만, 실제 복합렌즈에서는 렌즈 표면 에서의 내부 반사에 의해 일부 광선은 순차적인 경로를 따르지 않는다. 이는 렌즈 플레어(lens flare) 등의 복잡한 현상을 일으킨 다. 본 모델은 이러한 효과를 반영하지 못하므로, 이에 대한 추가 연구가 필요하다.



