발산 제약 이동최소제곱법을 이용한 평활화된 입자 유체역학 기반 벡터장 설계

1 서론

이동최소제곱법(Moving Least Squares, MLS)은 흩어진 데이터 를 부드럽게 근사하거나 고차로 보간하는 데 널리 사용되는 기법 이다. 확률 밀도 함수에 MLS를 적용하면 보다 정확한 분포 추정 이 가능해지기 때문에, 유체 시뮬레이션 [1, 2], 변형체 모델링 [3], 메시화 [4, 5] 등 다양한 분야에서 활용되고 있다. 다항식 보간은 샘플 지점 간의 값을 추정하는 데 사용되며, 연속적인 물질의 움 직임을 표현해야 하는 유체 시뮬레이션이나 캐릭터 모델링에서 특히 중요하다. 이때 적절한 보간 방식의 선택은 결과 품질에 직 접적인 영향을 미친다 [6,7,8].

물리 기반 시뮬레이션에서 보간을 통한 샘플링 데이터 추정 은 핵심적인 과정이다. 기하 처리 분야에서는 점군(Point Cloud) 데이터로부터 메시 표면을 근사 생성하는 데 이 기법이 사용 된다. 점군 데이터는 연결 정보가 없기 때문에, 고차 수치 기 법을 통해 암시적으로 삼각형 기반 메시를 생성해야 한다 [4]. 물리 시뮬레이션에서도 시뮬레이션 정확도를 향상시키기 위 해 고차 보간 기법이 자주 사용된다 [9]. 예를 들어, 연기 시 뮬레이션에서 이류(advection) 항에 사용되는 선형 보간 기반 의 세미-라그랑주(Semi-Lagrangian) 방법 [10]을 개선하기 위해 BFECC(Back and Forth Error Compensation and Correction)[11], CIP(Constrained Interpolation Profile)[12], USCIP(Unsplit Semi-Lagrangian CIP)[13], 스트림 기반 연기[14], 주파수 기반 난 류 [15], 적응형 와류 기법 [16], Polynomial PIC [17] 등의 다양한 방법이 제안되었다.

Feldman 등은 적응형 격자 구조에서 부드러운 벡터장을 얻기 위해 속도의 수직 성분(normal component)을 기반으로 MLS를 계산하였다 [18]. 이처럼 MLS는 고차 보간을 위한 유용한 도구 이지만, 연속성 조건이나 물리적 제약조건을 충족시키기 어려워 실제 시뮬레이션에서는 활용에 제약이 있다. 이를 해결하고자, Hong 등은 발산 제약 기반 MLS(Divergence-Constrained MLS)를 제안하였으며, 이는 포아송 방정식을 푸는 과정을 생략하면서도 유체와 유사한 움직임을 갖는 벡터장을 생성할 수 있게 한다 [6]. 이 기법은 연기 시뮬레이션에 적용되어 복잡한 난류 현상을 효과 적으로 재현하였다 [7].

본 연구에서는 밀도 기반 입자 데이터로부터 벡터장을 시각화 하기 위한 새로운 접근으로 몬테카를로 가중치를 적용한 MLS 기법을 제안한다. Figure 1은 기존 MLS와 Hong et al.이 제안한 발산 제약 MLS 간의 벡터 보간 차이를 보여준다 [6]. Figure 1a 는 서로 반대 방향의 벡터 두 개를 제약 조건으로 사용하여 MLS 를 적용한 결과이며, Figure 1b는 발산 제약 기반 MLS를 활용해 생성한 벡터장이다. 발산 제약 기반 MLS는 비압축성을 만족시 키는 보간 기법으로, 유체 시뮬레이션에 적합한 특징을 지닌다 (Figure 1b 참조). 일반적인 MLS와 비교했을 때 벡터장 구조에서 뚜렷한 차이를 보이며(Figure 1a 참조), 발산 조건을 통해 다양한 형태의 벡터장을 설계할 수 있다는 장점이 있다.

Figure 1: In comparison to the standard MLS vector interpolation, the pseudo-divergence-free vector interpolation [6].

Download Original Figure

하지만, 이 방식은 격자 공간에서 벡터 제약만을 고려하기 때 문에 오일러(Eulerian) 기반 시뮬레이션에만 적용이 가능하다는 한계가 있다. 이를 보완하기 위해 본 논문에서는 SPH 접근법을 통해 입자 밀도가 분포하는 위치를 추정하고, 이 위치와 주변 입 자 간의 거리를 MLS 내 추가 가중치로 반영함으로써 SPH 입자 데이터의 분포를 고려한 벡터장 시각화를 가능하게 한다.

2 관련 연구

유체 시뮬레이션 분야에서는 난류의 시각적 세부 묘사를 향상시 키기 위해 다양한 이류(Advection)와 외력(External force) 기법 들이 활발히 연구되어 왔다 [19,20,10]. 대표적으로 세미 라그 랑지안 방법은 유체의 안정적인 시뮬레이션을 위해 고안되었으 며 [10], 와류 제한(Vorticity confinement) 기법은 격자 기반 환경 에서 난류의 와류 힘을 효과적으로 추정하여 적용하였다 [21]. 이후 라그랑지안 입자를 와류 전달 매개체로 사용하는 와류 입 자법으로 발전하는 과정을 거쳤다 [22]. 그 외에도 BFECC [11], CIP [12], USCIP [13], 스트림 기반 연기 표현 [14], 주파수 기반 연기 [15], 적응형 와류 기법 [16], 그리고 Polynomial PIC [17] 등 여러 기법들이 제안되어 왔다.

특히 입자 기반 시뮬레이션을 통해 서브그리드(Subgrid) 수준 의 유체 디테일을 강화하려는 시도도 많았다. Kim et al.[23]과 Losasso et al.[24]는 SPH(Smoothed Particle Hydrodynamics) 모 델을 도입하여 서브그리드 스플래시 현상을 효과적으로 처리하 였다. 다상 유체의 정밀한 표현을 위해 입자 혼합 모델을 제안한 연구로는 Greenwood와 House [25], Hong et al.[26], Thuerey et al.[27]의 사례가 있으며, Gao et al.은 라그랑지안 입자를 활용해 기체 흐름의 고속 특성을 포착하는 연구를 수행하였다 [28]. 또 한, 서브그리드 역학에 물리 모델을 결합함으로써 다상 인터페이 스 [29], 화염의 주름 현상 [30, 31], 그리고 액체 표면의 세밀한 디테일을 더욱 향상시키는 연구가 이어졌다 [32]. Hong et al.은 발산 제한 MLS 방법을 개발하여 푸아송 방정식의 계산 없이도 유체 움직임을 효과적으로 표현하는 방식을 제안하였다 [6]. 이 기법은 이후 연기 시뮬레이션 내 이류 과정에 통합되어 난류 표현 에 활용되었으나 [7], MLS 기반 난류는 디테일보다는 노이즈가 두드러져 시뮬레이션 제어가 어렵고, 고차 방정식으로 인한 계산 비용이 커 산업적 적용에는 제한이 따른다.

이와는 별개로, 후처리 단계에서 유체 흐름의 디테일을 보강 하는 방법들도 연구되고 있다. 웨이블릿 노이즈 [33]와 컬 노이 즈 [34, 35] 같은 노이즈 함수를 활용해 저해상도 시뮬레이션에 난류 움직임을 합성하는 접근이 대표적이다. 최근에는 Chu와 Thuerey가 합성곱 신경망을 이용해 저해상도와 고해상도 유동 사이의 관계를 학습하는 연구를 진행했다 [36]. 또한 Sato et al. 은 패치 기반 텍스처 합성 기법을 통해 저해상도 유체 흐름에 난 류 디테일을 효과적으로 전달하는 방법을 제안하였다 [37]. Chen et al.은 연속체 역학과 MLS를 결합하여 종이와 유체의 상호작용 및 찢김 현상을 동시에 시뮬레이션하는 통합적인 프레임워크를 개발하였다 [38]. 그러나 이러한 후처리 기법들은 노이즈 함수 기 반 특성상 실제 고해상도 시뮬레이션보다 유동의 사실감이 다소 떨어지는 한계가 있다.

MLS를 SPH 기반 유체 시뮬레이션의 경계 처리에 직접 적용한 연구도 있다 [39]. SPH 시뮬레이션에서는 일반적으로 경계 입자 (boundary particle)를 활용해 경계를 처리하지만, 평면에 가까운 경계에서는 노이즈가 섞인 불규칙한 움직임이 발생하는 문제가 있었다. 이를 개선하기 위해 MLS를 적용하여 노이즈 없이 보다 부드럽게 경계를 처리했으나, MLS를 경계 처리에만 사용했기 때문에 다양한 벡터장을 직접 생성하거나 설계하는 데는 한계가 있다.

본 연구에서는 MLS 가중치 산출에 SPH 기법을 활용하고 있으 나, SPH가 다양한 분야에서 널리 사용되는 샘플링 기법임을 밝 힌다. Yu et al.이 제안한 비등방성 형태의 SPH 커널을 계산하여 이를 MLS에 통합함으로써 [40], SPH 입자의 속도가 수치적으로 소실되거나 과도하게 스무딩되는 문제를 완화할 수 있다. 이로 인해 본 방법은 SPH 기반 속도장 설계뿐만 아니라, 물리 기반 시 뮬레이션에서 나타나는 난류 모델링에도 효과적으로 적용할 수 있다.

3 제안하는 프레임워크

본 논문에서는 제안하는 발산 제약 기반의 MLS 기법을 소개하기 에 앞서, 먼저 스칼라 및 벡터 보간을 위한 기본적인 MLS 방법에 대해 설명한다. 이후, ‘SPH 비등방성 가중치 기반 MLS’ 장에서는 SPH 기법을 활용하여 비등방성 가중치를 계산하고, 이를 MLS 프레임워크에 통합하는 방식을 제안한다. 이 과정을 통해 최종적 으로 벡터장을 효과적으로 구성할 수 있는 방법론을 제시한다.

Figure 2는 본 논문에서 제안하는 SPH 입자 기반 방법으로 계 산된 벡터장을 시각화한 것이다. 그림의 왼쪽에 있는 빨간색 점은 제약 입자를 나타내며, 제약 벡터가 주어졌을 때 제안하는 기법을 통해 해당 벡터장 전체가 자동으로 생성되는 과정을 보여준다. 일반적으로 SPH 방식은 커널 함수로 인해 주변 입자의 속도가 소실되거나 과도하게 스무딩되는 경향이 있으나, 본 방법은 주변 입자의 속도를 제약 벡터로 설정함으로써 보다 난류적인 형태를 효과적으로 표현할 수 있다.

Figure 2: Algorithm overview of our method.

Download Original Figure

3.2 SPH의 비등방성 가중치를 이용한 발산제약 기 반 이동최소제곱

3.2.1 확산 미분

이번 절에서는 확산 도함수(diffuse derivative) 개념과 몬테카를 로 기반 가중치를 사용하는 MLS(Moving Least Squares) 기법을 중심으로 설명한다. 우선 함수 f 의 정확한 미분 값을 얻기 위해 수식 1을 미분하면 다음과 같은 결과를 얻을 수 있다 (수식 11 참고).

$$\frac{\partial f}{\partial \text{x}}=\frac{\partial {\text{b}}^T}{\partial \text{x}}{\text{c+b}}^T\frac{\partial \text{c}}{\partial \text{x}}$$

(11)

위 표현에서 첫 번째 항은 비교적 간단하게 계산 가능하지만, 두 번째 항은 c의 위치 의존성을 고려해야 하므로 계산 복잡도 가 급격히 증가한다. 따라서 이를 실질적인 MLS 프레임워크에 통합하기 어려운 측면이 있다. 이러한 복잡성을 회피하기 위해, 두 번째 항을 확산 도함수로 대체하면 근사적으로 충분한 정확 도의 미분 값을 계산할 수 있으며, 전체 계산의 효율성을 높일 수 있다 [6] (수식 12).

$$\frac{\partial f}{\partial \text{x}}\simeq \frac{\partial {\text{b}}^T}{\partial \text{x}}\text{c}$$

(12)

확산 도함수를 활용하면 벡터장 u에 대해 발산 연산자인 $\nabla \cdot \text{u=}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}$ 을 보다 간단한 방식으로 근사할 수 있으며, 그 결과는 다음과 같다 (수식 13).

$$\nabla \cdot \text{u}\simeq \frac{\partial {\text{b}}^T}{\partial x}{\text{c}}_x+\frac{\partial {\text{b}}^T}{\partial \text{y}}{\text{c}}_y+\frac{\partial {\text{b}}^T}{\partial z}{\text{c}}_z$$

(13)

3.2.2 Divergence 제약 조건

Huerta 등은 ∇·u = σ 형태의 발산 제약식을 활용하여, 특히 σ = 0일 때 비압축성 유동에 대한 해석 정확도를 향상시켰다 [41]. 본 연구에서는 σ를 비제로 값으로 설정할 수 있도록 하여, 속도장의 보간에서 발산 정도를 정밀하게 조절할 수 있게 하였다. 이를 위 해 기존의 벡터 보간 행렬인 B_vec에 발산 제약 항을 결합하며, 이 과정에서 수식 13을 다음과 같이 재구성한다 (수식 14).

$$\nabla \cdot \text{u}\simeq {\text{b}}_{div}^T\left(\text{x}\right)\cdot \text{c}$$

(14)

여기서 b_div는 다음 방식으로 구성된다 (수식 15).

$$\begin{array}{ll}{\text{b}}_{div}\left(x\right)\hfill & =\frac{\partial \left[{\text{b}}^T\left(\text{x}\right)00\right]}{\partial x}+\frac{\partial \left[\text{0}{\text{b}}^T\left(\text{x}\right)0\right]}{\partial y}+\frac{\partial \left[\text{0}0{\text{b}}^T\left(\text{x}\right)\right]}{\partial z}\hfill \\ \hfill & =\left[\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}00\right]+\left[0\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}0\right]+\left[00\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial z}\right]\hfill \\ \hfill & =\left[\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial z}\right]\hfill \end{array}$$

(15)

이때 b의 편미분은 각 기저함수 항에 대해 독립적으로 계산되 며, 예를 들어 d = 3, m = 2일 경우 다음과 같은 형태를 갖는다 (수식 16).

$$\begin{array}{ll}\frac{\partial \text{b}\left(\text{x}\right)}{\partial x}\hfill & =\left[0,1,0,0,2x,0,0,y,0,z\right]\hfill \\ \frac{\partial \text{b}\left(\text{x}\right)}{\partial y}\hfill & =\left[0,0,1,0,0,2y,0,x,z,0\right]\hfill \\ \frac{\partial \text{b}\left(\text{x}\right)}{\partial z}\hfill & =\left[0,0,0,1,0,0,2z,0,y,z\right]\hfill \end{array}$$

(16)

이제 위의 발산 조건 ${\text{b}}_{div}^T\cdot \text{c=}\sigma$를 기존 MLS 시스템(수식 9) 에 결합하면, 발산 제약을 반영한 MLS 방정식을 얻을 수 있다 (수식 17).

$${\text{W}}_{div}\left(\text{x}\right){\text{B}}_{div}{\text{c}}_{vec}\left(\text{x}\right)={\text{W}}_{div}\left(\text{x}\right){\Phi }_{div}$$

(17)

이 방정식 역시 앞서 소개한 최소자승 기법을 통해 안정적으로 풀 수 있으며, 본 논문에서 사용하는 전체 시스템의 구성은 다음 과 같다:

$${\text{W}}_{div}=\left[\begin{array}{c}{\text{W}}_{vec}\\ {\omega }_{div}\end{array}\right],{\text{B}}_{div}=\left[\begin{array}{c}{\text{b}}_{vec}\\ {\omega }_{div}\end{array}\right],{\Phi }_{div}=\left[\Phi ,\sigma \right].\text{여기서}$$

W_div는 (dN + 1) × (dN + 1)이고, Wdiv ∈ R(dN +1)×(dN +1)는 가중 대각 행렬이다. 또한 Bdiv ∈ R(dN +1)×dk 는 계수 행렬이며, Φ_div ∈ RdN +1는 보간 타겟 값을 포함하는 벡터이다.

3.2.3 평활화된 입자 유체역학 기반 비등방성 가중치

우리는 얇은 시트를 감지하기 위해 비등방성 커널 방법을 활용한 다 [40]. 이를 위해 먼저 입자들의 가중 평균 공분산 C를 다음과 같이 계산한다 (수식 18).

$$C_i=\frac{{\displaystyle \sum {}_j\left({\text{x}}_j-{\text{x}}_i^w\right){\left({\text{x}}_j-{\text{x}}_i^w\right)}^{T}W\left({\text{x}}_j-{\text{x}}_i^w,h\right)}}{{\displaystyle \sum {}_{j}W\left({\text{x}}_j-{\text{x}}_i^w,h\right)}}$$

(18)

여기서 x_i는 타겟 입자, 그리고 x_j는 인접 입자들이며, W 는 SPH 시뮬레이션에서 일반적으로 사용하는 등방성 커널 함수이다. 이 값들을 기반으로 $x_i^w$ 는 다음과 같이 계산한다 (수식 19).

$${\text{x}}_i^w=\frac{{\displaystyle \sum {}_j{\text{x}}_{j}W\left({\text{x}}_j-{\text{x}}_i,h\right)}}{{\displaystyle \sum {}_{j}W\left({\text{x}}_j-{\text{x}}_i,h\right)}}$$

(19)

연관된 C_i에 대해 특이값 분해(Singular Value Decomposition, SVD)를 수행하면, 주변 입자 위치의 방향성과 신장 정도를 각각 고유벡터와 고유값의 형태로 얻을 수 있다 (수식 20).

$$C_i=\text{C=R}\Sigma {\text{R}}^T={\left[\begin{array}{c}{\text{e}}_1^T\\ {\text{e}}_2^T\\ {\text{e}}_3^T\end{array}\right]}^T\left[\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right]\left[\begin{array}{c}{\text{e}}_1^T\\ {\text{e}}_2^T\\ {\text{e}}_3^T\end{array}\right]$$

(20)

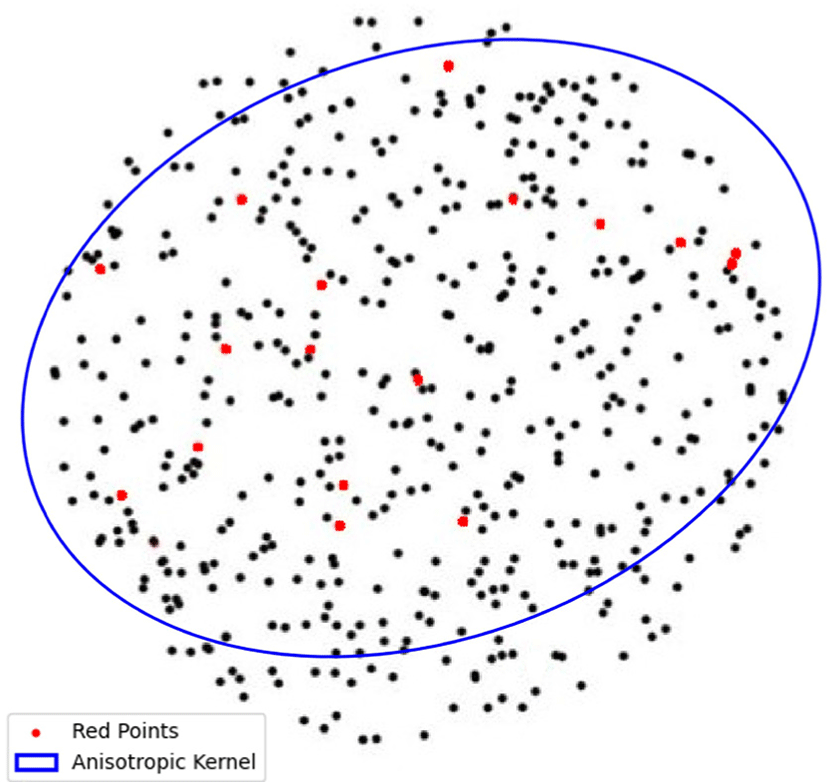
여기서 e_n과 σ_n은 각각 분산의 크기와 신장 정도에 따라 정렬 된 주축과 고유값을 의미한다. SVD는 α₁ρ₀ < ρ(x_i) < α₂ρ₀인 경우에만 적용되며, 그 외의 경우에는 diag(σ,σ,σ)= I를 사 용한다. 본 논문에서는 α₁은 0.05, α₂는 0.7로 설정하여 사용했으 며, 이 값은 실험을 통해 얻어진 값이다. 이후, 우리의 기법은 G_i 를 다음과 같은 형태의 대칭 행렬로 구성한다 (수식 21). Figure 3 은 무작위로 배치된 SPH 입자들에서 비등방성 가중치를 타원체 형태로 시각화한 결과이다. 본 논문에서 사용하는 발산 제약 기 반 MLS에서는 제약 벡터의 영향이 크기 때문에, 이를 가중치에 반영하기 위해 그림에 붉은색 점으로 표시된 제약 입자들만을이 용해 비등방성 가중치를 계산하였다.

Figure 3: Anisotropic ellipse fitting to red points.

Download Original Figure

$${\text{G}}_i=\frac{1}{h}\text{R}{\Sigma }^{-1}{\text{R}}^T$$

(21)

이렇게 계산된 선형 변환 행렬 G를 이용하여 비등방성 커널을 계산한다 (수식 22).

$$\Gamma \left({\text{x}}_i\right)=\underset{i}{\min }\left(\Vert {\text{G}}_i\left({\text{x}}_j-{\text{x}}_i\right)\Vert \right)$$

(22)

SPH 기반 비등방성 가중치를 통해 MLS 가중치인 ω^* (|r_i|)를 구성하는 방법은 다음과 같다 (수식 23).

$$\omega *\left(\left|{\text{r}}_i\right|\right)=\omega \left(\left|{\text{r}}_i\right|\right)\Gamma \left({\text{x}}_i\right)$$

(23)

여기서 ω (|r_i|)는 노드와 제약 노드 간의 거리를 계산한 가중치 이고, Γ (x_i)는 입자 간의 비등방성 가중치이며, 이 값들을 통해 가중치 행렬인 W를 구성하여 MLS를 계산한다.

4 실험 결과

본 연구의 결과들을 만들기 위해 실험한 환경은 Intel Core i7-7700K CPU, 32GB RAM, Geforce GTX 1080Ti GPU가 탑재된 컴퓨터를 이용하였다. 본 논문에서 보여주는 결과는 2차원 SPH 입자들을 가진 데이터를 통해 벡터장을 표현했다.

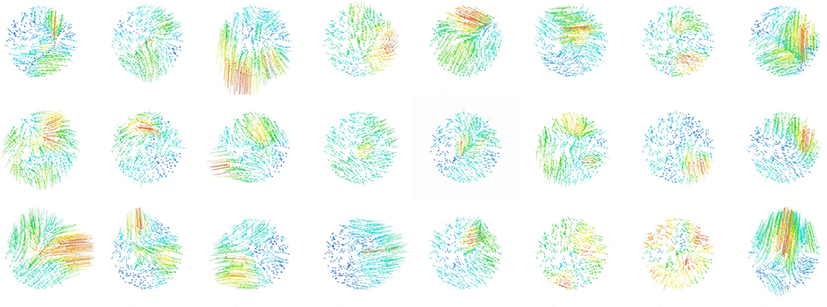
Figure 4는 2차원 공간에 SPH 입자들을 무작위로 배치한 후, 제약 노드를 포함한 장면에서 벡터장을 추출한 결과이다. 제약 노드에 해당하는 입자는 매 프레임마다 무작위로 선택되도록 설 정했으며, 제약 벡터 또한 임의로 결정되도록 실험을 구성하였 다. 이는 본 논문에서 제안하는 방법이 특정 장면에만 국한되지 않고, 다양한 무작위 환경에서도 안정적으로 작동함을 입증하기 위함이다. 실험 결과, 모든 장면에서 안정적인 벡터 흐름이 형성 되었으며, 이에 따른 벡터장도 자연스럽게 생성되는 양상을 확인 할 수 있었다.

Figure 4: Various types of vector fields generated using our method based on SPH particle simulations.

Download Original Figure

5 정성적 평가

본 논문에서는 SPH 기반 입자 데이터를 활용하여 다양한 벡터장 패턴을 생성하는 기법을 제안했다. 특히 발산 제약 조건을 포함한 MLS 프레임워크에 SPH의 비등방성 커널을 통합함으로써, 기존 격자 기반 방법이나 일반 MLS 보간 방식으로는 표현하기 어려운 세밀한 벡터 흐름을 효과적으로 시각화할 수 있음을 보였다.

Figure 4에서는 본 연구에서 제안한 기법을 통해 생성된 다양 한 벡터장의 형태가 시각적으로 제시되어 있다. 실험은 2차원 공 간에 SPH 입자들을 무작위로 배치한 후, 각 프레임마다 제약 노 드를 임의로 선택하고 제약 벡터 또한 랜덤하게 설정하여 수행 되었다. 이러한 구성은 특정한 조건이나 장면에 종속되지 않고, 다양한 초기 상태에서도 제안 기법이 안정적으로 작동할 수 있는 지를 평가하기 위한 목적을 지닌다.

실험 결과, 제약 조건이 무작위로 주어졌음에도 불구하고 생 성된 벡터장들은 전체적으로 부드럽고 자연스러운 흐름을 유지 하였으며, 입자 분포의 불균일성과 관계없이 구조적인 일관성을 갖춘 형태로 표현되었다. 이는 제안된 방법이 특정 장면에만 국 한되어 작동하는 것이 아니라, 다양한 환경에서도 일관된 결과를 생성할 수 있는 범용성과 알고리즘적 안정성을 확보하고 있음을 정성적으로 입증하는 결과라 할 수 있다.

6 결론 및 향후 연구

본 논문에서는 SPH의 분산된 입자 데이터를 고려하여, MLS 기 반으로 벡터장을 생성하는 새로운 방식을 제안하였다. 제약 조건 만 입력으로 주어지면 다양한 패턴의 벡터장을 표현할 수 있기 때문에, 본 방법은 벡터 디자인이나 속도장이 요구되는 모델링 및 시뮬레이션 분야에 활용될 수 있다.

현재 결과는 난류가 고려된 벡터장을 표현할 수 있는 가능성을 보여주고 있지만, 이를 실제 물리 기반 시뮬레이션에 적용하기 위해서는 연속성을 갖는 벡터장으로 생성되도록 알고리즘의 개 선이 필요하다. 단순히 생성된 벡터장을 외력으로 적용할 경우 노이즈처럼 작용할 가능성이 높으며, CFL 조건을 조절함으로써 일정 부분 해결할 수는 있으나, 이는 결과적으로 힘의 크기를 줄 이는 방식이기 때문에 근본적인 해결책이 되기 어렵다. 향후에는 이러한 문제들을 개선할 수 있도록 연구를 지속적으로 확장해 나 갈 계획이다.