1 서론
얼음은 자연계에서 가장 흔하게 볼 수 있는 고체 상태의 물질중 하나로, 그 생성 과정과 시각적 특성은 온도, 압력, 용존 기체의 농도, 냉각 속도 등 다양한 인자에 의해 결정된다. 이러한 물리적 다양성 덕분에 얼음은 오랫동안 컴퓨터 그래픽스 분야에서 중요 한 연구 대상이 되어 왔다. 특히 고드름이나 종유석처럼 길이와 형태가 변화하는 결빙 성장(freezing growth), 그리고 빛의 산란 특성에 기반한 투명·불투명 얼음 렌더링은 사실적인 자연 현상 표현의 핵심 주제로 다뤄져 왔다.
그러나 기존 연구의 대부분은 형태 제어나 렌더링 표현에 초 점을 두었으며, 결빙 과정에서 실제로 발생하는 열역학적 상전이 (phase transition) 와 내부 기체 운동 같은 물리적 동역학 현상은 충분히 다루어지지 않았다. 예를 들어, Im et al.과 Kim은 입자-격 자 하이브리드(particle-grid hybrid) 기법을 활용해 불투명 얼음의 내부 공기 방울(air bubbles)과 용존 산소 분포(dissolved oxygen field)를 모델링하고, 이를 언리얼 엔진(Unreal Engine)으로 렌더 링하는 효율적 기법을 제안하였다 [1, 2]. 하지만 이러한 접근은 냉각 과정이 완료된 후의 정적 상태(static state)에 초점을 맞추고 있으며, 냉각 도중 발생하는 급격한 열 확산, 증기화, 그리고 재결 정(recalescence) 과정에서의 자기-점프(self-jumping) 현상과 같 은 비평형적 거동은 포함하지 않는다.
물리적으로 self-jumping은 급속한 결빙 동안 내부의 재결정 발 열(release of latent heat) 과 증기화 모멘텀(evaporative impulse) 이 외부로 방출되면서, 얼음 방울이 미세한 반작용 힘을 받아 순 간적으로 튀어 오르는 현상이다. 이러한 거동은 실험적으로도 확 인되었지만, 그래픽스 시뮬레이션에서는 이를 표현할 모델이 거 의 존재하지 않았다. 기존 모델들은 열전달 방정식이나 용존 공기 확산 모델을 기반으로 정적인 얼음 형태를 재현할 수 있었으나, 결빙 중 비선형 에너지 전이와 운동 반응을 직접적으로 시각화하 지는 못하였다.
이에 본 연구에서는 결빙 과정에서 발생하는 재결정 유도 자 기-점프(Self-Jumping) 현상을 시각적으로 모델링하기 위한 경량 입자 기반 시뮬레이션 프레임워크를 제안한다. 제안 기법은 온도 장의 국소적 불안정성과 공기 방출의 비대칭성을 단순화된 물리 모델로 추상화하여, 실제 물리 실험에서 관찰되는 점프 방향성과 속도 스케일을 재현한다. 또한 사용자는 환경 압력, 냉각 비율, 임펄스 누적 시간창 등 파라미터를 조정함으로써 다양한 형태 의 결빙 및 점프 거동을 직관적으로 제어할 수 있다. 본 연구는 기존의 정적 렌더링 중심 얼음 시뮬레이션을 넘어, 결빙 자체가 시각적 사건으로 작동하는 새로운 물리 기반 시뮬레이션 모델을 제시한다.
2 관련 연구
컴퓨터 그래픽스에서 얼음은 주로 형상 성장(icicles, speleothems)과 광학적 표현(불투명·산란 렌더링)을 중심 으로 연구되어 왔다. Gagnon et al.은 유수와 표면 에너지 균형을 절차적으로 근사해 상호작용형 고드름 생성을 제안했고 [3], 동굴 석순·석순 성장(스펠레오템)을 물리-화학 모델로 모사해 장면 규모의 애니메이션까지 확장하는 접근도 보고되었다 [4]. 보다 폭넓게는눈·얼음 애니메이션 전반을 정리한 최신 SOTAR 가 존재하며, 입자/격자 하이브리드, 위상장(phase-field) 기반 동결 패턴 등 그래픽스 기법의 계보를 정리한다 [5].
한편 불투명 얼음의 내부 기포 방향성까지 포함하는 효율적 모 델링·렌더링도 제안되었다 [2]. 이 계열 연구는 정적 결과물(형 상·광원 응답)을 고품질로 생성하는 데 강점이 있지만, 재결정·증발 등 비평형 열-유체 현상이 이끄는 동역학적 사건(예: self-jumping)은 범위 밖으로 남아 있다.
재결정(recalescence) 단계는 과냉각수(supercooled water)에서 핵생성 후 잠열 방출로 액적 온도가 급상승하는 현상으로, 이어 지는 증발 플럭스 증가와 결합해 압축-변형 후 이탈(jumping)을 유도할 수 있음이 보고되었다. Graeber et al.은 재결정 중의 온도 급상승과 얼음 레비테이션/이탈 메커니즘을 정량화했고 [6], 최 근 Yan et al.은 저압(∼100 Pa)에서의 동결 방울이 증기화 모멘텀 (vaporization momentum) 때문에 과압(overpressure) 가설보다 크 게 점프를 유발함을 실험·이론·수치로 입증했다 [7]. 또한 확장 맥락에서, 확산/결정화가 동반된 동결 스프레딩의 재결정 단계를 단계적으로 기술한 유체역학 연구도 존재한다 [8].
이 선행들은 핵생성 위치(θn) 와 전선(Front) 전파가 증발 플럭 스의 시공간 분포를 비대칭화하고, 그 적분 임펄스가 점프 방향 (≈ −θn) 과 강도를 좌우한다는 점에서, 본 연구의 자동 핵생성과 아크 제한 임펄스 누적 전략에 물리적 근거를 제공한다.
증기화 모멘텀은 재결정 구간의 표면에서 증발 질량유량×법선 방향으로 생성되는 반작용 성분으로, 동결 방울의 self-jumping 임펄스를 설명한다 [7]. 점프 메커니즘 자체는 동결에 한정되 지 않으며, 응결/응축계(coalescence) 에서도 표면장 에너지 이 득→운동 에너지 전환으로 방울이 이탈하는 coalescence-induced jumping이 잘 알려져 있다 [9, 10, 11]. 또한 저압 환경이 점프 고 도/속도를 유리하게 만드는 실험적 결과도 다수 보고되었다 [12]. 다만 이들 유체역학 연구는 표면장 또는 재결정-증발에 의한 임 펄스의 물리를 중심으로 하며, 그래픽스 워크플로 측면—임의 실 루엣, 인터랙티브 파라미터 제어, 분리 이후 원본 형상 보존 강 체화 등—은 다루지 않는다. 본 연구는 이를 보완해 제작 입자 파이프라인으로 방향성 임펄스 누적→분리 판정→강체 전환을 연결한다.
3 물리 기반 결빙 및 Self-Jumping 현상 개요
과냉각된(supercooled) 물방울이 결빙을 시작하면, 내부에서 잠 열(latent heat)이 방출되며 온도가 순간적으로 상승하는 재결정 (recalescence) 현상이 발생한다. 이 과정에서 표면의 열적 불균일 성과 증발 압력의 차이가 비대칭적으로 나타나면서 방울이 스스 로 이탈하는 self-jumping 현상이 발생한다. 이러한 현상은 실제 저압 환경의 실험에서도 관찰되지만, 그래픽스 분야에서는 시각 적으로 재현되거나 모델링된 사례가 거의 없었다.
본 연구에서는 이 self-jumping 현상을 단순화된 물리 모델을 기반으로 시뮬레이션하여, 결빙 과정에서 나타나는 비대칭적인 열적 반응과 증기화에 의한 반작용 힘을 시각적으로 표현할 수 있는 프레임워크를 제안한다. 제안된 모델은 복잡한 열역학 방정 식이나 CFD 해석 없이도, 핵생성(nucleation)→재결정 전선 확산 (front propagation)→열 안정화(thermal clamp)→방향성 임펄스 누적(impulse accumulation)→강체 점프(rigid jump)로 이어지는 물리적 과정을 간결하게 재현한다.
특히 입자 기반(particle-based) 접근을 통해 각 입자의 온도와 상(phase) 상태를 추적하며, 표면 냉각 편향(cooling bias)이나 임 펄스 누적 시간창(impulse window) 등 물리적으로 해석 가능한 파라미터를 사용한다. 이로써 물리 현상의 본질은 유지하면서도, 그래픽스 제작자가 직관적으로 제어할 수 있는 경량의 시각 시뮬 레이션이 가능하다.
결과적으로, 본 연구의 프레임워크는 “재결정 기반 결빙→열 적 비대칭→방향성 임펄스→점프 동역학” 으로 이어지는 self-jumping의 물리적 연쇄 과정을 시각적, 동역학적 측면에서 간단 하고 효율적으로 모델링한다.
4 제안하는 프레임워크
이번 절에서는 제안 파이프라인(2D 입자 기반 결빙 → 재결정 → 임펄스 누적 → 강체 전환)의 절차를 상세히 기술한다. 핵심은 (1) 표면 온도장의 임계 도달로 자동 핵생성, (2) 재결정 밴드 안정 화, (3) 전선 주변 아크 제한(Arc-limited) 영역에서 방향성 임펄스 누적, (4) 임계 충족 시 강체 전환과 원본 형상 보존이다. 상세한 알고리즘을 설명하기에 앞서, Table 1에서는 본 논문 전반에서 사용되는 주요 기호와 물리적 매개변수를 정리하였다.
먼저 중심 C ∈ ℝ2를 기준으로 반경 R의 원판 영역에, 균일 간격 s로 입자 를 배치한다 (see Figure 1). 각 입자는 초기 온도 Ti = Tinit에서 시작하며, 액상비는 αi = 1로 두어 액체 상태(Liquid)임을 명시한다. 표면 법선은 중심 방향을 따라 ni = normalize(xi − C)로 초기화한다.
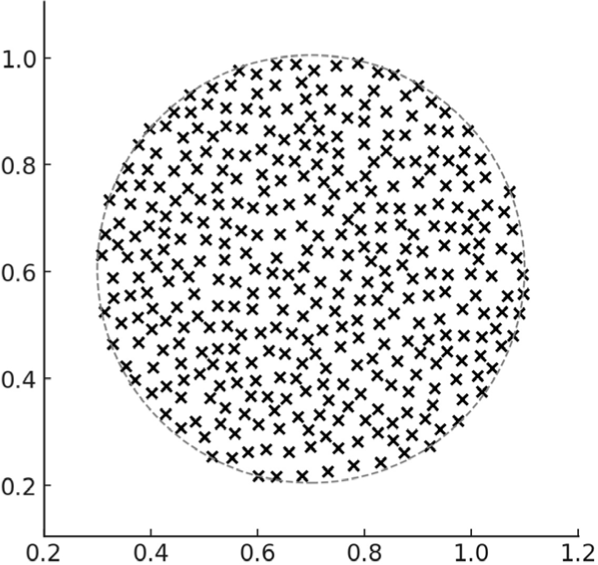
인접한 상호작용을 효율적으로 계산하기 위해, 반경 h 내에 위 치한 이웃을 입자별 리스트로 유지한다. 입자 i의 이웃 집합은 다음과 같이 정의한다 (see Equation 1).
결빙 전 단계에서 각 입자의 위치는 단순히 물리적 좌표 집합일 뿐, 어떤 입자가 실제로 외부에 노출된 표면 인지 판별하기 위해 서는 국소 밀도에 기반한 추가적인 검출 과정이 필요하다. 본 연 구에서는 입자 주변의 수밀도(Number density)를 측정하여 표면 여부를 결정한다. 이를 위해 널리 사용되는 2차원 Poly6 커널을 적용하여, 입자 i의 근방에 위치한 이웃 입자들의 공간적 분포를 다음과 같이 이웃 입자들의 합으로 근사한다 (see Equation 2).
여기서 r = ∥xj − xi∥은 두 입자 간 거리이며, (·)+ 연산자는 음수 구간에서 0으로 클램프되는 양의 부분 함수를 의미한다. 즉, r > h인 경우 커널의 값이 0이 되어, 이웃 반경 h를 넘어서는 입자들의 영향은 자동으로 제거된다.
모든 입자에 대해 계산된 수밀도 {ni} 중 상위 10%의 평균값을 nref로 두고, ni < ς·nref인 입자를 표면으로 분류한다. 여기서 ς 는 사용자가 입력한 가중치로 본 논문에서는 0.82로 설정했다. 이 방식은 외곽 입자들이 내부보다 주변 이웃 수가 적다는 점을 이용 한 간단하지만 효과적인 표면 검출 기준이며, 특히 비정형 입자 분포나 포아송 샘플링 기반 배치에서도 안정적으로 동작한다.
표면이 판정된 후에는 표면으로부터 내부로의 거리 기반 위상 정보를 구축하기 위해 너비 우선 탐색(Breadth-First Search, BFS) 을 이용해 각 입자에 레이어 인덱스를 부여한다. 표면 입자는 레 벨 0으로 시작하고, 이웃 탐색을 통해 인접한 내부 입자들에게 순차적으로 증가하는 정수 레벨을 지정한다 (see Equation 3).
이렇게 얻어진 레이어 구조는 이후 단계에서 얼음 껍질의 커버 리지 계산 및 내부 전파(Propagation) 판정의 기준으로 사용되어, 결빙이 진행됨에 따라 표면으로부터 내부로 확장되는 동결 거동 을 효율적으로 추적할 수 있다.
핵생성(Nucleation)은 결빙 초기 단계에서 결정이 처음 형성되는 물리적 과정으로, 표면의 국소 냉각 속도와 열적 불균일성에 의 해 결정된다. 본 연구에서는 외부에서 인위적인 핵(Seed)을 부 여하지 않고, 표면 입자들의 온도 분포가 시간에 따라 진화함에 따라 자발적 핵생성(Auto-nucleation)이 발생하도록 설계하였다. 즉, 표면 온도장 Ti가 임계 과냉각(Critical supercooling) 조건에 가장 먼저 도달하는 위치를 핵생성 지점으로 정의한다.
이를 위해 매 시뮬레이션 프레임마다 Schrage 근사를 기반으 로 한 증발 냉각 모델을 적용한다. Schrage 근사는 표면과 주변 환경 간의 증기 압력 차이에 비례하여 질량 플럭스가 발생한다고 가정하며, 이를 통해 표면 온도의 시간 변화율을 근사적으로 표 현할 수 있다. 입자 i의 온도 감소량은 다음과 같이 계산된다 (see Equation 4).
여기서 Jw(Ti)는 온도 Ti에서의 물 표면 증발 플럭스, kcool은 냉 각 계수, β는 표면 법선 ni가 상부 방향 ŷ와 이루는 각도에 따라 냉각을 가중하는 상부(y) 편향 계수이다. 이 항은 실제 중력장 하 에서 상부 표면이 하부보다 더 빠르게 냉각되는 경향을 모사하기 위한 것이다. 본 논문에서 β는 0.3으로 설정했다.
Figure 2는 본 연구에서 사용된 표면 냉각 편향 함수의 각도 의존성을 나타낸다. 가로축은 표면 법선의 극각(0◦ → x 방향, 90◦ → y 방향)을, 세로축은 냉각 가중치 1+β max (0, ni·ŷ 를 각 각 의미한다. 상부(y) 방향을 향하는 표면일수록 외부로의 증발이 활발해지므로, 해당 영역의 냉각 속도가 상대적으로 커지는 현상 을 모사한다. β = 0.3일 때, 법선이 y축을 향하는 부근(90◦ 근처) 에서 최대 약 1.3배의 냉각 강화 효과가 나타나며, 하부 영역(y 방 향)은 편향이 거의 없는 1.0 수준으로 유지된다. 이 편향 모델은 저압 환경에서의 실제 물리적 현상, 즉 중력 방향 상부의 표면이 하부보다 빠르게 온도를 잃고 먼저 결빙이 시작되는 경향을 단순 화하여 표현한다. 세로축을 나타내는 냉각 가중치의 기본 구조는 표면 법선이 위쪽(y) 방향을 향할수록 냉각이 강해진다는 물리적 근거(자연 대류·증발 편향)를 반영한 것이다. 즉, 위쪽 표면일수록 공기 흐름과 접촉이 많아지고, 증발 플럭스가 상대적으로 커지는 경향을 단순 모델을 표현한 것이다. 냉각 가중치에서 사용하는 β에 0.3을 대입했을 때 1 + 0.3 max (0, ni·ŷ) ≈ 1.0 to 1.3 범위를 갖게 된다. 따라서 1.3배의 냉각 강화 효과는 모델 파라 미터로부터 계산된 수치적 결과이지, 실험 데이터에서 직접 얻은 값은 아니다.
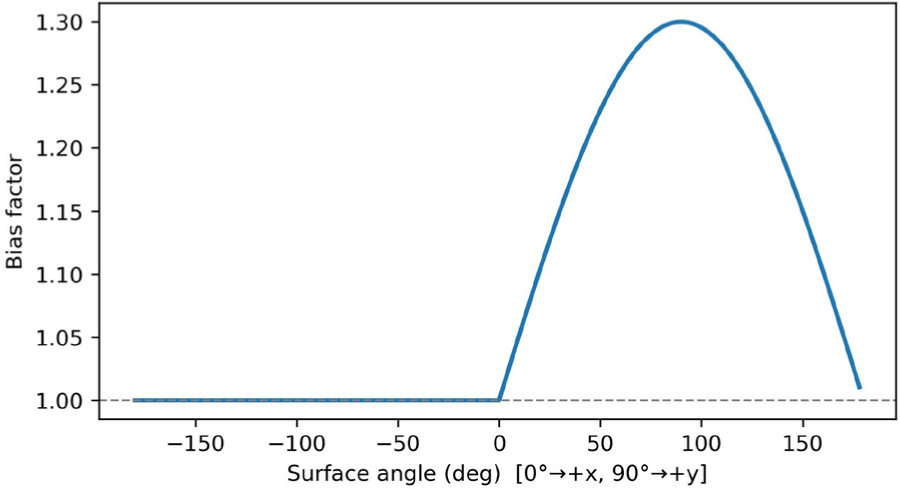
시간이 경과함에 따라 표면 입자들은 점진적으로 냉각되며, 그 중 일부는 다음 임계 조건을 만족한다 (see Equation 5).
여기서 Tm은 물의 융점(0◦C), ∆Tnuc은 핵생성을 유도하는 과 냉각 임계값이며, 본 논문에서는 ∆Tnuc = 12로 설정한다. 임계 온도는 아래와 같이 정의하고 (see Equation 6), 시간 t에서 표면 집합 S에 속한 입자들의 최소 온도를 다음과 같이 둔다 (see Equation 7).
이때 핵생성은 다음의 최초 시점 tnuc에서 자동으로 발생한다 (see Equation 8).
이때 핵생성 지점이 되는 입자 인덱스 i*는 아래와 같이 계산하 고 (see Equation 9), 만약 수치적 이유(동일 온도, 소수점 반올림 등)로 동률이 발생하면, 다음의 우선순위를 적용해 하나를 선택 한다: (1) 최근 프레임 구간에서의 냉각률이 더 큰 입자, (2) 상향 법선 성분이 더 큰 입자(ni·ŷ가 큰 순), (3) 인덱스가 작은 입자 (결정적 결정).
핵생성 씨드의 위치 각도는 중심 C에 대한 극각으로 정의한다 (see Equation 10).
여기서 xi*는 씨드 입자의 좌표이다.
핵생성 이벤트가 확정되면, 시뮬레이션 상태 변수를 True로 전 환하고, 전선(Front) 전파 및 임펄스 누적 단계의 초기 조건을 다 음과 같이 설정한다.
이 초기화는 재결정 전선의 양/음 방향 전파가 씨드 각 θseed 에서 동시에 시작되도록 보장하며, 이후 (6)–(10)의 정의에 따라 전선 확산, Mushy 밴드 온도 안정화, 아크 제한 임펄스 적분, 분리 (Detach) 판정이 순차적으로 진행된다. 요약하면, (8)–(9)에 의해 가장 먼저 임계 과냉각에 도달한 표면 입자가 자동으로 씨드로 선택되며, 그 각도 (10)를 기준으로 전선 확산 단계가 시작된다.
이 절차를 통해 외부 입력 없이도 온도장의 동적 분포에 의해 핵생성 위치와 시점이 자동으로 결정된다. 특히, 이 접근법은 저 압 환경에서 실험적으로 관찰된 비대칭적인 초기 결빙 패턴—즉, 특정 표면 방향에서 먼저 재결정이 시작되는 현상을 간단한 열-증발 모델로 재현할 수 있다는 점에서 실용적이다.
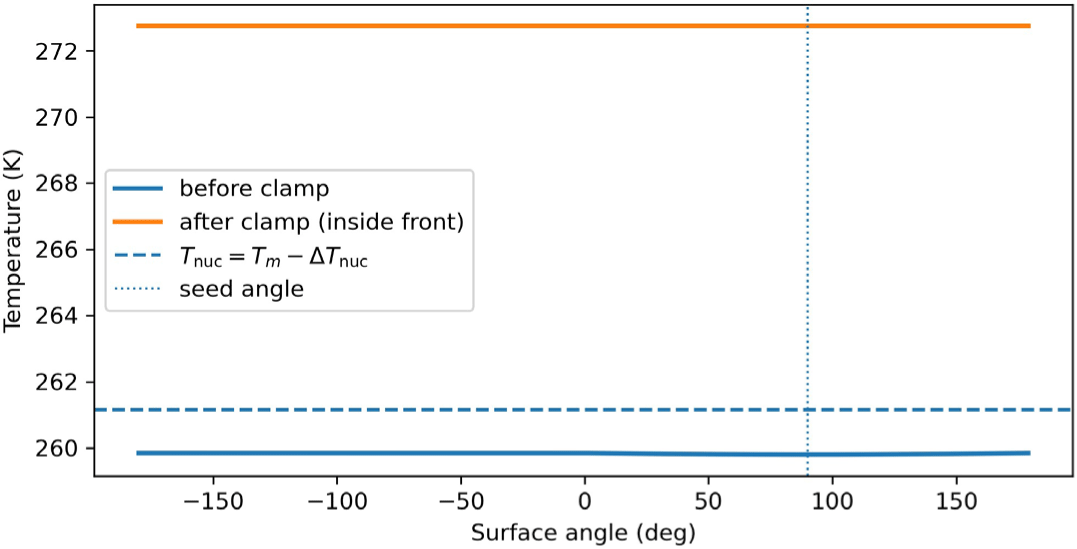
Figure 3은 표면 각도에 따른 온도 분포의 시간적 변화를 나 타낸다. 파란색 곡선은 초기 상태에서의 균일한 표면 온도 Ti = Tinit를, 주황색 곡선은 냉각 모델을 40 프레임 동안 적용한 뒤 의 온도 분포를 각각 보여준다. 점선은 핵생성 임계온도 Tnuc = Tm − ∆Tnuc 을 표시하며, 이 값에 먼저 도달한 위치가 자동 핵생 성(Auto-nucleation)의 시작점이 된다.

그래프에서 볼 수 있듯이, 상부(y 방향)에 해당하는 각도(약 90◦ 부근)의 입자들이 가장 빠르게 냉각되어 Tnuc 이하로 먼저 도 달하고, 해당 지점이 첫 번째 씨드로 선택된다. 이는 앞서 제시된 냉각 편향 모델(see Figure 2)이 예측한 바와 같이, 상향 표면에서 증발이 더 활발하게 일어나며 열 손실이 크게 발생하기 때문이 다. 따라서 Figure 3은 본 연구의 자동 핵생성 알고리즘이 편향된 냉각 조건 아래에서 실제 물리적 현상과 일관된 시각적 결과를 재현함을 보여준다.
덧붙여, Figure 3의 곡선이 각도에 따라 거의 일정해 보이는 이유는 초기 온도가 균일하고, 편향 계수 β가 작으며(본 실험에 서는 β = 0.3), 적분 시간(40 프레임)이 짧아 상부(y) 편향 항 1+ β max(0, ni·ŷ)에 따른 온도 차이가 축 스케일 대비 매우 작기 때문이다. β를 크게 하거나(예: 1.0 이상), 적분 프레임 수를 늘리 면(예: 200 프레임) 상부 근처(약 90◦)에서 더 뚜렷한 하강 곡선을 확인할 수 있다.
Figure 4는 원형 표면을 따라 분포한 입자들의 온도장과 자동 핵생성(Auto-nucleation)이 발생한 씨드 위치를 시각적으로 보여 준다. 색상은 각 표면 입자의 온도 값을 나타내며, 색상 막대는 절 대온도(K) 기준으로 표기하였다. 상부(y) 방향의 입자들이 더 낮 은 온도를 가지며, 이 영역에서 처음으로 임계온도 Tnuc = Tm − ∆Tnuc 에 도달함을 확인할 수 있다. 빨간색 원으로 표시된 입자 는 이러한 임계 조건을 가장 먼저 만족한 핵생성 지점으로, 이후 재결정 전선(Recalescence front)의 확산이 해당 방향으로 시작 된다.
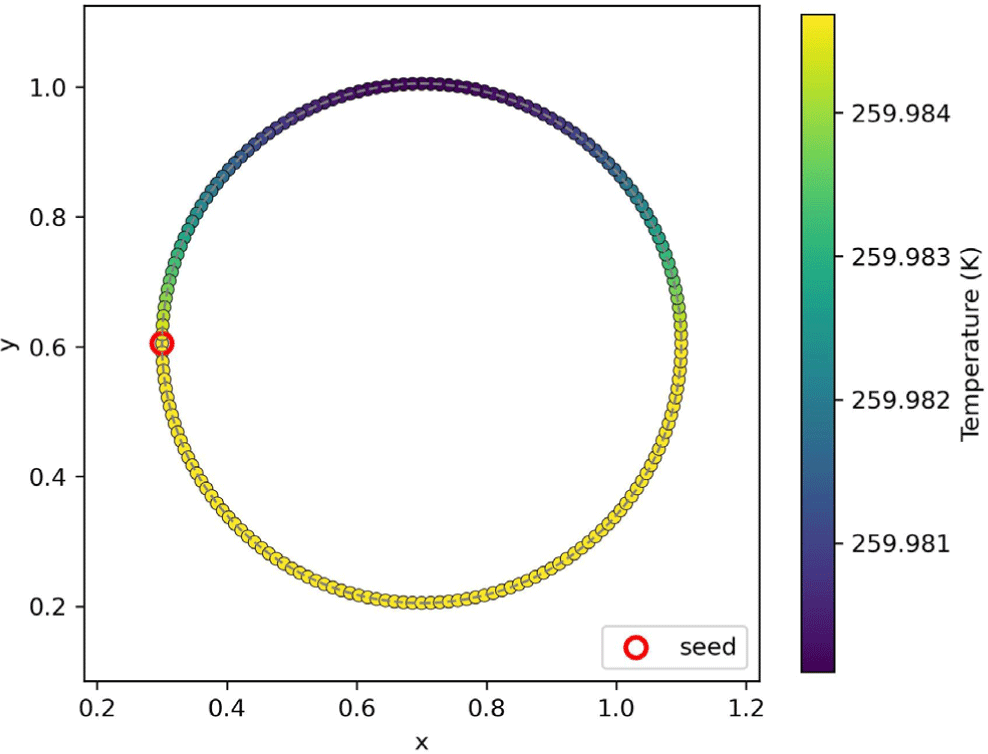
이 결과는 앞서 제시한 냉각 편향 모델(see Figure 2)과 온도 분포 시뮬레이션(see Figue 3)에서 예측된 경향과 일치한다. 즉, 상향(y) 표면에서의 증발 냉각이 더 강하게 작용하여 결빙이 먼 저 시작되고, 그 위치가 실제 자동 핵생성의 출발점으로 작동함 을 보여준다. 따라서 본 그림은 단순한 열–증발 모델을 통해 실제 저압 환경에서 관찰되는 비대칭적 결빙 개시 현상을 효과적으로 재현함을 입증한다.
본 논문에서는 결빙 과정을 기술하기 위해 세 가지 용어를 명확히 구분하여 사용한다. (1) 전선(front)은 재결정이 퍼져나가는 이동 경계선을 의미하며, (2) 재결정 밴드(recalescence band)는 전선이 지나간 직후의 열적 과도구간, (3) Mushy band는 액–고체가 공존 하며 상변화가 진행되는 부분 고상화 층이다.
핵생성이 시작된 이후에는 결정화 경계(Front)가 씨드 각도 θseed를 중심으로 양방향으로 확산되며 표면을 따라 전파된다. 이 전선의 이동은 결빙 속도의 비대칭성과 열적 확산에 의해 결정되 며, 시간에 따라 다음과 같이 기술할 수 있다 (see Equation 14).
여기서 vpos/neg는 각각 전선이 씨드의 양의 방향과 음의 방향으 로 퍼져 나가는 각속도를 의미한다.
Figure 5은 재결정 전선(Front)의 전파 범위를 표면 각도에 따 라 나타낸 것이다. 파란색 실선은 시뮬레이션의 최종 시점에서 전선이 도달한 각도 범위를 의미하며, 점선은 씨드가 위치한 초기 핵생성 각도 θseed를 표시한다. 그래프가 전 구간에서 1로 일정하 게 유지되는 것은, 설정된 전선 속도 vpos/neg와 시뮬레이션 시간 (tfinal)이 충분히 커서 전체 표면이 재결정 전선의 영향권에 포 함되었음을 의미한다. 즉, 시간 경과에 따라 전선이 양방향으로 완전히 확산되어 표면 전역이 결빙(Front coverage = 1.0) 상태에 도달한 결과이다. 이 단계는 이후의 온도 안정화(see Figure 6) 및 액상비 감소(see Figure 7)로 이어지는 초기 조건을 형성하며, 재 결정 전선의 완전 확산이 결빙 껍질(Freezing shell, 부분 고상화 껍질) 형성의 전제 단계임을 시각적으로 확인할 수 있다.
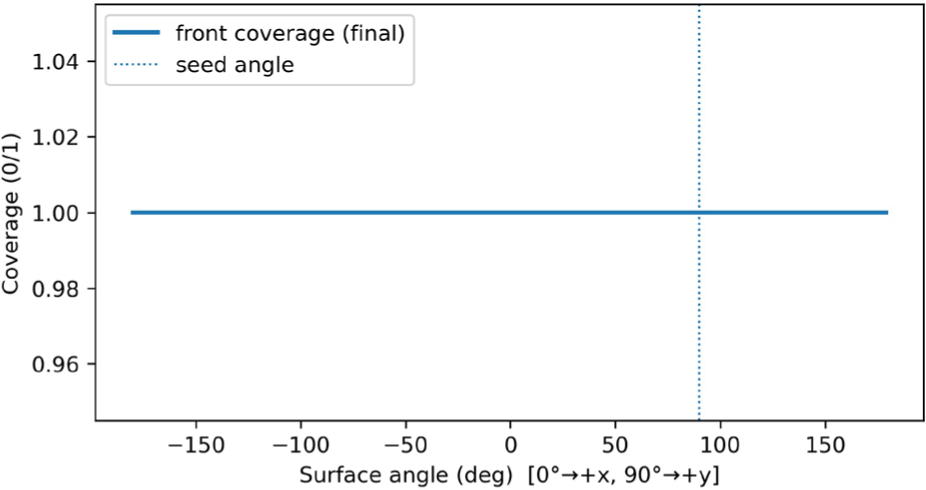
각 입자 i의 위치 각도 θi에 대해 di = angwrap(θi − θseed) 로 정의하고, |di|≤ θpos (또는 θneg)를 만족하면 그 입자는 현재 재결정 전선 내부에 포함된 것으로 간주한다. 이 구간의 입자들 은 고상(Solid)으로 완전히 전이되기 전, 액상과 고상이 공존하는 Mushy band 상태로 존재하며, 온도는 0◦C 근방으로 제한된다. 이 때의 온도 안정화 과정은 다음과 같이 클램프 연산으로 표현된다 (see Equation 15).
재결정 밴드의 존재는 실제 물리 과정에서 나타나는 잠열(Latent heat) 방출 구간을 단순화하여 모델링한 것이다.
본 논문에서는 전선 뒤에서 Mushy band와 부분 고상화가 진행 분히 경과하여 완전히 고체(Solid) 상태가 된 최종 껍질층을 고상 껍질(Solid shell)로 구분한다.
Figure 6은 결빙이 진행된 후 표면 각도에 따른 온도 분포를 나타낸다. 파란색 실선은 클램프 연산 적용 이전의 온도 분포를, 주황색 실선은 재결정 전선 내부에 대해 클램프가 적용된 이후 의 온도 분포를 각각 보여준다. 점선은 핵생성 임계온도 Tnuc = Tm − ∆Tnuc을, 세로 점선은 씨드가 위치한 각도를 나타낸다.
그래프에서 확인되듯이, 클램프 연산 후 전선 내부의 온도 가 0◦C 근방으로 제한되며 온도 변동이 급격히 억제된다. 이는 Mushy band 구간에서 발생하는 잠열(Latent heat) 방출을 수치 적으로 단순화한 결과로, 고상(Solid)과 액상(Liquid)이 공존하는 영역의 열적 안정화(Thermal stabilization) 효과를 재현한다. 또한 그래프가 전 구간에서 일정한 형태를 보이는 것은 시뮬레이션에 서 설정된 클램프 폭 wm이 작고, 시뮬레이션 시간이 짧아(40 프 레임) 각도에 따른 온도 차이가 미소하기 때문이다. 시뮬레이션 시간을 늘리거나 wm을 크게 하면 상부(+y) 방향의 온도가 빠르 게 클램프 구간에 진입하는 경향이 더 뚜렷하게 나타난다. 따라서 Figure 6은 재결정 전선이 확산된 이후의 온도장이 Mushy band 모델에 의해 수치적으로 안정화되고, 이 과정이 고상 껍질(Solid shell)의 형성을 위한 초기 조건으로 작용함을 보여준다.
즉, 급격한 온도 상승을 억제하고, 주변 입자들과의 열적 평형 을 유지하면서 결정화가 연속적으로 확산될 수 있도록 한다. 또한 이 구간에서 각 입자의 액상비 αi는 점진적으로 감소하며 고상으 로의 전이를 표현한다 (see Equation 16).
여기서 kα는 상변화율(Phase transition rate)을 의미한다.
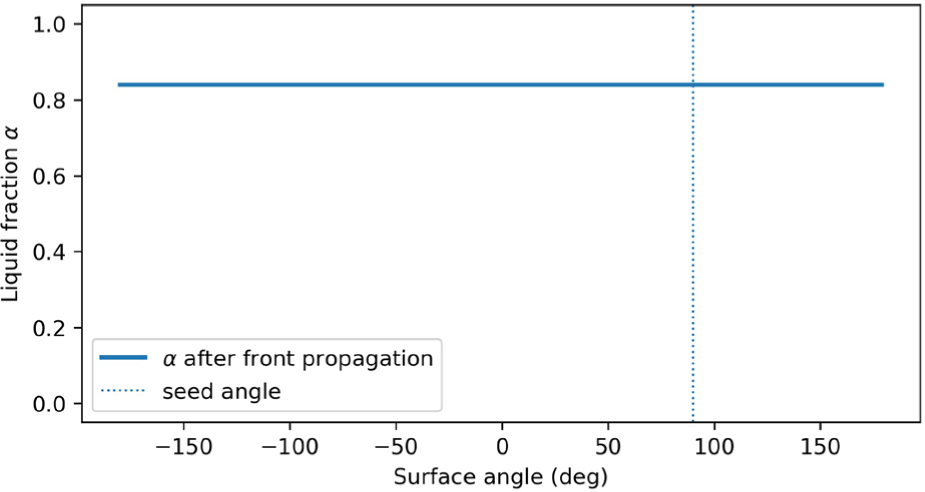
Figure 7은 재결정 전선(Front) 전파 이후의 표면 각도에 따른 액상비(Liquid fraction) αi의 분포를 보여준다. 파란색 실선은 전 선이 통과한 이후 각 입자의 액상비를 나타내며, 세로 점선은 씨 드가 위치한 각도를 표시한다.
그래프에서 대부분의 영역이 α ≈ 1.0을 유지하는 것은 재결 정 전선이 충분히 확산되었으나, 시뮬레이션 시간(40 프레임)이 짧고 상변화율 kα 값이 작아 실제 액상에서 고상으로의 전이가 부분적으로만 진행되었기 때문이다. 또한 α가 1보다 약간 감소 한 영역은 전선(Front)에 의해 이미 결빙이 진행된 구간으로, 이 구간에서 입자들은 Mushy band를 거쳐 고상(Solid)으로 서서히 전이한다. 따라서 본 그림은 Mushy band 모델을 통해 고상 전 이의 공간적 범위와 속도를 간단히 표현할 수 있음을 보여준다. 결과적으로, 액상비의 점진적 감소는 재결정 전선 뒤에서 결빙 껍질(Freezing shell)이 형성되는 과정을 정성적으로 잘 반영하고 있다.
결과적으로 재결정 전선은 씨드로부터 시작되어 표면을 따라 비대칭적인 속도로 확산되며, Mushy band를 통한 온도 안정화 덕분에 결빙 전파가 수치적으로 안정적이고 연속적으로 표현된 다. 이 단계는 이후의 고상 껍질(Solid shell) 형성과 임펄스 축적 단계로 이어지며, 자발적 self-jumping 현상의 전제 조건이 된다.
Self-jumping 현상의 근본적인 원인은 재결정 구간(얼음 또는 Mushy 표면)에서 발생하는 증발 플럭스 Ji와 액체 표면에서의 증 발 플럭스 Jw의 불균형으로부터 기인한다. 이 차이는 표면 법선 방향으로 반작용 임펄스(Reaction impulse)를 발생시키며, 시간 에 따라 누적될수록 droplet 전체에 순수한 운동량 변화를 일으켜 결국 자발적인 점프(Jump)를 유도하게 된다.
그러나 모든 방향의 플럭스를 동일하게 적분하면 상반된 수평 성분들이 서로 상쇄되어 실제 점프 방향성이 소멸될 수 있다. 따 라서 본 논문에서는 전선(Front) 주변의 얇은 아크(Arc) 영역만을 선택적으로 적분함으로써, 임펄스의 수평 성분 상쇄를 최소화하 고 실제 물리적 점프 방향을 재현하였다. 이 과정을 수식으로 표 현하면 다음과 같다 (see Equation 17).
여기서 A는 아크 형태의 적분 영역을 의미하며, 즉 입자 i가 차지하는 대표 면적이며, 일반적으로 입자 간격의 제곱에 비례한 다 (∆A ≈ h2). θpos/neg은 전선이 씨드로부터 퍼지는 방향(양/ 음)을 나타낸다. 즉, ξ는 아크 폭을 조절하는 파라미터로, 값이작 을수록 점프 방향성이 명확해지고, 너무 크게 설정하면 양쪽 플 럭스가 중첩되어 수평 성분이 상쇄된다. 본 논문에서는 이 값을 0.3으로 설정했다. 영역 A는 재결정 전선(Front)의 말단부 주변에 위치한 좁은 각도 구간으로, 증발 플럭스의 비대칭성이 가장 크 게 나타나는 영역을 의미한다. 파라미터 ξ는 이 아크 영역의 반각 (Angular half-width)을 나타내며, 적분 범위가 지나치게 넓어져 수평 성분이 상쇄되는 문제를 방지하기 위한 제어 변수로 사용된 다. Ji는 얼음 표면에서의 증발 플럭스를, Jw는 액체 표면에서의 증발 플럭스를 의미한다. 두 값의 차이 (Ji−Jw)는 self-jumping을 유도하는 핵심 비대칭 모멘텀으로, 실제 실험에서 관찰되는 재결 정–증기화–이탈(Recalescence–vaporization–detachment) 현상을 단순화하여 반영한 물리적 근거이다. ∆A는 각 입자에 대응하는 유효 표면 면적을 의미하며, 실제 구현에서는 입자 간격 h의 제 곱에 비례하도록 정의한다. 이는 국소 증발 플럭스를 2차원 입자 기반 모델에서 면적 기반의 물리량으로 변환하기 위한 스케일링 요소이다.
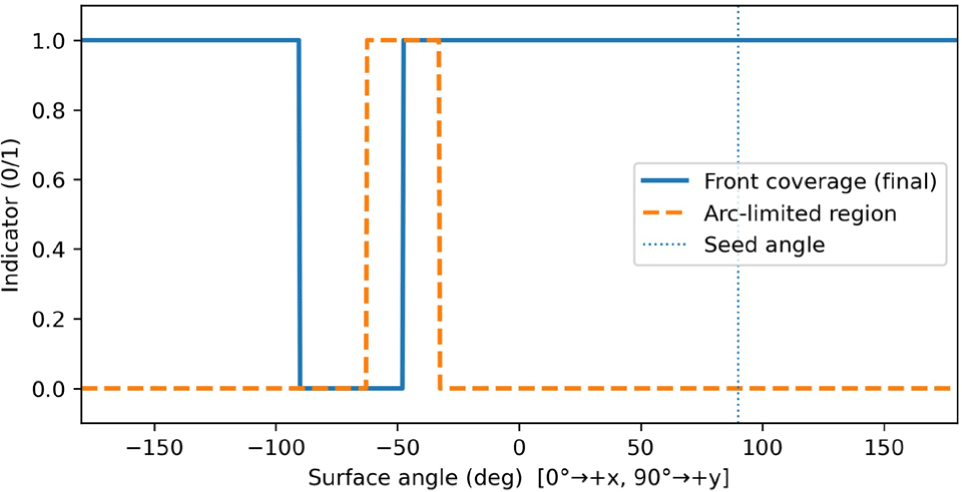
Figure 8은 재결정 전선(Front)이 퍼져나가는 각도 범위와 임펄 스 적분이 제한되는 아크(Arc) 영역의 관계를 나타낸다. 파란색 실선은 시뮬레이션의 최종 시점에서 전선이 도달한 범위를 의미 하며(Front coverage), 주황색 점선은 전선의 끝단 주변에 정의된 아크 제한 적분 영역을 나타낸다. 세로 점선은 핵생성이 발생한 각도 θseed를 표시한다. Figure 8에서 보이듯, 전선을 따라 형성된 전체 결빙 범위 중 아크 제한 영역은 전선의 말단부(θpos/neg)를 중심으로 폭(ξ)만큼 좁게 설정되어 있다. 이는 모든 표면 방향에 서 증발 플럭스를 동일하게 적분할 경우 서로 반대 방향의 수평 성분이 상쇄되어 결국 순수한 점프 방향성이 사라지는 문제를 방 지하기 위함이다. 따라서 아크 형태의 제한은 실제 물리 현상에서 관찰되는 비대칭적 증발 플럭스의 방향적 집중을 단순화해 표현 하며, 이후 임펄스 적분(∆J) 단계에서 점프 방향을 일관성 있게 결정하도록 한다. 본 논문에서는 gain 계수인 ζ를 추가하여 Jnet 를 계산한다 (see Equation 18). 본 논문에서는 ζ를 60으로 설정 했다.
다시 말해, Jnet 은 얼음 표면(Ji)과 액체 표면(Jw) 사이의 비 대칭적인 증발 플럭스 차이로부터 유도된 단위 면적당 순임펄스 밀도이며, self-jumping의 추진력 생성의 직접적인 원인이 된다. ζ는 그 물리적 스케일을 조절하는 보정 계수이다.
각 입자의 단위 면적당 임펄스는 Fi = niJnet ∆A로 계산된 다. 이후 전체 입자에 대해 선형 및 각(Angular) 임펄스를 각각 누적한다 (see Equation 19).
이러한 아크 기반 방향성 임펄스 적분 방식은 수평 성분이 제거 된 순수한 비대칭 플럭스 차이를 누적하여 실제 실험에서 관찰되 는 self-jumping 현상의 방향성과 유사한 결과를 생성한다. 특히, ξ와 ζ는 점프 강도와 각도에 직접적인 영향을 미치는 주요 제어 인자로서, 시뮬레이션에서 물리적 현상 재현뿐 아니라 그래픽스 응용 측면에서의 제작 제어성을 함께 확보할 수 있다. Jacc와 τacc 는 아크 영역에서 발생하는 플럭스 차이를 시간에 따라 적분하여 얻는 선형 및 각 임펄스이다. 이 두 값은 분리(Detachment) 단계 에서 최종 점프 힘과 회전 토크를 생성하는 원천이 된다.
Figure 9는 아크 제한 적분 영역 내에서의 방향성 임펄스 밀도 (Jnet)와 그 누적 성분(Cumulative projections)의 변화를 나타낸 다. 파란색 실선은 각 표면 각도에 대한 Jnet = ζ·(Ji − Jw)의 분포를, 주황색 파선과 초록색 점선은 각각 누적된 Jx와 Jy 성분 을 의미한다. 세로 점선은 핵생성 각도 θseed를 표시한다.

Figure 9에서 볼 수 있듯이, Jnet은 전선(Front)의 말단부에서만 높은 값을 가지며, 이 구간에서 Jy 성분이 비대칭적으로 누적된 다. 이는 아크 제한 적분이 전선의 상·하 방향 중 한쪽(예: y 방향) 에서 더 강한 플럭스 차이를 수집함을 의미한다. 결과적으로 Jx 성분은 양쪽 아크에서 거의 상쇄되어 0에 가까워지고, Jy 성분만 남아 점프 방향성을 결정하게 된다. 이러한 누적 결과는 곧 전체 임펄스 벡터 Jacc의 주된 방향이 수직 성분(즉, Seed 반대 방향) 으로 정렬된다는 것을 보여준다.
따라서 Figure 9는 아크 제한 적분이 단순한 공간 필터링이 아 니라, 수평 성분의 상쇄를 억제하고 self-jumping을 유도하는 비 대칭 임펄스의 물리적 축적 과정임을 정량적으로 설명한다.
임펄스의 누적이 완료되면, 일정 임계값(∥Jacc∥ > Jcrit)을 초 과하는 시점에서 실제 점프를 유발하는 힘(Force)이 생성된다. 이 힘은 누적된 임펄스의 시간 평균에 비례하여 다음과 같이 계산된 다 (see Equation 20).
여기서 ∆tJ 는 self-jumping 직전에 전선(Front) 주변에서 증발 플럭스 불균형이 누적되는 짧은 시간 구간이다. 즉, 재결정 전선 말단부에서 발생하는 증발 플럭스 불균형이 유지되는 짧은 시간 구간을 의미한다. 이는 실제 self-jumping 실험에서 관찰되는 밀 리초(ms) 단위의 짧은 반응 시간을 모델링하며, 최종 점프 힘을 계산할 때 사용되는 시간 평균 구간을 결정한다.
실제 물리적으로는 수 몇 밀리초(ms) 수준으로, 본 논문에서는 약 0.004s로 설정했다. 힘의 작용점은 전선(Front) 후면부의 중심 질량 근처(xcm)에 배치되며, 이 위치는 증발 플럭스가 가장 강 하게 비대칭으로 분포하는 영역에 해당한다. 결과적으로 Fjump 는 씨드 방향의 반대편(θseed)을 향해 작용하며, 이는 실험적으로 관찰된 점프 방향성과 일치한다.
힘의 크기 ∥Fjump∥은 누적된 임펄스 세기(∥Jacc∥)와 임펄스 창 길이(∆tJ), 그리고 플럭스 차이(Ji − Jw)의 평균값에 의해 결 정되며, 이는 실제 self-jumping에서 관찰되는 반비례적 반응— 즉, 짧은 시간에 강한 점프 혹은 긴 시간에 완만한 점프—를 자 연스럽게 재현한다. 이러한 힘은 rigid-body 단계에서 초기 속도 (v0 = Fjump/M )로 전달되어 결빙 방울이 실제로 이탈하는 동역 학적 거동을 유도한다. 따라서 본 연구의 전체 파이프라인은 “증 발 플럭스 불균형→방향성 임펄스 누적→힘 생성→자발적 이탈 (jump)”로 이어지는 완결된 self-jumping 동역학 과정을 시각적 으로 모델링한다.
Figure 10은 단위 원 상에서 아크 제한 적분이 수행되는 영역과, 이를 통해 얻어진 누적 임펄스 벡터 Jacc 및 점프 힘 벡터 Fjump 의 공간적 관계를 나타낸다. 원 둘레는 물방울의 표면을 단순화 한 것으로, 파란색과 주황색 점은 각각 전선(Front)의 양과 음의 방향에서 선택된 아크 적분 영역을 의미한다.
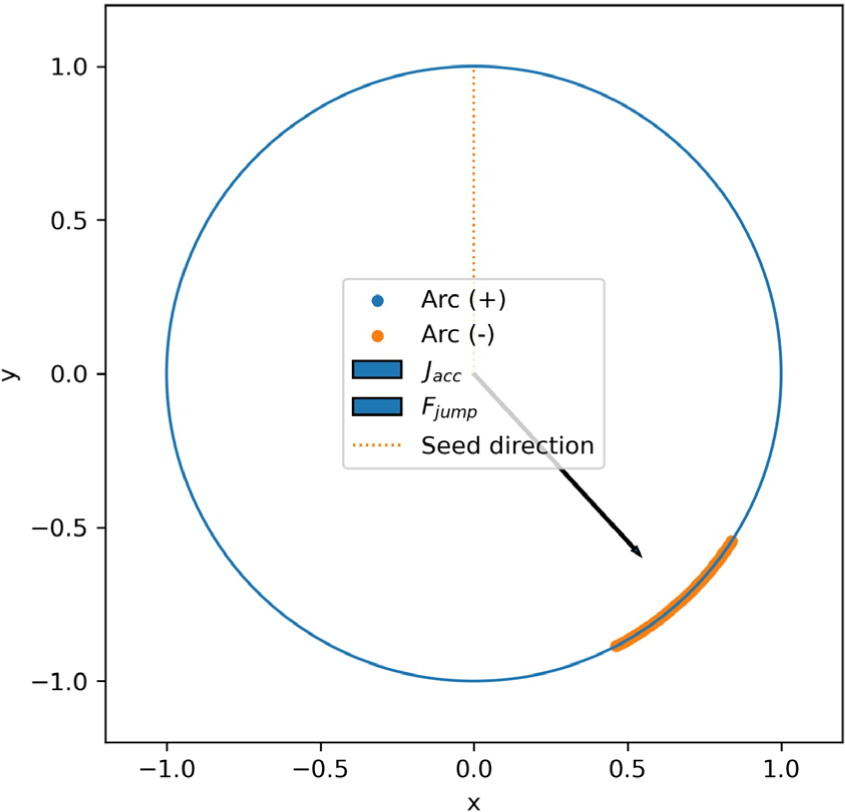
Figure 10의 중심에서 시작하는 두 화살표는 임펄스의 누적 결 과를 벡터 형태로 표현한 것으로, 짙은색 화살표는 누적된 임펄스 Jacc, 옅은색 화살표는 점프 시 발생하는 힘 Fjump를 나타낸다. 이 벡터들은 전선 후면부에서 비대칭적으로 발생하는 증발 플럭 스 차이에 의해 생성되며, 결과적으로 씨드 방향의 반대편(θseed) 으로 향한다. 이는 실제 실험에서 관찰되는 self-jumping의 방향 성과 일치한다.
따라서 Figure 10은 아크 기반 적분 과정이 공간적으로 비대 칭적인 플럭스 차이를 효과적으로 누적하여 결국 Droplet 전체가 반작용(Force)을 받아 이탈하는 자발적 점프 동역학의 기하학적 구조를 시각적으로 보여준다.
5 솔버 확장: 이미지 마스크를 이용한 임의 형상 처리
이번 장에서는 원 형태의 가정에서 벗어나, 사용자가 제공하는 마스크 이미지를 입력으로 받아 임의 실루엣의 얼음 형상을 다 루는 확장 솔버를 소개한다. 핵심 아이디어는 세 가지로 요약된 다. 첫째, 마스크를 바탕으로 입자를 배치하는 초기화 단계, 둘째, 형상에 종속되지 않도록 표면과 외측 법선을 견고하게 추정하 는 단계, 셋째, 전선(Front)의 각도 기반 파라미터화를 경계-따라 (Geodesic-like) 파라미터화로 치환하는 단계이다. 이 외에 열 전 달, 상변화, 방향성 임펄스 누적 등 핵심 모델은 기존 프레임워크 와 동일하게 유지된다.
마스크 이미지는 흑백(또는 그레이스케일)로 해석하며, 밝은 영 역을 유효 도메인으로 간주해 그 내부에만 입자를 배치한다. 입자 배치는 두 방식을 제공한다. (1) 격자 샘플과 마스크 필터는 구현 이 간단하고 빠르며, (2) Poisson-disk 샘플링은 보다 자연스러운 분포를 제공해 비균일 밀도에서도 표면 검출이 안정적이다. 배치 가 끝나면 시뮬레이션 좌표계의 기준점을 다음과 같이 정의한다 (see Equation 21).
이는 물리적 의미의 무게중심과 정확히 일치할 필요는 없지만, 미리보기와 후속 연산(표면 판정, 법선 추정, 전선 전파 등)의 기 준 프레임으로 충분히 일관된 역할을 수행한다.
원 형태 가정에서는 씨드 각도 θseed를 기준으로 양과 음 방향의 전파 각도 θpos/neg(t) = ∫ vpos/neg dt를 사용하여 전선의 진행을 단순한 각도 공간에서 기술하였다. 그러나 임의 형상에서는 이러 한 각도 기반 표현이 더 이상 유효하지 않으므로, 본 연구에서는 이를 경계를 따라 전개되는 호 길이 기반 파라미터화로 확장한다.
먼저 표면 입자들로만 구성된 그래프 G = (Vs, E)를 정의하 고, 간선 가중치는 인접한 표면 입자 간의 거리로 설정한다. 씨 드 입자가 결정되면, Dijkstra 또는 BFS 알고리즘을 이용하여 각 표면 입자 i에 대해 씨드로부터의 서명된 경계 거리 si를 계산 한다. 이때 부호는 씨드 부근의 접선 벡터 방향으로 양과 음을 구분한다.
시간 t에 따른 전선의 진행 위치는 다음과 같이 정의된다 (see Equation 22).
여기서 vpos/neg는 전선이 양과 음 방향으로 전파되는 속도이다.
입자 i가 전선 내부에 포함되는 조건은 다음과 같이 정의된다 (see Equation 23).
즉, 씨드로부터 일정 거리 이내의 경계 입자들이 시간에 따라 순차적으로 전선 내부로 편입되며, 이는 원 형태의 경우 s ∝ θ로 귀결되어 기존 모델의 특수한 형태로 수렴한다. 이와 같은 경계 기반 매개변수화는 복잡한 형상에서도 전선의 확산 방향과 속도 를 부드럽게 추적할 수 있도록 하며, 결빙 경계의 불연속적 확산 문제를 효과적으로 방지한다.
임펄스 적분 단계에서는 수평 성분의 상쇄를 줄이기 위해, 전선의 끝단 영역에 해당하는 얇은 아크 구간만을 선택적으로 적분한다. 이 접근은 물리적으로 전선 말단에서 증발 플럭스의 불균형이 가장 크게 발생한다는 관찰에 기반하며, 불필요한 반대 방향의 기여를 효과적으로 제거한다.
원 형태에서는 아크 폭이 각도 범위로 정의되었으나, 임의 형 상에서는 각도대신 경계를 따라 측정된 호 길이 폭 warc를 사용 한다. 즉, 아크 적분 영역 A는 다음과 같이 정의된다 (see Equation 24).
여기서 si는 씨드로부터의 서명된 경계 거리이며, spos/neg(t)는 시간 t에서 전선이 양/음 방향으로 진행한 호 길이이다.
이 아크 영역 내에서의 방향성 임펄스는 다음과 같이 계산된다 (see Equation 25).
여기서 Ji는 얼음 표면의 증발 플럭스, Jw는 액체 표면의 증발 플 럭스이며, ni는 해당 입자의 외측 법선 벡터이다. 여기서 Jnet은 앞서 Equation 18에서 정의한 순임펄스 밀도와 동일하다.
선형 임펄스와 각(Angular) 임펄스는 시간에 따라 누적되며, 그 식은 다음과 같다 (see Equation 26).
임펄스가 임계치에 도달하면, 누적된 임펄스로부터 점프 힘과 토크가 계산된다 (see Equation 27).
이 계산 절차는 기본적으로 원 형태의 모델과 동일하지만, 아 크 정의가 각도 공간 대신 호 길이 공간으로 바뀌었다는 점에서 차이가 있다. 결과적으로 점프의 방향은 여전히 씨드 반대측으로 형성되며 (이는 실험적 관찰과 일치함), 크기는 ∥Ji − Jw∥의 아크 내 평균값과 시간 창 ∆tJ 에 의해 제어된다. 즉, 임의 형상에서도 본 모델은 비대칭 플럭스에 의한 실제 self-jumping의 방향성과 동역학적 특성을 일관성 있게 재현한다.
핵생성은 표면 온도 Ti가 임계 과냉각 Tnuc = Tm − ∆Tnuc에 가장 먼저 도달하는 위치에서 자동으로 결정된다. 재결정 밴드에서는 Mushy 클램프를 적용하여 Ti ∈ [Tm − wm, Tm + wm] 범위를 유 지하고, 액상비는 다음과 같이 점진적으로 감소시켜 고상(Solid) 으로의 전이를 표현한다 (see Equation 28).
결과적으로 형상이 복잡해져도 열전달과 상변화의 핵심 절차 는 기존 프레임워크와 동일하게 유지되므로, 파이프라인의 구현 복잡도는 크게 증가하지 않는다.
이미지 기반 샘플링에서는 입자 간격이 균일하지 않을 수 있 다. 최근접 거리의 중앙값 dnn,med를 이용해 이웃 반경을 h ≈ 2.5 dnn,med로 자동 추정하면 표면 판정이 안정적이다. 법선은 중 심 C 방사 방향 대신 밀도 기울기로 추정한 외측 법선을 사용하는 편이 임의 형상 경계에서 더 견고하다. 또한 전선 파라미터화는 각도 대신 경계-따라 정의한 호 길이를 사용한다. 표면 그래프에 대한 Dijkstra/BFS의 시간 복잡도는 O(M log M) 수준으로 충분 히 빠르며, 전선 위치는 프레임마다 증분적으로 업데이트할 수 있다. 아크 폭 warc(원판 모델의 ξ에 대응하는 길이 파라미터)는 너무 크면 수평 성분 상쇄가 커지고, 너무 작으면 노이즈에 민감 해지므로 장면별로 적정 범위를 선택하는 것이 바람직하다.
제안된 확장 솔버는 각도 기반 절차를 경계-따라(Geodesic-like) 파라미터화로 치환하고, 밀도기반 표면/법선과 호 길이 아크 적분을 도입함으로써 임의 실루엣에서도 물리적 일관성과 제작 제어성을 동시에 확보한다. 원판 모델의 대부분의 수식은 그대로 유지되며, 전선 전파와 임펄스 적분의 “좌표계”만 바뀐다고 이해 할 수 있다.
6 실험 결과
본 절에서는 제안한 재결정 기반 입자 시뮬레이션 프레임워크의 시각적 결과와 물리적 타당성을 검증한다. 우선 단일 원형 형상 을 대상으로 자동 핵생성, 재결정 전선의 전파, 그리고 아크 제한 임펄스 적분 과정을 순차적으로 시각화하여 제안 알고리즘의 내 부 동작을 분석하였다. 이후에는 사용자가 임의로 씨드 위치를 지정한 경우, 형상 기하에 따른 Self-jumping 거동의 차이, 그리 고 샘플링 방식(Poisson-disk vs. grid sampling)에 따른 강건성을 비교함으로써 제안 기법의 일반성과 제어성을 함께 검증하였다. 이러한 일련의 실험은 제안된 모델이 물리적 일관성, 형상 독립 성, 사용자 제어성을 모두 충족함을 보여준다.
Figure 11은 제안 기법의 핵심 단계를 시각적으로 요약한다. Figure 11a는 초기 입자 분포로, 중심 C와 반지름 R을 갖는 원판 영역에 균일 간격으로 배치된 파티클들의 위치를 보여준다. 이 상태에서 모든 입자는 액체 상태로 시작하며(αi = 1), 이웃 반경 h에 기초한 커널 수밀도 평가를 통해 표면 여부를 판정할 준비를 마친다.
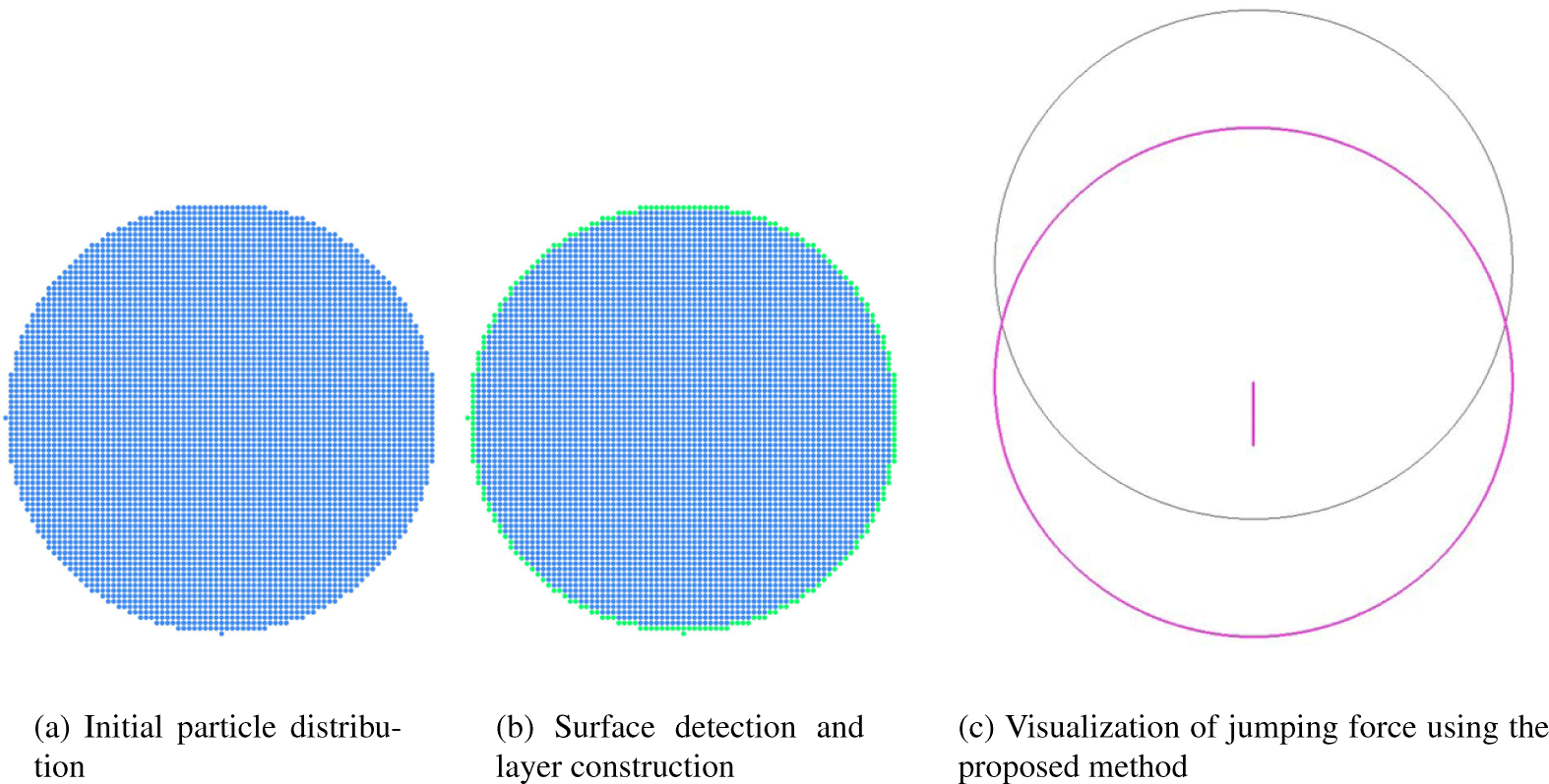
Figure 11b는 표면 탐지와 레이어 구축 결과로, 커널 수밀도가 낮은 입자를 표면으로 분류하고 BFS를 통해 표면으로부터 내부 로 확장하는 레이어 인덱스를 부여한 장면이다. 바깥쪽의 녹색 점들은 레벨 0(표면층)에 해당하며, 이는 이후 재결정 전선이 표 면을 따라 진행될 때 껍질 커버리지와 내부 전파 판정의 기준으로 사용된다.
Figure 11c는 제안한 아크 제한 방향성 임펄스 적분을 통해 산출된 점프 힘(Jumping force)의 시각화 결과다. 회색 윤곽선은 초기 얼음의 위치(레퍼런스)이며, 보라색 화살표는 누적 임펄스 Jacc를 시간창 ∆tJ 로 나누어 얻은 점프 힘 Fjump = Jacc/∆tJ 의 방향과 상대 크기를 나타낸다. 보라색 윤곽선은 점프 이후 rigid-body 이동이 적용된 얼음 형상의 새로운 위치를 나타내며, 이는 초기 실루엣이 형태 변형 없이 공간적으로 이동했음을 의미한다. 씨드 각 θseed의 반대편(실험 보고와 일치하는 방향)으로 이탈하 는 경향이 명확히 드러난다. 이는 전선 말단부의 얇은 아크 주변 에서만 증발 플럭스 차 Ji − Jw 를 적분함으로써, 서로 상쇄되기 쉬운 수평 성분을 억제하고 점프 방향성을 안정적으로 보존한다 는 본 방법의 핵심 아이디어를 뒷받침한다.
Figure 12는 초기 핵생성(Seed) 위치를 본 논문에서 제안한 물 리 기반 방식(임계 과냉각에 따른 자동 판정)이 아닌, 사용자가 임의로 지정했을 때의 self-jumping 결과를 보여준다. 세 실험은 각각 서로 다른 초기 씨드 위치에서 시작되었으며, 결과적으로 점프 방향과 이동 경로가 그에 따라 달라지는 양상을 나타낸다. 이는 제안된 물리 기반 모델이 실제 열과 증발 플럭스 분포에 따 라 자동으로 Seed를 결정하는 것과 달리, 사용자가 Seed 위치를 수동으로 지정함으로써 결빙 방향과 점프 벡터를 직접 제어할 수 있음을 시사한다. 즉, 본 알고리즘은 물리적 타당성을 유지하면 서도 아티스틱 제어나 상호작용적인 시뮬레이션 환경에도 확장 가능함을 보여준다. 결과적으로, 이러한 사용자 제어 실험은 본 방법이 단순한 물리 모델에 그치지 않고, 시각적 연출 및 인터랙 티브 콘텐츠 제작에도 활용 가능한 유연한 프레임워크임을 입증 한다.
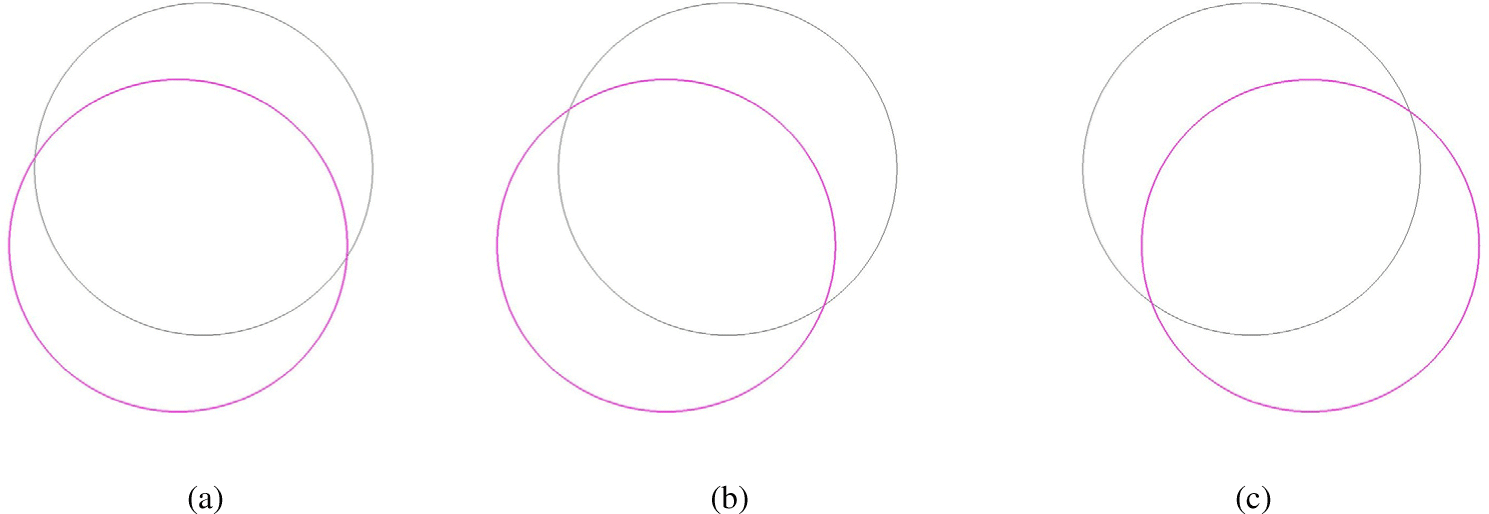
Figure 13은 제안된 확장 솔버가 단순한 원형이 아닌 임의의 실루엣 형상 (Mask-based geometry)에 대해서도 안정적으로 동 작함을 보여준다. 각 열은 입력 마스크 이미지(검은 배경의 흰색 형상)와 해당 형태 내에 균일하게 배치된 초기 입자 분포(회색 점) 를 나타낸다. 하늘색으로 표시된 입자들은 self-jumping 단계에서 임펄스가 작용한 이후 이동한 위치를 의미하며, 이는 제안된 아 크 제한 임펄스 적분 알고리즘이 복잡한 경계에서도 물리적으로 일관된 방향성 (Force vector)을 유지함을 시각적으로 보여준다.
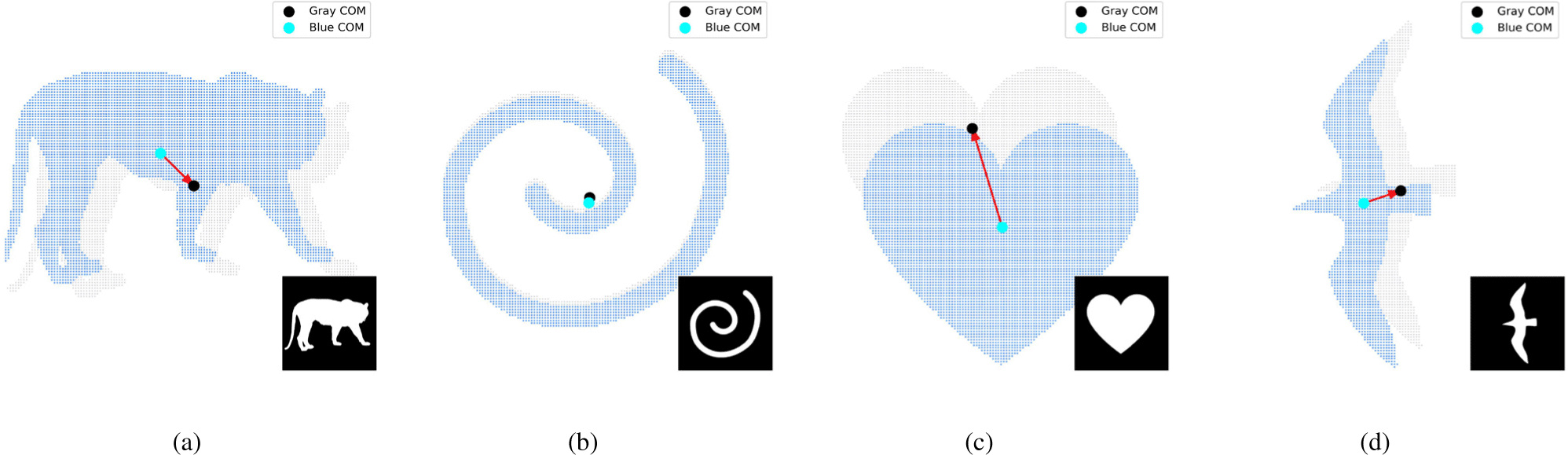
모든 경우에서 전선(Front) 전파와 임펄스 누적은 경계를 따라 자연스럽게 확산되었으며, 형상이 비대칭이거나 굴곡이 심한 영 역에서도 안정적인 점프 방향성을 유지하였다. 이는 기존의 원판 모델과 달리, 본 논문에서는 경계-따라(Geodesic-like) 파라미터 화가 형상의 복잡도에 독립적으로 적용될 수 있음을 입증한다. 또한, 실루엣별로 전선의 진행 경로가 달라지더라도 점프의 중심 방향이 핵생성 씨드의 반대편으로 향하는 물리적 일관성이 관찰 되었다.
Figure 13은 임의의 실루엣 형상에 따라 Self-jumping의 방향 성과 크기가 다르게 나타나는 현상을 보여준다. 이는 각 형상의 경계 곡률, 면적 비대칭, 그리고 씨드 위치에 따른 전선 진행 경 로가 서로 다르기 때문이다. 예를 들어, 곡선이 안쪽으로 말린 나 선형에서는 전선이 한쪽으로 집중되어 불균형한 아크 적분이 발 생하며, 상대적으로 큰 순임펄스(Jnet)가 형성되어 강한 점프를 유도한다. 반면, 대칭적인 하트나 새 형태에서는 플럭스가 양측 으로 분산되어 점프 크기가 작고 중심 방향으로 수렴하는 경향이 나타난다.
이 결과는 제안된 알고리즘이 형상 복잡도나 비대칭성에 민감 하게 반응하며, 이를 통해 실제 물리적 플럭스 불균형을 반영한 자연스러운 점프 동역학을 재현함을 의미한다. 즉, 단순한 원판 형태를 넘어, 형상의 기하학적 특성에 따라 임펄스의 방향성과 크기가 달라지는 현상이 본 시뮬레이션에서도 일관되게 재현되 었다.
Figure 14는 동일한 실루엣 형상에 대해, Poisson-disk 샘플링을 사용하여 초기 입자 분포를 구성했을 때의 Self-jumping 결과를 보여준다. 회색 점은 초기 입자의 위치를, 하늘색 점은 임펄스가 작용한 후 이동한 위치를 나타낸다. 전반적으로 점프 방향과 크 기는 이전 격자 기반 결과와 유사하지만, 세부적으로는 약간의 차이를 보인다. 이러한 차이는 입자 분포의 공간적 불균일성에서 기인한다. Poisson-disk 샘플링은 인접 입자 간 최소 거리 rmin을 보장하여 자연스럽고 랜덤한 분포를 형성하지만, 국소적으로는 입자 간 간격이 일정하지 않기 때문에 커널 밀도 추정 및 표면 법선 계산 시 작은 플럭스 편차(Flux deviation) 가 발생한다. 결과 적으로, 임펄스 적분 시 지역적 불균형이 반영되어 약간의 비대칭 점프가 나타날 수 있다.
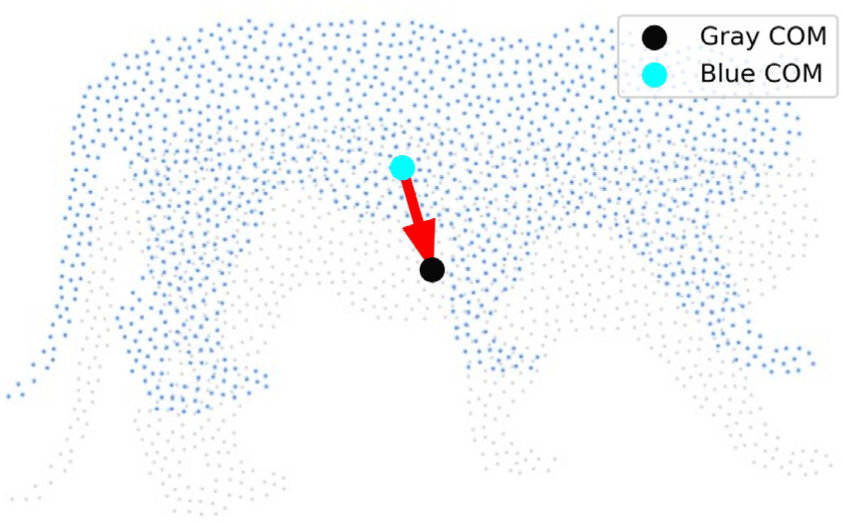
그러나 이러한 미세한 차이에도 불구하고, 전체적인 점프 방 향은 여전히 핵생성 각의 반대편으로 일관되게 유지되며, 이는 제안된 알고리즘이 입자 배치 방식에 강건하게 설계되었음을 의 미한다. 즉, 본 모델은 격자 샘플링이나 포아송 샘플링 등 다양한 분포 방식에서도 물리적 일관성과 시각적 안정성을 유지한다는 점에서 실용적이다.
본 연구는 재결정 기반 self-jumping 현상의 핵심 메커니즘을 검증하기 위해 대표적인 냉각 조건과 단일 초기 핵생성 사례를 중심으로 실험을 구성하였다. 다만, 다양한 온도 구배나 초기 결 정(seed) 구성, 외부 열환경 변화와 같은 조건을 체계적으로 변 화시키며 시각적 결과를 비교하는 실험은 제안된 모델의 물리적 타당성과 일반성을 더욱 강화할 수 있는 중요한 확장 방향이다. 이러한 다중 조건 비교는 재결정 전선의 비대칭성 변화, 임펄스 누적 패턴의 이동, 점프 방향성의 변형 등을 정량적으로 분석하 는 데에도 의미가 있으며, 향후 연구에서 단계적으로 포함할 계 획이다.
또한, 본 프레임워크는 2D 입자 기반 접근을 바탕으로 구성되 었지만, 전선 전파, 경계 기반 아크 적분, 열–상변화 모델은 모 두 3차원 공간으로 자연스럽게 확장 가능한 구조를 갖는다. 따 라서 향후에는 3D 볼륨 입자 또는 점군 기반 시뮬레이션으로 재 결정–증발–점프 과정을 통합하여 보다 현실적이고 응용 범위가 넓은 self-jumping 동역학 모델로 발전시킬 예정이다.
본 연구의 시뮬레이션 실험은 NVIDIA RTX 4090 GPU(24GB VRAM)와 Intel Core i9-13900K CPU, 64GB 메모리로 구성된 워 크스테이션 환경에서 수행되었다. 파티클 기반 계산 및 임펄스 적 분은 Python 3.1 환경에서 PyCUDA 기반 CUDA 커널로 구현되었 으며, 시각화 및 후처리는 NumPy·Matplotlib·OpenCV를 활용 하였다. 이러한 HW/SW 사양은 제안된 프레임워크의 계산 비용 과 실시간 적용 가능성을 평가하는 기준이 되며, 동일한 파라미터 조건을 유지할 경우 실험을 동일하게 재현할 수 있음을 의미한다.
7 결론 및 향후 연구
본 연구에서는 결빙 과정에서 발생하는 재결정(Recalescence)과 증기화 모멘텀(Evaporative momentum)을 단순화된 물리 모델로 통합하여, 자기 점프(Self-jumping) 현상을 시각적으로 재현하는 입자 기반 시뮬레이션 프레임워크를 제안하였다. 제안 기법은 (1) 표면 온도 분포를 이용한 자동 핵생성(Auto-nucleation), (2) 재결정 전선의 양방향 전파(Front propagation), (3) Mushy band 기반 열 안정화(Thermal clamp), (4) 아크 제한 방향성 임펄스 적분(Arc-limited impulse integration), (5) 강체 전환(Rigid-body transition) 단계를 일관된 파이프라인으로 연결함으로써, 복잡한 열–유체 방정식을 해석하지 않고도 물리적으로 타당한 점프 방 향성과 크기를 효율적으로 생성할 수 있음을 보였다.
또한, 이미지 마스크 기반 확장 솔버를 통해 원형뿐 아니라 임 의의 실루엣에서도 일관된 Self-jumping 거동을 재현하였으며, 비대칭 형상에서는 플럭스 집중으로 인한 강한 점프, 대칭 형상 에서는 균형 잡힌 약한 점프를 관찰할 수 있었다. 이는 제안된 방법이 형상 특성에 따른 모멘텀 불균형(Momentum imbalance) 을 자연스럽게 반영함을 시사한다.
향후 연구에서는 다음 세 가지 방향으로 확장을 고려할 수 있 다.
-
3차원 확장: 현재의 2D 입자 기반 모델을 3D 볼륨 입자 혹 은 점군 기반 시뮬레이션으로 확장하여 실제 실험과 유사한 공간적 점프 거동을 재현할 필요가 있다.
-
열–유체 결합 모델링: 단순화된 증발 모멘텀 근사를 넘어, 열전달 방정식과 증기 플럭스의 상호작용을 포함하는 다중 물리 기반 시뮬레이션으로 발전시킬 수 있다.
-
실시간 시각화 및 인터랙티브 응용: GPU 병렬화를 통해 시 뮬레이션 속도를 향상시키고, VR/AR 환경이나 인터랙티브 아트 콘텐츠 제작에도 활용할 수 있는 실시간 버전으로 확장 할 수 있다.
결론적으로, 본 연구는 재결정에 의해 유도되는 자발적 점프 현 상을 시각적으로 모델링한 최초의 그래픽스 접근으로서, 물리적 사실성과 예술적 표현 가능성을 동시에 갖춘 효율적 시각 시뮬레 이션 프레임워크를 제시하였다.

