메시 기반 GPU 마칭큐브

김, 현준; 김, 도훈; 김, 민호

doi:10.15701/kcgs.2018.24.1.1

J Korea Comput Graph Soc 2018; 24(1):1-8

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2018.24.1.1

Article

메시 기반 GPU 마칭큐브

김현준, 김도훈, 김민호^*

Mesh-based Marching Cubes on the GPU

Kim Hyunjun, Kim Dohoon, Kim Minho^*

Author Information & Copyright ▼

서울시립대학교 컴퓨터과학과

Department of Computer Science and Engineering, University of Seoul

^*corresponding author: Minho Kim/University of Seoul(minhokim@uos.ac.kr)

© Copyright 2018 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 20, 2017 ; Revised: Sep 04, 2017 ; Accepted: Feb 07, 2018

Published Online: Mar 01, 2018

요 약

본 논문에서는 삼각형 집합(triangle soup)형식의 등가면(isosurface)을 추출하는 기존의 마칭큐브 기법을 개선하여, 연결된 메시(connected mesh)형식으로 추출하는 실시간 기법을 제안한다. 이를 통해 기존에는 불가능했던 다양한 렌더링 기법을 사용하여 동적으로 변하는 등가면을 렌더링할 수 있고, 등가면의 위상(topology)과 기하(geometry) 정보 등을 추출할 수 있다. 또한 지오메트리 셰이더 (geometry shader) 에서 사용하는 인접 삼각형 형태의 구조 (GL_TRIANGLES_ADJACENCY) 를 생성하여 보다 다양한 셰이딩 기법을 지원한다. 본 기법은 기존 마칭큐브에 삼각형들을 연결하는 후처리 과정을 추가한 기법에 비해 300% 정도의 향상된 등가면 추출 속도를 보인다.

Abstract

We propose a modified real-time marching cubes technique that extracts isosurfaces in the form of connected meshes instead of triangle soup. In this way, a various mesh-based isosurface rendering techniques can be implemented and additional information of the isosurfaces such as its topology can be extracted in real-time. In addition, we propose a real-time technique to extract adjacency-triangle structure for geometry shaders that can be used for various shading effects such as silhouette rendering. Compared with the previous technique that welds the output triangles of classical marching cubes, our technique shows up to 300% performance improvement.

Keywords: 등가면; 메시; GPGPU; 마칭큐브

Keywords: isosurface; mesh; GPGPU; marching cubes

1 서론

마칭큐브 (marching cubes) 기법[1] 은 볼륨 데이터 (volume dataset) 로부터 등가면을 추출하는 가장 고전적이고 보편적인 기법으로, 이후 GPU(Graphics Processing Unit) 를 통한 병 렬 연산을 활용한 여러 기법이 제안되었다. 하지만 마칭큐브의 결과물은 서로 연결되지 않은 삼각형들의 집합 (triangle soup) 으로 이루어져 있어서 중복된 정점들의 개수가 매우 많고, 메시의 연결 정보가 필요한 일부 고급 렌더링 기법에서 사용하기 힘든 단점이 있다. 이를 개선하기 위해 같은 좌표에 위치한 정점들을 하나로 합쳐서 인접한 삼각형들을 연결하는 후처리 과정 (vertex welding) 을 추가할 수 있으나[2, 3], 이는 추출되는 메시를 구성하는 정점의 개수에 따라 성능이 크게 좌우된다는 단점이 있다 (그림 6 참고). 본 논문은 기존의 마칭큐브 기법을 개선하여 별도의 후처리 과정 없이 삼각형들이 실제로 연결되어 있는 삼각형 메쉬 (triangle mesh) 형태의 등가면을 추출하는 기법을 제안한다.

2 관련 연구

Lorensen[1] 이 제안한 마칭큐브 알고리즘은 의료데이터의 시각화가 주된 목적이다. 이후 오랜 기간 동안 마칭큐브알고리즘은 여러 방향으로 성능이 개선되었는데, 다수의 기법들은 볼륨 데이터의 기하구조를 분석하여 등가면이 지나는 셀을 샘플링하여 불필요한 연산을 줄이는 방법을 사용하였다[4, 5, 6]. 하지만 최근에는 그래픽스 하드웨어의 발달에 따라 고성능의 GPU 연산을 사용할 수 있게 되어 복잡한 기하적인 특성들을 분석하지 않고도 빠르게 연산이 가능하여 실시간 렌더링에 활용하는 것이 가능해졌다[7, 8]. 이러한 GPU기반의 마칭큐브에서 고려되어야 할 요소 중 하나는 버퍼에 병렬로 데이터를 추가할 때 생기는 동시 접근 문제를 해결하는 것으로, 가장 쉬운 방법은 CUDA SDK 에 포함된 GPU 기반의 마칭큐브와 같이 구간 합 (prefix sum) 을 사용하는 것이다. 이 방법은 잘 알려진 GPU 기반의 구간 합[9] 을 사용할 수 있어서 구현이 쉽고 우수한 성능을 보인다. 또 다른 방법은 히스토피라미드 (histopyramid) 구조를 사용한 방법으로 Dyken[10]에 의해 제안된 방법이다. 이 방법은 리덕션 (reduction) 기반의 탐색구조를 사용함으로써 전체 데이터에 대한 구간 합을 계산하는 것보다 빠른 성능을 보였다.

GPU기반의 마칭큐브를 다른 응용 어플리케이션에 활용한 몇 가지 사례를 소개하면, Geiss는 2007년에 복잡한 지형렌더링 알고리즘에 GPU기반의 마칭큐브[11] 를 적용하였다. 하지만 이 방법은 그래픽스 파이프라인을 기반으로 설계되어 GPGPU 에 비해 복잡하고 다루기가 힘든 단점이 있다. Griffin[3] 은 등 가면의 곡률을 실시간으로 표현하기 위해, 마칭큐브로 추출된 메시에 후처리 과정으로 정점을 공유하는 삼각형의 정보를 생 성하였다. 이 방법은 후처리과정이 마칭큐브로부터 추출되는 정점의 개수에 많은 영향을 받는 단점이 있다. 최근 연구 결과로 Chen[8] 은 등가면 추출과 메시 최적화에 GPU기반의 마칭큐브를 사용하였다. 본 논문의 방법은 연결된 메시를 추출하는 과정이 Chen의 방법[8] 과 유사하지만, 지오메트리 셰이더에서 사용하는 GL_TRIANGLE_ADJACENCY 구조의 메시로 확장하는 과정을 추가하여 보다 다양한 렌더링 응용에 활용할 수 있도록 하였다.

3 이론적 배경

이 절에서는 등가면 추출 기법과 GPU기반의 알고리즘에 대해 간략히 소개한다.

3.1 등가면 추출 기법

등가면은 n차원 공간을 정의역으로 하는 연속함수 (contiuous function)의 레벨 집합(level set)으로, 특정 레벨의 등가면을 계산하거나 근사하는 것을 등가면 추출(isosurface extraction)이라 한다. 이 때 연속함수는 일반적으로 정수 또는 실수를 치역으로 하는 스칼라장 (scalar field) 의 형태를 가진다. 그래픽스 분야에서 등가면 추출은 CT(computer tomography)나 MRI(magnetic resonance imaging)같은 의료데이터와 SPH(smoothed-particle hydrodynamics) 와 같은 유체시뮬레이션 (fluid simulation) 등 볼륨 데이터 (volume data) 의 시각화 (visualization) 에 널리 활 용되고 있으며, 이러한 어플리케이션은 대부분 샘플링된 데이터인 유한스칼라장 (discrete scalar field) 로부터 등가면을 근사한 다.

등가면을 시각화하는 방법은 광선 투사법 (ray casting) 과 같은 볼륨 렌더링 (volume rendering) 과, 마칭큐브와 같은 곡면복구 기법 (surface reconstruction) 으로 나눌 수 있다[12]. 곡면복구 기법은 볼륨 렌더링에 비해 상대적으로 낮은 품질의 결과물을 생성하지만, 대체로 계산이 용이하고 결과물을 다루기가 쉬워 후처리 과정을 통해 다양한 기법들로 응용할 수 있는 장점이 있다.

이러한 곡면복구기법에 의해 추출되는 데이터는 주로 삼각형 메시 형태로 표현되는데 데이터 구조에 따라 각각의 삼각형들이 정점을 공유하는 형태의 삼각형 메시와 중복된 정점을 가지는 삼각형 집합 (triangle soup) 으로 구분할 수 있다. 일반적으로 삼각형 집합은 다루기가 편하고 생성이 간단하여 널리 사용되고 있지만, 각 정점들이 중복되어 있어 데이터의 크기가 상대적으로 크고 삼각형 간의 연결정보를 파악하기 어려운 단점이 있다. 이러한 단점으로 인해 삼각형 집합은 곡률 (curvature) 과 같은 기하 정보를 사용하는 렌더링기법에서 사용할 때에 매우 비효율적이다. 반면, 삼각형 메시는 생성과정이 복잡하지만 데이터의 크기가 상대적으로 작고 등가면의 기하정보가 남아있는 장점이 있기 때문에 다양한 응용 렌더링 기법에서 활용될 수 있다.

3.2 GPU기반 알고리즘

그래픽스 하드웨어가 발전하면서 GPU는 렌더링뿐만 아니라 범용 계산에도 활용되고 있다. GPGPU의 개념이 퍼지면서 다양한 분야에서 고성능 GPU를 쉽게 활용하게 되었고 많은 성능 향상 이 이루어졌다. 이러한 GPGPU는 기존의 싱글 쓰레드 (single thread) 기반의 알고리즘을 그대로 사용할 경우에는 대부분 비효율적이며, GPU 특성에 맞게 알고리즘의 수정이 필요하다.

GPGPU에서 흔히 발생하는 문제 중 하나는 동일한 버퍼 값을 병렬로 저장하는 것으로 동기화에 따른 성능저하를 최소화 하도록 해야 한다. 마칭큐브 과정에서는 각 정점이 정점 버퍼(vertex buffer) 에 저장할 때 동기화를 고려해야 하는데, 이를 해결하기 위한 방법은 크게 두가지로 나눌 수 있다. 첫 번째는 구간 합을 이용하여 구현한 방법이다. 구간 합은 수열의 누적 합을 각 항에 대하여 계산하는 것으로 Blelloch에 의해 병렬 처리가 연구되었으며[13], 이후 Harris에 의해 GPU에 최적화 되었다[9]. 구간 합을 사용하여 구현한 마칭큐브는 등가면 추출과정에서 생성될 수 있는 모든 정점을 표현하는 버퍼를 생성한다. 그리고 구간 합을 사용하여 실제로 생성되는 정점들에 대해 순차적인 값을 부여하고, 이 값을 통해 정점버퍼의 개별적인 위치에 추출된 정점을 저장한다. 두 번째는 정점 버퍼를 만들때 각 위치에 들어갈 정점 데이터를 검색하여 결정하는 방법으로 리덕션 기반의 탐색 알고리즘으로 구현이 가능하다[10]. 대부분의 경우 마칭 큐브를 통해 생성되는 정점의 개수는 전체 볼륨의 크기에 비해 매우 희소하기 때문에 구간 합에 비해 상대적으로 빠른 리덕션 기반의 탐색 알고리즘이 성능상의 이점이 많은 것으로 알려져 있으나[10], 상대적으로 구현이 복잡한 단점이 있다. 본 논문의 방법은 상대적으로 구현이 용이한 구간 합을 사용하였다.

4 메시 기반 마칭큐브

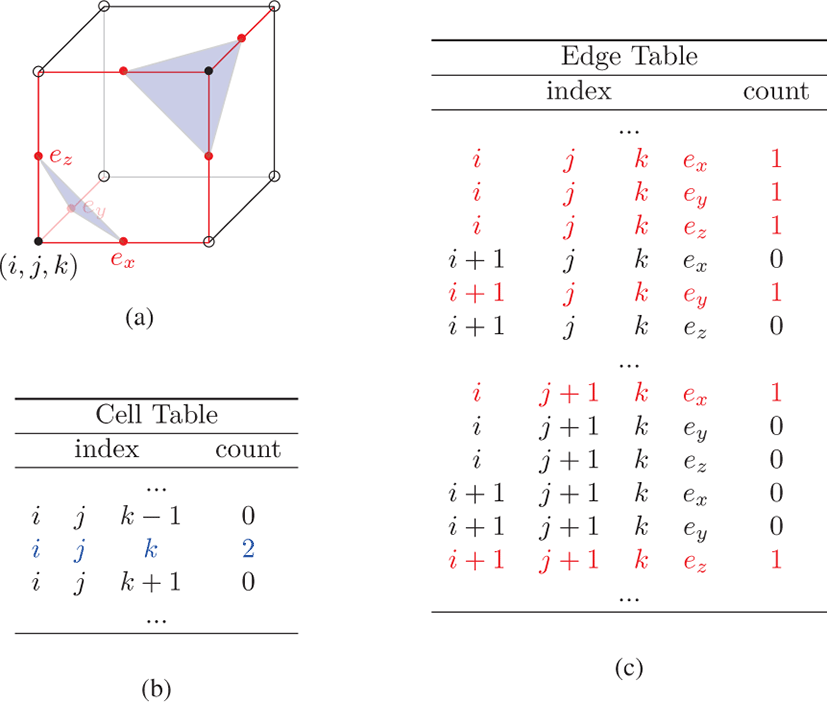
본 논문의 방법을 소개하기에 앞서 이 절에서 사용한 용어들을 정의한다. 복셀(voxel)은 3차원 공간의 정규 격자(regular grid) 상의 값을 표현하는 것으로, 볼륨 데이터의 기본 단위 요소이 다. 셀 (cell) 은 복셀 그리드 (voxel grid) 상에서 인접한 8개의 복셀로 구성되는 단위 육면체이다. 엣지 테이블 (edge table) 은 등가면과 엣지의 교차점을 표시하는 테이블이고 셀 테이블 (cell table) 은 등가면에 의해 각 셀에서 추출되는 삼각형의 개수를 저장하는 테이블이다. 링 테이블(ring table)은 삼각형 메시에서 각 정점을 공유 하는 삼각형들을 저장하는 테이블이다. 그리고 검색 테이블 (lookup table) 은 셀에서 등가면에 의해 추출되는 삼각형의 패턴이 저장된 마칭큐브의 테이블을 의미한다.

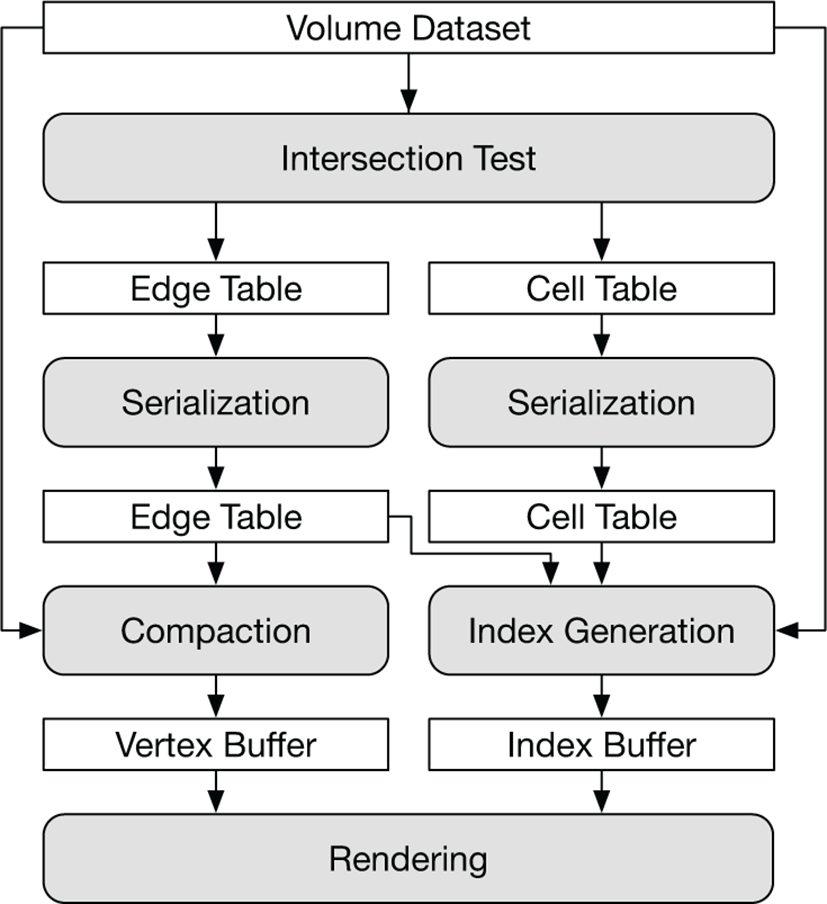
본 논문의 방법은 OpenCL을 사용한 GPU 기반의 마칭큐브 기 법으로 전체적인 과정은 그림 1과 같다. 각 단계는 GPU에 의해 병렬 처리되는 개별적인 커널로 구성하였고, 각각의 커널은 그림 1의 순서에 따라 순차적으로 수행된다. 첫 번째 단계인 교차점 검사 과정에서는 엣지와 등가면이 만나는 지점을 엣지 테이블에 저장하고, 각 셀에서 생성되는 삼각형의 개수를 셀 테이블에 저장한다. 두번째 단계는 직렬화 단계로 엣지 테이블과 셀 테이블의 구간 합을 계산하여 각 각의 교차점과 삼각형 리스트에 순차적인 인덱스를 부여한다. 그 후에 엣지 테이블을 압축하여 정점 버퍼를 생성하고, 엣지 테이블과 셀 테이블을 참조하여 인덱스 버퍼를 생성한다. 그리고 후처리 과정으로 곡률 추정 (curvature estimation)등 에서 사용하는 1-링 구조[3]와 지오메 트리 셰이더에서 사용하는 인접 삼각형을 포함하는 인덱스 구조 (GL_TRIANGLE_ADJACENCY) 를 생성한다.

4.1 교차점 검사 (intersection test)

이 단계에서는 교차점 검사와 셀 검사를 수행하고 결과를 엣지 테이블과 셀 테이블에 저장한다. 두 테이블은 추후에 정점 버퍼와 인덱스 버퍼를 만들 때 사용된다.

교차점 검사는 등가면과 각 셀이 만나는 교차점 존재 여부를 엣지 테이블에 저장한다. 이 과정에서 실제 교차점의 좌표는 계산하지 않는다. 교차점은 항상 셀의 엣지 상에만 존재하므로, 공간상의 모든 셀의 엣지에 대해 교차점을 가지는지를 검사한다. 엣지 테이블은 공간상에 존재하는 모든 엣지를 순차적으로 표현하는 테이블이며, 엣지의 순서는 그림 2의 (a) 와 같이 각 셀의 원점에서의 x, y 그리고 z축과 평행한 엣지 순이다. 셀 검사는 각 셀 안에서 추출되는 삼각형의 개수를 셀 테이블 저장한다. 셀에서 추출되는 삼각형의 개수는 마칭큐브의 검색 테이블을 참조하여 얻을 수 있다. 본 기법은 보다 효율적인 연산을 위해 검색 테이블의 첫 번째 열에 추출되는 삼각형의 개수를 추가하였다.

Figure 1: Overview of our method.

Download Original Figure

전통적인 마칭큐브는 일부 특수한 상황에서 퇴화 삼각형 (degenerate triangles) 이 생성되는 문제점이 있다. 이러한 문제는 대부분 등가면이 격자점 위에 형성될 때 발생하는데, 삼각형 간의 연결정보를 훼손할 수 있다. 특히 5절에서 다룬 인접삼각형 구조의 경우 퇴화삼각형 때문에 잘못된 인덱스 정보가 생성될 수 있다. 이를 회피하기 위해 본 논문에서는 등가값과 동일한 값을 가지는 복셀에 대해 충분히 작은 노이즈를 추가하여 등가면이 격자점 위에서 형성되지 않도록 하였다.

4.2 직렬화 (serialization)

엣지 테이블의 교차점들은 매우 희소하므로, 엣지 테이블을 그 대로 정점 버퍼로 사용하는 것은 비효율적이다. 따라서 엣지 테이블을 직렬화하여 모든 교차점에 순차적인 인덱스를 부여하고 개수를 파악한다. 직렬화 과정은 엣지 테이블 내의 교차점들에 대해서 구간 합을 통해 쉽게 구현될 수 있다. 이렇게 직렬화 된 엣지 테이블은 압축 과정을 거쳐 정점 버퍼로 만들 수 있다. 셀 테이블도 추출되는 삼각형의 개수를 파악하기 위해 직렬화 과정 을 수행한다. 이 단계에서의 직렬화는 Parallel Prefix Sum[9]의 방법을 사용하였다.

Figure 2: Generation of the cell and edge tables. The cell table stores the number of triangles which are extracted from each cell, and the edge table stores the intersection of each edge and the isosurface.

Download Original Figure

4.3 압축 (compaction)

이 단계에서는 직렬화된 엣지 테이블을 압축하여 정점 버퍼로 만들고 각 정점의 교차점 좌표 및 법선 벡터를 계산한다. 교차 점의 좌표는 각 셀의 원점과 x, y 그리고 z축의 인접한 복셀을 선형보간하여 계산한다. 직렬화된 엣지 테이블은 각 엣지들이 고유한 값을 가지고 있으므로, 이를 값을 사용하여 교차점이 저장될 정점 버퍼의 위치를 결정한다. 이 과정에서 각 교차점은 전체 공간에서 개별적인 값들이므로 교차점 단위로 병렬로 처리가 가능하다. 그리고 교차점의 법선 벡터는 유한차분 (finite difference) 으로 근사한다.

4.4 인덱스 버퍼 생성 (index buffer generation)

이 과정에서는 마칭큐브의 검색 테이블을 참조하여 인덱스를 생성한다. 이 과정은 셀 단위로 병렬로 수행되는데, 각 셀에서 삼각형의 패턴은 볼륨데이터와 마칭큐브의 검색 테이블을 통해 얻을 수 있다. 각 삼각형을 구성하는 정점들의 인덱스는 엣지 테이블을 참조하여 얻을 수 있는데, 이를 통해 중복된 위치의 정점들을 하나의 인덱스로 표현함으로써 삼각형 간의 연결정보를 표현할 수 있게 한다. 직렬화 된 셀 테이블의 삼각형을 포함하는 셀들은 서로 다른 값을 가지므로, 이 값을 통해 인덱스 버퍼에 쓰여지는 위치를 결정할 수 있다. 최종적으로 생성된 인덱스 버퍼는 삼각형들이 정점을 공유하는 메시 구조를 표현할 수 있기 때문에, 삼각형 집합에 비해 보다 쉽게 다양한 고급 렌더링 응용에 활용될 수 있다.

5 후처리 과정

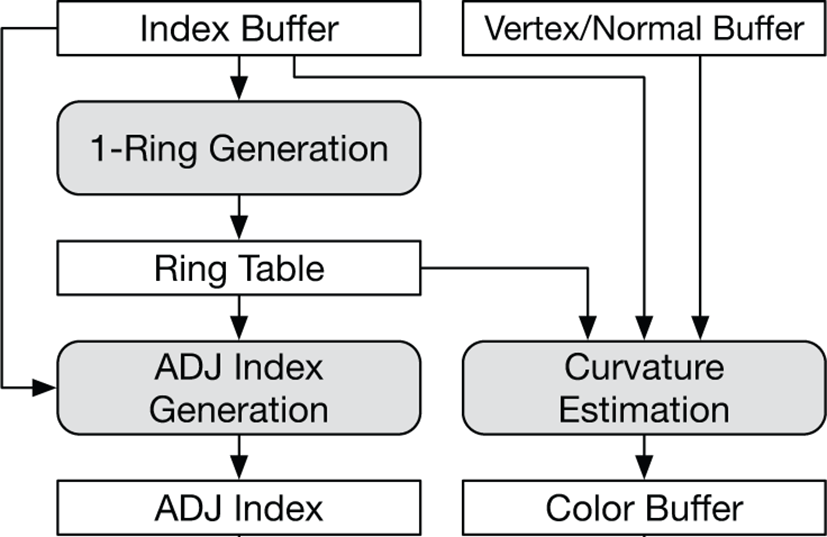
상기 단계에서 추출된 메시는 삼각형의 연결정보가 남아 있기 때문에 다양한 기하학적인 정보를 쉽게 추출할 수 있다. 이 정보를 통 해서 다양한 렌더링 응용에 활용할 수 있는데, 본 절에서는 Griffin 의 GPU 기반 곡률 추정 알고리즘[3] 과 OpenGL 의 지오메트리 셰이더에서 사용되는 GL_TRIANGLE_ADJACENCY 구조의 응용을 소개한다. 전체적인 후처리 과정의 과정은 그림 3와 같다. 그림 3의 ADJ Index는 GL_TRIANGLE_ADJACENCY 구조의 인덱스 버퍼이고, 그림 3의 Color Buffer는 등가면의 곡률을 색상 정보로 표현한 버퍼이다. 두 버퍼를 만드는 전체 과정은 응용에 따라 선택적으로 수행될 수 있다.

Figure 3: Postprocessing

Download Original Figure

5.1 1-링 테이블 생성 (1-ring table generation)

Griffin의 GPU기반 곡률 추정 알고리즘[3] 은 곡률을 계산하기 위해 1-링 구조의 메시 연결 정보를 사용한다. 이 구조는 정점을 기준으로 각 정점을 공유하는 삼각형의 리스트로 메시의 인덱스 버퍼를 사용하여 보다 쉽게 생성할 수 있다. 본 논문에서는 Chen [8] 이 소개한 방법을 간소화하여 사용하였다.

링 테이블의 크기는 전체 정점의 개수와 삼각형 메시의 최대 원 자가 (valence) 에 의해 정해진다. 원자가는 한 정점이 공유하는 삼각형의 개수인데, 삼각형 메시의 최대 원자가는 마칭 큐브의 탐색 테이블을 구현하는 방법에 따라 달라질 수 있다. 링 테이블 의 값을 채우는 과정은 삼각형 단위로 병렬로 수행된다. 따라서 한 정점을 공유하는 다수의 삼각형들이 데이터를 병렬로 쓰는 과정에서 충돌이 발생할 수 있다. 이를 해결하기 위해 링 테이블의 첫 번째 열에 현재까지 추가된 삼각형의 개수를 저장하고, 이를 원자단위 연산 (atomic operation) 을 통해 동기화하였다 (그림 4, 알고리즘 1 참고). 정점을 공유하는 삼각형들은 이 값을 참조하여 고유한 위치에 값을 저장할 수 있다. 링 테이블에 추가 된 삼각형들은 1-링 구조에서의 순서로 정렬되어 있지 않지만, 곡률을 계산할 때는 문제가 발생하지 않는다.

Figure 4: Generation of the 1-ring neighbor table. (a) Traditional triangular mesh, (b) the index buffer, (c) the 1-ring table. The 1-ring neighbor table is generated from the index buffer. The second column of the 1-ring neighbor table is the number of triangles which share a same vertex, and they are synchronized with the atomic operation.

Download Original Figure

Algorithm 1

1-ring neighbor table generation

1: Input: Index Buffer I

2: Output: 1-Ring Table R

3: forfid in faces do

4: forvid in I[fid] do} in parallel

5: p ← atomic_increase(R[vid][0])

6: R[vid][p] ← fid

5.2 인접 삼각형을 포함하는 메시 생성 (adjacency index buffer generation)

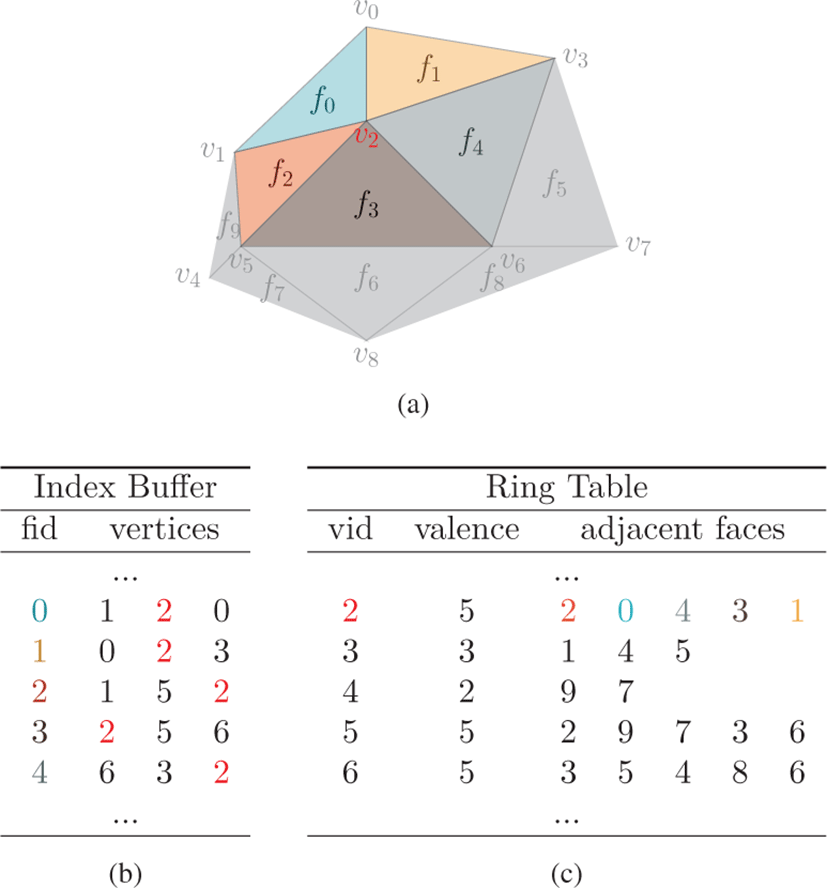
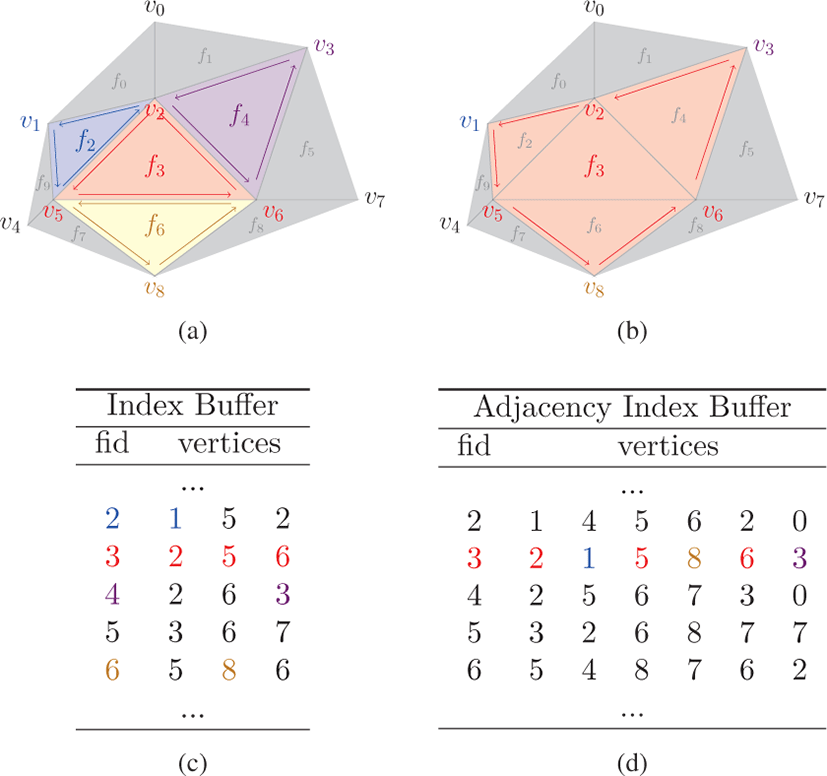
일부 렌더링 기법들은 지오메트리 셰이더에서 사용되는 GL_TRIANGLE_ADJACENCY 형태의 메시 구조를 필 요로 한다. 이 구조는 각각의 삼각형이 인접한 삼각형들에 대한 정점 정보까지 표현하는 구조로 실루엣 렌더링 기법[14] 등에서 활용되고 있다 (그림 5의 (b) 참고). 본 논문의 방법은 이러한 구조의 삼각형 메시를 후처리 과정에서 추출할 수 있도록 하였다 (그림 5 의 ADJ Index). 이 과정은 5.1절에서 생성한 링 테이블과 인덱스 버퍼를 입력으로 받고, 인덱스 버퍼의 각 삼각형으로부터 GL_TRIANGLE_ADJACENCY 형태의 인덱스를 병렬로 생성한다. 그림 5의 (a) 에서 f₃ 는 f₂, f₄ 그리고 f₆ 와 인접하고 있으며, 이 과정을 거쳐 우측의 f₃ 와 같이 확장된다. 이를 위해선 v₁, v₃ 그리고 v₈ 의 인덱스를 찾아야 하는데, 링 테이블에서 v₂, v₅ 그리고 v₆ 의 인접 삼각형들의 리스트에서 얻을 수 있다. 실제 구현에서는 링 테이블을 정점 단위로 병렬처리하고 각 쓰레드들이 정점을 공유하는 삼각형들을 순회하면서 인접한 삼각형에 값을 추가하도록 하였다(알고리즘 2의 4번부터 8번 라인 참고). 예를 들어 f₃ 를 확장하기 위해 추가적으로 필요한 v₁ 은 v₂ 를 공유하는 삼각형들을 처리하는 쓰레드에 의해 쓰여진다. 해당 쓰레드는 우선 v₂ 에서 시작하고 v₅ 에서 끝나는 엣지를 기준으로 그 반대 방향의 엣지를 가지는 삼각형 f₂ 를 링 테이블에서 찾는 다. 그리고 f₂ 의 엣지중 v₂ 에서 시작하는 엣지로 f₃ 를 확장한다 (그림 5, 알고리즘 2 참고).

Algorithm 2

adjacency index buffer generation

1: Input: Ring Table R, Index Buffer I

2: Output: Adjacency index buffer A

3: for allv_i in R do in parallel

4: forf_α in R[v_i] do

5: find f_β in R[v_i] such that $v i v j → ∈ I [f α] Λ v i v j → ∈ I [f β]$

6: add I[f_β] \ {v_j} to A[f_α]

Figure 5: Generation of a mesh with adjacent triangle information. (a) Traditional triangular mesh, (b) a mesh with adjacent triangles, (c) an index buffer, and (d) an adjecy index buffer.

Download Original Figure

6 실험 결과

이 절에서는 본 논문의 방법을 구현하여 실험한 결과를 소개한다. 실험 환경은 Intel i5-4690 @ 3.5GHz CPU와 NVIDIA GeFroce GTX 960 GPU로 구성하였다. 성능비교에는 Hydrogen Atom 과 Test Spheres 볼륨 데이터를 사용하여 기존의 마칭큐브와 비교하였고, 렌더링 실험에서는 Standford Bunny, Armadillo 와 Blob 시뮬레이션을 사용하였다.

6.1 성능 비교

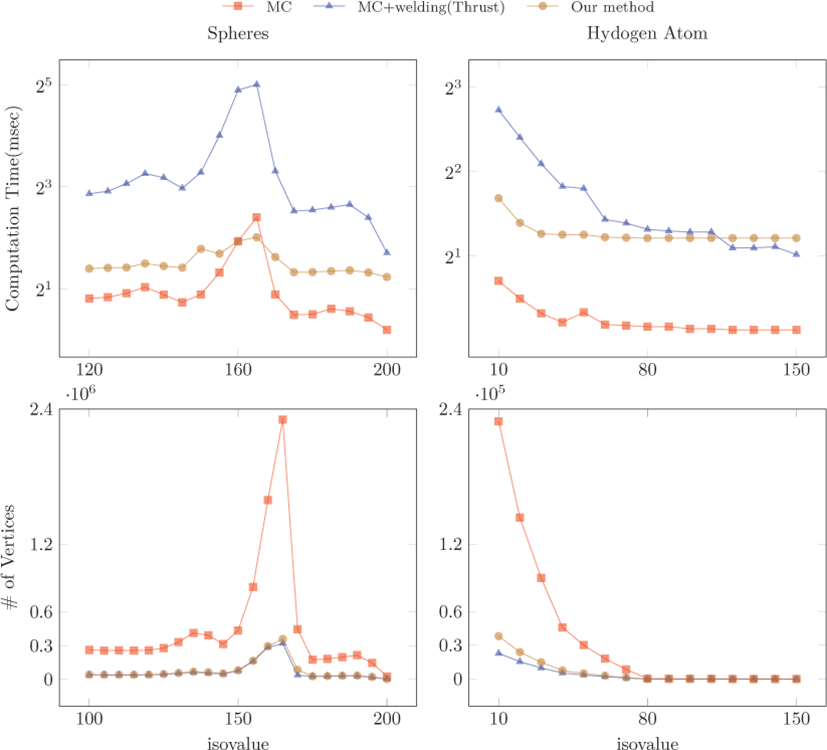
비교 대상은 CUDA SDK에 포함된 GPU 기반의 마칭큐브와 인접한 삼각형들을 연결하는 후처리 과정을 추가한 것이다. 기존 기법에 적용한 후처리 과정은 Thrust로 구현하였다[2]. 실험에 사용한 모델은 128³ 크기의 Spheres와 Hydrogen atom이다. 그 림 6,7을 보면 기존의 마칭큐브는 대체로 연산속도가 가장 빠르 지만 중복된 정점이 많아 전체 정점의 개수가 많은 것을 알 수 있다. 특히 Spheres 모델은 특정 등가값에서 등가면이 복잡하게 형성되어 매우 많은 정점과 삼각형을 생성하는데 (그림 7의 (b) 참고), 기존의 방법은 생성되는 정점의 개수에 영향을 받아 계산 시간이 증가하는 것을 확인할 수 있다. 그리고 후처리를 통해 정점을 연결할 때에는 레벨 값에 따라 성능의 편차가 더욱 심해지는데, 이는 후처리 과정이 정점의 개수에 영향을 많이 받기 때문이다. 이에 비해 본 논문이 제안하는 방법은 중복된 정점이 제거되어 레벨 값에 상관없이 상대적으로 안정적인 성능을 보 인다. 이러한 장점은 실시간 렌더링에 보다 유연하게 응용될 수 있으며 우수한 성능을 기대 할 수 있다.

반면 메모리 사용양은 기존의 방법에 비해 높은 것을 확인 할 수 있다 (표 1 참고). GPU 메모리의 경우 메인 메모리에 비해 크기가 상대적으로 작기 때문에 다소 큰 볼륨 데이터는 제한될 수 있으나, 다양한 모델을 실험한 결과 일반적으로 많이 사용되는 2⁶ ~ 2⁹ 크기의 볼륨 데이터를 처리할 때에는 문제가 없었다.

Table 1: Memory usage(MB). GPU marching cubes technique requires to pre-allocate the memory without knowing the number of triangles. Therefore the memory usage may vary widely depending on the initial setting but usually is proportional to the resolution of the volume dataset.

dimension	MC	Our method
64³	17	34
128³	90	162
256³	520	873

Download Excel Table

6.2 렌더링

본 논문의 방법은 다양한 실시간 렌더링에 응용될 수 있다. 이 절에서는 널리 사용되는 NPR(non-photorealistic rendering) 기법 중 곡률과 실루엣 렌더링에 응용한 결과를 소개한다. 그림 8은 퐁쉐이딩 (phong-shading), 실루엣 렌더링, 곡률 렌더링 그리고 혼합한 형태의 결과이다. 실루엣 렌더링은 5.2의 인접 삼각형 정보를 가지는 삼각형 메시를 입력으로 하는 지오메트리 셰이더를 사용하는 방법[14] 으로 구현하였고, 곡률은 Griffin 의 방법[3] 을 구현하였다. 표 2은 각 방법의 FPS(Frame Per Second) 로 실시간 렌더링에 효율적으로 응용될 수 있음을 보인다. 특히 blob 데이터의 경우 시뮬레이션을 위한 추가적인 전처리 과정이 필요하여 상대적으로 낮은 FPS를 보이지만, 실시간 렌더링에 적용하기에 충분한 성능을 보였다.

Figure 6: Computation time(upper) and number of vertices(lower) for various isovalues(x axis).

Download Original Figure

Figure 7: Extracted isosurfaces for various isovalues of original method(upper) and our method(lower).

Download Original Figure

Table 2: Frame rates of various rendering effects

model	dimension	PS	SR	CR	SR+CR
blob	64³	594	458	473	411
blob	128³	146	127	122	110
armadillo	128³	240	221	195	179
bunny	128³	241	214	204	190

Download Excel Table

Figure 8: Rendered images of (top) Blob simulation, (middle) Armadillo, and (bottom) Stanford bunny. PS, SR, and CR each denotes Phong-shading, silhouette rendering, and Gaussian curvature estimation, respectively.

Download Original Figure

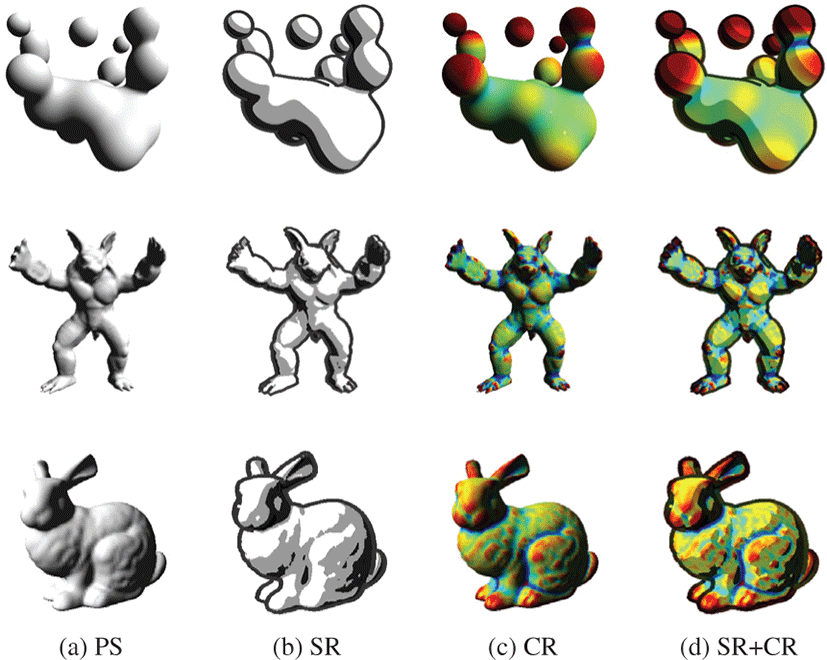
7 한계점

본 논문의 마칭큐브기법은 전체 과정이 GPU상에서 이루어지므로 그래픽스 하드웨어의 사양에 따라 제한될 수 있다. 그래픽스 메모리는 주기억장치에 비해 크기가 작기 때문에 일부 그래픽스 하드웨어에서는 매우 큰 볼륨 데이터를 처리하는 것이 불가능할 수도 있다. 특히 엣지 테이블의 경우 입력된 볼륨의 3배에 달하는 메모리를 요구하므로 이러한 테이블들을 마칭큐브 과정에서 유지할 수 있을 정도의 그래픽스 메모리가 필요로 한다. 따라서 본 논문의 기법은 매우 큰 볼륨 데이터를 다루는 것은 제한될 수 있다. 하지만 일반적인 크기의 볼륨 데이터에 대해서는 큰 문제가 없음을 6.1절에서 확인할 수 있다. 그리고 본 기법에서 사용되는 그래픽스 메모리는 마칭큐브 과정에서만 사용되므로, 시뮬레이션이나 렌더링과 같은 전처리 또는 후처리 단계의 GPU 연산 시에 큰 영향을 주지 않는다.

8 결론 및 향후 연구 과제

본 논문의 기법은 GPU에서 등가면을 삼각형 메시로 추출하는 것으로, 삼각형 집합 형태의 등가면 추출기법과 비교하여 삼각형 의 기하 정보를 후처리 과정 없이 일정한 성능으로 얻을 수 있는 큰 장점이 있음을 보였다. 따라서 본 기법은 곡률과 같은 기하 정보를 사용하는 일부 실시간 렌더링 기법에 응용이 가능하다. 하지만 기존 방법에 비해 더 많은 메모리를 요구하는 단점이 존재하며, 매우 큰 볼륨에 대해서는 효과적인 등가면 추출이 제한되는 단점이 있다. 또한 본 논문의 방법은 기존의 마칭큐브를 기반으로 한 것으로, 현재 널리 사용되고 있는 듀얼마칭큐브 (dual marching cube)[15] 와 같은 적응격자 (adapative lattice) 에서의 마칭 기법은 고려하지 않았다. 향후에는 이러한 부분들을 보완하고 BCC(Body Centered Cubic)와 같은 이종 격자에서의 마칭 기법에 대한 후속 연구를 계획 중이다.

감사의 글

이 논문은 2016년도 서울시립대학교 교내학술연구비에 의하여 지원되었음.

참고 문헌

[1].

W. E. Lorensen and H. E. Cline, “Marching cubes: A high resolution 3d surface construction algorithm,” in ACM siggraph computer graphics, vol. 21, no. 4. ACM, 1987, pp. 163–169.

[2].

N. Bell, “High-productivity cuda development with the thrust template library,” in GPU technology conference, 2010.

[3].

W. Griffin, Y. Wang, D. Berrios, and M. Olano, “GPU curvature estimation on deformable meshes,” in Symposium on Interactive 3D Graphics and Games. ACM, 2011, pp. 159–166.

[4].

R. S. Gallagher, “Span filtering: an optimization scheme for volume visualization of large finite element models,” in Proceedings of the 2nd conference on Visualization’91. IEEE Computer Society Press, 1991, pp. 68–75.

[5].

G. H. Weber, G. Scheuermann, and B. Hamann, “Detecting critical regions in scalar fields,” in VisSym, vol. 3, 2003, pp. 85–94.

[6].

H. Carr, J. Snoeyink, and M. van de Panne, “Simplifying flexible isosurfaces using local geometric measures,” in Visualization, 2004. IEEE. IEEE, 2004, pp. 497–504.

[7].

C. Dyken, G. Ziegler, C. Theobalt, and H.-P. Seidel, “High-speed marching cubes using histopyramids,” in Computer Graphics Forum, vol. 27, no. 8. Wiley Online Library, 2008, pp. 2028–2039.

[8].

J. Chen, X. Jin, and Z. Deng, “GPU-based polygonization and optimization for implicit surfaces,” The Visual Computer, vol. 31, no. 2, pp. 119–130, 2015.

[9].

M. Harris, S. Sengupta, and J. D. Owens, “Parallel prefix sum (scan) with cuda,” GPU gems, vol. 3, no. 39, pp. 851–876, 2007.

[10].

C. Dyken, S. Norway, and G. Ziegler, “GPU-accelerated data expansion for the marching cubes algorithm,” in GPU Technology Conference Presentations, 2010.

[11].

R. Geiss, “Generating complex procedural terrains using the gpu,” GPU gems, vol. 3, pp. 7–37, 2007.

[12].

R. Wenger, Isosurfaces: geometry, topology, and algorithms. CRC Press, 2013.

[13].

G. E. Blelloch, “Prefix sums and their applications,” 1990.

[14].

D. Wolff, OpenGL 4.0 shading language cookbook. Packt Publishing Ltd, 2011.

[15].

S. Schaefer and J. Warren, “Dual marching cubes: Primal contouring of dual grids,” in Computer Graphics and Applications, 2004. PG 2004. Proceedings. 12th Pacific Conference on. IEEE, 2004, pp. 70–76.