액체 시뮬레이션의 얇은 특징을 빠르게 표현하기 위한 CPU와 GPU 이기종 컴퓨팅 기술

1. 서론

유체와 고체의 상호작용으로부터 표현되는 디테일한 유체의 난류를 표현하는 것은 물리 기반 시뮬레이션 분야에서 핫이슈이다. 특히, 난류를 포함하는 유체를 애니메이션 할 때 세밀한 디테일을 생성하고 표현하는 것은 굉장히 중요한 부분이다.이 문제를 개선하기 위해 많은 기법들이 제안되어 왔다. 물리기반 [1, 2, 3], 노이즈와 텍스쳐 기반 [4, 5, 6] 기법들은 유체 시뮬레이션 분야에서 꾸준히 소개되어 왔다.

적응형 격자와 멀티그리드 방법들은 유체 시뮬레이션에서다양하게 표현되는 난류 흐름을 모델링하기 위해 널리 사용되었다 [7, 8, 9]. 더 높은 해상도를 갖는 격자공간에서 Navier-Stokes 방정식을 풀어냄으로써 작은 디테일의 와류 현상을일시적으로 표현할 수 있다. 그러나 와류가 고해상도 격자공간에서부터 멀어지면 그 디테일한 움직임을 보존하기 어려워진다. 이러한 문제를 해결하여 작은 난류의 움직임까지 표현하고자, 격자가 아닌 입자들을 이용하여 와류를 표현하는 하이브리드 프레임워크 기법들이 소개되어왔다 [10, 11].

Muller et al.가 제안한 SPH(Smoothed particle hydrodynamics)기법 [12] 이후로 입자 기반 시뮬레이션 분야는 많은 발전이있었다 [13, 14, 15]. 기존의 입자 기반 방법은 거품이나 스플래시 애니메이션에는 적합하지만 스프링력(Spring force)으로 인한 진동문제가 발생하기 때문에 얇은 유체의 특징을 표현하기에는 충분하지 못하다. 격자–입자 하이브리드 접근법들이 많이 제안되었지만 유체의 얇은 특징을 표현하기에는 충분하지 않으며 [16, 17, 18], 격자의 해상도나 입자의 개수를많이 사용하여 표현될 수 있는 접근법 또한 큰 계산량을 요구하기 때문에 실제로 유용하게 사용되지 않는다.

본 논문에서는 액체의 얇은 특징을 보존하는 새로운 입자 기반 CPU–GPU 이기종 프레임워크를 소개한다. 제시된 방법을사용하면 유체 표면의 추적뿐만 아니라 얇은 표면이 사라지는 부분을 찾아내고 새로운 입자를 추가하거나 삭제할 수 있다. 우리는 Particle-in-cell(PIC)/Fluid-implicit-particle(FLIP) 방법을 기반 유체 해법으로 사용하며, 결과적으로 입자기반 유체 시뮬레이션에서 표현되는 얇은 유체의 특징을 캡처하는 CPU–GPU 이기종 프레임워크이다 (그림 1 참조). 얇아서 소실되는액체의 표면은 새로운 유체입자를 추가하여 보존하고, 추가된 입자는 유체의 얇은 특징이 추출될 수 있는 부분이 아닌 곳(예: Deep water 영역)에 들어가면 제거된다. 본 연구는 Yu and Turk이 제안한 이방성 커널 방법에 영향을 많이 받는다 [19]. 이 방법은 주변 입자들의 위치를 이용하여 PCA를 수행하고, 결과적으로 날카롭고 매끄러운 유체표면을 복원하기 위해 입자의 신축(Stretch)과 방향(Orientation)을 계산한다. 우리는 GPU 기반 솔루션을 활용하여 PCA를 수행하고 [20], 유체입자를 삽입할지 여부를 결정하는 기준으로 이 신축 값을 사용한다.

Figure 1: Water splash by our method with CPU-GPU heterogeneous framework. Right two columns in (b): A visualized splash with particles. A thin surface generated by GPU-based anisotropic kernels.

Download Original Figure

2. 관련 연구

액체의 최신 표면추적 기술은 두 가지 접근 방식으로 분류 할수 있다: Implicit 방법과 Explicit 방법. Osher and Sethian [21]이 제안한 Level-set 방법은 가장 널리 사용되는 Implicit 방법중 하나이다. Level-set 방법에서는 각 그리드 노드에서 가장가까운 표면 위치로부터 거리 함수를 계산하고, 거리 값이 0인 곳에서 암시적(Implicit)으로 표면을 정의한다. 이 방법은 그동안 다양한 측면에서 개선되고 수정되었다. Enright et al. [22], Wang et al. [23], and Mihalef et al. [24]은 Lagrangian 입자를 배치하여 수치적 손실을 막았다. Bargteil et al.은 정확한 유체의표면을 추적하기 위해 복원된 표면메쉬로부터 부호거리장을 업데이트하는 방법을 제안했다 [25]. Heo and Ko는 스펙트럼으로 정제된 Level-set과 고차 재 초기 방법(High-order reinitial-ization)으로 유체 표면의 디테일을 보존했다 [26]. 위와 같은Implicit한 방법을 고해상도 격자에서 풀게되면 전반적인 유체의 디테일을 높일 수 있다. 그러나 이러한 접근법을 활용하여도 유체의 얇은 막과 같은 특징을 캡처하기에는 충분하지 않다.

Explicit한 접근법 중 Hirt and Nichols [27]는 전체 셀에 대해서 유체의 비율을 이용하는 Volume of fluid(VOF) 기법을 제안하여 불연속적인 인터페이스를 효율적으로 표현하였다. 좀더 다른 방향으로는 지난 수십년 동안 의료 영상 분석 및 유체역학과 같은 다양한 연구분야를 통해 다양한 메쉬 기반(Mesh-based) 표적추적기법들이 제안되었다 [28, 29, 30]. 일반적으로 메쉬 기반 표면추적기법에서는 메쉬의 정점과 같은 명시적인표면 요소들을 유체의 흐름에 따라 이류시킨다. 그러나, 이 방법은 자기 교차(Self-intersection)나 복잡한 토폴리지(Complextopology) 변형은 어렵기 때문에 일반적으로 자주 쓰이는 방법은 아니다. 이러한 문제는 인접한 격자위치를 재 검색하여 다시 샘플링함으로써 해결할 수 있지만, 이 전략은 여러 복잡한 상황을 모두 고려해야 하기 때문에 알고리즘을 복잡하게 만든다. 입자 기반 접근법은 Explicit 접근법처럼 메쉬의 정점을 보유하지 않고 오직 입자를 이용하여 유체의 표면을 표현하기 때문에 알고리즘 측면에서도 복잡하지 않다. SPH 방법 [12, 31, 32], Moving particle semi-implicit(MPS) 방법 [33, 34], Meshless물리 기반 시뮬레이션 [35, 36, 37]과 같은 입자 기반 방법들은 일반적으로 물리 기반 시뮬레이션뿐만 아니라 유체의 표면을 복원하는데에도 종종 사용되곤 한다. Blinn [38], Zhu and Bridson [17], Adams et al. [39], Yu and Turk [19]는 Point cloud로부터 좀 더 정확하게 표면을 복원할 수 있는 방법을 제안했다. 본 논문에서 활용하는 분할 가능한(Splittable) 입자 기반접근법은 적응형 입자 방법의 범주에 속한다. 우리방법과 이 방법의 가장 큰 차이점으로는 유체의 얇은 막과 같은 특징을 지속적으로 유지할 수 있도록 제작된 반면, 다른 하나는 입자의 크기를 다르게 하여 샘플링함으로써 유체의 시각적인 디테일을 유지하면서 계산 비용을 줄이는 것이다.

3. 제안하는 프레임워크

제안하는 방법에서는 FLIP [17, 40]기반의 3차원 유체입자들을 이용하여 유체의 얇은 특징을 생성하고 유지하는 최적화된 CPU–GPU 이기종 프레임워크이며, 이 알고리즘은 아래와 같은 순서로 수행된다.

3.1 이기종 프레임워크를 이용한 액체의 얇은 막유지 기법

3.1.1 얇은(Thin)입자 추출

제안하는 방법은 유체의 막을 유지할 수 있는 Ando의 방법을 기반으로 한다 [40]. 먼저 이방성 커널을 사용하여 입자들의 분포를 분석한다. 입자의 방향성을 추출하기 위해 우선 다음과 같이 입자마다 가중치 평균 공분산 Ci를 계산한다 (수식 1 참조).

$$C_i=\frac{{\displaystyle {\sum }_j\left(p_j-\overline{p_i}\right){\left(p_j-\overline{p_i}\right)}^T{W}_{smooth}\left(p_j-\overline{p_i},{\alpha }_1{d}_0\right)}}{{\displaystyle {\sum }_j{W}_{smooth}\left(p_j-\overline{p_i},{\alpha }_1{d}_0\right)}}$$

(1)

여기에서 d0는 유체입자들 사이의 초기 거리 값이며, α₁은초기 거리 값 d0을 조절하는 변수이다.

$$\overline{p_i}=\frac{{\displaystyle {\sum }_j{p}_j{W}_{smooth}\left(p_j-p_i,{\alpha }_1{d}_0\right)}}{{\displaystyle {\sum }_j{W}_{smooth}\left(p_j-p_i,{\alpha }_1{d}_0\right)}},$$

(2)

$$W_{smooth}\left(r,h\right)=\{\begin{array}{ll}1-{\Vert r\Vert }^2/h^2,\hfill & 0\le \Vert r\Vert \le h,\hfill \\ 0,\hfill & \text{otherwise}\text{.}\hfill \end{array}$$

(3)

위 수식들을 사용하여 계산된 공분산 행렬 C_i와 SVD(Singular value decomposition)를 이용하여 입자의 분포에 대한 고유 벡터와 고유 값을 계산한다. 이 값으로부터 인접 입자 사이의 스트레칭과 방향성을 추출한다.

$$C_i={\left[\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right]}^T\left[\begin{array}{lll}{\sigma }_1\hfill & \hfill & \hfill \\ \hfill & {\sigma }_2\hfill & \hfill \\ \hfill & \hfill & {\sigma }_3\hfill \end{array}\right]\left[\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right],$$

(4)

여기서 e_n은 분산에 의해 추출된 주축 성분을 나타내며 σ_n 는 스트레칭 정도를 나타낸다. 얇은 표면에 존재하는 Thin입자는 σ₃ ≤ α₂σ₁를 검사하여 추출한다. 여기서 α₂는 두께의 정도를 결정하는 임계값이다.

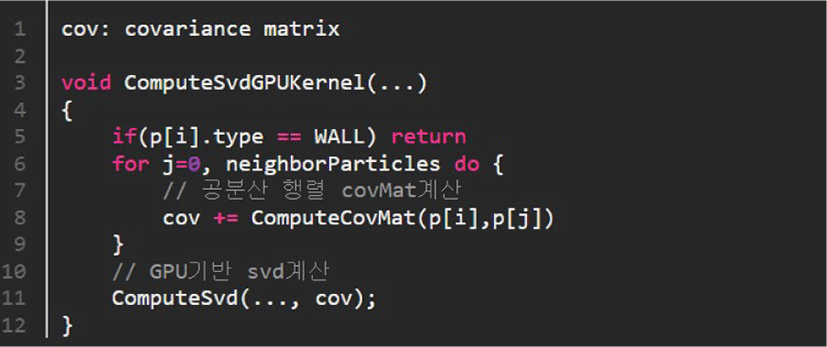
그림 2와 3은 유체입자의 밀도와 공분산 행렬을 이용한 SVD계산까지의 과정을 CUDA kernel로 계산한 Pseudo code이다. 이 과정은 3장에서 설명한 Step1:[GPU]과 Step2:[GPU]에 해당한다. 그림 2는 유체입자의 밀도 값을 이용하여 대략적으로 표면입자를 분류하는 Pseudo code이며 (그림 4 참조), 그림 3은 인접 입자들과의 거리 값을 이용하여 공분산 행렬을 계산하는 Pseudo code이다. 최종적으로 SVD를 이용하여 고유 벡터와 고유 값을 계산하는 부분은 GPU 기반의 병렬 프로그래밍을 통해 계산한다 [20].

Figure 2: Pseudo code for computation of particle density in GPU.

Download Original Figure

Figure 3: Pseudo code for computation of covariance matrix and singular value decomposition in GPU.

Download Original Figure

Figure 4: Selected thin particles from water particles (thin particles are colored violet and lie on the outer edge of the fluid body)

Download Original Figure

3.1.2 후보위치 추출과 최적화

추출된 Thin입자들은 Hole 부분에 새로운 입자를 추가하는데 사용된다. 우리는 Hole을 채워 넣을때 사용하는 입자들의 Pair 인 (i, j)를 찾는다. Pair의 중심 위치인 (p_i+p_j)/2는 분할(Splitting)을 하기 위한 후보위치로 사용하기 위해 저장시키고, 아래 조건을 모두 만족하는 Pair를 최종적으로 선택한다:

$${\alpha }_3{d}_0\le \Vert p_i-p_j\Vert \le {\alpha }_4{d}_0,$$

(5a)

$${\displaystyle \sum _k{W}_{smooth}\left(\left(p_i+p_j\right)/2-p_k,{\alpha }_3{d}_0\right)=0,}$$

(5b)

$$\left(p_i-p_j\right).\left(u_i-u_j\right)>0,$$

(5c)

여기서 α₃와 α₄는 각 후보위치 사이의 최소 거리와 최대 거리를 제어하는 상수이며, u는 입자의 속도이다. 수식 5a는 두입자가 서로 적당한 거리에 있는지 검사하는 것이다. 수식 5b는 반지름 α₃에 새로운 입자를 추가하기에 적당한지를 판단하기 위한 조건이며, 후보위치 주변에 유체입자가 없는지, 다시말해, 희박한 영역인지를 검사하는 것이다. 수식 5c에서는 한 쌍의 유체입자들 사이의 거리가 시간이 지남에 따라 증가하는지 확인한다. 결과적으로 위 조건을 모두 만족하는 Pair의 중간 위치를 중복 없이 S에 저장시킨다.

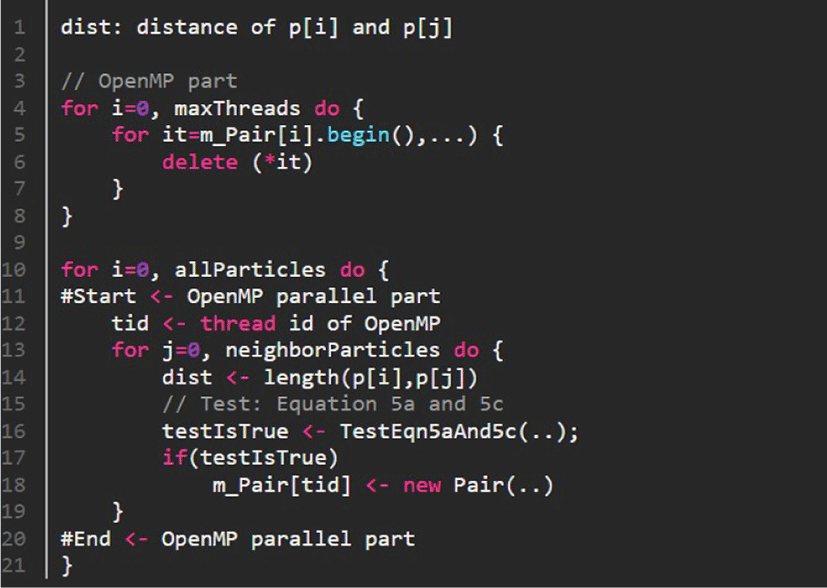
그림 5는 후보위치들을 추출하기 위한 과정을 CPU 기반병렬 모듈로 계산한 Pseudo code이며, 이 과정은 Step3:[GPU]에 해당한다. Ando et al. [40]의 방법에서는 모든 유체입자에 대해서 3가지 조건을 모두 검색하여 중복없이 만족하는 Pair를 찾기 때문에 계산 시간이 오래 걸린다. 우리는 이를 효율적으로 처리하기 위해 CPU–GPU 이기종 병렬 프레임워크로 분할하여 계산한다.

Figure 5: Pseudo code for pair collection in CPU.

Download Original Figure

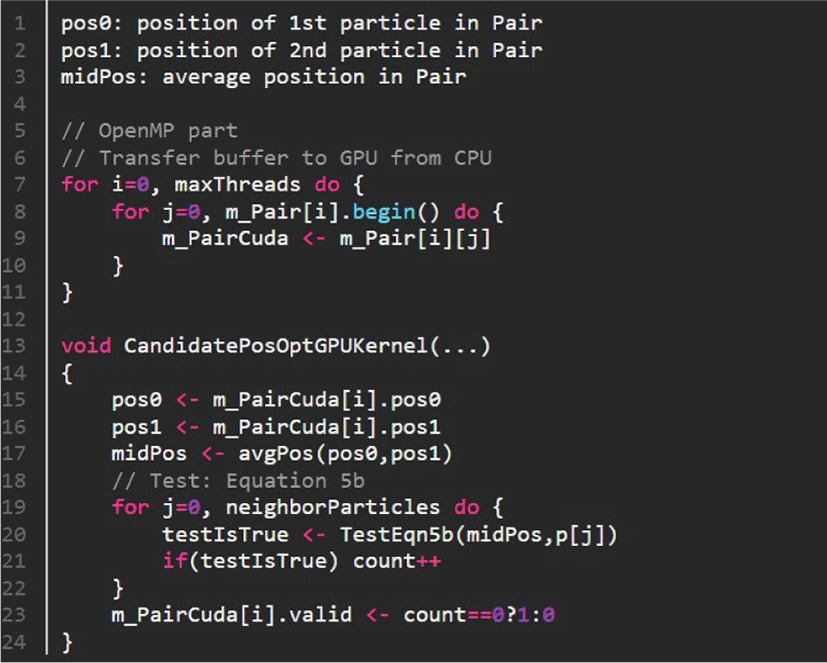
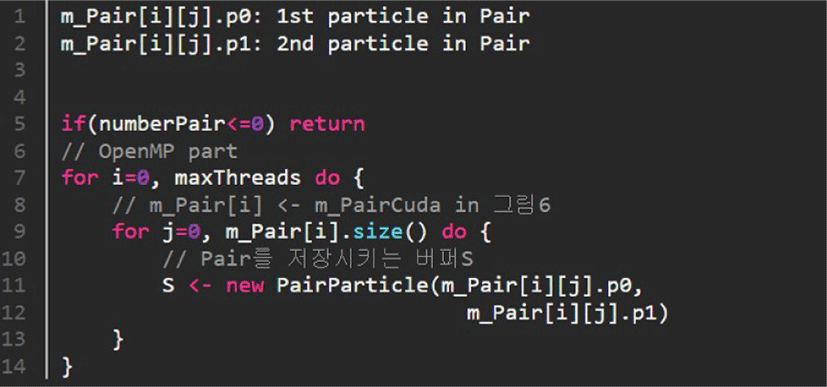
그림 5는 수식 5를 만족하는 Pair를 찾기 위한 과정을 처리하는 Pseudo code이다. 본 논문에서 CPU 기반 병렬처리는 OpenMP를 이용하였으며 CPU에서 제공하는 최대 스레드 개수(omp_get_max_threads())만큼 Pair버퍼를 생성하고, 수식 5a와 5c 조건들을 만족하는Pair를 각 스레드 인덱스에 맞는 Pair버퍼에 저장시킨다 (m_Pair[omp_get_thread_num()]). 이 과정에서 계산된 Pair집합들에서는 많은 수의 후보 Pair들이 추출되기 때문에 모든 인접 입자들을 필요로 하는 수식 5b는 계산 시간이 오래 걸린다. 우리는 이 과정을 효율적으로 계산하기 위해 GPU 기반 병렬처리로 수행한다 (그림 6 참조). 최종적으로 GPU상에서 계산된 Pair버퍼(m_PairCuda)를 CPU로 전달한다(m_Pair[i][]). 그림 7은 이 과정을 수행하는 Pseudo code 이며 결과적으로 S버퍼를 구성한다. 다음 장에서는 이 버퍼를 이용하여 새로운 유체 입자의 추가와 삭제방법을 설명한다.

Figure 6: Pseudo code for optimization of candidate position in GPU.

Download Original Figure

Figure 7: Pseudo code for compuing S buffer in CPU.

Download Original Figure

3.1.3 유체입자 추가와 삭제

추출한 후보위치 리스트인 S의 개수가 많기 때문에 이를 간소화하기 위한 방법이 필요하다. 이번 장에서는 불필요한 유체 입자들을 필터링하고，유체의 얇은 표면을 유지하기 위해 필요한 최소 개수의 유체 입자로 Hole-filling하는 방법에 대해 설명한다. 추가된 후보위치들의 최종 버퍼를 I라고 부르며 지금 부터 이 버퍼를 결정하는 방법을 설명한다. 이 버퍼에서 첫 번째 입자인 I₁에는 S에서 밀도를 기반으로 가장 희박한(Sparse) 후보위치를 저장한다 (수식 6 참조):

$$I_1=\underset{j\in sizeS}{\mathrm{argmin}}\left({\rho }_j{S}_j\right),$$

(6)

여기서 ρ_j는 유체입자 j의 밀도이다. S에서 I₁을 결정한 후, 우리는 sI₁의 주변 입자들로부터 반경이 α₃d₀ 내에 존재하는 후보 입자들을 삭제한다. 다음 단계에서는 sI₁의 주변입자들로부터 반지름α₃ 외부에있는 입자들을 검색하여 NI₁ 에 추가 한다. NI₁ 에 있는 입자들 중 가장 가까운 입자 s_j를 I₂에 추가 한다(수식 7 참조):

$$I_2=\underset{j\in N{}_I{}_{{}_1}}{\mathrm{argmin}}\Vert S_j-S_I{}_{{}_1}\Vert .$$

(7)

I₂가 I₁에서 발견되는 검색방법을 I_n+1 = search(I_n)으로 정립할 수 있고, 이 작업을 반복하면서 I₃, I₄, I₅…, I_n+1를 순차적으로 처리한다. 만약에 검색이 실패하여 적당한 유체입자를 찾지 못하면 수식 6을 대신 사용한다.

유체 입자가 분할된 후에 분할된 각 입자들의 속도와무게 값들은 선형 보간으로 할당된다. 아래 수식을 이용하여 Eulerian 격자에 매핑된 속도 u와 입자의 밀도 ρ를 계산한다:

$$u\left(x\right)=\frac{{\displaystyle {\sum }_i{m}_i{u}_i{W}_{sharp}\left(p_i-x\text{,}{\alpha }_5{d}_0\right)}}{{\displaystyle {\sum }_i{m}_i{W}_{sharp}\left(p_i-x\text{,}{\alpha }_5{d}_0\right)}},$$

(8)

$$\rho \left(x\right)={\displaystyle \sum _i{m}_i{W}_{smooth}\left(p_i-x\text{,}{\alpha }_1{d}_0\right)},$$

(9)

여기서 α₅는 속도 u의 크기를 조절하는 변수이고, W_sharp 커널은 아래와 같다.

$$\nabla W_{sharp}\left(r,h\right)=\{\begin{array}{ll}{h}^2/\Vert r^2\Vert -1,\hfill & 0\le \Vert r\Vert \le h,\hfill \\ 0,\hfill & otherwise\text{.}\hfill \end{array}$$

(10)

추가된 유체 입자 i는 다음 두 가지 중 하나를 만족하면 삭제한다:

$${\rho }_i>{\alpha }_6{\rho }_0\text{ and}{\alpha }_3\ge \alpha 2{\sigma }_1,$$

(11a)

(11b)

여기서 α₆은 최대 밀도계수를 나타내고，α₇은 입자 사이의 최소 거리를 나타낸다. 수식 11을 만족하는 유체 입자들은 모두 삭제를 한다. 이 과정에서 한 번에 많은 양의 입자들이 삭제되면 깜빡거리는 문제가 발생하는데 이를 줄이기 위해 난수 값을 이용하여 삭제되는 시점을 조금씩 다르게 하였다.

이 유체입자를 추가/삭제하는 과정은 I_n이 처리된 다음 I_n+1이 처리 되어야 하는 Serial한 구조이기 때문에 Ando et al. [40]가 제안한 알고리즘과 동일하게 처리하였다.

3.1.4 유체의 표면복원

수식 4의 SVD 값은 이방성 커널에 재사용할 수 있기 때문에 Yu et al. [19] 알고리즘에 재사용하여 얇은 표면을 재구성하는 데 사용한다(수식 12참조).

$$\varphi \left(x\right)=\underset{i}{\min }\left(\Vert G_i\left(p_i-x\right)\Vert \right),$$

(12)

여기서 G_i는 유체입자i에 대한 변형행렬을 나타낸다.

$$G_i=\frac{1}{k_s}{\left[\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right]}^T{\left[\begin{array}{lll}{\sigma }_1\hfill & \hfill & \hfill \\ \hfill & {\sigma }_2\hfill & \hfill \\ \hfill & \hfill & {\sigma }_3\hfill \end{array}\right]}^{-1}\left[\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right]$$

(13)

여기서 k_s는 스케일링 상수이다. 중요한 스트레칭 부분을 보존하기 위해서 σ_n은 일정 범위 내로 제한한다. 좀 더 자세한 설명은 Yu et al. [19] 연구를 참조하길 추천한다. 본 논문에서 는 GPU 기반 Marhcing Cube 알고리즘을 사용했으며 [41], 이 방법과 맞물려서 얇은 유체표면이 잘 캡처되도록 최소 스트레칭을 격자 너비의 절반보다 크게 설정하였다.

Figure 8: GPU-based fluid surface reconstruction.

Download Original Figure

4. 구현

제안된 방법이 구현된 환경은 아래와 같다: Intel i7-2600k 3.40GHz CPU 16GB RAM, NVIDIA GeForce GTX 480 graphics card. FLIP기반 유체해법을 기반액체(Underlying water) 시뮬레이션으로 사용했으며, 유체의 압력을 계산하는 수치적 행렬해법은 GPU 기반 Preconditioned conjugate gradient [42] 방법을 이용하였고, GPU 기반 SVD계산은 Lahabar의 방법을 활용하였다 [20]. FLIP격자의 경우 모든 운동량은 Staggered Marker-and-Cell 방법을 사용하여 저장했으며 [43], 표면 재복원을위해 추가적인 격자를 사용하였다. 물과 고체의 충돌처리를 위해 변량(Variational) 프레임워크를 사용했다 [44].

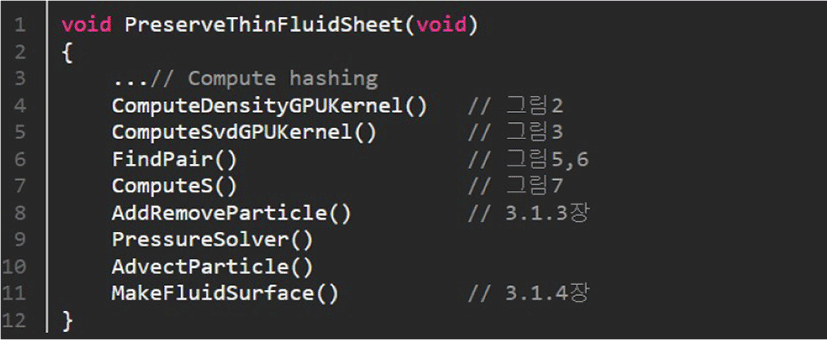
그림 9는 본 논문에서 제안하는 얇은 유체의 특징을 보존하는 알고리즘의 Pseudo code이다. 격자와 유체입자 사이에서 운동량을 전달하거나 압력을 계산하는 모든 전반적인 계산이 CPU와 GPU 기반병렬 프레임워크에서 수행된다.

Figure 9: Pseudo code of our framework.

Download Original Figure

5. 결과

제안하는 프레임워크를 다양한 방면으로 분석하기 위해 5가지 시나리오에서 우리의 방법을 비교했다.

우리는 간단한 테스트 시나리오 상에서 제안하는 기법의 우수성을입증하기 위해 구형 액체를 위에서 떨어뜨리는 장면을 제작했다 (그림 10 참조). 이 장면에서 기반유체를 표현하기 위해 타입 스텝을 0.006으로 설정하고, 30만개의 유체입자들을 사용하였다. 우리의 기법은 CPU 기반 기법인 Ando et al. [40]의 방법과 동일한 결과를 만들어 내면서 결과적으로 ×6배 빠른 결과를 보여주었다. 그림 10에서 보듯이 구형 액체가 메인유체와 충돌 됨에 따라 나타나는 유체의 얇은 막과 필라멘트 (Filaments)를 빠르고 명확하게 표현했다.

Figure 10: Thin sheet surfaces of liquid by our method.

Download Original Figure

그림 11은 제안된 기법의 결과품질을 비교한 결과이다. Zhu and Bridson방법은 얇은 막이 표현되는 부분에서 표면 소실이 많이 일어나며 (그림 11a 참조), 이런 문제를 줄이고자 표면의 Level-set값을 Smoothing 시키면 수치적으로는 좀 나아지지만 시각적으로 개선이 크게 되지 않는다 (그림 11b 참조). 최근에 Bhatacharya et al. [45]은 유체표면을 좀 더 정확하게 캡처하고자 Biharmonic smoothing 기법을 제안했다. 이 논문은 Laplacian smoothing 에 비해 좀 더 부드러운 유체의 표면을 캡처하여 개선된 결과를 보여주지만, 얇은 유체의 막 부분에서 여전히 소실 문제가 발생한다 (그림 11c 참조). 하지만 우리의 방법은 결과적으로 소실 문제를 최소화하여 디테일한 유체의 표면을 표현하였으며, GPU 프레임워크로 기존 방법보다 빠르게 장면을 제작하였다. 장면구성과 성능개선은 그림 10의 결과와 같다.

Figure 11: Comparison results: dropping a liquid sphere.

Download Original Figure

유체의 얇은 표면이 나타나는 디테일한 특징은 고체와 유체가 충돌되는 커플링 장면에서도 쉽게 확인할 수 있다. 제안하는 모델이 커플링 장면에서도 잘 동작한다는 것을 입증하기 위해, 우리는 변형체 모델을 유체에 던져 자연스럽게 스플래시 현상이 나타나도록 하였다 (그림 12 참조). 호박(Pumpkins)모델이 물에 닿는 순간 표현되는 Water crown 형태를 잘 표현한다. 뿐만 아니라 바운더리에 물이 닿았을 때도 유체표면이 깨지지 않고 깔끔하게 유체표면을 표현하였다. 이 장면에서는 120만개의 유체입자들을 사용하였고, Ando et al. [40]의 방법과 동일한 결과를 만들어 내면서 결과적으로 ×10배 빠른 결과를 보여주었다.

Figure 12: Deformable pumpkins thrown from various directionos.

Download Original Figure

제안된 방법을 이용했을 때 실제로 어떤 부분에서 Thin입자들이 추가되어 결과적으로 유체의 얇은 표면을 유지할 수 있는지를 보여주기 위해 Water pouring 장면을 제작하였다. 그림 13a는 Water pouring으로 인해 물이 상단에서 하단으로 떨어지면서 표현되는 유체의 얇은 표면을 보여주고 있으며, 같은 장면에서 유체입자는 그림 13b에서 보여준다. 이 장면은 다른 장면에 비해 유체의 얇은 막이 많이 표현되는 장면이며, 이 같은 특징은 유체입자에서도 컬러로 쉽게 보여진다. 빨간색은 새롭게 추가된 Thin입자이며, 이 입자들로 인해 유체의 얇은 막들이 표현된다. 이 결과는 Ando et al. [40]의 방법에서도 동일하게 만들어 낼 수 있지만, 제안된 기법은 Ando의 기법보다 ×7배 정도 빠른 결과를 보여주었다. 그림 14는 Ando etal. [40]의 결과이며, 제안된 결과는 Ando의 기법과 시각적 비교했을때 큰 차이없이 비슷한 결과를 만들어 냈다. 그림 14a는 Water splash를 표현한 결과이며, 그림 1b와 그림 10의 결과와 비교했을 때 유체의 얇은 막을 잘 표현했다. 그림 14b 또한 그림 13와 비교했을 때 시각적으로 유사한 결과를 만들어 냈다. 유체의 얇은 막을 유지하려는 추가적인 입자들의 개수가 많아지기 때문에 증가되는 계산 시간을 이기종 프레임워크로 최적화하였다. 일반적으로는 압력을 계산하는 Pressure solver부분이 계산 양이 크다는 점과는 다소 차이점이 있다.

Figure 13: Water pouring off a box cliff.

Download Original Figure

Figure 14: Results with Ando’s method [40].

Download Original Figure

그림 15는 물을 박스로 마구 휘젓는 장면이며, 다른 장면들과 마찬가지로 유체의 디테일한 특징을 잘 캡처하였다. 이 장면에서 사용한 유체입자는 약 100만개이며, 우리의 방법은 Ando의 기법보다 ×4배 정도 빠른 결과를 보여주었다.

Figure 15: Water pool interacting wth a stirring box.

Download Original Figure

6. 결론 및 향후 연구

우리는 유체의 얇은 막을 효율적으로 표현하기 위한 CPU–GPU 기반 이기종 프레임워크를 설명했다. 계산양이 큰 부분은 GPU를 이용하였고, 그렇지 않은 부분은 CPU 기반 병렬기법을 사용했다. GPU는 병렬계산을 위해 CPU에서 GPU로 데이터를 복사하고, 계산된 결과를 다시 반영하기 위해 GPU에서 CPU로 다시 복사하는 과정이 추가된다. 우리는 이 불필요한 과정을 줄이기 위해 계산양이 크지 않은 부분은 CPU 기반병렬기법을 사용했다.

앞에서 본 결과들에서 성능개선을 측정하기 위한 방법은 유체의 얇은 막이 계산되는 부분만 측정했으며, 모든 결과에서 Ando et al. [40]의 프레임워크보다 빠른 시간 내에 결과를 만들어냈다. 장면마다 성능개선 정도가 다르지만 제안된 알고리즘은장면 내 Thin입자들의 개수에 비례하여 성능개선이 되었다. 3.1.2장에서 설명한 후보위치의 개수 또한 Thin입자의 개수에 비례해서 생성된다. 결과적으로 제안된 프레임워크는 초기장면에서 생성한 전체 유체입자의 개수와 그로 인해 생성되는 Thin입자의 개수가 제안된 프레임워크의 성능에 영향을 끼쳤다.

제안된 기법의 한계점은 메모리 부족으로 인해 고해상도의 장면을 제작하기 어렵다는 것이다. 유체의 얇은 막을 표현하기 위해서는 초기 장면에 설정된 유체입자의 개수보다 많은 입자들이 필요하며, 장면마다 Thin입자들의 개수가 많이 증가될 수 있다. GPU에서는 가용 메모리의 크기가 제약적이기 때문에 큰 스케일의 장면을 제작하기 위해서는 최적화된 메모리 관리 기법이 필요하며, 향후 우리는 이 메모리 관리를 효율적으로 사용하여 큰 스케일의 유체 시뮬레이션을 모델링 할 수 있는 방법에 대해 연구할 계획이다.