1. 서론
점군 정합(point cloud registration) 이란 하나 혹은 여러 물체를 중 심으로 다중의 장소에서 획득한 점군 데이터를 하나의 공통 좌표 계로 배치시키는 것이다[1]. 이러한 정군 정합은 산업의 여러 분야에 활용되고 있다. 예를 들어, 실제 모델을 평 면 혹은 곡면으로 스캔하여 정합한 점군은 CAD (Computer-aided Design) 모델과 비 교하는 품질 검사에 응용될 뿐 아니 라, 정확한 CAD 모델이 없을 때 에는 정합 모델이 CAD 모델로써의 역할을 하는데, 특히 이 과정은 3차원 프린팅의 전처 리(preprocessing) 과정 이 기도 하다.
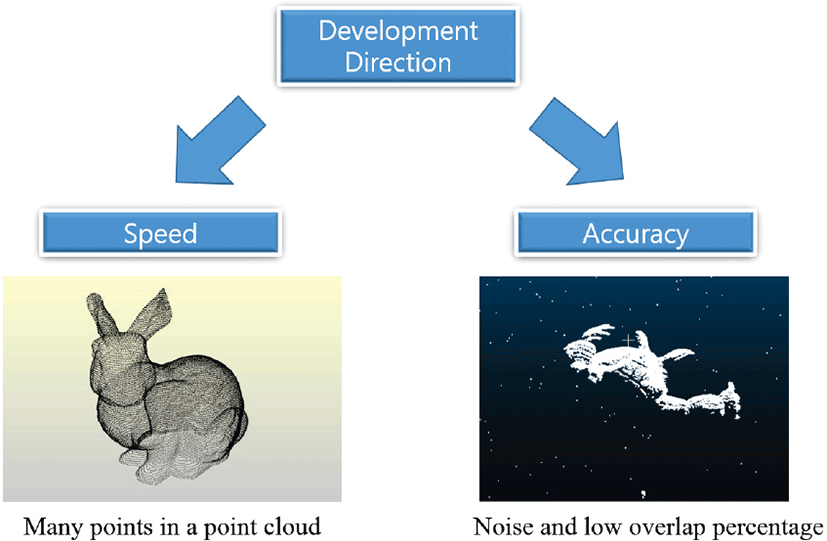
점군을 정합하는 데 있어 그림 1에 나타낸 바와 같이 속도와 정확도가 중요하다. 먼저, 속도에 있어서는, 3차원 스캐너를 사용하여 점이 무수히 많은 점군을 얻으면 각 점들에 대하여 계산을 수행해야 하기 때문에 간단한 연산조차 시간이 많이 걸리는 한계점이 있다. 한편, 정확도는 오버랩과 노이즈의 영향이 크다. 다시 말해 오버랩이 적고 노이즈가 많을수록 정합 정확도를 높이기가 힘들어진다. 그러므로 점군 정합에서는 알고리즘을 간단하게 만들어 속도를 높이고 오버랩 영역을 정밀하게 찾아 정확도를 높이는 것이 중요하다.
본 논문에서는 ICP(Iterative Closest Point) 알고리즘을 사용하 였다. ICP 알고리즘은 초기 정합이 완료된 상태, 즉 점군들이 대략적으로 정렬된 상태에서 강체(rigid) 정합을 하는 데 있어서 가장 강력한 방법이다[1]. 여기에 기하학 기반의 샘플링 방법을 이용하여 정합의 정확도를 향상시키는 알고리즘을 제시하였다. 그리고 정합 속도를 빠르게 하기 위해 가속화 알고리즘을 추가함으로써 정합 속도를 향상시켰다[2].
본 논문의 구성은 다음의 순서를 따른다. 2절에서 정합의 개념을 알아보고 ICP 알고리즘에 대한 원리와 구성, 한계점, 그리고 한계를 극복하기 위한 연구들을 살펴본다. 3절에서는 2절에서 기술한 내용을 바탕으로 본 논문에서 제안하는 방법을 자세히 서술한다. 이에 따른 실험 결과를 4절에서 나타내고 그 결과를 논의하며, 5절에서는 결론과 함께 향후 연구 방향에 대하여 이야기한다.
2. 관련 연구
3차원 공간상의 물체에 대하여 카메라로 어느 한 방향에서 점군 (point cloud) 데이터를 얻는다면, 획득한 데이터는 자체적으로 지역 좌표계 (local coordinate system)를 가진다. 하지만 하나의 데이터만을 획득하는 것으로는 물체에 대한 모든 정보를 알 수 없다. 그래서 그 물체에 대해 각기 다른 여러 방향에서 데이터를 얻는 다. 그리고 이 데이터들을 원래 물체처럼 하나로 나타내기 위해 하나의 전역 좌표계(global coordinate system)로 표현한다. 이렇둣, 여러 점군 데이터의 여러 지역 좌표계를 점군 데이터 세트 하나의 전역 좌표계로 표현하는 과정을 정합이라고 한다[1].
정합은 점군 데이터의 개수에 따라, 데이터가 둘이면 이중 정합(pairwise registration), 셋 이상이면 다중 정합(multiview registration)으로 구분할 수 있다. Besl은 알고리즘의 우수성을 입증하기 위한 수단으로 점 (point set)과 곡선 (curve)과 면 (surface) 에 대하여 각각 이중 정합을 수행하였다[3]. 또, Lee는 멀티 센서를 정합에 충분히 활용할수 있음을 보이기 위해 센서들을 부착한 스캐너로 빌딩 외부를 실제로 스캔하였고 이렇게 획득한 점군들로 이중 정합을 완료하였다[4]. 반면, Pulli는 미켈란젤로의 다비드 조각상을 스캔하고 다중 정합을 진행하기에 앞서 이중 정합을 먼저하고 난 뒤 이를 다중 정합의 제약(constraint)으로 적용하였다[5]. 최근에는 Yun은 선체의 블록을 조립하는 조선 현장에서 스캔한 15개의 점군들로 다중 정합을 수행하였다[6]. 본 논문에서는 다중 정합을 고려하지 않은 채 이중 정합만을 다룬다.
ma개의 점을 포함하는 소스 점군(source point cloud) A를 mb개의 점을 포함하는 타갯 점군(target point cloud) B에 정합한다고 가정하자. 이 때 ICP 알고리즘은 그림 2처럼 여섯 단계로 이루어져\ 있으며, 각 단계는 다음과 같이 요약할 수 있다.
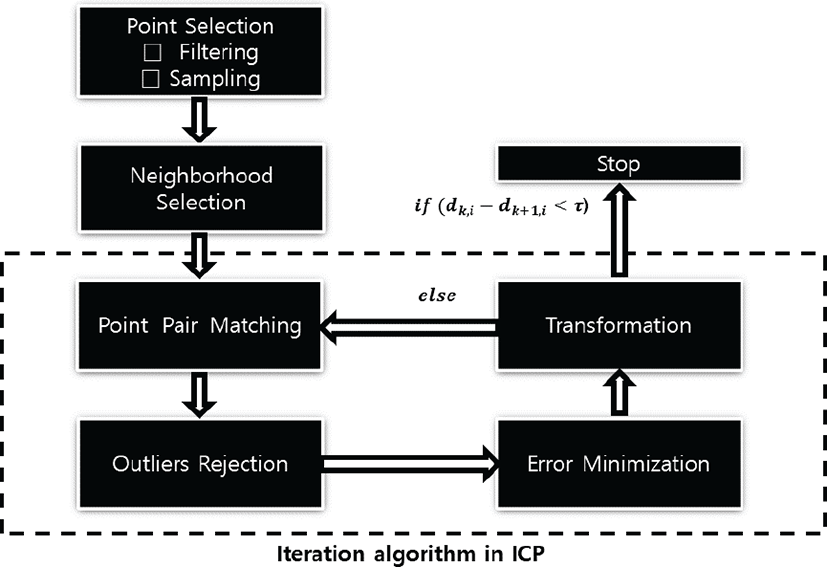
첫째, 점 선택(point selection) 단계에서는 알고리즘의 계산량을 줄이기 위하여 노이즈 필터링이나 샘플링을 거쳐 점의 갯수를 줄인다. 둘째, 이웃 선택(neighborhood selection) 단계에서는 각 점의 주변에 분포하는 점들 중 가까운 점 일부를 선택한다. 셋째, 점쌍 매칭(point pair matching) 단계에서는 앞서 선택한 주변 점들로 곡면(surface)[6]이나 평면(plane)[7] 같은 기하학 요소를 만들고, 이를 이용하여 소스 점군 A의 점 에 대응하는(corresponding) 타갯 점군 표의 점을 찾는다. 넷째, 오정합점 제거 (outlier rejection) 단계에서는 소스 점군 A와 타겟 점군 B에서 서로 겹치는 부분, 즉 오버랩 영역(inlier)만 남기고, 겹치지 않는 영역(outlier) 은 정합에 이용하지 않는다. 다섯째, 오차 최소화(error minimization) 단계 에서는 소스 점군 A의 오버랩 영역 A′과 타겟 점군 B의 오버랩 영역 B′ 방향으로 이동하는 동안 각 대응점의 거리 오차가 최소가 되도록 한다. 여섯째, 변환(Transformation) 단계에서 는 소스 오버랩 점군 A′가 타갯 오버랩 점군 B′의 위치로 이동하 는 데에 필요한병진 행렬(translation matrix)과 회전 행렬(rotation matrix)을 구하여 소스 오버랩 점군 A′에 적용한다. 여기서 거리 오차가 일정한 한계치(tolerance, τ) 이하이면 진행을 멈주고 한계치 이상이라면 점쌍 매칭 (point pair matching) 단계로 되돌아가서 알고리즘을 다시 수행한다.
이러한 ICP 알고리즘은 병진 3자유도와 회전 3자유도를 다루기 때문에 공간상의 모든 방향으로 적용할 수 있는 것은 물론, 점군 데이터의 국소 특징(local feature)이나 전처리(prepocessing)가 필요 없기 때문에 알고리즘이 비교적 간단하다는 장점을 가지고 있다[3]. 하지만 점쌍 매칭 단계에서 대응점 (corresponding point)을 찾는 과정이 알고리즘 1회 수행하는 데에 최대 O(mamb)의 복잡도를 보이는데다가, 오버랩 영역이 매우 적거나 없어 분할된 상태의 점군에 적용하면 정합이 잘못되는 경우가 허다하다[3]. 또, 성게처럼 형상이 복잡하거나[3] 사무용 건물 같이 반복되는 패턴의 경우에도 알고리즘을 적용하기 어렵다.
Besl은 회전 행렬을 구하는 데에 Horn의 최소 자승 사원수 연산(least square quaternion operation)[8]을 이용하여 변환 단계에 적용하였다[3]. 반면, Masuda는 오정합점 제거 단계에서 잔차의 표준 편차(standard deviation of residuals)를 도입하여 이 값의 2.5 배를 거리 임계값(distance threshold)로 설정하였다. 이 때 임계값 이하이면 정합점 (inlier)으로, 초과하면 오정합점 (outlier)으로 구 분하였다[9]. 여기서 Masuda는 샘플링이 일정하지 않은 무작위 샘플링(random sampling)을 사용한 반면, 본 논문에서는 균일 샘플링 (uniform sampling)을 사용하였다. 한편, Pulli는 점쌍 매칭 단계에서 정적 임계값(hard threshold) 내에서 대응점을 찾되, 각 점 군의 법선 벡터(compatible normal vector)의 사잇각이 45도 이하 이고, 대응점이 메시 경계(mesh boundary) 위에 있지 않는다면 오버랩 영역에 해당하는 동적 임계값(dynamic threshold)을 유지한 채 매칭 대칭(matching symmetric)을 만드는 경험적인(heuristic) 방법을 제안하였다[5]. 그러나 임계값들을 조절하며 많은 시행착오를 거쳐야 하기 때문에 원하는 정합을 얻기까지 오랜 시간이 걸린다는 단점을 안고 있다.
3. 제안하는 방법
본 절에서는 두 점군을 정합할 때에 정확도와 속도를 향상시키는 방법을 제시한다. 이 때, Wu의 방법 [10]을 개선하여 정확도의 향상을 꾀했고 Li의 방법[11]을 참조해 가속화 방법을 개발하였다. 기존의 ICP 방법(그림 2)과 비교할 때, 점 선택(point selection) 단계에서 정확도를 향상시키고 변환(transformation) 단계에서 가속화 기법을 적용하는 것이 본 절의 주된 내용이다.
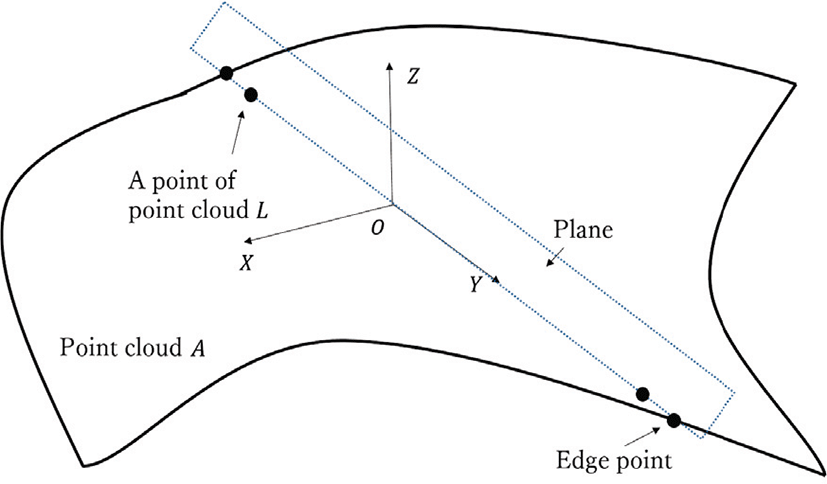
점군 정합은 경계 부분에서 이뤄진다는 Wu의 가정[10]을 사용하여 경계 부분의 점만 샘플링하고 나머지 점들은 제거한다. 이러 한 샘플링 단계에서 필요한 것이 적당한 경계점을 찾는 것이다. 본 논문에서는 경계점을 적절히 결정하는 데 있어서 기존의 방법 [10]과 차이를 두었다. 더불어 2.2절에서처럼, 정합을 하는 데 있어서 정합을 위해 움직이는 점군을 소스 점군 A로, 소스 점군 A의 정합에 최종 목적지가 되는 점군을 타겟 점군 B로 명명한다.
그림 3은 샘플링 과정을 나타낸다. 먼저 점군의 테두리에 있는 경계점을 각도 10도씩의 차이를 주며 36개를 선택한다. 그리고 그림 3와 같이 점군에서 2차 곡면과 각 축의 주성분(principal components)을 계산하고, Y축과 Z축로 이루어진 YZ평면을 만든 다. 그리고 아래의 순서를 통해 점군 L을 이루는 점을 선택한다.
-
평면 위에 놓이는 소스 점군 A의 점들을 Y축 기준으로 양의 방향과 음의 방향으로 나는다.
-
만약 Y축 기준으로 양의 방향에 점의 개수가 n이라면, 원점 O로부터 0.9n번째 멀리 떨어진 점을 선택한다. 예를 들어, n이 1,000이라면 900번째 멀리 떨어진 점을 선택한다.
-
Y축 기준으로 음의 방향에서도 2)의 과정을 반복 한다.
-
Z축을 기준으로 각도를 10도 회 전한다.
-
위 1)-4)를 17번 반복한다.
-
선택된 모든 점을 점군 L에 포함시킨다.
Wu는 0.9D 거리에 있는 점을 적당한 경계점으로 선택했는데, 이 때 D는 원점 O에서 최대 경계까지의 거리이다[10]. 하지만 실제로 스캔한 물체 주변의 배경에는 노이즈가 존재한다. 이런 상황에서\ Wu의 방법을 사용한다면 0.9D 거리에 있는 점은 스캔한 물체의 경계점이 아니라 배경의 노이즈일 확률이 높다. 그러나 노이즈 필터링을 통해 배경의 노이즈를 제거하고 난 뒤 0.9D 대신에 0.9n을 이용한다면 점들의 밀도가 높은 부분, 즉 스캔한 물체의 점군 안에서 적당한 경계점을 선택하게 된다. 그러므로 본 논문 에서는 0.9n 번째에 해당하는 36개의 점들로 점군 L을 구성하였다. 한편, 타갯 점군 B의 오버랩 부분을 모르므로, 균일 샘플링 (uniform sampling)을 수행한 결과로 점군 U을 구성하였다.
위와 같이, 소스 점군 A로부터 찾은 경계 점군 L과, 타갯 점군 B로부터 균일 샘플링된 점군 U를 구성한 뒤에는, 곡률을 이용하여 오버랩을 찾는다. 먼저 가우시안 곡률(Gaussian curvature, K) 과 평균 곡률(mean curvature, H)을 계산한다. 그리고 표 1의 분류를 이용하여 서로 다른 종류를 가진 점의 쌍을 제거한다. 이 때, 오버랩을 찾는 데에 악영향을 끼치는 평판 요소도 제거한다.
| K < 0 | K = 0 | K > 0 | |
|---|---|---|---|
| H < 0 | Hyperbolic concave | Cylindrical concave | Elliptical concave |
| H = 0 | Hyperbolic symmetric | Planar | – |
| H > 0 | Hyperbolic convex | Cylindrical convex | Elliptical convex |
L과 U에서 남은 점을 각각 p, q라 명명하고, 아래의 식을 만족하지 못하는 (p, q) 쌍을 제거한다.
이때, ϵ1, ϵ2은 곡률 임계값(curvature threshold)이다.
마지막으로, 남은 점군 쌍에 zncc(zero mean normalized cross correlation) 방법을 활용하여 이웃한 점 들의 곡률 매칭 (neighborhood curvature matching)을 수행한다[13].
zncc는 포괄적인 이웃 곡률 매칭 지수(comprehensive neighborhood curvature matching degree)이고,과 은 k-최근접 이웃 알고리즘(k-nearest neighbor search, k-NN) 으로 얻은 이웃점의 주곡률(principal curvature) 평균이다. 방정식 (1)과 방정식 (2)를 적용한 이후 쌍이 없는 점군 L의 점은 zncc를 0으로 놓는다. 점군 L의 각각의 점에 대해 zncc가 가장 높은 점의 쌍을 선택한다.
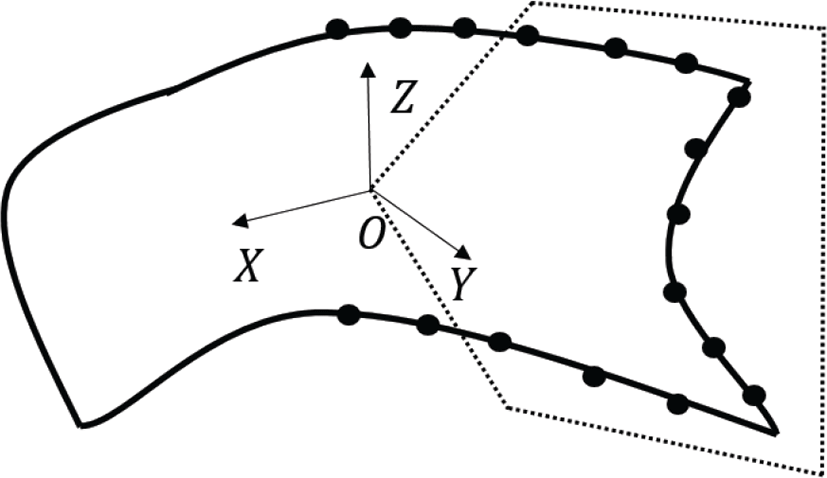
zncc는 오버랩 영역을 찾는데 사용된다. zncc의 값이 1보다 큰 점쌍의 개수를 묶는 사슬을 만든다. 그리고 그림 4와 같이 사슬을 구성하는 점 zncc 합이 가장 큰 사슬을 이용하여 O-XYZ 공간을 만들고 O와 사슬을 이어 오버랩 영역을 찾는다. 소스 점군 A의 이러한 오버랩 영역을 소스 오버랩 점군 A′ 으로 명명한다. 이 과정을 타갯 점군 B에도 적용하여 타갯 오버랩 점군 B′을 결정 한다.
Li의 가속화 방법[11]은 낮은 오버랩의 상황에서는 활용할 수 없다. 하지만 앞서 진행한 샘플링 기법을 적용하면 90% 이상으로 오버랩이 증가하게 된다. 그래서 본 논문의 가속화 기법은 낮은 오버랩에서도 적용할 수 있는 범용성을 가진다. 가속화를 적용하는 순서는 다음과 같다.
-
1) 회전행렬 Rj,i과 병진벡터 Tj,i를 소스 오버랩 점군 A′에 적용한다.
-
2) δR과 δT를 다시 적용한다.
-
3-1) 만약 오차가 줄어들면 2)를 다시 적용한다.
-
3-2) 만약 오차가 늘어나면 소스 오버랩 점군 A′를 δR, δT을 적용하기 전으로 옮기고 점쌍을 찾는 단계(point pair matching step)으로 돌아간다.
위 과정을 dj,i − dj+1,i < τ 이 만족될 때까지 반복한다. dj,i는 j번 반복했을 때의 소스 점군 A와 타갯 점군 B 간의 제곱평균 제곱근 오차(RMSE)이며 τ는 한계치 (tolerance)이다. 위 과정에서 회전행렬 Rj,i과 병진행렬 Tj,i는 점대평면(point-to-plane)을 기반으로 구하되[7], 사원수(quaternion)를 이용하예[8] 회전행렬 Rj,i을 구한 다음에 병진행렬 Tj,i사를 구하였다. 회전행렬 Rj,i과 병진행렬 Tj,i사를 구하는 식은 다음과 같다[8].
이 때, q0, qx, qy, qz는 사원수 에 대한 실수부 (real part) 와 허수부 (imaginary part) 이다. 또, 와 는 각각 소스 오버랩 점군 A′과 타켓 오버랩 점군 B′를 구성하는 점들의 평균 좌표값이며, 이는 각 점군의 중심 (centroid)을 의미한다.
한편, δR과 δT는, j번째 회전 및 병진 행렬인 Rj,i과 Tj,i를 적용 하여 단 한 번의 반복횟수(iteration)로 오버랩 점군 A′을 이동시킨 뒤에 그 자리에서 다시 구한 회전 및 병진 행렬로써, (j+1)번째 반복횟수의 회전 및 병진 행렬인 Rj+1,i 및 Tj+1,i과는 다르다.
4. 실험 결과
본 논문에서는 정합 분야에서 흔히 사용되는 3차원 점군 데이터 인 스탠포드 토끼 (Stanford bunny), 불상(buddha), 아르마딜로(armadillo)를 테스트 점군으로 사용하였는데, 데이터에는 노이즈가 포함되어 있다. 원래의 샘플링 방법은 일반적인 노이즈 환경에 적용되지 않기 때문에 비교 대상이 되는 타갯 점군으로는 실제 데이터를 사용한 것이고, 이 때 점군 데이터의 오버랩은 약 30〜40% 이다. 위 세 가지 점군 데이터는 초기 정합을 충분히 적용한 상태이다. 본 논문에서 적용한 균일 샘플링(uniform sampling)은 1/5 이며 곡률 임계값(curvature threshold)는 0.2로 설정하였다. 그리고 본 논문에서 정합 결과를 평가하는 지표 중의 하나인, j번째 반복횟수(iteration)의 제곱평균제곱근 오차(RMSE)는 다음과 같이 구한다.
즉, 소스 점군 A에 대응하는 점을 타갯 점군 B로부터 추출하고 이를 Y라고 하면, 점군 A와 점군 Y의 유클리드 거리(Euclidiean distance, d)를 제곱하여 모두 더하고 소스 점군 A의 점 개수 ma 만큼 나누어 제곱근한 것이다.
샘플링 기법을 적용하지 않은 채(not-sampled) 정합을 수행한 결과는 다음과 같다. 표 2를 보면, 소스 점군의 점 개수는 노이즈를 포함하여 36,726개이며, 타겟 점군의 점 개수는 노이즈를 포함 하여 20,657개이다. 이 때, 전체 계산 시간은 12.04초이다. 그림 5는 위 결과를 가시적으로 나타낸 것이다. 소스 점군 A(파랑)를 타겟 점군 B(빨강)에 정합하기 전(그림 5a)과 정합한 후(그림 5b)의 모습을 비교할 수 있다. 이때, 그림 5b의 검정 원 부분을 그림 5c에서 살펴보면 토끼 꼬리 부분이 제대로 정합되지 않은 것을 확인할 수 있다.
| Source point cloud A (Blue) | Target point cloud B (Red) | |
|---|---|---|
| not-sampled | 36,726 | 20,657 |
| sampled | 17,102 | 11,044 |
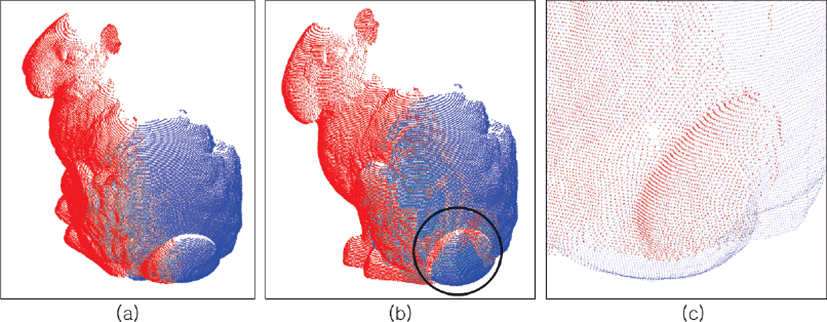
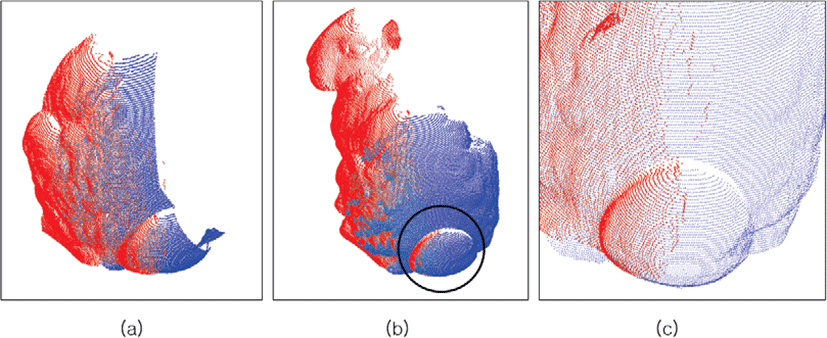
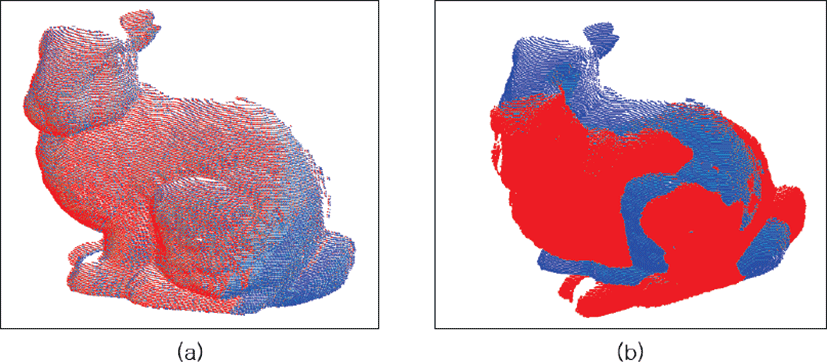
샘플링 기법을 적용한 채 (sampled) 정합을 수행한 결과는 다음과 같다. 샘플링된 소스 점군의 점 개수는 표 2에 나타낸 바와 같이 노이즈를 포함하여 17,102개이며, 샘플링된 타겟 점군의 점 개수는 11,044개이다. 샘플링 시간은 0.479초이고 정합시간은 1.11 초이다. 그림 6은 소스 오버랩 점군 A′(파랑)이 타겟 오버랩 점군 B′(빨강)을 기준으로 정합하기 전(그림 6a)과 정합한 후(그림 6b)를 비교한 것 이 다. 그림 6b의 검 정 원 부분을 확대하여 살펴보면, 그림 5c와 달리 그림 6c에서 토끼 꼬리가 잘 정합된 것을 알 수 있다. 한편, 타겟 점군 B를 향해 소스 점군 A가 정확하게 정합되어 제곱평균 제곱근 오차가 0일 때의 레퍼런스(reference) 소스 점군 A″(빨강)를 기준으로, 본 논문의 샘플링 기법을 적용하여 정합한 그림 해의 소스 점군 A(파랑)를 그림 7a에 나타내었으며, 샘플링 기법을 적용하지 않고 정합한 그림 5b의 소스 점군 A(파랑)를 그림 7b에 나타내었다. 후자의 경우보다는 전자의 경우에서 소스 점군 A가 이상적인 위치(빨강)에 가까운 것을 그림 7에서 보여 줌으로써, 샘플링을 적용한 정합의 결과는유효하다고 판단할수 있다. 더불어, 오버랩되는 점들을 찾는 샘플링 기법을 사용하여 이 점들로만 정합하는 것이 그렇게 하지 않은 정합보다 반복횟수 가 1/5 수준으로 감소하고 시간도 1/10로 줄어들었을 뿐만 아니라 오차도 약 1/9로 감소한 것을 표 3에서 확인할 수 있다.
| w/o overlap region | w/ overlap region | |
|---|---|---|
| Iteration [no.] | 173 | 37 |
| Time [sec] | 12.04 | 1.11 |
| RMSE [mm] | 0.008241 | 0.000898 |
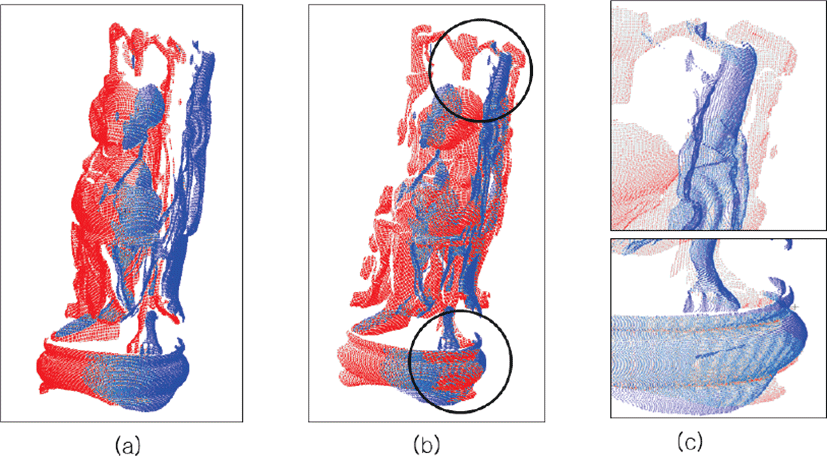
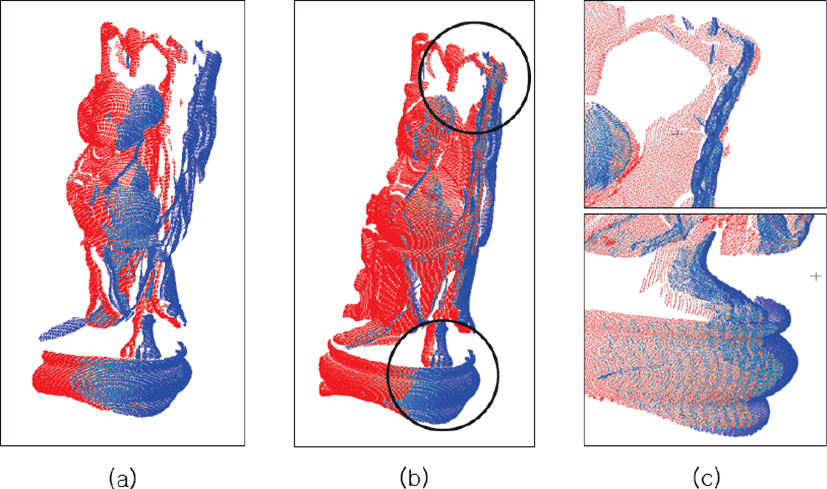
샘플링 기법을 적용하지 않은 채(not-sampled) 정합을 수행한 결과는 다음과 같다. 그림 8에 나타난 소스 점군의 점 개수는 노이즈를 포함하여 78,056개이며, 타겟 점군의 점 개수는 노이즈를 포함하여 61,872개라는 것을 표 4에서도 확인할 수 있다. 그리고 전체 계산 시간은 36.3초이다. 그림 8은 위 정합 결과를 시각적으로 나타낸 것이다. 소스 점군 A(파랑)를 타겟 점군 B(빨강)에 정합하기 전(그림 8a)과 정합한 후(그림 8b)의 모습을 비교할 수 있다. 여기서 그림 8b에 검정 원을 표시한 것처럼, 그림 8c에서 자세히 살펴보면 부처의 팔과 발, 발판이 정합되지 않은 것을 알 수 있다.
| Source point cloud A (Blue) | Target point cloud B (Red) | |
|---|---|---|
| not-sampled | 78,056 | 61,872 |
| sampled | 56,412 | 52,361 |
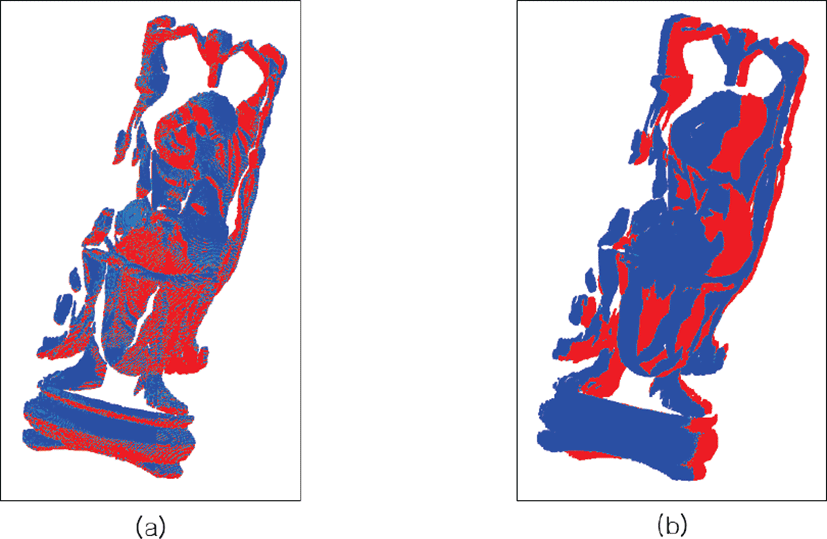
샘플링 기법을 적용한 채 (sampled) 정합을 수행한 결과는 다음과 같다. 표 4에서처럼, 샘플링된 소스 점군의 점 개수는 노이즈를 포함하여 56,412개이며, 샘플링된 타갯 점군의 점 개수는 52,361 개 이다. 샘플링 시간은 1.144초이고 정합 시간은 7.31 초이다. 그림 9는 불상 점군의 소스 오버랩 점군 A′파랑)이 타갯 오버랩 점군 B′(빨강)을 기준으로 정합하기 전(그림 9a)과 정합한 후(그림 9b)를 비교하여 나타낸 것이다. 그림 8b에서 정합에 실패하 였던 부분이 그림 9b에서는 잘 정합된 것을 확인할 수 있다. 이 점군에서도, 샘플링 기법을 적용하여 정합한 소스 점군 A(파랑)과 그렇지 않은 소스 점군 A(파랑)를 레퍼런스(reference) 소스 점군 A″(빨강)과 대비하여 각각 그림 10a와 그림 10b에 제시하였으며, 그림 10c를 통해 샘플링 기을 적용한 정합이 우수하다고 판단 내릴 수 있다. 불 점군 정합에서는 반복횟수는 1/3, 시간은 1/5, 오차도 무려 1/15 로 감소하였음을 표 5에 나타내었다.
| w/o overlap region | w/ overlap region | |
|---|---|---|
| Iteration [no.] | 121 | 43 |
| Time [sec] | 36.3 | 7.31 |
| RMSE [mm] | 0.003326 | 0.000221 |
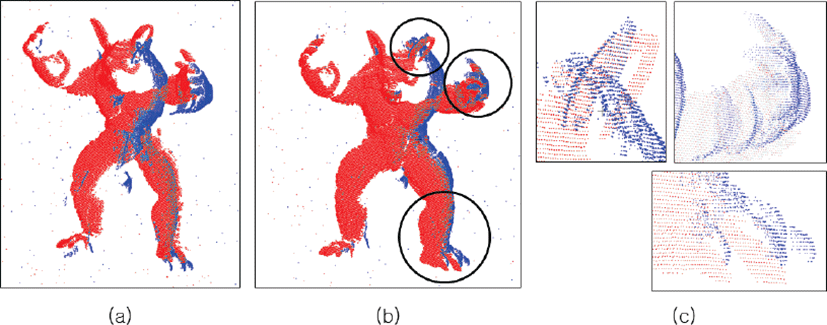
샘플링 기법을 적용하지 않은 채(not-sampled) 정합을 수행한 결과는 다음과 같다. 그림 11에 나타난 소스 점군의 점 개수는 노이즈를 포함하여 27,875개 이고, 타갯 점군의 점 개수는 노이즈 포함 20,100개로, 표 6 에 나타내었다. 전체 계산 시간은 4.13초이며, 아르마딜로 소스 점군 A(파랑)를 타갯 점군 B(빨강)에 정합하기 전(그림 11a)과 정합한 후(그림 11b)의 모습을 살펴보면 아르마딜로의 손, 발, 귀가 서로 각각 정합되지 않음을 그림 11c 에서 확인할 수 있다.
| Source point cloud A (Blue) | Target point cloud B (Red) | |
|---|---|---|
| not-sampled | 27,875 | 20,100 |
| sampled | 13,316 | 11,803 |
샘플링 기법을 적용한 채(sampled) 정합을 수행한 결과는 다음과 같다. 표 6 에서처 럼, 샘플링된 소스 점군의 점 개수는 13,316 개이고, 샘플링된 타갯 점군의 점 개수는 11,803개이다. 샘플링 시간은 0.459초이며 정합 시간은 4.12초이다.
그림 12는 소스 오버랩 점군 A′파랑)이 타갯 오버랩 점군 B′(빨강)을 기준으로 정합하기 전(그림 12a)과 정합한 후(그림 12b)를 비교한 것이다. 그림 11b에서 정합에 실패하였던 아르마 딜로의 손, 발, 귀가 그림 12b에서는 제대로 정합된 것을그림 12c 에서 관찰할 수 있다. 그림 13a와 그림 13b는 샘플링 기법을 적용하여 정합한 소스 점군 A(파랑)과 그렇지 않은 소스 점군 A(파랑)를 레퍼런스(reference) 소스 점군 A″(빨강)과 대비하여 나타낸 것이며, 아르마딜로 점군에서도 샘플링 기법은 유효함을 제시할 수 있다. 다만, 반복횟수는 오히려 1.7배 정도로 증가하고 시간도 큰 변화가 없을지 라도 오차는 1/5배로 감소하였으므로 정확도 측면에서 향상되었음을 표 7에서 볼 수 있다.
| w/o overlap region | w/ overlap region | |
|---|---|---|
| Iteration [no.] | 59 | 103 |
| Time [sec] | 4.13 | 4.12 |
| RMSE [mm] | 0.002683 | 0.000573 |

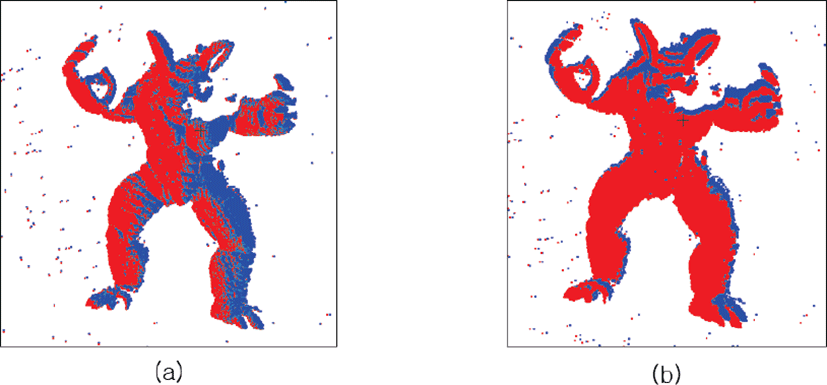
앞서 사용한 세가지 점군 데이터를 가지고 가속을 적용하기 적용하기 전과 후를 비교하였다. 모든 경우에 대하여 제곱평균제곱근 오차(RMSE)는 거의 변하지 않았지만 반복횟수가 많이 줄어 들었다. 표 5 에 따르면, 기존보다 토끼는 1/3배, 부처는 1/2배, 아르마 딜로는 1/5배로 줄어든 것을 확인할 수 있다.
제곱평균제곱근 오차(RMSE)의 값이 커보이지만, 이 오차는 레퍼런스(reference)에 대한 오차가 아니라, 오차를 계산하는 과정에서 노이즈와의 오차가 포함되었기에 이러한 결과가 나온 것 이다. 레퍼런스와 비교해도 위 점군 데이터들은 정합이 잘 된 것이고, 시각적으로도 확인할 수 있다.
5. 결론
ICP 알고리즘은 점 개수가 많은 점군 데이터의 정합에 효과적이다. 다만 ICP 알고리즘이 점들의 위치를 변화시키지 않기 때문에 연식(non-rigid) 정합에는 적합하지 않을지라도, 플랜트나 조선 등 다루는 구조물이 크고 복잡한 산업 현장에는 매우 효과적임은 단언할 수 있다. 이러한 상황에서는 스캔한 점군의 점 개수가 매우 많기 때문에 샘플링과 가속화가 필수적이다. 하지만 본 논문의 샘플링 알고리즘에는 평면을 제거하는 단계가 있기 때문에 평면을 가진 구조물에는 적용할 수 없다는 단점을 안고 있다. 이 단점을 극복하기 위해서는 평면을 포함하면서도 불필요한 점쌍을 정확히 찾는 알고리즘을 추가해야 한다. 그리고 본 논문의 가속 알고리즘이 간단하고 강력할지라도 정확도가 다소 떨어진다는 단점이 있다. 그래서 정확도 감소를 최소화하도록 본 논문의 알고리즘을 더 발전시켜야 한다.