1. Introduction
In computer graphics research, cloth simulation has been studied for a long time. There were many topics about cloth simulations like the motions of cloth, collision detection with other objects or acceleration of a simulation. However, most cloth simulations have studied dry cloth. The study of wet cloth was less studied than a study of dry cloth.
The wet cloth has various characteristics than a dry cloth. When a dry cloth gets wet, it adheres to the body and makes more wrinkles. Many studies have investigated simulations of wet cloth that has different characteristics than dry cloth. Most wet cloth simulations have used the fluid-cloth two-way coupling method considering both fluid and cloth simulations. The first two-way coupling method proposed did not consider the diffusion of the fluid throughout the cloth [5]. Afterwards, one study [6] proposed the two-way coupling method of a porous object and cloth, and another [7] proposed a method in relation to how fluid diffuses in cloth. Until recently, research on wet cloth has proposed a two-way coupling method considering both fluid and cloth simulations [8]. These studies have proposed a method of diffusion focusing on fluid simulation; however, they have not discussed the motion of wet cloth on the surface of an object.
Unlike previous researches, several studies have proposed various methods to simulate wet cloth without considering fluid particles. By using the feature that many wrinkles are created when cloth gets wet, [10] proposed a novel buckling method that produced numerous wrinkles in the cloth of a virtual avatar that looked similar to those in wet cloth. They simulated the wet cloth without considering the additional force of fluid, but considered a simplified mass saturation model that computes the mass of the cloth when it gets wet and a skin-to-cloth friction model based on real-world experiments. [12] aslo simulated the wet cloth without considering fluid particle and showed the varying motions of wet cloth under different humidity environments by using the adhesion force model based on real-world experiments in textile research.
Similar to the presented works, we simulate the wet cloth without considering fluid simulation. If we consider both fluid and cloth simulations, the simulation will be complex and time-consuming because we need to compute some values about not only cloth vertices but also fluid particles and consider exchanging physical quantities between fluid particles and cloth vertices. Because one of our purpose is that showing more realistic result than previous works through easier method, we do not consider fluid particles simulation in our experiments. As we do not consider fluid particles, we must compute the force that fluid gives to cloth. Thus, we use the adhesion force that has been modeled in textile research based on real-world experiments and show the phenomenon that wet cloth sticks to a surface of an object. In previous work [12], they used this adhesion force model to express the wet cloth and computed the force based on the area of the cloth contacting the surface of an object. They could express the adhesive phenomenon of wet cloth by using adhesion force model, but there were some artifacts that part of the wet cloth contacting the surface of an object totally adhered to the floor because the contacting area had same adhesion force. Differing from their work, we compute the adhesion force based on the vertex of the cloth, so each cloth vertex can have different adhesion force values. Through this, we produce natural wrinkles in the part of the cloth contacting the surface of an object. Furthermore, by expressing object-cloth adhesion effects and cloth-cloth adhesion effects that occur when the cloth collides with itself, we show more realistic results of the collisions of a wet cloth.
2. Related work
Cloth simulation has been studied for a long time in computer graphics research. Based on the elastic theory, [1] primally expressed time-varying cloth dynamics. In addition, [2] proposed a mass-spring cloth model that is widely used as the basic structure of cloth. They modeled the cloth structure as vertices that have a mass and spring that join two vertices, controlled the tension and the damping of the springs by an internal force, and limited the length of the springs to be shorter and longer than a certain length using a distance constraint. To resolve the problem in previous works that used a small time step to ensure the numerical stability of simulation, [3] used an implicit integration method that allowed them to use a large time step and maintain simulation stability. [4] resolved the post-buckling problem that was not resolved by the implicit method by using the semi-implicit method.
We use the mass-spring model previously introduced for modelling the basic structure and dynamics of cloth and compute the position and the velocity of vertices in the next time step by the semi-implicit Euler integration method.
Studies of wet cloth simulation only began relatively recently. Wetting cloth by fluid is the same as the cloth interacting with fluid, so most studies with simulations of the wet cloth consider both fluid and cloth simulations. [5] proposed a two-way coupling method for interactions between fluid and a shell using a smoothed particle hydrodynamics (SPH) method that formulates the fluid dynamics, but there was a limit in that the fluid could not pass through the shell. Unlike previous works, [6] proposed the porous object-fluid interaction method using Darcy’s law and showed how a fluid flows out of a porous object such as cloth using fluid simulation. [7] extended the previous two-way coupling method by using the fluid diffusion model obtained from Fick’s laws of diffusion and proposed a novel two-way coupling method focusing on how a fluid diffuses in a cloth. Similar to these works, wet cloth simulation that considers both fluid and cloth simulation has been recently studied [8]; however, because that study focused on the interaction between fluid and cloth, the motion of the wet cloth when lying on the surface of the object was not investigated.
Some studies proposing a method to simulate the collisions of wet cloth have not considered the fluid particle used in fluid simulation. [9] used fractional derivatives to study the collisions of cloth underwater without considering fluid simulation. Using the feature that cloth gains more wrinkles when wet, [10] proposed a novel buckling method that added many wrinkles to show that wet cloth appears with wrinkles in a similar manner as real-world wet cloth. However, when cloth gets wet in the real-world, it tends to adhere to the surfaces of objects because of the fluid between the cloth and the surface of the object it contacts. They did not consider this feature and simply expressed that the wet cloth had more wrinkles, so they could not express the adhesive phenomenon that the cloth adheres to the surface of objects. [11] thought that a cause of the adhesive phenomenon is the difference in pressure between the closed space by wet cloth and the atmosphere, so they attempted to show that the adhesive phenomenon causes the wet cloth to stick to the surface of the object. However, the result of applying this difference in pressure showed a sharp and concave tent-shape when pulling up the center of the cloth on the table rather than the adhesive phenomenon of wet cloth. [12] considered using the adhesion force model based on real-world experiments in textile research to express wet cloth adhering to the surface of an object and showed various motions of the wet cloth according to different humidity environments. They showed the adhesive phenomenon of the wet cloth sticking to the surface of the object, but part of the cloth that was sticking to the surface of the object adhered to the floor entirely. In addition, [13] introduced a method by using rendering without any additional force to make the cloth appear wet.
Similar to these previous works, we express wet cloth without a fluid simulation. To do so, we use the adhesion force model that is theoretically modeled in textile research based on real-world experiments. Although previous work[12] has also used this adhesion force model, our study differs in terms of the application of the adhesion force and the production of natural wrinkles in the part of the cloth sticking to the surface of the object. Moreover, we show the phenomena where the wet cloth adheres to the surface of an object, and to itself when undergoing self-collision.
3. Algorithm
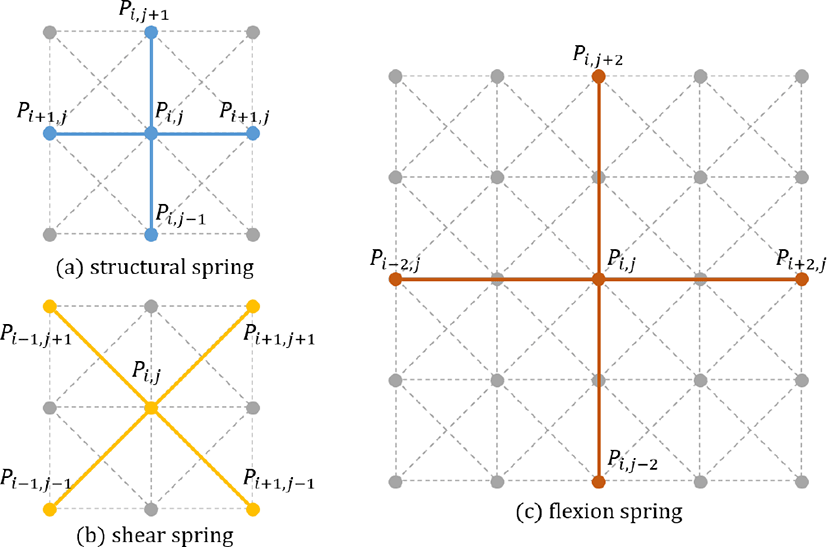
We use the mass-spring model of the cloth proposed by [2] to express the basic dynamics of the cloth. We make the structure of the cloth by composing m × n vertices that have mass and massless springs that join two adjacent vertices. Springs connecting P(i, j) and P(i+1, j), P(i−1, j), P(i, j+1), or P(i, j − 1) are called structural springs, springs connecting P(i, j) and P(i + 1, j + 1), P(i + 1, j − 1), P(i − 1, j + 1), or P(i + 1, j − 1)) are called shear springs, and springs connecting P(i, j) and P(i+2, j), P(i−2, j), P(i, j+2), or P(i, j−2) are called flexion springs, see [Figure 1]. Structural springs express the expanding and contracting of the cloth, shear springs express the shear stress of the cloth, and flexion springs express the bending stress of the cloth. The internal force of the springs consists of tension and damping terms, so the force is computed as Eq. (1).
where j is an index of vertices that are linked with Pi by a spring. kstiffness and kdmaping are constants of stiffness and spring damping, Iij is a position difference vector between two vertices, Pi and Pj, i.e., Iij = Pj − Pi, lij, and are the current and initial lengths of two linked vertices, and vij is the velocity difference between two linked vertices.
We use the friction model based on Coulomb’s friction model about both static and kinetic friction proposed by [15]. He proposed the velocity control method to express the friction model, and because the friction force acts to oppose the direction of motion of an object and is parallel to the contacting surface, they only controlled the tangential velocity, vT, of the cloth. The friction force is in the opposite direction as the pre-friction tangential velocity, . If the friction velocity vf is larger than , then the cloth maintains its static state because of the static friction force or will stop because of the kinetic friction force. In other words, the tangential velocity vT will be 0 in this state. We can obtain the final tangential velocity as follows.
When a cloth is wet due to fluid, its whole mass increases. To show this feature, we apply the mass saturation model based on real-world experiments proposed by [16], which derives the equation of the amount of fluid absorbed by the cloth over time.
where A(g) is the amount of fluid absorbed by the cloth at time t(min), B is weight constant in the saturated state per 1 g, and c is the hygroscopicity constant depending on the cloth material. This equation calculates the amount of the fluid absorbed by the cloth at time t. The variation in the amount of the fluid absorbed by the cloth in a time step also needs to be calculated, so we compute this variation and apply it to the mass of the cloth in the next time step.
where B and c use values obtained from real-world experiments.
| Cotton | Course wool | High absorption fabric | |
|---|---|---|---|
| B | 0.84 | 1.24 | 2.492 |
| c | 8.884 | 4.8936 | 3.3803 |
The wet cloth tends to adhere to the surface of the object when the cloth contacts with the object because having fluid between the cloth and the object produces an adhesion force. When the cloth gets wet, the fluid makes a liquid bridge and an adhesion force. The force from the pressure difference between the liquid bridge and the atmosphere and that from the surface tension of the liquid bridge include the adhesion force that allows the wet cloth to adhere to the surface of the object.
[14] modeled the liquid bridge (see [Figrue 2]) and proposed a theoretical adhesion force model based on two causes of adhesion force. We express the adhesive phenomenon between the cloth and the surface of the object using this adhesion force model to obtain the adhesion force as follows.
where γ is the surface tension constant of the fluid that makes the liquid bridge, r is the radius of the circle that supposes that the contact surface between the cloth and the liquid bridge is a circle, h is the height of the liquid bridge, θa and θb are contact angles where the liquid bridge meets the cloth and contact surface, and R1 and R2 are the principal radii of curvature of the liquid bridge and the atmosphere. One of the causes of adhesion force is by a pressure difference between the air (atmosphere) and the fluid which makes the liquid bridge and the other is by a surface tension of the fluid. First term of the right side of Eq. (5) means the force made by a pressure difference between the air and the fluid which is computed according to Young-Laplace equation, and second term means the force made by the surface tension of the fluid.
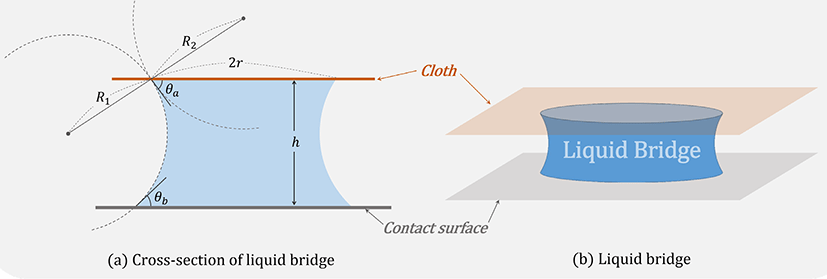
We use a surface tension constant of water as γ to express the wet cloth by water. If the positions of the vertices of the cloth model used in the experiments are regular, we suppose that r is half of the interval of two vertices. For example, if the interval of two vertices is 1 cm, then we compute the adhesion force with r as 0.5 cm. A liquid bridge has a non-zero small height when the cloth totally adhered to the contact surface and is destroyed when the distance between the cloth and the contact surface is longer than the maximum height of the liquid bridge we defined. As the height of the liquid bridge increases, the principal radii of curvature R1 and R2 will also be increased, thereby increasing the contact angles, θa and θb. So we defined the values of contact angles as 90 when the liquid bridge has its maximum height and as non-zero small value like 0.001 when the cloth totally adhere to the contact surface.
The adhesion force appears not on the whole part of the cloth, but rather on the part of the cloth that contacts the object. Considering this feature, previous work [12] modified the adhesion force model and computed the force based on the area where the wet cloth contacts the object. They compute the area where the cloth adheres to the contact surface, then compute the adhesion force using this area, so the area is computed only once in a time step. If the adhesion force is computed only once in a time step and is applied to the whole cloth, it is contrary to the definition of adhesion force because the adhesion force appears when part of the wet cloth contacts the object. Even if the adhesion force is applied to only the contacting area part, the wet cloth cannot make natural wrinkles because the contacting part has the same adhesion force distributed throughout its surface.
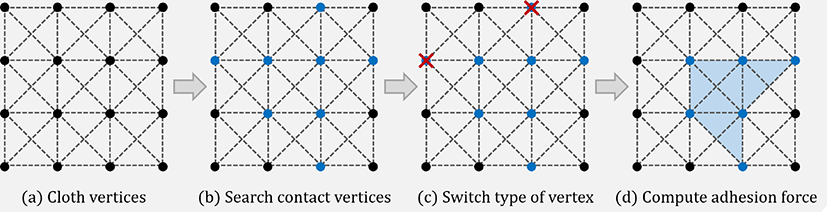
To solve this problem, we compute the adhesion force based on each vertex rather than the area of the cloth that contacts the object. First, we find the vertices that contact with the object and define them to the type of contact vertex(blue vertices in [Figure 3]). Among these contact vertices, if there are vertices where the distance from the vertex to the surface of the object contacted by the vertex is longer than the predefined maximum distance (height) of the liquid bridge, then we switch the type of these vertices to non-contact vertex(black vertices in [Figure 3]). Lastly, we supposed that the vertices where the distance from the vertex to the surface of the object that the vertex contacted is longer than the predefined maximum distance (height) of the liquid bridge have a liquid bridge, and the adhesion forces about these vertices were calculated. Through our method, each contact vertex can have different height of the liquid bridge, and, unlike previous work, each part of the area of the cloth that contacts the object can have different values of adhesion force. As a result, we can create natural wrinkles in the area of the cloth contacts the object or the floor.
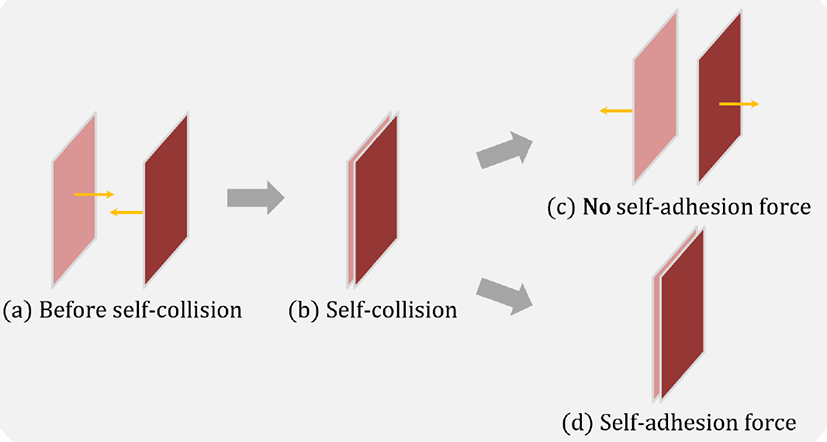
In the real world, similar to the adhesion force between the cloth and the surface of the object that appears when the cloth and object collide, the adhesion force also appears when the cloth collides with itself. When the cloth collides with itself, i.e., self-collision occurs, a liquid bridge is made between the cloth and the cloth; this bridge makes the adhesion force. [10] proposed a buckling method that makes many wrinkles in the wet cloth appear similar to wrinkles of real-world wet cloth. Because this work did not consider the force that the fluid imposes onto the cloth, they did not show the adhesive phenomenon of the wet cloth. Thus, neither the adhesive phenomenon of the cloth adhering to the skin of the virtual avatar nor the adhesive phenomenon of the cloth adhering to itself (called self-adhesion effect) were expressed.
[12] introduced the concept of humidity, which was not mentioned in previous studies, and based on this, showed various motions of the wet cloth. In this work, they used the adhesion force to express the phenomenon of the cloth adhering to the surface of the object, but they did not address the self-adhesion effect. Instead, they simply constrained the distance between two vertices so that they would not get too close.
We used the adhesion force model that is theoretically modeled to express the adhesive phenomenon between the cloth and the surface of the object. In the same manner, we applied the adhesion force between the cloth and itself, which demonstrated a force that is observed to affect wet cloth in the real world. If there is only the cloth-object adhesion force, the wet cloth progresses to the flat position because of gravity, which acts similar to the dry cloth. However, if there is a self-adhesion force, the result of the wet cloth is different from the result of dry cloth and is more similar to the experimental results observed for wet cloth. See [Figure 4].
We proposed a method of computing the adhesion force based on vertices. A previous study [12] also used the adhesion force model and determined the adhesion force due to the cloth adhering to the surface of the object. However, they computed the adhesion force based on the area where the cloth contacts the object and computed the adhesion force only once in a time step. Consequently, all vertices in the area of the wet cloth contacting the surface of the object had the same values of adhesion force, and as a result, part of the wet cloth is adhered to the surface of an object without wrinkles.
We search the vertices that contact the object and define these vertices as the type of contact vertex, and then we compute the adhesion force supposing that each vertex has a liquid bridge. Therefore, the contact vertices can have differing liquid bridge heights and contact angles, so they also can have differing adhesion force values. By computing the adhesion force based on the vertices, we can model the natural wrinkles in the wet cloth at the contacting area that were not expressed in previous studies.
4. Experiment
We experimented with an Intel Core i7 7700 K desktop computer with 16 GB RAM and simulated the wet cloth interactions through C++ programming using the OpenGL library. We conducted various experiments to express the features of the wet cloth interactions. In the adhesion force used to express the adhesive phenomenon, the maximum height of the liquid bridge was defined as 0.1 cm. If the cloth model had the regular spacing of all vertices, we defined the spacing of two vertices as 1 cm and the radius of the liquid bridge r as 0.5 cm, or half of the spacing of two vertices.
We defined the contact angles θa and θb as non-zero small values when the liquid bridge had the maximum height and as 90 when it had the minimum height. To simulate cloth wetted by water, we defined the surface tension constant γ of water for computing adhesion force as 75.75, and to simulate cotton cloth, we defined the weight constant B as 0.84 and the hygroscopicity constant c as 8.884 for computing variations in the mass of the cloth.
| Figure # | Resolution of cloth | # of point | Total mass (g) | Scaling factor of adhesion force |
|---|---|---|---|---|
| Figure 5 | 60 × 60 | 3,600 | 662 | 2 |
| Figure 6 | - | 3,077 | 566 | 3 |
| Figure 7 | 50 × 50 | 2,500 | 460 | 1.5 |
| Figure 8 | 40 × 40 | 1,600 | 294 | 1 |
| Figure 9 | 20 × 20 | 800 | 147 | 1 |
We used the theoretical adhesion force model based on real experiments in textile research. Differing from the previous work that computed the adhesion force based on area, we computed the adhesion force based on the vertex so that the vertices contacting the object had different adhesion force values. [Figure 5] shows the result of a wet cloth dropping on a static ball. In previous work, the adhesion force was computed only once per time step, so all vertices in the area of the cloth contacting the object had the same adhesion force. As a result, this area was completely adhered to the floor. We then computed the adhesion force based on the vertex. The results show that the vertices in the area of the cloth contacting the object have different liquid bridge heights and adhesion forces. Through this method, we could express the realistic wrinkles that were not expressed in the previous work in the area where the cloth contacts the floor.

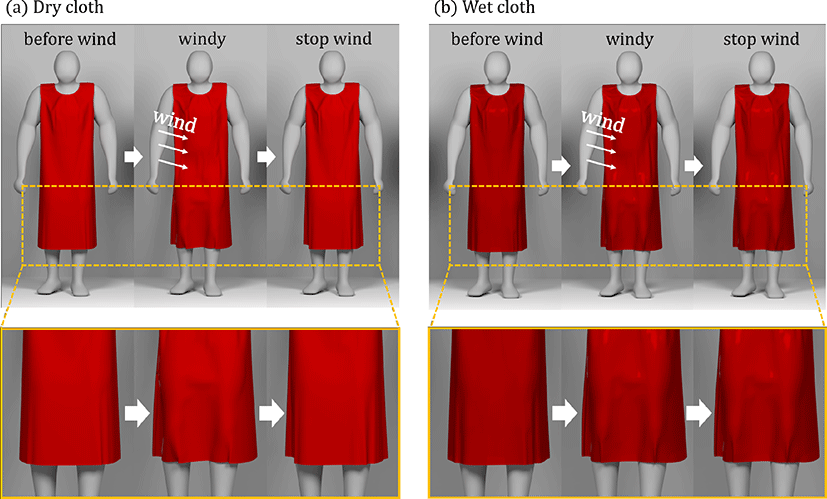
Previous work [10] has proposed a novel buckling method to the wet cloth that explains why many wrinkles are made when moving. However, their whole method did not consider the force from the fluid, so the wet cloth in the result having the same motion as the dry cloth. [Figure 6] is the result of starting and stopping the wind of with same size and same direction as the dressed avatar. Dry cloth returns to the position before the wind blows because there is no force to adhere it to the avatar, but wet cloth adheres to the skin of the avatar just like the real-world wet cloth, even after the wind stops, because of the adhesion force.
The wet cloth is heavier than the dry cloth because the wet cloth contains fluid. Thus, when dropping the cloth on a ball, the wet cloth sagged more than the same cloth when it was dry; see [Figure 7(a)]. The adhesion force of the wet cloth exists in the areas of contact with the floor and ball, so when the ball is rotated, the wet cloth tends to adhere more to the ball than to the dry cloth. When these balls are rotated at the same time, the wet cloth has more wrinkles than the dry cloth because of the increased adhesion force between the wet cloth and both the ball and the floor [Figure 7(b)].

More force was needed when moving the wet compared with the dry cloth. This is because the wet cloth tends to adhere to the floor as a result of the liquid bridge between the cloth and the floor that makes the adhesion force. [Figure 8] shows the result of applying the same 4000 N vertical force to the dry and wet cloths. When pulling up on the center of both cloths with the same force, the height of the wet cloth was lower than that of the dry cloth because of the adhesion force.

[Figure 9] is the result of performing the simulation with and without self-adhesion force in the same frame. Because a liquid bridge is made between the cloth and the object when they collide, and is also made between the cloth and the cloth when it collides with itself, the cloth adheres to itself. If there is no self-adhesion force, after self-collision, the cloth does not adhere to itself, as demonstrated by the dry cloth, although the cloth-object adhesion force and the mass saturation model are applied. However, there is an adhesion force between the cloth and the cloth in the real world, so we express this phenomenon by applying the self-adhesion force to the existing wet cloth simulation.
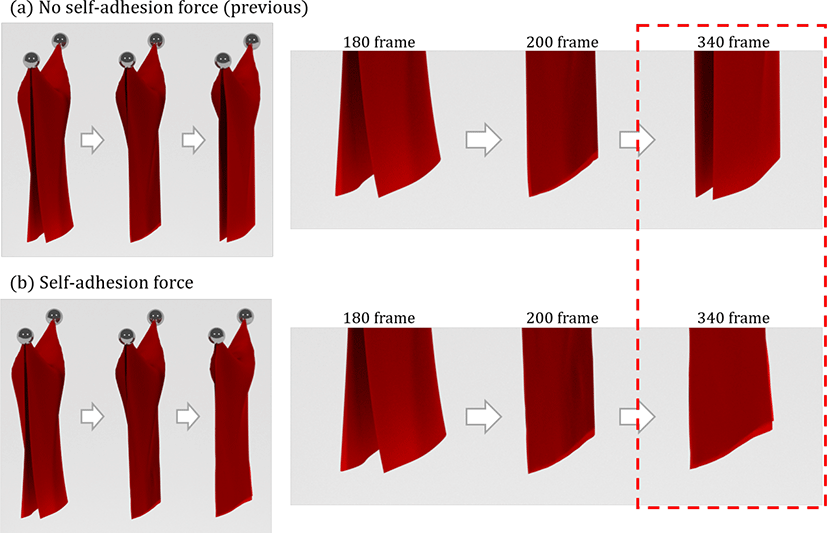
We expressed the adhesive phenomenon between the wet cloth and the object using a theoretically modeled adhesion force model and expressed the adhesive phenomenon after the cloth is collided with itself, the self-adhesion effect, for more realistic results. Differing from previous work that computed the adhesion force based on area, we computed the adhesion force based on the vertex, supposing that each contact vertex has a liquid bridge. Through this method, we can make natural wrinkles that were not expressed in previous work.
We used the mass saturation model to express the increased total mass of the cloth when it is wetted. Because we applied this model to each contact vertex, the cloth model with many vertices was heavy. Thus, we should have adjusted the adhesion force in the model.
5. Conclusion
We have proposed a method that computes the adhesion force based on the vertex. To compute the adhesion force, we used the theoretically-based model of the liquid bridge proposed by [14]. Unlike previous work, in which the adhesion force was computed based on the area and had the same adhesion force for all contacting parts of the cloth, we computed the adhesion force based on the vertex and made different adhesion forces possible for each vertex. Through our method, we can express natural wrinkles at the contact area that were not expressed in previous work. By expressing both the cloth-object and the self-adhesive phenomena, we could achieve a more realistic result.
In fact, wet cloth can show more wrinkles as the object moves. Here we have shown results with simple movements such as ball rotation, but later, we would like to express more realistic wrinkles through interactions with complex moving objects or avatars. In addition, the rendering issue is also important in wet cloth simulation, so we plan to complement the visual results through the method introduced by [13].