Article
입자 기반 유체 시물레이션에서 디테일한 액체 시트를 표현하기 위한 보존과 분해 기법
김종현1,*

Preserving and Breakup for the Detailed Representation of Liquid Sheets in Particle-Based Fluid Simulations
Jong-Hyun Kim1,*

Author Information & Copyright ▼
© Copyright 2019 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Jan 29, 2019 ; Revised: Feb 28, 2019 ; Accepted: Feb 28, 2019
Published Online: Mar 01, 2019
요약
본 논문에서는 입자 기반유체 시뮬레이션에서 과하게 보존되는 액체 시트를 제거함으로써 유체 표면의 디테일을 개선시키는 새로운 방법을 제안한다. 지금까지 울퉁불퉁하고 구멍이 생기는 유체 표면의 고질적인 문제를 해결하기 위한 다양한 비등방성 접근법들은 제안되었지만, 액체 시트의 보존과 분해를 안정적으로 표현할 수 있는 방법은 제시되지 않았다. 본 연구에서는 비등방성 커널과 밀도를 기반으로 하여 물 입자를 동적으로 추가/삭제함으로 입자 기반 유체 시뮬레이션에서 액체 시트의 보존과 분해라는 두 가지 특징을 동시에 표현할 수 있는 새로운 프레임워크를 제안한다. 이 방법은 입자 기반유체 시뮬레이션 접근법에서 과하게 보존되는 액체 시트를 제거함으로써 분열되는 유체 시트의 특징을 잘 표현했으며, 결과적으로 노이즈를 없애 액체 시트의 품질을 개선시켰다.
Abstract
In this paper, we propose a new method to improve the details of the fluid surface by removing liquid sheets that are overpreserved in particle-based water simulation. A variety of anisotropic approaches have been proposed to address the surface noise problem, one of the chronic problems in particle-based fluid simulation. However, a method of stably expressing the preservation and breakup of the liquid sheet has not been proposed. We propose a new framework that can dynamically add and remove the water particles based on anisotropic kernel and density to simultaneously represent two features of liquid sheet preservation and breakup in particle-based fluid simulations. The proposed technique well represented the characteristics of a fluid sheet that was breakup by removing the excessively preserved liquid sheet in a particle-based fluid simulation approach. As a result, the quality of the liquid sheet was improved without noise.
Keywords: 액체 시트; 분해 효과; 유체 표면; 표면 복원; 입자 기반 유체 시뮬레이션
Keywords: Liquid sheets; Breakup effects; Fluid surfaces; Surface reconstruction; Particle-based fluid simulations
1. 서른
유체 시물레이션은 영화, 게임, 영상특수효과, 전산 유체 역학 등 다양한 분야에서 활용되고 있다. 특히, 유체의 움직임을 분석하고 시물레이션하는 것은 비주얼 시뮬레이션 분야에서 유체의 상세한 특징을 캡처하기 위해 반드시 필요한 과정이며, 이 단계는 물, 불, 연기 등에서 모두 공통적으로 필요하다. 연기 시뮬레이션에서는 이산화된 격자의 해상도에 따라 시물레이션 스케일과 디테일이 결정되며, 정해진 격자 해상도 이상으로 유체의 디테일을 표현하는 것은 어렵다. 업 샘플링(Upsampling) 기법은 고해상도 격자가 아닌, 저해상도 격자 공간에서 유체 시물레이션을 계산하고, 고해상도 난류(Turbulence) 모델을 적용함으로써 유체의 디테일을 표현하는 기법이다 [1, 2, 3]. 이 접근법은 저해상도 격자 시물레이션에서 고해상도 난류를 표현할 수 있다는 점에서 효율적이다. 특히, 물 시뮬레이션에서 액체 시트(Liquid sheets) [4, 5], 얇은 유체의 특징 (Thin surface features) [6, 7], 표면장력파(Capillary waves) [8] 등 부드럽고 노이즈 없는 디테일한 유체 표면을 표현하고자 하는 연구들이 꾸준히 발표되고 있다.
본 연구에서는 입자 기반물 시뮬레이션에서 디테일한 유체 표면을 표현할 때 발생하는 새로운 문제에 대해 정의 하고, 이를 해결하기 위한 방법을 소개한다 [4, 5]. 입자 기반 기법으로 유체 시트를 표현하는 방법들이 제시되었지만, 대부분의 접근 법들이 입자의 위치가 고르게 배치되지 않을 경우, 유체 표면에 생성된 구멍(Hole)을 막기 위한 방법으로만 모델링되 었다. 이 방법은 인접 입자들의 정보를 이용하여 구멍 이 발생할 부분을 예측하고, 이 부분에 물 입자를 새롭게 추가하기 때문에 액체 시트가 잘 보존되어 지는 것 처럼 보이지만, 오히려 액체 시트가과하게 보존되어 복잡한 노이즈 표면같이 표현되는 문제로 이어진다 (Figure 1 참조).
Figure 1:
Problem statement : over preserved liquid sheets in particle-based water simulation with previous methods [4, 5].
Download Original Figure
물 입자들 사이에 발생하는 구멍 부근에 새로운 유체 입자를 추가하는 방식은 직관적 이지만 유체 시트가 분해되는 현상이 나타나지 않기 때문에 점성 시트(Viscous sheets)에 가까운 결과가 나타난다. 액체 시트를 표현하는 과정에서 보존과 분해라는 두 가지 특징이 모두 표현되어야 하는데, 기존의 입자 기반 접근법은 결과적으로 이러한 문제를 해결하지 못했다. 본 연구에서는 이러한 문제를 해결하여 디테일한 액체 시트를 표현할 수 있는 프레임워크를 제안하고자 한다.
2. 관련 연구
Osher와 Sethian이 제안한 레벨셋 기법은 물리 기반 시물레이션 및 유동해석에 널리 사용되는 방법 중 하나이다 [9]. 이 방식은 유체의 표면 근처에서 거리 값이 0이 나오는 특징을 기반으로 하여 전체 노드에 대 한 거리 값을 계산하는 방식으로, 복잡한 유체 표면의 토폴로지를 쉽게 표현할 수 있기 때문에 많은 연구들로 개선되 었다[10, 11, 12]. Heo와 Ko는 스펙트럼으로 정제 된 레벨셋 (Spectrally refined level-set) 기법 과 고차정 확도를 갖는 레벨셋 초기화 기법으로 유체의 얇은 표면을 표현할 수 있는 기술을 제안했다 [13]. 그러나 이 방법은 얇은 유체 표면상에서 찢어지 거나분해되는 유체 표면의 특징을 온전하게 표현하기에 충분하지 않았다. 이 이슈를 풀기 위해 메쉬 기반 의 표면 추적 기법들이 제안되 었지만 복잡한토폴로지 변화때문에 알고리즘을 더욱 더 복잡하게 만들었다 [14, 15, 16].
입자 기반 유체 시물레이션에서는 수 많은 입자들로부터 표면을 재구성할 수 있는 다양한 방법들이 제안되었다 [17, 18, 19, 20]. 입자들은 연결 정보가 없기 때문에 인접 입자들로부 터 계산된 밀도로 레벨셋을 근사하여 유체의 표면을 재구성 한다. 그러나 이러한 방법은 울퉁불퉁하고 노이즈한 저품질의 유체 표면을 만들어내고, 특히 입자들의 수가 적은 부분에서 는 표면이 제대로 표현되지 못해 구멍 뚫린 표면이 만들어진다. Ando와 Tsuruno는 FLIP(Fluid-implicit particle) 기반의 유체 시물레이션에서 액체 시트를 생성하고 보존하는 연구를 제안 했다 [4]. 이 방법은 유체 표면 사이에서 구멍이 생성될 때 그 구멍을 막기 위해 새로운 유체 입자를 지속적으로 추가시 켜 유체의 얇은 시트를 보존한다. 또 이들은 비등방성 특성을 고려 하여 유체 시트를 보존할 수 있는 방법을 새롭게 제안함으로 위 기법을 효율적으로 개선시켰다 [5]. 그러나 유체 입자를 두 개 로 분할(Splitting)하고 추가하는 과정에서 유체 시트가 지나치게 보존되어 결과적으로 노이즈한 유체 표면이 만들어 진다 (Figure 1 참조). 최근에는 기 계학습을 기반으로 유체 시물레이션의 디테일과 계산속도를 개선시킨 기법들도 제안되었지만, 효율성 만을 개선하려 노력하였지, 실제로 유체 시트를 표현하기엔 충분하지 않았다 [21, 22, 23, 24, 25]
액체의 얇은 시트 뿐만 아니 라 불연속적인 특징을 표현하려 는 연구들도 꾸준히 진행되어 왔다. 액체가 공기 또는 고체와 맞닿아 있는 인터 페 이 스 부근에서 발생 하는 불연속적인 특징을 정 확하게 계산하기 위해 Ghost fluid method(GFM)를 기반으로 많은 방법들이 제안되어 왔다 [26, 27, 28, 29, 30, 31]. 그 중, Hong 등은 액체와 고체 사이의 인 터 페 이 스에 존재 하는 표면 장력, 점성 등에 GFM 기반의 점프 컨디션을 추가함으로 유체 시뮬레이션의 디테일을 개선시켜 유체의 불연속적인 특징을 훌륭하게 표현했다 [31]. 그러나 이 기법은 오일러 리 안 (Eulerian) 접근법에서만 사용이 가능하기 때문에 입자나 하이브리드 기반에서는 통합되기 어려운 구조라는 한계가 있다.
3. 제안하는 프레임워크
본 논문에서는 유체 시트를 유체 입자들의 움직임에 따라 보 존하고, 불연속적으로 분해함으로 유체 표면의 디테일을 개선시키는 방안을 제시한다. 입자 기반 유체 해법은 FLIP [18]을 이용하였으며, 아래와 같은 순서로 수행된다.
3.1 얇은 입자들을 추출하는 과정
본 연구에서는 얇은 입자들을 추출하기 위해 Ando의 방법 [4, 5]을 기반으로 유체 시트의 보존을 모델링한다. 유체 시트는 유체 표면이 얇게 퍼지는 부분에서 표현되며, 비등방성 커널 (Anisotropic kernel)을 이용하여 이 부분을 찾고, 인접 유체 입자들의 분포를 분석한다. 아래와 같이 유체 입자들마다 가중치 평균 기반의 공분산 행렬 Ci로 입자의 방향성을 계산한다 (Equation 1 참조).
여기서, d0은 유체 입자들 사이의 초기 거리 값을 나타내고, α1는 d0에 대한 가중치 값이다. p̅i는 라플라시 안 스무딩 (Laplacian smoothing)을 이 용한 위치 값이며, Wsmooth는 등방성 가중치 커널이다 (Equations 2과 3 참조).
위 수식으로 계산된 공분산 행렬 Ci는 다음과 같이 SVD를 이용하여 고유 벡터와 고유 값을 얻는데 사용되며, 여기서 인접 유체 입자들 사이의 인장(Stretching)과 방향이 계산된다 :
여기서 en는 분산에 의해 정렬된 주죽을 나타내며, σn는 인장의 크기를 나타낸다. 유체 입자들에서 얇은 입자(thin particle)를 주줄하기 위해 다음 σ3 ≤ α2σ1조건으로 검사했으며, 여기서 α2는 두께의 크기를 결정하는 임계 값이다. Figure 2는 비등방성 커널 기반으로 추출된 얇은 입자들이다. 그림에서 유체 입자들의 움직임을 잘 관찰해보면, 유체 입자들이 퍼져 나갈 때 고체와의 충돌 후부터 얇은 입자들로 추출되는 것을 확인할 수 있다. 즉, 얇은 입자들은 고체와의 충돌 전 상태에서는 추출되지 않고, 고체와의 충돌 후부터 유체 표면의 형태가 얇게 퍼지는 형태로 추출되기 시작한다.
Figure 2:
Selected thin particles from water particles (thin particles are colored red and lie on the outer edge of the fluid body).
Download Original Figure
3.2 유체 시트의 표현을 위한 후보군 입자 추출 과정
추출된 얇은 입자들은 구멍을 막기 위해 필요한 새로운 입자들의 위치를 결정하는데 사용된다. 본 논문에서는 유체 표면에 생긴 구멍을 연결하기 위해 유체 입자의 쌍인, (i,j)를 찾는다. 한 쌍의 중점인, 는 앞으로 분할 될 후보의 위치로 저장 되며, 우리는 아래의 조건을 모두 만족하는 쌍을 선택한다 :
여기서 α3과 α4는 후보군 입자들 사이의 최소, 최대 거리이며, u는 입자의 속도이다. Equation 5a는 두 입자가 서로 적당한 거리에 있는지 검사하는 과정 이며, 거리를 기 반으로 구멍이 존재 하는지를 판단하기 위한 조건이다. Equation 5b는 후보 입자들의 중간 위치에서 반경 α3 내에 유체 입자들이 없고 충 분히 희 박한 영 역 인지를 검 사하는 과정이다. Equation 5c는 입자들 사이의 거리가 시간이 지남에 따라 증가하는지를 검사 하는 과정 이며, 입자들 사이에 생성된 구멍 이 점점 커지는지를 판단하는 조건이다. 이 조건들은 앞에서 추출한 얇은 입자 들로부터 후보군 입자들을 정제하지만, 결과적으로 복잡하고 노이즈한 유체의 표면을 추출하기 때문에 과하게 보존된 유체 시트를 생성한다 (Figure 1 참조). 본 연구에서는 이렇게 과한 유체 시트를 분해하기 위해 아래와 같이 인위적인 조건을 추가한다.
여기서 ρ는 입자의 밀도 이 고, p*는 쌍을 구성 하는 (i, j) 입자 들이다. Equation 6는 쌍의 평균 밀도를 이용한 값이 사용자가 정의한 임계값 τ보다 작은 경우, 얇은 입자 리스트에서 정제 하는데 이용한다. 결과적 로 유체 입자의 쌍은 Equations 5와 6를 모두 만족해야 한다. 쌍을 이루는 입자들의 밀도를 검사 하여 밀도가 작은 부분의 유체 표면이 자연스럽게 찢어지는 것을 표현하기 위해, 쌍을 끊어버 리는 조건을 추가한다. 마지 막으로 위 조건을 모두 만족하는 쌍들의 중간위치를 중복없이 S에 저장한다.
Figure 3은 추출 된 후보군 입자들을 보여주는 결과이다. Figure 3a는 Equation 5를 통해 추출된 후보군 입자들이며, 그림에서 보듯 이 유체 시트가 보존되기 시작하면 분해되지 않고 지속적으로 후보군 입자들을 추출하게 된다. 이 같은 결과는 유체와 고체의 충돌 후에도 계속적으로 후보군 입자들을 추 출하는 결과로 이 어 진다. 그에 반해 Equation 6는 유체 시트 뿐만 아니 라, 얇은 유체의 표면에서 유체 시트의 보존과 분해 효 과를 동시에 잘 표현하였고, 그 결과가 후보군 입자들의 추출 과정에서도 잘 보여 진다 (Figure 3b 참조). 유체와 고체의 충돌 후, 밀도가 매우 작아 표면이 찢어지는 부분에서는 유체 시트가 분해되면서 후보군 입자들의 개수가 점차 줄어드는 결과가 Figure 3a와 비교해 봤을 때 Figure 3b에서 명확하게 나타난다.
3.3 새로운 유체 입자를 주가하는 과정
후보 입자들이 조밀하게 배치되어 있는곳에 새로운 유체 입자를 추가하는 것은 적합하지 않다. 그렇기 때문에 이번장에서는 불필요한 입자를 필터링하고 최소개수의 입자를 추가하여 유체 시트를 보존하는 방법에 대해 설명 한다. I는 앞에서 추출된 최종 후보 입자들의 정보를 저장한 리스트이며, I1는 S에서 첫 번째 위치 값이다:
여기서 ρj는 j번째 입자의 밀도이다. S로부터 I1를 계산한 후, 우리는 sI1의 주변 입자들로부터 반경이 α3d0 내에 존재하는 후보 입자들을 삭제 한다. 그 다음 sI1의 주변 입자들로부터 반경 α3 외부에 있는 입자들을 검색하여 NI1에 추가한다. 마지막으로 NI1에 있는 입자들 중 가장 가까운 입자 sj를 I2에 추가한다 (Equation 8 참조).
입자들을 검색하는 위 수식은 다음과 같이 계산될 수 있다 : In+1 = search(In). 이것은 I2에서도 동일한 방식으로 계산될 수 있음을 의미하고, 해당 문제는 I3, I4, … In+1 와 같이 반복적인 계산으로 풀 수 있다. 만약, 검색 조건이 실패하여 만족하는 후보군 위치가 없다면 Equation 7을 대 신 사용한다.
두 개의 입자로 분할된 후 유체 입자의 속성은 선형 보간 되며, 격자에 매핑된 속도 u와 입자의 밀도 ρ는 아래와 같이 계산된다:
여기서 α5는 속도 u에 대한 가중치 값이고, Wsharp는 아래와 같은 커널 함수 형태이다.
아래 조건 중 하나를 만족할시 유체 입자 i를 삭제한다. (Equations 12과13 참조):
여기서 α6는 최대 밀도 값을 나타내며, α7은 유체 입자들 사이의 최소 거리 값이다. 유체 입자는 Equations 12와 13을 만족하면 제거되며, 그 입자의 질량은 분할 전에 원본 유체 입자에 다시 추가됨으로 보존된다. 유체 입자를 추가/삭제하는 과정은 In이 처리된 다음 In+1이 처리되어야 하는 시리얼 구조이기 때문에 Ando 등이 제안한 알고리즘과 동일하게 처리 하였다 [4, 5].
3.4 유체의 표면 복원
유체 표면을 복원하는 단계에서는 얇은 입자를 추출할 때 사용한 SVD값을 활용한다. 본 논문에서는 Yu 등이 제안한 알고리즘에 SVD의 이방성 특성을 재사용해 유체의 표면을 디테일하게 재구성하였으며 [20], 입자의 레벨셋은 아래와 같이 계산한다 (Equation 14 참조).
여기서 Gi는 유체 입자 i에 대한 변환행렬을 나타내며, 그 속성은 아래와 같다 (Equation 15 참조).
여기서 ks는 스케일링 상수이며, 변화가 가장 큰 인장을 보존하기 위해 σn을 일정 범위 내로 제한하였다. 좀 더 자세한 설명은 Yu 등의 연구를 참조해보길 추천한다 [20]. 본 논문에서는 GPU기반 마칭 큐브(Marching Cubes) 알고리즘을 이용하 였으며 [32], 얇은 유체 표면이 잘 표현되 도록 최소 인장 값을 격자 너비의 절반보다 크게 설정하였다.
4. 구현
본 논문은 다음과 같은 환경에서 구현되 었다 : 인텔 i7-7700k 4.20GHz CPU 32GB RAM, NVIDIA GeForce GTX 1080 Ti 그 래픽카드. FLIP기반 유체 해법을 기반액체 (Underlying water) 시뮬레이션으로 사용했으며 [18], 유체의 압력을 계산하는 수치적 행렬해법은 GPU 기반 선조건 적용 켤레 기을기법(Pre-conditioned conjugate gradient) 방법을 이용하였다 [33]. FLIP격자의 경 우 모든 운동량은 Staggered Marker-and-Cell 방법을 사용해 저장했으며 [34], 표면 재복원을 위해 격자를 추가적으로 사용하였다. 또한, 물과 고체의 충돌처리를 위해 Akinci 등이 제안한 경계 입자(Boundary particle) 기법을 사용하였다 [35].
5. 결과
본 논문에서 는 제안하는 기법을 다양한 방면으로 분석 하기 위해 3가지 시나리오에서 비교해보았다.
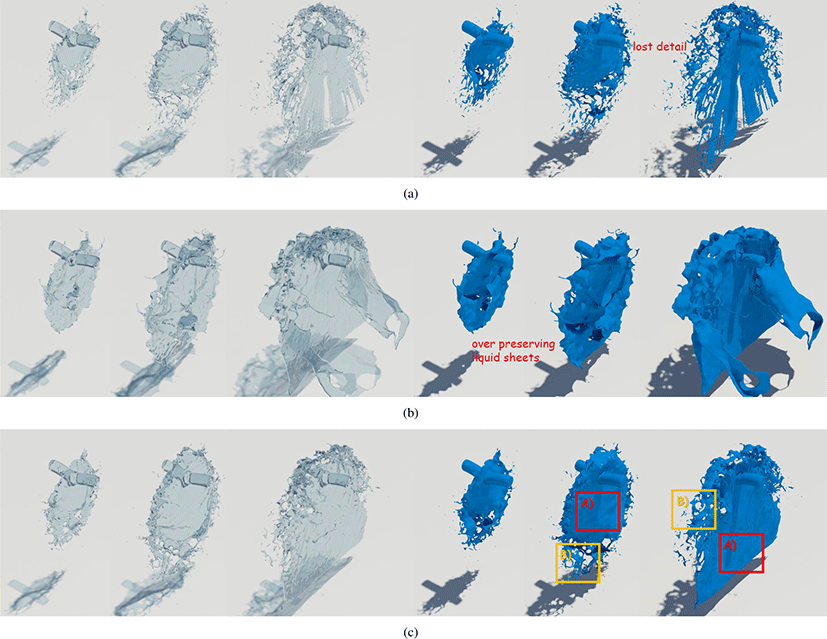
먼저 제안하는 기법의 우수성을 입증하기 위해 간단한 테스트 시나리오로, Stone모델에 구형 액체를 떨어뜨리는 장면을 제작했다 (Figures 4~6 참조). 이 장면에서 유체를 표현하기 위해 타입 스템을 0.006으로 설정하고, 약 15만개의 유체 입자들을 사용하였다. 본 연구에서는 FLIP 기법 [18], Ando의 기법 [4, 5], 제안하는 기법으로 각각 비교하여 유체 시트에 대한 품질을 분석 한다.
Figure 4는 FLIP 기법으로 액체시뮬레이션을 수행한 결과이다. FLIP은 역동적 인 입자들의 움직임을 표현할 수 있기 때문에 액체, 연기, 변형체 등 다양한 재질을 표현하는데 자주 사용된다. 하지만, 그림에서 보듯이 물이 고체와 충돌되 었을 때 스플래쉬(Splash) 형태로 표현되어야 하는 액체 시트가 다 소실되어 버리는 결과가 나타난다. 이 같은 결과는 실제 물리 현상에서 나타나는 물의 표면과는 차이가 생기기 때문에, 이 문제를 완화시키고자 Ando는 소실되는 부분에 새로운 유체 입자를 추가하여 액체 시트를 보존하는 방법을 제안하였다 [4, 5]. 이 접근법은 FLIP 시뮬레이션보다 개선된 결과를 보여주긴 하지만, 표면 소실이 나타나는 구멍에 유체 입자를 추가시 켜주는 단순한조건으로 인해 과도하게 액체 시트가보존되는 결과가 발생 한다 (Figure 5 참조). 유체의 액체 시트는 보존과 분해가 동시에 자연스럽게 표현되어야 하는데, 이 방법에서는 무조건적인 보존 방식으로 인해 디테일한 액체 시트를 표현해내지 못했다. 향후, 적응적 이고 이방성한 계산 프레임워크로 확장하여 액체 시트를 효율적으로 표현해내고자 했지만, 결과적으로 계산의 효율성만 개선되 고 유체 표면의 결과 품질은 개선시키지 못했다 [5]. 그에 비해 본 연구 방법은 앞에서 보여준 결과와 비교해봤을 때 유체 시트의 보존과분해로 디테일함을 잘 표현해 냈다 (Figure 6 참조). 물이 고체와 충돌했을 때부터 유체 시트가 보존되기 시작하고, 유체 표면이 얇아지기 시작 하는 순간부터 불연속적으로 유체 표면이 찢어지는 효과를 잘 표현해 냈다. 액체 시트인지, 점성 재질의 시트(Viscous sheets) 인지 알수 없었던 Figure 5와 비교했을 때 Figure 6는 자연스러운 액체 시트로 잘 표현되 었다.
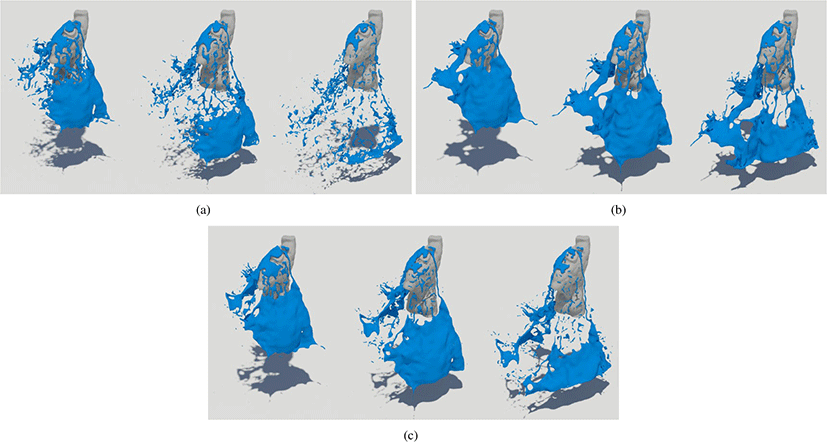
Figure 7은 다른 형태의 고체와 상호작용하는 액체의 움직임을 실험한 결과이며, 마찬가지로 유체 시트의 보존과 분해 효과를 잘 표현해냈다.
Figure 7:
Quality comparison of results using (a) Naïve FLIP simulation [18], (b) Ando’s methods [4, 5] and (c) our method.
Download Original Figure
Figure 8은 두 개의 물 기둥이 서로 충돌해 스플래쉬 형태로 튀는 장면을 제작하고 그에 따른 유체의 움직임을 분석한 것이다. 이 장면에서는 각 물 기둥의 초기 속도만 다르게 하여 충 돌하게 했으며 앞서 본 결과와는 다르게 스플래쉬 형 태의 튀는 움직임이 많이 나타난다. 이 같은 장면에 기존 기법으로 액체의 표면을 표현하게 되면 노이즈를 포함한 유체 표면이 표현 될 뿐만 아니라 점성 시트와 같은 결과가 나타난다 (Figure 8b 참조). 본 연구 기법은 기존의 기법과 비교했을 때 충돌에 의해 발생하는 스플래쉬 효과를 잘 표현해냈으며 (Figure 8b의 B 참조), 동시에 디테일한 유체 시트의 특징도 잘 복원하였다 (Figure 8b의 A 참조). 기존 기법들은 유체 시트의 보존만을 표현하려 했기 때문에 오히려 스플래쉬와 같은 특징이 모두 소실되 었었지만, 본 연구 기법은 유체 시트의 보존과 분해를 온전하게 복원하였기 때문에 Naïve FLIP에 비해 시각적으로 개선된 결과를 보여준다.
Figure 8:
Quality comparison of results using (a) Naïve FLIP simulation [18], (b) Ando’s methods [4, 5] and (c) our method.
Download Original Figure
본 논문에서 제안하는 방법을 다양한 장면에서 실험해본 결과, 이전 기법들에 비해 결과가 개선된 것을 볼 수 있다. 특히, 특정 장면에서만 의존적인 결과를 나타내는 것이 아니라 모든 장면에서 안정적으로 고품질의 액체 시뮬레이션 결과가 나타나는 것을 볼 수 있었다.
Table 1은 본 논문에서 실험한 시뮬레이션 환경과 계산시간을 측정한 값이며, 이전 기법과 계산시간이 거의 비슷함에도 불구하고, 결과품질에 대한 차이가 명확하게 나타난다는 점에서 제안하는 기법의 우수성과 효율성을 다시 한번 확인할 수 있다. Figures 4, 7a, 8a는 Naïve FLIP 시물레이션 이 기 때문에 유체 입자의 개수 변화가 없지만, 나머 지 결과들은 입자들의 평균 개수를 넣어 새로운 유체 입자들을 추가해 매번 유체 시트를 유지했다 (Table 1에서 Num. of particles 참조). 또한, 계산시간은 전체 FLIP시뮬레이션을 포함한 Frames per second로 측정하였다 (Table 1에서 Comp. time 참조).
Table 1:
Size of our example scenes and computational time (Num. : number, Res. : resolution, Comp. : computational).
| Figure |
Num. of particles |
Grid res. for FLIP solver |
Grid res. for surface reconstruction |
Comp. time (sec) |
| 4 |
157,047 |
1203 |
2563 |
0.9 |
| 5 |
161,298 |
1203 |
2563 |
1.42 |
| 6 |
157,787 |
1203 |
2563 |
1.38 |
| 7a |
154,129 |
1203 |
2563 |
0.82 |
| 7b |
161,458 |
1203 |
2563 |
1.29 |
| 7c |
159,914 |
1203 |
2563 |
1.22 |
| 8a |
113,910 |
1203 |
2563 |
0.67 |
| 8b |
142,122 |
1203 |
2563 |
1.83 |
| 8c |
138,703 |
1203 |
2563 |
1.77 |
Download Excel Table
6. 결론 및 향후 연구
본 논문에서는 액체의 디테일한 특징 중 하나인 유체 시트의 보존과 분해를 효율적으로 표현하기 위한 프레임워크를 설명했다. 유체 시트의 보존은 구멍이 생길만한 부분을 찾아내 새로운 유체 입자를 추가해주는 방식을 이용하였으며, 유체 시트의 분해는 얇은 입자들의 쌍을 결정할때 입자들간 변화하는 평균 밀도를 이용하였다. 또, 평균 밀도 값이 매우 작다는 조건을 이용하여 실제로 유체의 부피가 작을 때 분해되는 현상을 표현하였다. 제안된 방법은 특정 장면에서만 유체의 시트를 표현하는 기존 기법과는 달리, 다양한 장면에서 모두 표현 가능한 개선된 결과를 보여주었으며, 유체 시트의 표현으로 인해 상대적으로소실되어버렸던 이전 접근법들에 비해 스플래 쉬 효과도 잘 표현해 냈다.
향후로는, 입자들의 움직임을 매 프레임마다 계산하는 것이 아니라 인공신경망으로 유체의 시트를 학습하고, 이를 통해 유체의 디테일을 효율적으로 표현할 수 있는 방법에 대한 연구를 진행 할 계획이다.
감사의 글
본 연구는 2018학년도 강남대학교 교내 연구비 지원에 의해 수행되었음.
참고 문헌
T. Kim, N. Thürey, D. James, and M. Gross, “Wavelet turbulence for fluid simulation,” in
ACM Transactions on Graphics (TOG), vol. 27, no. 3. ACM, 2008, p. 50.


R. Narain, J. Sewall, M. Carlson, and M. C. Lin, “Fast animation of turbulence using energy transport and procedural synthesis,” in
ACM Transactions on Graphics, vol. 27, no. 5, 2008, p. 166.


H. Schechter and R. Bridson, “Evolving sub-grid turbulence for smoke animation,” in
Proceedings of the 2008 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2008, pp. 1–7.

R. Ando and R. Tsuruno, “A particle-based method for preserving fluid sheets,” in
Proceedings of the 2011 ACM SIGGRAPH/Eurographics symposium on computer animation. ACM, 2011, pp. 7–16.


R. Ando, N. Thurey, and R. Tsuruno, “Preserving fluid sheets with adaptively sampled anisotropic particles,”
IEEE Transactions on Visualization and Computer Graphics, vol. 18, no. 8, pp. 1202–1214, 2012.



X. He, H. Wang, F. Zhang, H. Wang, G. Wang, and K. Zhou, “Robust simulation of sparsely sampled thin features in sph-based free surface flows,”
ACM Transactions on Graphics, vol. 34, no. 1, pp. 7:1–7:9, Dec. 2014.

T. Jang and J. Noh, “A geometric approach to animating thin surface features in smoothed particle hydrodynamics water,”
Computer Animation and Virtual Worlds, vol. 26, no. 2, pp. 161–172, Mar. 2015.


S. Yang, X. He, H. Wang, S. Li, G. Wang, E. Wu, and K. Zhou, “Enriching sph simulation by approximate capillary waves,” in
Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 2016, pp. 29–36.

S. Osher and J. A. Sethian, “Fronts propagating with curvature-dependent speed: algorithms based on hamilton-jacobi formulations,”
Journal of computational physics, vol. 79, no. 1, pp. 12–49, 1988.


D. Enright, R. Fedkiw, J. Ferziger, and I. Mitchell, “A hybrid particle level set method for improved interface capturing,”
Journal of Computational physics, vol. 183, no. 1, pp. 83–116, 2002.


Z. Wang, J. Yang, and F. Stern, “An improved particle correction procedure for the particle level set method,”
Journal of Computational Physics, vol. 228, no. 16, pp. 5819–5837, 2009.


V. Mihalef, D. Metaxas, and M. Sussman, “Textured liquids based on the marker level set,” in
Computer Graphics Forum, vol. 26, no. 3. Wiley Online Library, 2007, pp. 457–466.


N. Heo and H.-S. Ko, “Detail-preserving fully-eulerian interface tracking framework,”
ACM Trans. Graph., vol. 29, no. 6, pp. 176–1, 2010.


C. Wojtan, N. Thürey, M. Gross, and G. Turk, “Deforming meshes that split and merge,” in
ACM Transactions on Graphics (TOG), vol. 28, no. 3. ACM, 2009, p. 76.


M. Müller, “Fast and robust tracking of fluid surfaces,” in
Proceedings of the 2009 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. ACM, 2009, pp. 237–245.


C. Wojtan, N. Thürey, M. Gross, and G. Turk, “Physics-inspired topology changes for thin fluid features,” in
ACM Transactions on Graphics (TOG), vol. 29, no. 4. ACM, 2010, p. 50.


J. F. Blinn, “A generalization of algebraic surface drawing,”
ACM transactions on graphics (TOG), vol. 1, no. 3, pp. 235–256, 1982.


Y. Zhu and R. Bridson, “Animating sand as a fluid,”
ACM Transactions on Graphics (TOG), vol. 24, no. 3, pp. 965–972, 2005.


B. Adams, M. Pauly, R. Keiser, and L. J. Guibas, “Adaptively sampled particle fluids,” in
ACM Transactions on Graphics (TOG), vol. 26, no. 3. ACM, 2007, p. 48.


J. Yu and G. Turk, “Reconstructing surfaces of particle-based fluids using anisotropic kernels,”
ACM Transactions on Graphics (TOG), vol. 32, no. 1, p. 5, 2013.


S. Jeong, B. Solenthaler, M. Pollefeys, M. Gross
et al., “Data-driven fluid simulations using regression forests,”
ACM Transactions on Graphics, vol. 34, no. 6, p. 199, 2015.

J. Tompson, K. Schlachter, P. Sprechmann, and K. Perlin, “Accelerating eulerian fluid simulation with convolutional networks,”
arXiv preprint arXiv:1607.03597, 2016.

K. Um, X. Hu, and N. Thuerey, “Liquid splash modeling with neural networks,”
arXiv preprint arXiv:1704.04456, 2017.

M. Chu and N. Thuerey, “Data-driven synthesis of smoke flows with cnn-based feature descriptors,”
ACM Transactions on Graphics, vol. 36, no. 4, p. 69, 2017.


Y. Xie, E. Franz, M. Chu, and N. Thuerey, “tempogan: A temporally coherent, volumetric gan for super-resolution fluid flow,”
arXiv preprint arXiv:1801.09710, 2018.

M. Kang, R. P. Fedkiw, and X.-D. Liu, “A boundary condition capturing method for multiphase incompressible flow,”
Journal of Scientific Computing, vol. 15, no. 3, pp. 323–360, 2000.


D. Enright, S. Marschner, and R. Fedkiw, “Animation and rendering of complex water surfaces,” in
ACM Transactions on Graphics (TOG), vol. 21, no. 3. ACM, 2002, pp. 736–744.

R. P. Fedkiw, T. Aslam, B. Merriman, and S. Osher, “A non-oscillatory eulerian approach to interfaces in multimaterial flows (the ghost fluid method),”
Journal of computational physics, vol. 152, no. 2, pp. 457–492, 1999.


X.-D. Liu, R. P. Fedkiw, and M. Kang, “A boundary condition capturing method for poisson’s equation on irregular domains,”
Journal of computational Physics, vol. 160, no. 1, pp. 151–178, 2000.


D. Q. Nguyen, R. Fedkiw, and H. W. Jensen, “Physically based modeling and animation of fire,” in
ACM Transactions on Graphics (TOG), vol. 21, no. 3. ACM, 2002, pp. 721–728.

J.-M. Hong and C.-H. Kim, “Discontinuous fluids,” in
ACM Transactions on Graphics (TOG), vol. 24, no. 3. ACM, 2005, pp. 915–920.

C. Dyken and G. Ziegler, “Gpu-accelerated data expansion for the marching cubes algorithm,” in
Proc. PGU Technology Conf, 2010, pp. 115–123.

R. Li and Y. Saad, “Gpu-accelerated preconditioned iterative linear solvers,”
The Journal of Supercomputing, vol. 63, no. 2, pp. 443–466, 2013.


F. H. Harlow and J. E. Welch, “Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface,”
The physics of fluids, vol. 8, no. 12, pp. 2182–2189, 1965.


N. Akinci, J. Cornelis, G. Akinci, and M. Teschner, “Coupling elastic solids with smoothed particle hydrodynamics fluids,”
Computer Animation and Virtual Worlds, vol. 24, no. 3-4, pp. 195–203, 2013.


T. Jang and J. Noh, “A geometric approach to animating thin surface features in smoothed particle hydrodynamics water,”
Computer Animation and Virtual Worlds, vol. 26, no. 2, pp. 161–172, 2015.


S. Yang, X. He, H. Wang, S. Li, G. Wang, E. Wu, and K. Zhou, “Enriching sph simulation by approximate capillary waves.” in
Eurographics/ACM SIGGRAPH Symposium on Computer Animation, 2016, pp. 29–36.

M. Müller, D. Charypar, and M. Gross, “Particle-based fluid simulation for interactive applications,” in
Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2003, pp. 154–159.