부채꼴 영역 기반의 동적인 충돌 영역을이용한입자 기반충돌검사의 고속화기법

김, 종현

doi:10.15701/kcgs.2019.25.2.11

J Korea Comput Graph Soc 2019; 25(2):11-18

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2019.25.2.11

Article

부채꼴 영역 기반의 동적인 충돌 영역을이용한입자 기반충돌검사의 고속화기법

김종현 ¹ ^, ^*

Acceleration Technique in Particle-based Collision Detection Using Cone Area Based Dynamic Collision Regions

Jong-Hyun Kim ¹ ^, ^*

Author Information & Copyright ▼

¹강남대학교

¹Kangnam University

^*corresponding author: Jong-Hyun Kim/Kangnam University(jonghyunkim@kangnam.ac.kr)

© Copyright 2019 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Mar 04, 2019 ; Revised: Apr 30, 2019 ; Accepted: May 15, 2019

Published Online: Jun 01, 2019

요약

본 논문에서는 많은 개체와의 충돌 검사를 요구하는 입자 기반 시스템에서 부채꼴 영역의 동적인 변화를 이용하여 효율적으로 충돌 검사를 가속화시킬 수 있는 프레임워크를 제안한다. 입자와 부채꼴 기반의 충돌 영역은 다음 세 가지 조건에 의해 결정된다: 1) 인접 입자의 반경 내에 부채꼴의위치가 존재하는 경우, 2) 부채꼴 영역 내에 인접 입자의 위치가 존재하는 경우, 3) 부채꼴 영역을 형성하는 두 벡터 사이에 인접 입자가 존재하는 경우. 결과적으로 위 조건들 을 모두 만족했을 때 입자와 부채꼴 영역은 충돌되었다고 정의한다. 본 논문에서는 입자의 움직임에 따라 충돌 검사 범위인 부채꼴의 영역을자동으로 업데이트 한다. 부채꼴 영역의 동적인 변화를 계산하기 위해 입자의 위치와 속도를 기반으로 부채꼴의 방향, 길이, 각도를 조절한다. 최종적으로 계산된 부채꼴 영역 내에 있는 입자들만을이용하여 충돌 검사를 빠르게 수행한다. 본 연구에서 제안하는 가속화 방법은 트리와 같은자료구조를 명시적으로 만들지 않고, 닫힌 형태 방정식으로 실행되기 때문에 간단하게 구현되며모든 결과에서 충돌 검사 성능이 개선되었다.

Abstract

In this paper, we propose a framework that can perform acceleration collision detection efficiently by using a cone based collision area in a particle-based system which requires collision detection with many objects. Three conditions determine particle and cone-based collision regions: 1) If there is a cone position within the radius of the adjacent particle, 2) In the case where the position of the adjacent particle exists in the cone area, 3) When adjacent particles exist between two vectors forming a cone area. As a result, it is defined that when the above conditions are all satisfied, the particle and the region of a cone have collided. In this paper, we automatically update the area of the cone, which is the collision detection area, according to the particle movement. Determine the direction and length of the cone based on the position and velocity of the particle to calculate the dynamic change of the cone. Collision detection is performed quickly using only the particles in the finally calculated area. The acceleration method proposed in this paper is simple to implement because it is executed with a closed form equation instead of explicitly creating the tree data structure, and collision inspection performance is improved in all results

Keywords: 충돌 검사; 동적인 충돌 영역; 입자 기반 충돌 감지

Keywords: Collision detection; Dynamic collision area; Particle based collision detection

1. 서론

입자 기반 시스템은 물리 기반 시뮬레이션, 렌더링, 게임, 영상 특수효과 등 다양한 분야에서 사용되고 있다 [1, 2]. 일반적인 강체나 변형체와는다르게 입자 기반 시스템은 충돌 검사하는 개체의 수가 굉장히 많기 때문에 이를 효율적으로 다루고자 팔진/쿼드 트리(Octree/Quad tree) [3], K-d 트리 [4], 해시 테이블 [5] 등 다양한 최적화 방법들이 사용되고 있다. 하지만, 이러한 가속화 자료구조는 입자의 위치가 변경되면 매번 자료구조를 업데이트를 해야 되기 때문에 메모리와 계산속도 측면에서 비효율적이다. 이 문제는 실시간을 요구하는 게임이나 가상현실 콘텐츠 분야에 활용하기에 적합하지 않고, 충돌 검사할 개체의 수가 적다면 오히려 앞에서 언급한 가속화 자료구조를 생성하는 과정에서 계산 속도가 더 오래 걸리는 상황이 발생 하기도 한다. 본 논문에서는 2차원 공간상에서 이러한 문제를 해결하기 위해 입자의 위치와 속도를 기반으로 부채꼴 영역을 동적으로 변경하고 이 영역을 활용하여 충돌 검사를 가속화하는 새로운 자료구조를 제안한다.

2. 관련 연구

이장에서는 입자 기반 충돌 검사를 효율적으로 처리할 수 있는 방법에 대해 간략하게 살펴본다.

많은 개수의 입자들에서 충돌 검사를 효율적으로 처리할 수 있는 공간 분할 기반의 가속화 방법은 크게 두 가지 범주로 나뉜다 : 1) BVH(Bounding volume hierarchies)를 활용한 적응형 구조로 Octree, K-d 트리, BSP(Binary separating planes) 트리, OBB(Oriented bounding box) 트리, 2) 정규격자를 활용 해시 테이블(Hash table).

BVH는 충돌 검사를 가속화하기 위해 간단한 경계 볼륨의 계층적 배열을 사용하는 데이터 구조의일반적인 용어이다 [6, 7]. 예를 들어, 임의의 3차원 모델에 대해서 교차점을 검사하려면 먼저 그 모델을 감싸고 있는 최상위 경계 볼륨에 대해 먼저 충돌 검사를 해야 한다. 경계 볼륨에서 충돌이 발생하면, 다음 레벨인 3차원 모델을 구성하고 있는 삼각형들에 대해서 충돌 검사를 진행한다.

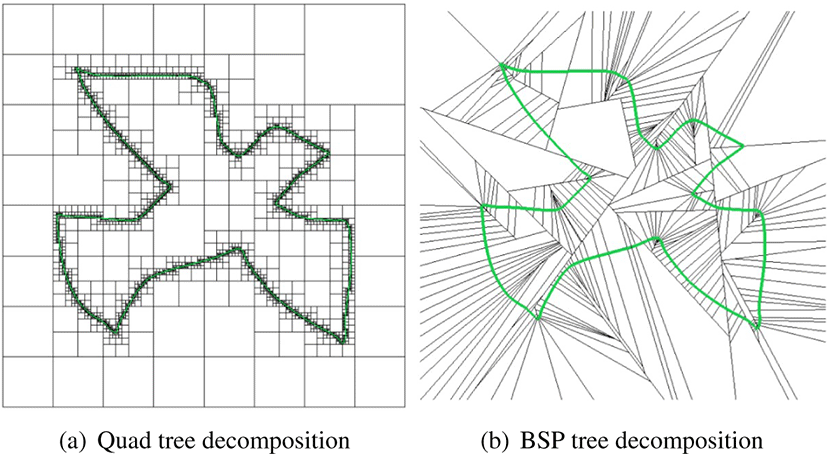
Octree는 BVH를 활용한 이진 트리형 자료구조로 8개의 자식 입방체를 각각 포함하는 트리 구조를 사용한다 (2차원에서 는 Quad 트리) [3, 8]. 객체가 존재하는 곳에서만 분할이 진행 되기 때문 적응형 공간 분할 구조라고도 부르며, Octree의 말단 노드에는 결과적으로 실제 객체인 삼각형들을 포함하고 있는 공간들이 추출된다 (Figure 1a 참조).

Figure 1: Quad tree and BSP tree.

Download Original Figure

K-d 트리는 앞에서 언급한 Octree와는다르게 하나의 x, y 또는 z 평면에 따라 두 개의 공간으로 분할하는 구조를 사용한다. 일반적으로 자식 노드가 Octree에 비해 적기 때문에 트리의 크기가 작다. K-d 트리의 특징중 하나는 검색해야 될 영역의 크기가 매번 다를 경우 트리 검색을 통해 빠르게 찾을 수 있다. 검색 범위가고정된 경우는 정규 격자가 효율적이지만, 그렇지 않은 경우는 K-d 트리가 더 빠르게 때문에 고속화 광선 추적법에서 자주 사용된다 [9, 4, 10].

BSP 트리는 임의의 평면을 사용하여 공간을 작은 영역으로 나누는 기법이다. 이름에서 알 수 있듯이이 기법 또한 공간 분할 구조이며, 충돌 처리 뿐만 아니라 로보틱스 분야에서도 자주 활용되고 있다 (Figure 1b 참조).

OBB 트는 회전된 상자의 계층 구조를 사용하여 객체의 형상에 가깝게 경계 상자를맞추는 기법이다 [11, 12]. 경계 상자는 계층을 구성하는 과정에서 상자끼리 겹칠 수 있으므로 공간에 파티션을 구성하지 않는다.

정규격자는 앞에서설명한 방법과는다소 차이가 있으며, 공간을 동일한 상자로 분할하는 비계층 구조이다 [13, 5]. 이 자료구조는 빠르게 수행되지만 복잡한 장면에서는 메모리가 비효율적으로 사용된다.

이 외에 공간 분할 접근법을 활용한 충돌 검사는 크게객체 공간과 이미지 공간으로 구분할 수 있다. 객체 공간 접근법은 일반적으로 객체의 토폴로지와 지오메트리 정보를 이용하여 충돌 검사를 계산한다. 이미지 공간 접근법에서 3차원 객체의 정보를 2차원 이미지 공간으로 변환하고 저장하기 때문에 계산양이 적고 충돌 처리가 빠르게 수행된다.

최근에는 하드웨어 가속화된 접근법들이 제안되고 있다. Knott와 Pai는 그래픽하드웨어를 사용하여 다면체 간의 충돌을 검출해냈다 [14]. 이 기법에서는 가상의 레이 캐스팅 기법을이용하여 다면체 사이에서 발생하는 충돌을 감지했다. Govindaraju 등은 충돌 처리가 상대적으로 많이 발생하는 변형 체와 파괴 시뮬레이션에서 효율적으로 활용할 수 있는 알고리 즘을 제안했다 [15]. Greβ와 Zachmann은 다각형 모델의 충돌 검사에서 발생하는 교차점 계산을 그래픽하드웨어 기반으로 처리했다 [16]. 이 방법은 BVH에서 발생하는 트리 순회 과정 을 GPU상에서 한 번에 처리하기 때문에 충돌 검사가 빠르다. Govindaraju 등은 GPU상에서 가사성 쿼리를 계산함으로써 객체 간의 충돌 검사를 가속화 했다 [17].

Sigg 등은 하드웨어 가속으로 부호 거리장(Signed distance field)을 계산하여 충돌 검사를 가속화했다 [18]. 이들은 GPU 상에서 부호 거리장을 계산할 때, 제한된 영역인 로컬 거리장 을 활용하여 거리장을 빠르게계산했다. Kipfer 등은 행 정렬 (Row sorting) 기법을 제안하여 입자의 움직임을 시뮬레이션하 고, 입자 간의 충돌을 근사하는 기법을 제안했다 [19]. 이들은 메모리 압축 기법이라는 높이 필드장을 이용하여 장면을 구성 했지만, 복잡한 3차원 모델을 표현하는데 있어서는 충분하지 않았다. Kolb 등은 많은 개수의 입자 시스템에서 발생하는 충돌 처리를 깊이 맵을이용하여 효율적으로 처리했다 [20]. Sud 등은 보로노이 특징을 기반으로 부호 거리장을 구축했고, 이 과정을 그래픽하드웨어에서 처리함으로써 빠르게 충돌 처리를 수행하였다 [21]. Chen 등은 그래픽하드웨어를 사용하여 변형체 간의 충돌을 빠르게감지하는 기법을 제시했다 [22]. Govindaraju 등은 그래픽하드웨어를 기반으로 모델 간의 충돌 검사 횟수를 줄이기 위한 새로운 컬링 알고리즘을 제시했다 [23]. Wong과 Baciu은 GPU를 이용하여 변형체 시뮬레이션 에서 발생하는 충돌 검사를 빠르게계산할 수 있는 프레임워크를 제안했고 [24], 향후 GPU 기반 연속 충돌 검사(Continuos collision detection)로 확장하여 실시간 충돌 처리를 가능케 했다 [25].

3. 제안하는 방법

3.1 입자와 부채꼴 영역과의 충돌 검사

제안하는 방법은 두 가지 단계로 구분되어 실행된다 : 1) 정적 인 부채꼴 영역과 입자와의 충돌 검사이며, 2) 입자의 위치와 속도를 기반으로 부채꼴 영역을 업데이트하여 충돌 검사를 수 행할 영역의 크기를 자동적으로 결정하는 것이다.

첫번째 조건을 모델링하기 위해 입자는 SPH(Smoothed particle hydrodynamics)와 마찬가지로 유한한 영역을 가진다고가 정하고, 아래와 같은 세 가지 종류의 충돌 검사를 수행한다 (Figure 2 참조). 이 그림에서 부채꼴의 중심 위치인 검정색 입자는 충돌 검사를 수행하는 입자의 위치이고, 그 외 빨간색과 회색 입자들은인접 입자들이다.

Figure 2: Various types of collision detection : a) cone area and particle radius, b) cone area and particle position, c) no collision. Arrows indicate the velocity for each particle.

Download Original Figure

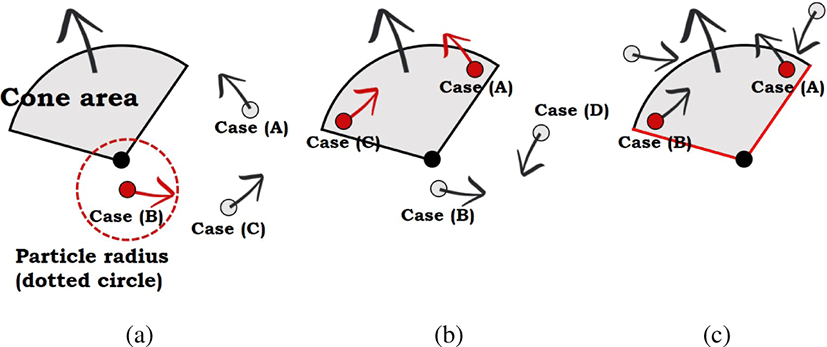
Figure 2a에서는 부채꼴 영역과 인접 입자의 반지름 영역 간에 충돌이 발생하는 장면이다. 대분의 입자 기반 시스템에서는 물리량을 계산하는 유한한 반경이있고, 이 경우에서도 마찬가지로 그림 내 빨간색 원을유한한 반경이라고가정하고 계산한다. Figure 2a에서 Case (A,B)는 입자들이 부채꼴 영역 내에없지만, Case (B)는 반지름 영역 내에 부채꼴의위치가 포 함되어 있기 때문에 충돌이라고 판단한다.

Figure 2b에서는 인접 입자의 위치가 부채꼴 영역 내부에 존 재하는 경우이며, 대부분의 경우가 Figure 2a에서 필터링이 되 겠지만, 입자의 속도가 빠른 경우 Figure 2b에 속하게 되어, 입 자들이 부채꼴 영역 내부에 배치된다 (Case (A,C) 참조).

마지막으로 Figure 2c에서는 Figure 2a,b의 경우를 좀 더 정확하게 찾는 조건이다. 실제로 부채꼴 영역 내부에서만 충돌이 발생해야 되기 때문에 부채꼴 영역을 정의할 때 필요한 벡터를 이용하여 이 벡터 외부에 있는 영역은 충돌 검사 계산 과정에서 제외하며 (Figure 2c에서의 빨간색 선), 결과적으로 Case (A,B)만 충돌처리에 포함된다.

앞에서 언급한 세 가지 조건을 개발하기 위한 자세한 수치 기법은 다음과같다 :

부채꼴 영역의 중심 위치가 인접 입자의 반지름 영역 내부에 있을 경우 (Figure 2a 참조)

이 같은 경우는 2차원원 방정식의음함수를 활용하여 계산 할 수 있다 (Equation 1 참조).

(x p − x c) 2 + (y p − y c) 2 − r p 2 < 0

(1)

여기서 (x_p,y_p)와 (x_c,y_c)는 각각 인접 입자와 부채꼴의위 치이며, r_p는 입자의 유한한 영역을 나타내는 반지름이다. 여기서 반지름은 입자와 부채꼴 영역간의 충돌 검사를 수행할 때의 반경이며, 결과적으로 부채꼴 영역의 중심이 입자의 반 경 내부에 존재하면 Equation 1을 만족하기 때문에 충돌이 발생된 상황으로 판단한다.

두번째와 세번째 조건은 부채꼴 영역을 구성하는 두 벡터의 내분을 활용하여 계산한다.

입자의 위치가 부채꼴 영역의 내부에 있을 경우 (Figure 2b 참조)
입자의 위치가 부채꼴 영역을 형성하는 두 벡터 사이에 있고, 입자의 위치로부터 부채꼴 위치까지의 거리가 입자 의 반지름과 부채꼴 길이의 합보다 작다면 충돌 (Figure 2c 참조)

입자가 부채꼴 영역 내에 있다면 위 가정은 부채꼴 영역을 구성하는 두 벡터 vec₁과 vec₂ 사이에 존재한다고 말할 수 있고, 본 연구에서는 이 조건을 아래와 같이 계산한다 (Equation 2 참조).

P − C = α ⋅ v e c 1 + β ⋅ v e c 2

(2)

여기서 P는 인접 입자의 위치 (x_p,y_p)이고, C는 부채꼴의 중심위치 (x_c,y_c)이다. α와 β는 0보다 큰 가중치이고 벡터의 내분을 계산할 때 사용되는 값이다. Equation 2는 벡터의 내분 을 활용한 수식이며, 결과적으로 두 벡터 vec₁과 vec₂ 사이를 t :1 − t 비율로 내분하는 수식이다. 본 연구에서 1 − t는 α 이며 t는 β이다. 두 벡터 공간 사이에 입자가 위치한다면 α와 β는 0보다 크거나 같고, 둘의 합은 1이 되며,1보다 큰 경우 부 채꼴 영역 외부에 있다고 판단한다. 하지만, 이 조건만 적용할 경우 Figure 2c에서 보듯이 두 벡터를 포함하는 모든 공간에 대해서 충돌되었다고 잘못 판단된다. 우리가 원하는 부채꼴 영역은 회색 부분이지만, 결과적으로 흰색 영역까지 포함된다 (Figure 2c 참조).

본 연구에서는 이 문제를 피하기 위해 추가적인 조건을 사 용한다. 부채꼴의위치에서 입자 위치로의 방향벡터 길이를 비교하여 이 길이가 vec₁의 크기보다 작은 경우에만 충돌되었 다고 판단한다 (Equation 3 참조).

‖ P − C ‖ < ‖ v e c 1 ‖

(3)

부채꼴 영역을 구성하는 vec₁과 vec₂는 같은 크기이기 때문 에 위 수식에서 vec₁이라고 했지, vec₂로 변경해도 같은 결과 가 나온다. Equation 2와 3는 부채꼴 영역을 검사하는 수식은 아니다. 하지만, 본 연구에서는 입자들이 부채꼴 영역 내에 들어왔는지를 확인하기 위한 길이만 알면 되기 때문에 부채꼴을 구성하는 두 벡터를 이용하여 알고리즘을 디자인하였다. 결과적으로 앞에서 언급한 세 가지 조건을 모두 만족하는 경우에 입자와 정적인 부채꼴 영역은 충돌한다.

3.2 부채꼴 영역업데이트

본 논문에서는 부채꼴 영역에 동적인 변화를 추가하여 입자의 움직임에 따라 충돌 영역으로 사용하는 부채꼴 영역을 업데이트시킨다. 이 방법을 구현하기 위해 입자의 위치와 속도를 이용하였으며, 이 속성들로부터 부채꼴의위치, 각도, 길이를 조절한다.

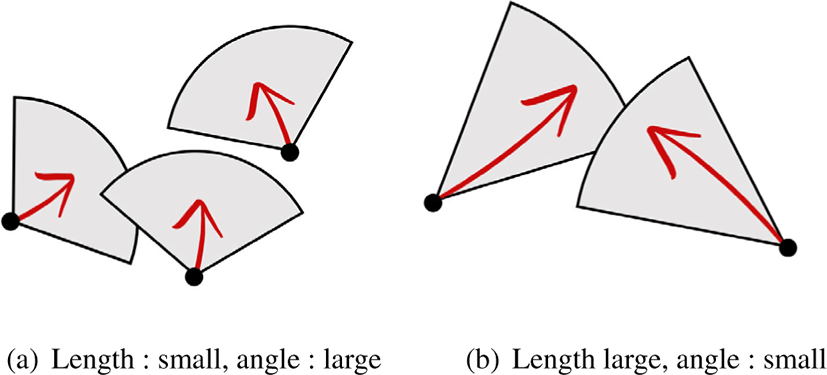
Figure 3에서는 입자의 속도를 기준으로 두 가지 상황에 대해서설명한다. Figure 3a는 입자의 속도가 느린 경우이다. 부채꼴의 방향은 입자의 속도와 같은 방향으로 설정하고 부채꼴의 길이는 짧게 설정한다. 실제로 입자의 속도가 느린 경우 속도 방향보다는 오히려 양옆에서 갑자기 충돌될 가능성이 높기 때문에 본 연구에서는 부채꼴의 길이는 짧게, 각도는 넓게 설정하였다. Figure 3b는 빠른 속도로 움직이는 입자의 경우이 다. 이 같은 경우는 속도가 빠르기 때문에양옆보다는 입자의 빠른 속도로 인해 지나쳐가는 영역에서 충돌될 가능성이 높기 때문에 상대적으로 부채꼴의 길이는 길게, 각도는 짧게 설정 하였다.

Figure 3: Area of the cone that varies with the particle velocity (red arrow : particle velocity).

Download Original Figure

앞에서 언급한 상황을 구현하기 위해 부채꼴의위치 C는 충돌 검사를 진행하는 입자의 위치로 설정한 뒤 부채꼴의 길이 l_c를 계산한다 (Equation 4 참조).

l c = ‖ v c ‖ δ

(4)

여기서 v_c는 부채꼴 영역을 정의하는 입자의 속도이며 δ는 부채꼴의 길이를 조절하는 가중치이다. 부채꼴의 각도 a_c는 최소와 최대 각도를 설정한 뒤 그 사이 값을 v_c의 크기에 따라 보간하여 매번 업데이트한다 (Equation 5~7 참조).

a c = (1 − w *) a c max + w * ⋅ a c min

(5)

w * = γ + log 3 w γ

(6)

w = min (max (l c, ‖ v c min ‖), ‖ v c max ‖) ‖ v c max − v c min ‖

(7)

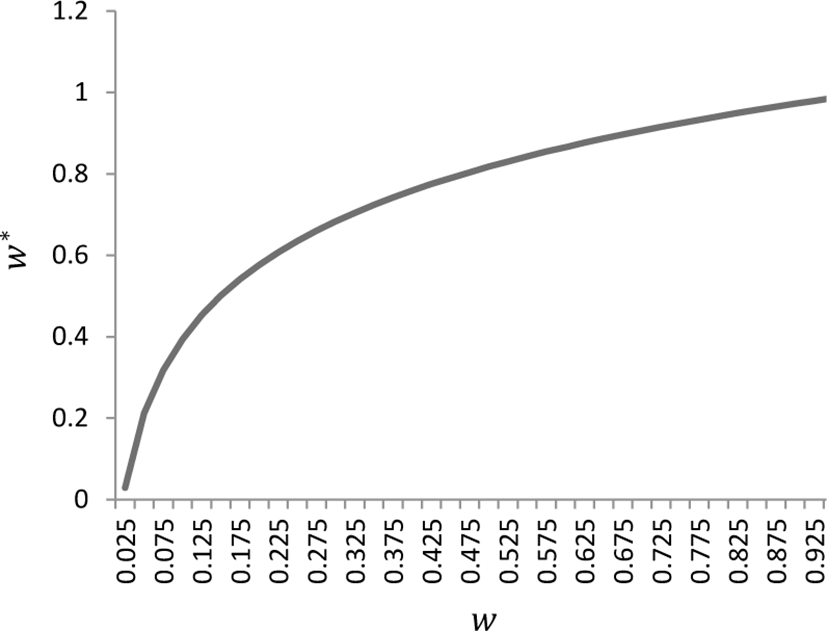
여기서 w는 각도를 보간하기 위한 가중치이며, 입자의 속도를 고려하여 부채꼴의 각도를 결정한다. 입자의 속도가 느리거나 빠를 경우 w값이 과하게 증감하는 경우가 있고, 이 같은 문제는 시뮬레이션의 안정성을 떨어뜨리는 요인이 된다. 이를 완화하기 위해 w를 정제한 w^*를 이용하여 각도를 보간한다.

Figure 4는 w^*의 변화를 보여주고 있는 차트이며 입자의 속 도에 따라 선형적으로 증가하는 w보다 안정적으로 부채꼴 영역을 얻을 수 있다. 입자의 속도에 따라 변화하는 부채꼴 영역은 충돌 검사에서 있어 중요한 역할을 하며, 실제로 w^*의 기울 기를 보면 입자의 속도가 증가하기 시작하는 부분(w :0.075 ~ 0.175)에서 기울기가 크고, 결과적으로 부채꼴의 각도가 빠르 게 증가하게 된다. 상대적으로 입자의 속도가 이미 빠른 상태 에서 더 빠르게 움직인다고 하여 각도를 넓히는건 부채꼴 영역이 과하게 넓어질 수 있기 때문에 입자의 속도가 빠를수록 w^*의 기울기를 완화시키는 형태로(w :0.675 ~ 0.825) 커널을 계산했다.

Figure 4: The shape of weight function inside the kernel w^*

Download Original Figure

4. 결과 및 분석

4.1 장면 초기화

제안된 부채꼴 영역 기반의 동적인 충돌 영역 기법을 다양한 방면으로 분석하기 위해 몇 가지 시나리오에 대해서 우리의 방법을 비교한다. 기본적인 시나리오는다음과같다 : 충돌 검사를 수행하고자 하는 위치와 인접 입자들은유체 시뮬레이션 과같이 매 스텝 움직인다.

고정된 위치가 아니라 SPH와 같이 시간에 따라 입자들이 움직이는 상황에서 충돌 검사를 진행한다. 입자들이 움직이게 되면 가속화 자료구조는 매번 업데이트해야 되기 때문에 계산양이 커진다. 우리는 본 연구의 가속화 측면을 분석하기 위해 계산양이 비교적 큰 시뮬레이션 환경에서 기존 기법들과의 비교를 수행한다.

4.2 결과

우리는 간단하고 직관적인 시나리오에서 제안하는 기법의 우 수성을입증하기 위해 제한된 영역 내에 랜덤하게 수많은 입자 를 배치시켜 충돌 검사를 계산하였다 (Figure 5 참조). 우리는 2 차원에서 10,000개의 입자를 사용했으며 충돌 검사를 수행해 야하는 위치는 빨간색 구이며, 사용자가 지정한 반지름 영역 내에 존재하는 입자를 충돌된 입자라고가정하고 장면을 구 성하였다.

Figure 5: Collision detection with brute-force search (green particle : collided particle, red sphere : target position).

Download Original Figure

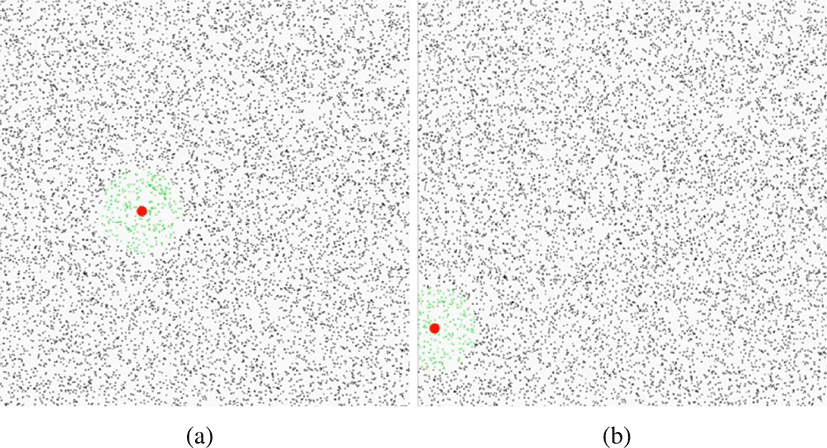
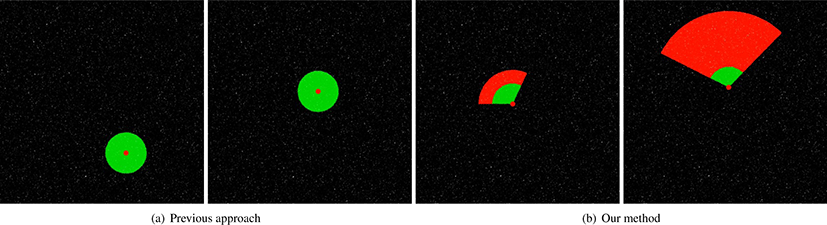
가장 간단한 방법은 전체 입자들에 대해서 충돌 검사를 수 행하는 방식이며, 이 같은 방식은 빨간색 구를 중심으로 충돌 된 녹색 입자를 찾는 과정에서 입자의 속도에 관계없이 전체 입자들에 대해 충돌 검사를 수행하기 때문에 불필요한 계산이 추가된다. Figure 5의 결과는 빨간색 입자의 움직임은 고려되지 못한채 단순하게 위치만을이용하여 충돌하는 방식이며, 충돌 검사에서 평균 0.003초가 소요됐다.

Figure 6은 제안된 방법으로 충돌 검사를 수행한 결과이다. Figure 5와 동일한 환경에서 실험했으며, 본 논문에서 제안한 기법은 충돌 검사 과정에서 평균 0.0005초가 소요됐다. Figure 6a는 입자의 속도가 빠르게 움직이는 상황에서 부채꼴 기반 충돌 검사를 계산한 결과이며, Figure 6b는느린 속도에서 계산한 결과이다. 빨간색 입자는 3장에서 제안한 부채꼴 영역 내에 존재하는 입자들이며 Figure 5에서 모든 입자들이 충돌 후보군에 속하는 것과 달리 Figure 6에서는 빨간색 입자들이 충돌 후보군에 속하기 때문에 그 개수가 월등히 줄어들었으 며,3배 정도의 계산속도가 향상되었다.

Figure 6: Collision detection with our method (red particle : candidate particle, green particle : collided particle, red sphere : target position).

Download Original Figure

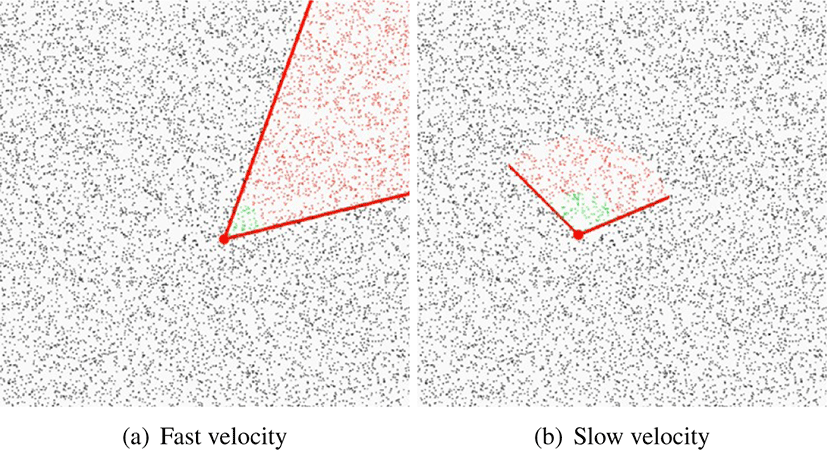
또한 Figure 5에 비해서 충돌된 녹색 입자 개수도 월등히 줄 어들었다. 빨간색 원이 고정된 상태라면 원 형태로 녹색 입자 들이 추출되겠지만, 본 논문에서는 입자들이 움직이기 때문 에 움직이는 방향으로 녹색 입자들이 추출된 결과를 보여준다. 그림에서 빨간색 입자들은 충돌 검사를 수행할 입자들이 며모든 입자들에 대해서 충돌 검사를 수행한 Figure 5에 비해 그 개수가 월등히 줄어들었다. 뿐만 아니라 안정적으로 충돌 검사를 수행하기 위해 입자의 속도에 따라 영역이자동으로 업데이트 되었으며, 앞에서설명했듯이 부채꼴 영역이 다르게 나타나는 것을 쉽게 볼 수 있다 (Figure 6 참조).

우리는 좀 더 많은 입자들에 대해서 실험을 했다. Figure 7은 500,000개의 입자를 사용하여 충돌 검사를 수행한 결과이며, 앞에서의 결과와 마찬가지로 충돌 검사에서 이전 기법은 평균 0.15초, 제안된 기법은 0.03초가 소요되었다.

Figure 7: Collision detection with our method (red particle : candidate particle, green particle : collided particle, red sphere : target position).

Download Original Figure

4.3 이전 기법과의 비교

본 연구에서는 가속화 자료구조로 많이 사용되고 있는 K-d 트리와 해시 테이블의 결과를 제안한 연구와 비교했으며 (Figure 8 참조), 충돌 검사 환경은 Figure 5와 같다.

Figure 8: Collision detection comparison of results using (a,b) K-d tree and (c,d) hash table (red particle : candidate particle, green particle : collided particle, red sphere : target position).

Download Original Figure

Figure 8a,b는 K-d 트리를 구성할 때 다양한 버킷크기에 따른 결과를 분석하기 위해 만든 결과이며 버킷크기가 작을수록 최대 트리 깊이가 커진다. K-d 트리를 통해 충돌 후보군으로 추출된 부분은 빨간색 박스로 표시한 부분이며 해당 노드에 포함되어 있는 입자들만을이용하여 최종 충돌 검사를 수행 한다. Figure 8a에서 보듯이 녹색 입자들이 최종 충돌된 입자 이며 이를 수행하는데 걸린 시간은 0.002초이며, 500,000개의 입자에서 충돌 검사를 수행했을 때는 0.13초가 소요됐다. 트리를 매번 재구성해야 되는 계산양 때문에 입자의 개수가 늘어날 수록 충둘 검사 시간이 증가된다. 버킷크기가 좀 더 큰 Figure 8b에서는 10,000개의 입자에서 충돌 검사를 수행했을 때 0.003초가 소요됐고, 500,000개의 입자에서는 0.14초가 소요됐다. 버킷크기에 따라 약간의 차이만 있을 뿐 성능향상이 없었다.

Figure 8c,d는 해시 테이블을이용하여 충돌 검사를 수행한 결과이다. 테이블을 구성할 때 다양한 해상도로 충돌 실험했으며 Figure 8c,d의 충돌 검사에서 소요된 시간은 모두 0.001 초가 소요되었다. 500,000개의 입자에서도 모두 0.04초가 소 요됐다.

Table 1은 본 연구의 결과들을 제작하는데 소요된 계산시간을 요약한 표이다. 본 논문에서 실험한 환경은 0에서 1사이의 공간에서 랜덤하게 입자들을 배치시키고 충돌 검사를 수행하였다. 시간에 따른 입자들의 움직임은 허용된 범위내에 지터 (Jitter)를 두어 입자들이 매 스텝 조금씩 움직이도록 설정하였고, 결과적으로 움직이는 입자들 내에서 충돌 검사를 위한 실험 장면을 구축했다.

Table 1: Comparison of the calculation time of the previous and our method (computation time : sec, bucket size of K-d tree : 10/100, resolutoin of hash table : 30/15).

Num. of particles	Brute-force search	K-d tree:10/100	Hash table:30/15	Our method
10,000	0.003	0.002/0.003	0.001/0.001	0.0005
500,000	0.15	0.13/0.14	0.04/0.04	0.03

Download Excel Table

5. 결론 및 향후 연구

지금까지 입자의 속도에 따라 변화하는 부채꼴 영역을이용 하여 2차원 공간상에서 충돌 검사를 빠르게 수행하기 위한프 레임워크에 대해 설명했다. 부채꼴 영역을 정의 할 때 부채꼴 의위치는 충돌 검사를 수행하는 입자의 위치와 같게 설정하 였고, 부채꼴의 각도와 길이는 입자의 속도에 따라 자동으로 계산했다. 입자의 속도가 느린 경우는 부채꼴의 길이는 짧게 하고 각도는 넓게 설정하였다. 입자의 속도가 빠른 경우에는 이동 거리가 길기 때문에 부채꼴의 길이는 넓게각도는 좀 더 작게 설정하였고, 입자의 속도가 변하면 부채꼴 영역도 자동 으로 업데이트 되도록 하였다.

고정된 위치에서 충돌 검사를 수행하는 이전 기법들과 달리 본 연구에서는 입자의 속도에 따라 부채꼴 영역을 변화시켜 충돌 검사에 필요한 입자들의 개수를 줄이는 새로운 프레임워 크를 제안했다.2차원 입자 기반 시스템에서 수행한 결과 충돌 검사 성능이 2~3배 개선되었으며, 향후 인접 입자들의 정보를 매번 필요로 하는 3차원 입자 기반 유체 시뮬레이션에 적용하여 시뮬레이션성능을 고속화 할 수 있도록 연구할 계획이다.

감사의 글

본 연구는 2018학년도 강남대학교교내연구비 지원에 의해 수행되었음.

참고문헌

[1].

S. Premžoe, T. Tasdizen, J. Bigler, A. Lefohn, and R. T. Whitaker, “Particle-based simulation of fluids,” in Computer Graphics Forum, vol. 22, no. 3, 2003, pp. 401–410.

[2].

N. Sakamoto, J. Nonaka, K. Koyamada, and S. Tanaka, “Particle-based volume rendering,” in Visualization, 2007. APVIS’07. 2007 6th International Asia-Pacific Symposium on, 2007, pp. 129–132.

[3].

B. J. Lucchesi, “A parallel linear octree collision detection algorithm,” Ph.D. dissertation, University of Nevada, Reno, 2002.

[4].

D. R. Horn, J. Sugerman, M. Houston, and P. Hanrahan, “Interactive kd tree gpu raytracing,” in Proceedings of the 2007 symposium on Interactive 3D graphics and games, 2007, pp. 167–174.

[5].

S. Lefebvre and H. Hoppe, “Perfect spatial hashing,” in ACM Transactions on Graphics (TOG), vol. 25, no. 3, 2006, pp. 579–588.

[6].

J.-P. Heo, J.-K. Seong, D. Kim, M. A. Otaduy, J.-M. Hong, M. Tang, and S.-E. Yoon, “Fastcd: fracturing-aware stable collision detection,” in Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 2010, pp. 149–158.

[7].

T. Larsson and T. Akenine-Möller, “A dynamic bounding volume hierarchy for generalized collision detection,” Computers & Graphics, vol. 30, no. 3, pp. 450–459, 2006.

[8].

W. Fan, B. Wang, J.-C. Paul, and J. Sun, “An octree-based proxy for collision detection in large-scale particle systems,” Science China Information Sciences, vol. 56, no. 1, pp. 1–10, 2013.

[9].

T. Foley and J. Sugerman, “Kd-tree acceleration structures for a gpu raytracer,” in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, 2005, pp. 15–22.

[10].

S. Popov, J. Günther, H.-P. Seidel, and P. Slusallek, “Stackless kd-tree traversal for high performance gpu ray tracing,” in Computer Graphics Forum, vol. 26, no. 3, 2007, pp. 415–424.

[11].

S. Gottschalk, M. C. Lin, and D. Manocha, “Obbtree: A hierarchical structure for rapid interference detection,” in Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, 1996, pp. 171–180.

[12].

W. Zhao, C.-S. Chen, and L.-J. Li, “Parallel collision detection algorithm based on obb tree and mapreduce,” in International Conference on Technologies for E-Learning and Digital Entertainment, 2010, pp. 610–620.

[13].

M. Teschner, B. Heidelberger, M. Müller, D. Pomerantes, and M. H. Gross, “Optimized spatial hashing for collision detection of deformable objects,” in VMV: Proceedings of the Vision, Modeling, Visualization, vol. 3, 2003, pp. 47–54.

[14].

D. Knott and D. K. Pai, “Cinder: Collision and interference detection in real-time using graphics hardware,” in Graphics Interface, 2003.

[15].

N. K. Govindaraju, S. Redon, M. C. Lin, and D. Manocha, “Cullide: Interactive collision detection between complex models in large environments using graphics hardware,” in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware. Eurographics Association, 2003, pp. 25–32.

[16].

A. Greß and G. Zachmann, “Object-space interference detection on programmable graphics hardware,” in SIAM Conf. on Geometric Design and Computing, 2003, pp. 311–328.

[17].

N. K. Govindaraju, M. C. Lin, and D. Manocha, “Fast and reliable collision culling using graphics hardware,” IEEE Transactions on Visualization and Computer Graphics, vol. 12, no. 2, pp. 143–154, 2006.

[18].

C. Sigg, R. Peikert, and M. Gross, “Signed distance transform using graphics hardware,” in Proceedings of the 14th IEEE Visualization 2003 (VIS’03). IEEE Computer Society, 2003, p. 12.

[19].

P. Kipfer, M. Segal, and R. Westermann, “Uberflow: a gpu-based particle engine,” in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware. ACM, 2004, pp. 115–122.

[20].

A. Kolb, L. Latta, and C. Rezk-Salama, “Hardware-based simulation and collision detection for large particle systems,” in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, 2004, pp. 123–131.

[21].

K. E. Hoff III, J. Keyser, M. Lin, D. Manocha, and T. Culver, “Fast computation of generalized voronoi diagrams using graphics hardware,” in Proceedings of the 26th annual conference on Computer graphics and interactive techniques, 1999, pp. 277–286.

[22].

W. Chen, H. Wan, H. Zhang, H. Bao, and Q. Peng, “Interactive collision detection for complex and deformable models using programmable graphics hardware,” in Proceedings of the ACM symposium on Virtual reality software and technology, 2004, pp. 10–15.

[23].

N. K. Govindaraju, M. C. Lin, and D. Manocha, “Quick-cullide: Fast inter-and intra-object collision culling using graphics hardware,” in Virtual Reality, 2005. Proceedings. VR 2005. IEEE, 2005, pp. 59–66.

[24].

W. S.-K. Wong and G. Baciu, “Gpu-based intrinsic collision detection for deformable surfaces,” Computer Animation and Virtual Worlds, vol. 16, no. 3-4, pp. 153–161, 2005.

[25].

——, “Robust continuous collision detection for interactive deformable surfaces,” Computer Animation and Virtual Worlds, vol. 18, no. 3, pp. 179–192, 2007.