효과적인 뉴로피드백 훈련을위한 임계값 설정 기법

1. 서론

뉴로피드백(neurofeedback)은 피험자의 실시간 뇌파(electroencephalogram, 이하 EEG)를 분석하여 시각 또는 청각 형태의 피드백을 제공하는 뇌과학 분야의응용 기술이다. 뉴로피드백의 원리는 피험자의 두피에 뇌파 전극을 부착하여 뇌파를 측정하고, 특 정주파수 영역의 크기(진폭)가 임계값(threshold) 이상이 될 때, 피드백을 제공하여 해당 뇌파 성분이 활성화된 것을 피험자가 인지하도록 한다. 이와 같이 피험자가 자신의 뇌파 상태를 인지 하면서 특정 뇌파 성분을임계값 이상으로 활성화 시키는 훈련을 반복하면, 원하는 뇌파 성분을 능동적으로 제어할 수 있게 된다. 이러한 기술은 자율신경계나 중추신경계를 스스로 조절할 수 있 음을 보여주는 것으로 학습능력장애, 주의력결핍 과잉행동장애 (ADHD), 자폐증 등과같은 뇌신경계 질환의 치료나 개선을위 해 부작용이 없는 비침습적인(non-invasive) 치료법으로 꾸준히 연구되고 있다 [1, 2]

뉴로피드백은 기존의 약물 치료나 수술에 비해 효과가 즉각적이지 못하고, 훈련 콘텐츠 개발에 있어서도 해당 분야의 기술력과 임상 경험을 동시에 갖춘 개발자가 필요하기 때문에양질의 콘텐츠 개발이 쉽지 않다. 또한 시스템의 안정성과 효율성을 갖추기 위해 다양한 임상 실험을 통한 연구가 수반되어야 하는 어려움 을 갖는다. 그럼에도 불구하고, 뉴로피드백 훈련은 약물 치료에 비해 부작용이 거의 없고 효과 지속 시간이 길고, 학습에 있어서 매우 중요한 인지 수행 기능에 도움이 되는 등 다양한 분야로의 확장성이 크다는 장점이있다. Veron [3] 등은 지속적인임상 연 구와 기술 개발을 통해 다양한 훈련 프로토콜이 갖춰진다면 뉴로 피드백 훈련의 효과를 극대화할 수 있다고 주장하였다.

뉴로피드백 시스템에서 기본적으로 전제 되어야 하는 것은 정 확한 뇌파 신호의 획득이다. 신뢰도 높은 뇌파 신호를 얻기 위해서는 첫째, 두피 전극의 저항을 최소화해야 한다. Ferree [4] 등은 정밀한 디지털 필터와 고입력 임피던스 증폭기(high input impedance)를 사용하여 두피 전극의 저항을 최소화 하는 방법을 제안하였다. 둘째, 뇌파 측정시 발생할 수 있는 근육긴장(EMG), 안구운동(EOG)과같은 다른 생체 신호에 의해 유발되는 뇌파 잡 음(EEG artefact)을 제거해야 한다. 뉴로피드백의 경우 실시간으 로 뇌파 신호를 처리하여 피험자에게 피드백 하기 때문에 육안 검사를 통한 잡음 제거는 불가능 하고, 주로 IIR (infinite impulse response) 필터, FIR (finite impulse reponse) 필터 등의 디지털 신호 처리 기술을 사용한다.

뉴로피드백 시스템은 치료사가 사용하는 운영 SW와 피험자 의 훈련용 SW로 구분된다. 운영 SW는 피험자의 뇌파 진폭 값과 주파수 값을 실시간으로 확인하는 기능이있다. 환자의 실시간 뇌파 상태를 확인하여 보상 주파수(reward frequency)와 억제주 파수(inhibit frequency)의임계값을 조절함으로써 피험자의 훈련 상황을 통제한다. 임계값은 훈련 효과를 결정하는 매우 중요한 요소로 작용하는데, 치료사의임상 경험이 부족하여 잘못된 임계값이 설정될 경우 훈련 효과를 얻을 수 없게 된다. 일반적으로 훈련용 SW는 피험자의 뇌파 상태를 직관적으로 인지할 수 있도 록 간단한 기능성 게임(serious game)의 형태로 제공된다.

본 논문에서는 기존의 뉴로피드백 시스템에 비하여 효율적인 훈련을 지원하는 새로운 시스템을 개발하였다. 시스템은 뇌파 신 호를 추출하고 증폭하는 하드웨어와 증폭된 뇌파 신호의 잡음을 제거하고 분석하는 신호처리 모듈을 포함한다. 운영 SW는 치료 사가 설정한 임계값과 뇌파 신호의 분석값을 비교하여 긍정 피드 백과 부정 피드백을 생성하는 모듈과 훈련 효과를 극대화 하기 위 해서 임계값을자동으로 계산하는 기능을 담당한다. 훈련용 SW 는 운영 SW와 상호 연동을 통하여 긍정 피드백을 증가시키고, 부정 피드백을 감소시키는 기능성 게임 콘텐츠의 형태로 구성된다.

본 논문에서 개발된 뉴로피드백 시스템의 특징은 다음과같이 요약될 수 있다.

본 논문의 구성은 다음과같다. 제 2장에서는뉴로피드백 훈련과 관련된 이전 연구 및 임상 실험 결과를 소개하고, 제 3장에 서는 제안된 시스템에서 뇌파 신호를 획득하고 신호처리를 통해 파워스펙트럼 분석과 필터링 수행에 관한 부분을 설명한다. 제 4 장에서는 실시간으로 분석된 뇌파 신호에서 긍정 피드백과 부정 피드백을 생성하는 방법과 효과적 훈련을위해 임계값을자동으로 계산하는 방법에 대하여 설명한다. 제 5장에서는 개발 시스 템의자동 임계값 설정에 대한 실험 결과를 보이고, 끝으로 제 6 장에서는 본 논문의 결론과 향후 연구 방향을 제시한다.

2. 관련 연구

1929년 Hans Berger [5]가 최초로 인간의 뇌파를 측정한 이후, Kamiya와 Nowlis [6]는 피험자에게 알파파의 활동성을 말로 알려주면 피험자는 스스로 자신의 뇌파 상태를 통제 할 수 있다 는 것을 확인하였다. 뉴로피드백에서 사용되는 뇌파의 주파수 대역은 감각운동리듬(sensorimotor rhythm; 12 ~ 15Hz, 이하 SMR), 세타파(theta; 4 ~ 7Hz) 그리고 하이베타파(high beta; 22 ~ 36Hz) 등이다. Sterman과 Wyrwicka [7]은 고양이의 SMR 을 증가시키면 운동 활동성(motor activity)과경련이 감소된다는 사실을 발견하였고, 조작적조건화(operant conditioning)을 통해 서 고양이의 특정 뇌파를 증가시킬수 있음을 보였다.

뉴로피드백은 특정주파수 대역의 뇌파 활동성을 향상시키고, 동시에 다른 주파수 대역의 뇌파 활동을 억제하기 위해 설계되 었다 [8]. ADHD, 자폐증, 단순 틱장애 등의 정신 질환은 뇌파와 뇌파유발전위(ERP)의 왜곡 현상으로 설명될 수 있으며, 뉴로피드백은이러한 질환 치료 및 개선에 효과적이라는다양한 연구결과가 보고되었다 [9, 10, 11, 12, 13, 14, 15, 16, 17].

Sterman 등 [18] 은 간질환자를 대상으로 한 연구에서 대뇌 피 질의 체성감각중추 위치에 센서를 부착하고 SMR을 강화하는 뉴로피드백 훈련을 수행하였다. 훈련결과 이전에 화학 요법으로 통제되지 않았던 4명의 간질환자들의 발현이 감소되는 결과를 얻었다. Lubar 등 [8]은 ADHD의 경우 SMR의 강화와 세타파의 억제가 발작 또는 과잉행동성을 감소시킨다는 연구 결과를 발표 하였다. 뉴로피드백은 ADHD 치료에 효과적일 뿐만 아니라, 빠른 반응 시간, 공간 지각력 향상 등의 학습능력에도 영향을 준다. Michael 등 [19]은 SMR을 강화시키고, 세타파와 베타파의 비율을 안정화시키는 2가지 훈련 프로토콜을 사용하여 뉴로피드백 훈련을 수행하였다. 훈련결과 SMR 강화와 세타/베타 비율의 안 정화는 빠른 반응 및 공간 지각 능력과 관련된 운동에서 학습능력 향상에 도움이 된다는 실험 결과를 제시하였다 [20].

현재 세계적으로 많이 사용되고 있는뉴로피드백 시스템은 Procomp [21], EEGer [19] 그리고 Bioexplorer [22] 등이있다. Procomp [21]는 많은임상가들이 사용하며 8 채널까지지원이 가능하고 뉴로피드백 뿐만 아니라 바이오피드백 훈련까지 가능 지만, 사용법이 복잡한 단점이있다. EEGer [19]는 직관적이고 단 순한 사용법을 제공하지만, 훈련용 콘텐츠가 부족하고 확장성이 부족하다는 단점이있다. Bioexplorer [22]는 범용적인 바이오피드백 시스템을 지원하며, 주로 해당 분야의 개발자나 연구자에 의해 사용되고 있으나, 빌더의 형태이기 때문에 사용자 입장에서는 직관적 사용이 불편하다는 단점이있다.

본 논문에서 개발하는 시스템은 훈련 효과를 극대화하기 위해 보상 주파수나 억제주파수에 대한 임계값을자동으로 계산하는 기능을 제공한다. 기존 시스템에서는 임계값 설정을위해 뇌파 의 평균 진폭값을 더하거나 빼는 방법 [8], 뇌파의 평균 진폭값에 배수를 곱하는 방법 [23], 또는 일정 세션 동안 일정 범위의 강화 율을 유지하도록 임계값을 설정하는 방법 [24] 등이 사용되었으나, 이러한 기법들은 뇌파를 정현파로 근사하기 때문에 정확도가 떨어진다는 단점을 보인다. 본 논문에서 제안하는 기법은 피험자 의이전 뇌파의 패턴을 분석하여 설정된 목표 성공률을 보장하는 최적의임계값을 계산하는 기능을 지원한다.

3. 뇌파 신호의 획득 및 처리

최근 높은 정밀도를 갖는 뇌파 측정 기술들이 개발되어 뇌파 측정의 정확도 및 성능이 크게 향상 되었다. 본 논문에서는 뇌파 측정을위해 OpenEEG 모듈의 P2 통신 규약을 따르며 장시간 안 정적으로 2 채널뇌파 측정이 가능한 뉴런플렉스 [25]를 사용한 다. 뉴런플렉스는 10 비트로 표현된 0 ~ 1023 사이의 원시 데이터를 초당 256 개씩 측정하여 PC로 전송한다. 전송된 원시 데 이터는 변환 과정을 통해 −512 ~ +512µV 범위의 전위값으로 변환된다. 변환된 256개의 데이터는 32개씩 구분되어 8개의 패킷 (packet)에 담겨 신호처리 모듈로 전송된다.

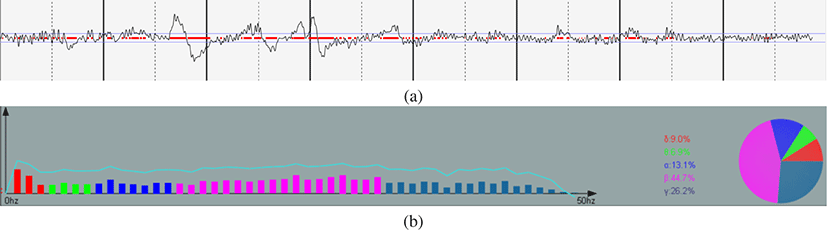
신호처리 모듈은 두 가지의 분석을 수행한다. 첫 번째로 실시 간 뇌파 신호의 FFT (fast Fourier transform) 변환을 통해 파워 스펙트럼(power spectrum) 분석 수행한다 [26]. 파워 스펙트럼 분 석은 시간 영역에서 측정된 뇌파 신호를 주파수 영역의 데이터 로 변환하여 각 주파수 진폭의 크기를 표시하는 분석 기법이다. 본 논문에서는 8초간 측정된 2048개의 원시 데이터에 FFT 변환 을 적용하여 0.125Hz 간격으로 0 ~ 128Hz 범위에서 진폭의 크기를 계산하여 파워 스펙트럼 분석을 수행한다. 그림 1(a)는 8 초 동안에 측정된 뇌파를 나타내며, 그림 1(b)는 분석된 뇌파 중 0 ~ 50Hz 범위에 포함된 델타, 세타, 알파, 베타, 감마파의 파워 스펙트럼 분석 결과를 나타낸다.

Figure 1: Real-time power spectrum analysis of brainwave signals (0 ~ 50Hz).

Download Original Figure

신호처리 모듈의 두 번째 기능은 훈련 주파수 범위에 해당하 는 뇌파 신호를 추출하기 위한필터링 기능이다. 이산 신호처리를 위한 디지털 필터는 주로 FIR (finite impulse response)과 IIR (infinite impulse response) 방식으로 구분된다. FIR 방식은 선형 phase를 갖는 특징이 있으며 영상 처리와 같은응용에 적합하지만, 뇌파와 같은 비선형 데이터의 처리에는 적합하지 않다. IIR 방식의 필터링 기법은이전 출력의 결과를 입력으로 이용하는 회 귀성을 포함하여, FIR 방식의 필터에 비해 낮은 차수로도 효율적 으로 필터링을 수행할 수 있는 장점이있다. 뉴로피드백 기술은 뇌파 신호에서 다른 생체 신호에 의한 잡음을 제거하고, 훈련 주 파수 범위의 신호를 추출하는 과정이 반드시 필요하다. 이를 위해 본 논문에서는 IIR 방식의 영역 통과(band pass) 필터를 이용하여 표 1과같은 주파수 범위의 뇌파 신호를 추출한다. 보상 주파수인 SMR을 추출하기 위해 본 논문에서 사용한 IIR 기반의 영역 통과 필터에 사용된 식은 다음과같다:

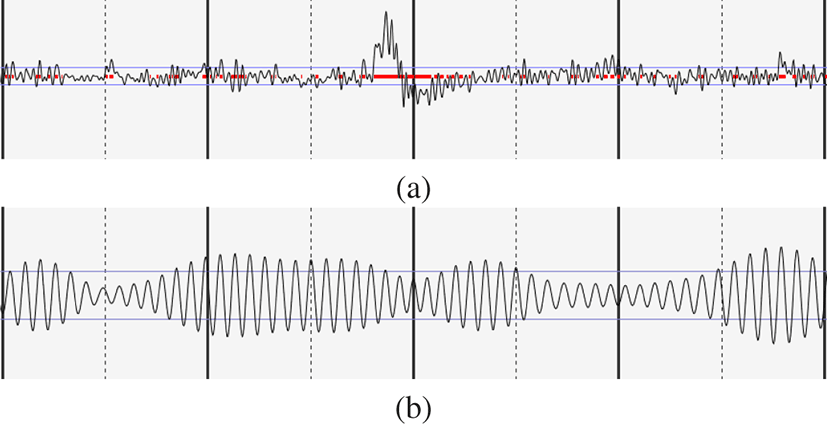
여기서 x[t]와 y[t]는 각각 시간 t에서의입력값과 출력값을 나타 내며, 필터의 계수는 Iowa Hills Filter Design 시스템 [27]과 타 원형 다항식(elliptical polynomial)을이용하여 실험적으로 결정 하였다. 그림 2(a)는 실시간 뇌파 신호를 나타내며, 그림 2(b)는 IIR 기반의 영역 통과 필터를 이용하여 추출된 SMR 신호를 나타낸다.

Figure 2: SMR brainwaves extracted by using a band pass filter: (a) real-time brainwaves, (b) extracted SMR (vertical scale is magnified for better visualization).

Download Original Figure

4. 자동 임계값 계산

4.1 피드백 생성

본 연구에서 제안하는뉴로피드백 시스템은 세타, SMR 그리고 하이베타 영역의 뇌파 신호를 분석하여 피험자에게 피드백을 제공한다(표 1). 세타와 하이베타의 신호는 억제주파수로서 해당 주파수의 진폭값이 치료사가 정한 임계값 이상일 경우 부정 피드백을 생성한다. 반면에 SMR은 보상 주파수이므로 해당 주파수의 진폭값이 치료사가 정한 임계값 이상일 경우 긍정 피드백을 생성 한다. 이러한 원리로 생성된 피드백은 게임의 형태로 제공되는 피험자의 훈련용 콘텐츠의입력으로 전달되어 게임의 진행 요소를 결정한다. 결국 피험자가 원하는 형태로 게임이 진행되도록 하기 위해서는 억제주파수인 세파와 하이베타의 진폭을임계값 이하로, 보상 주파수인 SMR의 진폭을임계값 이상으로 유지해야 한다. 피험자는 이러한 실시간 피드백 훈련을 통해 자신의 뇌파 상태를 스스로 조절하는능력을 습득하게 된다.

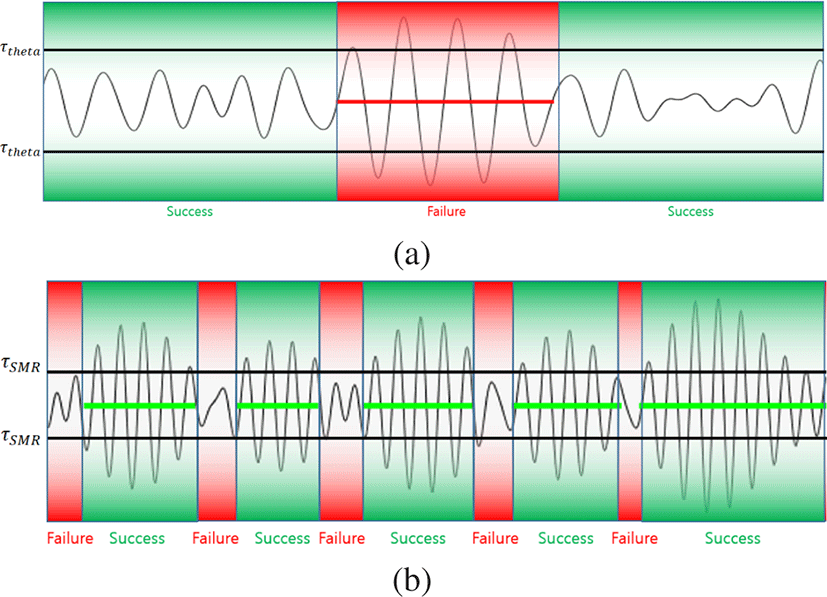
이러한 훈련 메커니즘의 핵심은 정확한피드백의 생성과 훈련 효과를 높이기 위한 정교한 임계값의 설정이다. 뇌파는 주기와 진폭을 갖는 진동파의 형태이기 때문에 주기 단위로 임계값과 비교해야 한다. 보상 주파수의 경우 뇌파 진폭값이임계값 이상인 경우에는 SUCCESS로 판단하고, 억제주파수의 경우 임계값 이상이면 FAIL로 판단한다. 판단 결과에 따라 SUCCESS인 경우 긍정 피드백을, FAIL인 경우 부정 피드백을 생성한다. 그림 3(a) 는 보상 주파수인 SMR에 대하여 주기를 고려하지 않고 임계값 이상인 신호들에 대하여 부분적으로 SUCCESS 구간을 판단한 잘못된 결과이다. 주기 단위로 SUCCESS/FAIL을 판단할 경우, 그림 3(b)와 같이 해당 구간 전체는 SUCCESS로 판단되어야 한 다. 뉴로 피드백의 훈련 주파수는 이산적인 값이 아닌 연속된 구 간의 형태로 정의된다. 가령, SMR의 경우 12 ~ 15Hz사이의 신호가 섞여 있기 때문에 시간 영역에서 신호의 진폭값과 임계값을 비교하는 것은 정확한피드백을 생성할 수 없다.

Figure 3: Judgement for SUCCESS section: (a) inaccurate result, (b) accurate result.

Download Original Figure

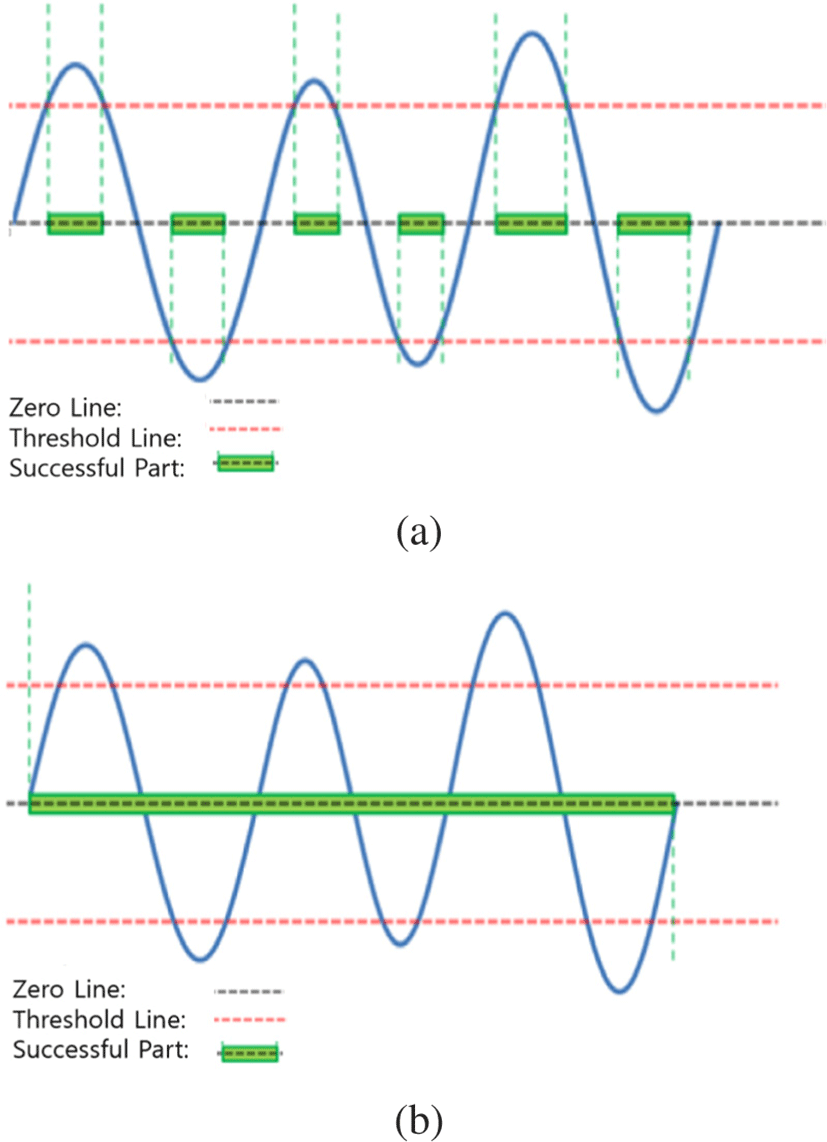
본 논문에서는 보다 정확한피드백 생성을위한 방법을 제시한다. 제시한 기법은 0.125초 마다 필터링된 뇌파신호에 FFT변환을 적용하여 분석된 뇌파신호의 파워 스펙트럼 값과 임계값과 비교 하여 SUCCESS 또는 FAIL을 판단한다. 뇌파 측정기가 초당 256 개(f_s=256)의 데이터를 샘플링 하므로 0.125초 마다 32개의 새로 운 데이터를 얻을 수 있다. 0.125초 동안 획득한 32개의 데이터에 대하여 FFT 변환을 적용할 경우 8Hz(f_d=256/32) 의 단위로 진폭 의 크기가계산되기 때문에 정확한 분석이 어렵게 된다. 본 논문 에서는 0.125초마다 새로 측정된 32개의 데이터와 이전 인터벌 (interval)에서 구한 32개의 데이터를 합쳐 64개의 데이터에 대한 FFT 변환을 적용하고, 4Hz 단위로 0 ~ 128Hz 사이의 진폭을 계산한다. SMR의 경우 다음 식과같이 해당 주파수 영역에서 파 워 스펙트럼 값의 합이임계값 이상을 경우 SUCCESS 피드백을 생성한다:

$$E={\displaystyle \sum _{k=12}^{15}{\left(f_k\right)}^2\ge {\tau }_{SMR},}$$

(2)

여기서 f_k는 주파수 k의 진폭값을 나타내고, τ_SMR는 SMR의임 계값을 나타낸다. 유사한 방법을이용하여억제주파수인 세타와 하이베타에 대해서도 피드백을 생성할 수 있다. 그림 4는 실시 간으로 필터링된 세타와 SMR에 대하여 위에서 제시한 방법을 이용하여 피드백을 생성한 결과이다. 주파수 영역에서 결정된 피드백과 시간 영역에서 보여지는 피드백의 결과가 일치하는 것을 확인 할 수 있다.

Figure 4: Judgment of SUCCESS/FAIL section: (a) theta wave, (b) SMR.

Download Original Figure

4.2 자동 임계값 계산

뉴로피드백 훈련이익숙하지 않은 피험자를 대상으로 보상 주파 수(SMR)의임계값을 너무 높게 설정한다면, 대부분 부정 피드 백이 생성되어 훈련 콘텐츠는 진행이 되지 않을 것이다. 반대로 보상 주파수의임계값을 너무 낮게 설정할 경우, 대부분 긍정 피드백이 생성되어 콘텐츠가 잘 진행되지만 피험자는 별다른 훈련 효과를 얻지 못하게 된다. 이러한 원리는 억제주파수에 대해서도 동일하게 적용될 수 있다. 따라서 훈련의 효과를 높이기 위해서는 피험자의 현재 상태를 명확히 파악하여 보상 주파수와 억제주파 수의임계값을 정교하게 조절하는 치료사의 역할이 매우 중요하 다. 본 논문에서 제안하는뉴로피드백 시스템은 치료사가 보상 주파수와 억제주파수에 대하여 목표 성공률을 설정하는 것을 지원한다. 시스템은 각각의 훈련 주파수에 대하여 일정시간 동안의 SUCCESS와 FAIL의 비율을 분석하고, 이를 이용하여 치료사가 목표하는 성공률을 얻을 수 있는 임계값을자동으로 계산한다. 현재 시간 t에서성공률(%) S_t를 다음과같이 정의할 수 있다:

$$S_t=\frac{N_S\times 0.125}{T}\times 100,$$

(3)

여기서 T는 성공률을 계산하는 일정시간(본 논문에서는 8초)을 나타내고, N_S는 8초 동안에 발생된 SUCCESS의 회수를 나타낸다. 상수 0.125는 SUCCESS가 0.125초 간격으로 결정되기 때문에 곱해진다.

치료사가 설정한 보상 주파수(SMR)에 대한 목표 성공률을 Ŝ 이라고 하자. 식 (3)로부터 현재 성공률이 Ŝ 이상이 되기 위해서는 이전 8초 동안에 발생된 성공의 횟수 N_S는 $\lceil \widehat{S}\times \frac{T}{0.125}\rceil$ 이상이 되어야 한다. 식 (2)을 통해 8초 동안 0.125초 간격으로 계산된

각각의 E_n, (n = 1, 2,…32)를 구하고, 이를 내림차순으로 다음 과같이 정렬한다:

$$E_1\ge \dots \ge E_{{\widehat{N}}_S}\ge E_{{\widehat{N}}_S+1}\ge \dots \ge E_{32}.$$

(4)

보상 주파수의 경우, 원하는 성공률 Ŝ를맞추기 위해서 임계값 τ_SMR = E_N̂S+1로 결정하면 SUCCESS의 수는 N̂_S가 되어 원하는 목표 성공률을 얻을 수 있다. 억제주파수의 경우, 반대로 오름차순으로 정렬하여 새로운 임계값을 E_N̂S+1로 결정하면목표 성공률을 얻게 된다

이러한 방법으로 계산된 임계값은 이전 8초 동안 발생한 뇌파가 이후 8초 동안에도 동일하게 반복된다는 가정하에 유효하다. 그러나 실제 훈련과정에서는 이전 8초와 동일한 뇌파가 반복되 지 않는다. 따라서 위의 방법으로 계산된 임계값이이후의 시간 에서 원하는 성공률을 보장할 수 없게 된다. 이러한 문제를 해결 하고 원하는 성공률에 근접한 최적의임계값을 구하기 위해서는 m개의이전 인터벌의 뇌파 데이터의 패턴을 모두 고려해야 한다. 본 논문에서는 이전 8개의인터벌(m = 8)을 모두 고려하여 최적의임계값을 구하는 기법을 제안한다. S_t−kT (τ)를 이전 k번째 인터벌에서 임계값 τ에 의해 결정되는 성공률이라고 하자. 원하는 성공률 Ŝ과 이전 8개의인터벌 시간 동안의 각각의 성공률 차이의 누적 함수는 다음과같이 정의될 수 있다:

$$E\left(\tau \right)={\displaystyle \sum _{k=1}^8{w}_k|\widehat{S}-S_t-k_T\left(\tau \right){|}^2,}$$

(5)

여기서 w_k는 이전 k-번째 인터벌에 대한 가중치이고 다음의 값을 사용하였다:

$$w_k=\left\{\frac{128}{255},\frac{64}{255},\frac{32}{255},\frac{16}{255},\frac{8}{255},\frac{4}{255},\frac{2}{255},\frac{1}{255}\right\}.$$

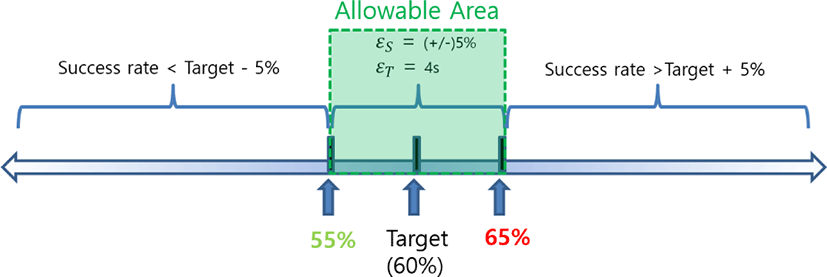
즉, 훈련 과정에서 피험자의 뇌파는 가장 최근 시간의 패턴이 반복될 가능성이 높기 때문에 본 논문에서는 가중치 값을이산 정규 분포를 적용하여 위와 같이 결정하였다. 식 (5)의 E(τ )를 최소화 하기 위해서 식 (4)에서 구한 임계값을 초기값 τ₀로 정하고, 수치적 최적화 기법 [28]을 이용하여 최적의 τ^*를 계산하였다. 이러한 최적의임계값은 매 순간계산되는 것이 아니고, 현재 성공률 S_t와 치료사가 지정한 성공률 Ŝ의 차이가 정해진 허용오차(ε_S)를 허용 시간(ε_T) 이상 벗어나는 경우에 한하여 임계값의자동 계산 이 수행된다. 그림 5은 성공률(Ŝ)을 60%로 지정하고, 허용오차 (ε_S = 5%), 허용 시간 (ε_T = 4초)로 설정한 경우를 도식화한 결과이다. 이러한 자동 임계값 계산 기능은 뉴로피드백 훈련에서 치료사의 역할을 보조하고, 훈련의 효율성을 높일 수 있는 중요한 핵심 기술이 된다.

Figure 5: Example of control parameters: target success rate (Ŝ = 60%), allowable error (ε_S = 5%) and time (ε_T = 4s).

Download Original Figure

4.3 상용 게임엔진과 연동

본 논문에서 제안한 뉴로피드백 시스템은 양질의 훈련 SW 콘텐츠를 쉽고 빠르게 제작하기 위해 상용 게임엔진인 unity3D와 연동 기술을 지원한다. 세타, SMR, 하이베타가갖는 긍정 피드백 과 부정 피드백의 조합에 따라 총 8가지 종류의 출력이 가능하다. 운영 SW는 생성된 피드백의 결과를 초당 8번씩 훈련용 콘텐츠에 UDP 방식으로 전송한다(그림 6). 이러한 기술은 기존 훈련용 콘 텐츠들이 제한적인 SDK를 이용하여 제작되는 한계를 극복하고, 개발자들이 게임엔진을이용하여 다양한 뉴로피드백 훈련 콘텐 츠를 제작하는 것을 가능하게 한다.

Figure 6: The output of FAIL (theta), SUCCESS (SMR) and FAIL (high beta) is transmitted to a training content through IPC module.

Download Original Figure

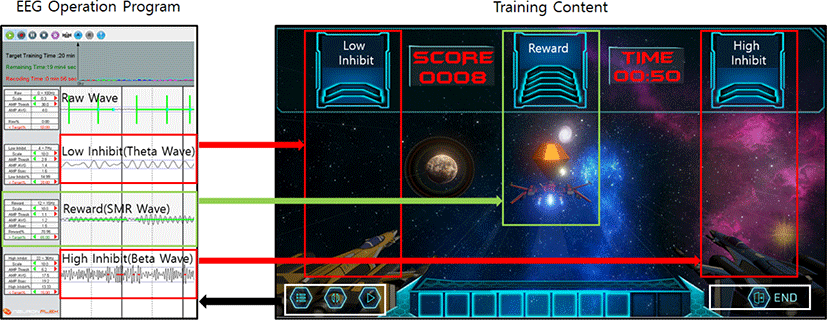
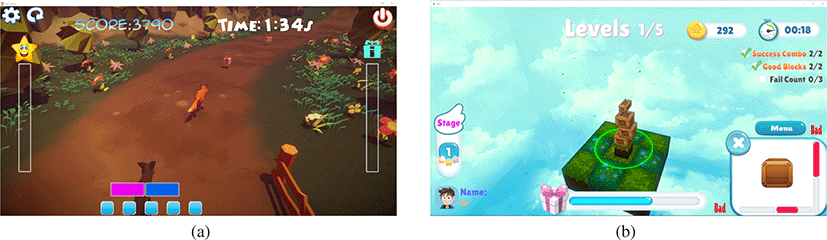
그림 6의 비행기 게임에서 SMR의 긍정 피드백은 중간 비행기의 속도를 높이게 된다. 반면에억제주파수의 부정 피드백은 좌우 비행기들의 속도를 높이거나, 게임의 배경화면을 어둡게 만 든다. 이러한 영향으로 훈련 과정에서 발생된 긍정 피드백은 게임 진행에 유리한 방향으로, 부정 피드백은 게임 진행을 방해하는 효과를 주어 피험자가 긍정 피드백을 높이는 방향으로 뇌파를 훈련시키게 된다. 그림 7는 unity3D 엔진을 사용하여 추가적으로 제작된 다양한 훈련 콘텐츠를 나타낸다. 그림 7(a)에서 긍정 피 드백은 여우 캐릭터의 달리는 속도를 증가시키고, 부정 피드백은 속도 감소와 화면을 어둡게 하는 효과를 준다. 그림 7(b)에서는 긍정 피드백은 상자의 크기를 크게하여 떨어지는 상자가 안정적으로 쌓일수 있도록 하는 반면, 부정 피드백은 상자의 크기를 줄여 상자가 쌓이는 것을 방해하는 효과를 준다.

Figure 7: Various training contents produced by interworking with commercial game engine.

Download Original Figure

5. 실험 결과

본 논문에서 제안한 자동 임계값 계산 알고리즘은 C++ 언어를 사용하여 Intel i7-4790 3.6 GHz CPU, 16 GB의 메인 메모리와 NVIDIA GeForce GTX770 그래픽 카드가 설치된 PC에서 구현 되었다. 제안된 기법의 성능을 평가하기 위해서 30대 성인 남성 3 명을 피험자로 선정하여 원시 뇌파 데이터를 10분간 측정하였다. 먼저 원시 데이터에 IIR 기반의 영역 통과 필터를 적용하여, SMR 영역의 뇌파 데이터를 추출하였다. 추출된 SMR에 대하여 임계값 τ_SMR = 3.5µV, 목표 성공률 Ŝ = 65%로 설정하여, 0.125 초 간격으로 SUCCESS 또는 FAIL의 피드백을 생성하여 전체 성 공률을 계산하였다. 또한 추출된 뇌파 데이터를 별도의 파일로 저장하여, 서로 다른 허용 시간과 허용오차에 대한 다양한 실험을 반복적으로 수행하였다.

표 2은 3명의 피험자 중에서 임의로 선정된 피험자의 실험 결과를 나타낸다. 첫 번째 행은자동 임계값 계산을 적용하지 않은 상태에서설정된 임계값에 대한 성공률을 나타낸다. 두번째 행은 동일한 초기 임계값에 대하여 목표 성공률을 65%로 설정하고, 성공률 오차 허용 범위를 ε_S = 10%이내 그리고 오차 허용 시간을 ε_T = 1초로 설정하고, 임계값 자동 계산을 통해 실험을 수행한 결과이다. 10분의 SMR데이터에 대하여 총 98번의 새로운 임계 값이자동으로 계산되었으며, 그 결과로 69.2%의 평균 성공률(표의 마지막 열)을 얻었다. 세 번째 행부터 다섯 번째 행까지는 동일 한 조건하에 허용오차를 점차 낮추어 실험을 수행한 결과이다. 허용오차가 낮아짐에 따라 임계값의 갱신 회수는 증가하는 것을 확인할 수 있으며 결과적으로 목표 성공률에 더 가까운 결과를 얻었다. 여섯 번째 행부터 여덟번째 행까지는 동일한허용오차에 대하여 허용 시간을 변화하여 임계값의 갱신 회수와 실제 성공률 을 측정한 결과를 나타낸다. 허용 시간이 늘어남에 따라 임계값 갱신의 회수는 줄어 들었으며목표 성공률과 다소 차이를 보이는 결과를 얻었다. 허용 시간이 6초인 경우(실험 8), 실제 평균 성공률(85.5%)은 목표 성공률(65%)의 허용오차 범위(60 − 70%)에 포함되지 못하는 결과를 얻었고, 이는 결국 허용오차 범위 밖의 데이터에 대하여 너무 긴 시간을 허용하여 실제로 충분한 회수의 임계값 갱신이 이루어지지 않았기 때문이다.

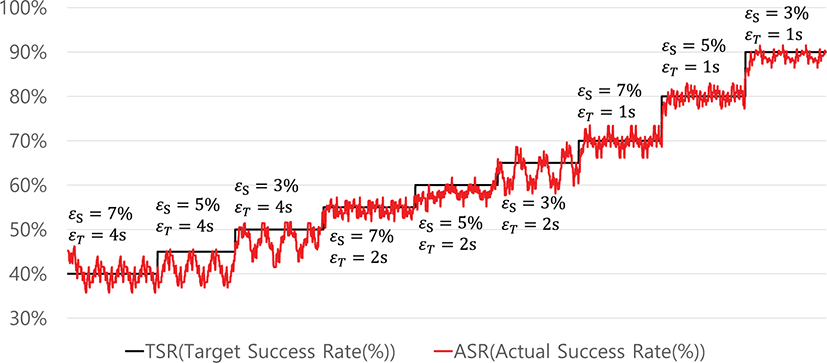
그림 8은 다양한 목표 성공률에 대하여 오차 허용 범위와오차 허용 시간을 달리 했을 때, 임계값 갱신의 회수와 실제 성공률을 그래프로 나타낸 결과이다. 각각 다른 목표 성공률, 오차 허용 범위 및 오차 허용 시간을 적용하여 실험을 진행하였다. 가로 축은 목표 성공률을 나타내며 세로 축은자동 임계값 방법에 의해 달성된 실제 성공률을 나타낸다. 그림 8(a)–(c)에서 오차 허용 시간은 ε_T = 1s로 설정되었으며, 각각 다른 오차 허용 범위 (ε_S = 3%, 5%, 7%)를 사용하여 성능을 측정했다. 검정색 선은 이상적인 사례(즉, 목표 성공률이 실제 성공률과같음)를 나타내 며 빨간색 선은 본 논문에서 제안한 방법을 사용하여얻은 실제 성공률을 나타낸다. 두 선 사이의 수직 거리는 지정된 조건에 대한 오류를 나타낸다. 그림 8(d)–(f) 및 그림 8(g)–(i)는 오차 허용 시간이 ε_T = 2s, 4s 이고 오차 허용 범위가 ε_S = 3%, 5%, 7%로 설정된 결과를 나타낸다.

Figure 8: Experimental results for SMR wave depending various experimental conditions.

Download Original Figure

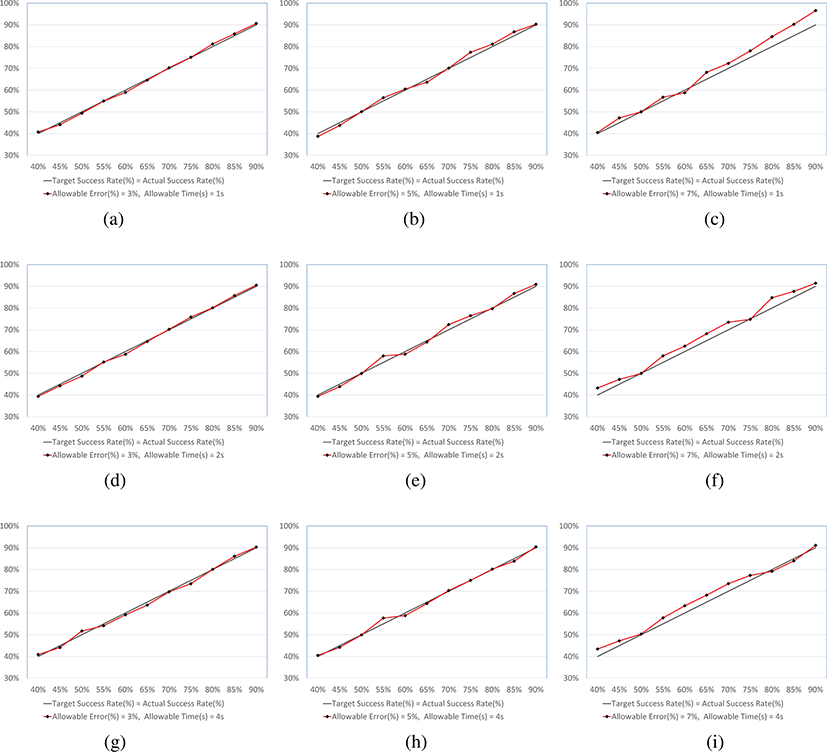
표 3는 치료사가 목표 성공률, 오차 허용 범위와오차 허용 시 간을 매 1분마다 변경하는다양한 유형의 실험에 따른 평균 성 공률의 결과를 보여주며, 그림 9는 표 3의 실험에서 실시간으로 변화하는 성공률을 가시화한 결과이다. 뇌파 데이터는 9분 동안 측정되며 가로 축과 세로 축은 각각 시간과 성공률을 나타낸다. 검정색 선은 치료사에 의해 지정된 목표 성공률을 나타내고, 빨간 색 선은 본 논문에서 제안한 자동 임계값 알고리즘에 의해 계산된 실시간 성공률을 나타낸다. 즉, 각 구간별 빨간색 선의 평균값이 표 3의 평균 성공률(마지막 열) 값에 대응된다.

Figure 9: Results for various target success rates changing in real time.

Download Original Figure

실험 결과를 통해 확인할 수 있듯이 본 논문에서 제안한 임계 값 자동 계산 기술은 피험자의 이전 뇌파패턴을 분석하여 목표 성공률에 가장 근접한 성공률을 얻을 수 있는 최적의 임계값을자 동으로 계산한다. 뉴로피드백 훈련에서 피험자가 적절한 수준의 긍정 피드백과 부정 피드백을 얻는 것은 훈련 결과에 많은 영향 을 준다. 이러한 상황에서 고정된 임계값을 사용할 경우, 피험자는 너무 높거나낮은 성공률을 얻게 되고, 결과적으로 좋은 훈련 효과를 얻지 못하게 될 것이다. 임계값 자동 설정 기술은이러한 문제점을 해결하기 위한 효과적인 방법으로 활용 될 수 있다.

6. 결론

본 논문에서는 효과적인 뉴로피드백 훈련을위한 시스템을 제안 하였다. 제안된 시스템은 치료사가 설정한 목표 성공률에 따라 자동으로 임계값을 조절하는 자동 임계값 설정 기능을 포함한다. 제안된 시스템은 설정된 임계값과 실시간 분석된 뇌파의 파워스 펙트럼 분석 값을 비교하여 0.125초 간격으로 정확한피드백을 생성한다. 생성된 긍정 피드백과 부정 피드백을 분석하여 일정 시간 동안의 성공률을 계산한다. 계산된 성공률이 치료사가 정한 목표 성공률의 오차 범위를 벗어날 경우, 시스템은 피험자의 이전 뇌파패턴을 분석하여 목표 성공률을 얻을 수 있는 최적화된 임계값을자동으로 계산한다. 본 논문에서는다양한 실험 결과를 통해서 효과적으로 목표 성공률과 일치된 임계값 계산이 가능하다는 것을 보였다. 이러한 임계값 자동 설정 기능은 뉴로피드백 훈련에서 훈련의 효과를 높일 수 있으며, 치료사와 피험자의 기 존 1:1 훈련 방식의 한계를 극복하여 다수의 피험자를 한 명의 치료사가 관리할 수 있도록 하여 훈련의 효율성을 높일 수 있을 것으로 기대된다.

현재 개발된 시스템을 활용하여 피험자들에 대한 실제 뉴로 피드백 훈련을 수행 중에 있으며, 향후 연구에서는 훈련 전/후에 대한 성과 분석을 통해 본 논문에서 제안한 임계값 자동 설정 기술의 실용성을입증하고, 한계점에 대한 보완 기술을 개발할 예정이다.