CNN을 이용한 Quad Tree 기반 2D Smoke Super-resolution

1. 서론

물리 기반 유체 시뮬레이션에서 해상도에 비례하여 연산량 이 많아지는 문제를 해결하는 것은 중요한 이슈 중 하나이 다. 시뮬레이션에서 해상도가 높아지면 연산량이 급격히 증 가하여 시뮬레이션 속도가 매우 느려지게 되는데, 최근에는 딥 러닝을 활용하여 이러한 문제를 해결하려는 연구가 진행 되고 있다. 딥 러닝을 활용하는 연구는 활용 부분에 따라 크게 두 가지로 나뉘게 된다. 첫 번째로 시뮬레이션 자체를 딥 러닝으로 풀어내려는 분야가 있다. 두 번째로는 시뮬레 이션 데이터를 입력 데이터로 하여, 스타일을 변경하거나 해상도를 높여 디테일을 표현하는 등의 연구 분야가 있다. 하지만 이런 연구들은 고해상도로 갈수록 데이터의 크기가 커지게 되어, GPU 메모리 부족으로 초고해상도의 데이터에 는 활용하기 어렵다. 또한, 전체 공간에 대하여 스타일을 변 경하거나 해상도를 높이므로, 불필요한 부분까지 연산하게 되어 전체 시뮬레이션이 비효율적일 수밖에 없다.

따라서 우리는 이런 문제들을 해결하기 위해 공간 분할법 중 하나인 쿼드 트리를 활용하여 Super-resolution을 효율 적으로 할 수 있는 기법을 제안한다. 본 논문에서 제안하는 기법을 이전의 기법들과 비교했을 때, 결과 차이는 없으면 서 Super-resolution이 필요 없는 부분의 연산이 줄어들어 시뮬레이션 속도가 향상되었다. 또한, 쿼드 트리를 활용하기 때문에 어떠한 해상도의 입력 데이터가 들어와도 공간을 분 할하여 연산을 진행하므로 초고해상도의 데이터에 대한 GPU 메모리 부족 문제도 해결하였다. 따라서 초고해상도의 데이터도 효율적인 Super-resolution이 가능하다. 앞으로 2 장에서는 딥 러닝 기반 유체 시뮬레이션과 공간 분할법, Super-resolution에 관한 관련 연구를 소개하고, 3장에서는 제안하는 알고리즘의 전체적인 과정을 설명한다. 4장에서는 본 논문의 기법에 대한 실험 및 분석 결과를 소개한 뒤, 결 론 및 향후 연구 방향을 5장에서 제시한다.

2. 관련 연구

유체 시뮬레이션과 딥 러닝을 결합하는 시도는 최근의 딥 러닝의 발전과 함께 많이 이루어지고 있다. 서론에서 이야 기했듯이 먼저 솔버 부분을 딥 러닝으로 해결하려는 연구가 있었는데, Tompson et al.[1]과 Xiao et al.[2]는 CNN을 사용 하여 Naiver-Stokes 방정식의 연산을 해결하는 기법을 제안 하였다. 다른 한편으로는 시뮬레이션 자체를 해결하는 것이 아닌 시뮬레이션 된 결과를 Super-resolution 하는 연구도 진행되었는데, Chu et al.[3]과 Xie et al.[4]은 2D 및 3D 연 기 시뮬레이션 데이터에 대해서 CNN과 GAN을 사용한 Super-resolution 기법을 제안하였다.

하지만 이런 연구들은 전체 데이터를 한 번에 연산하기 때 문에 GPU 메모리가 부족해지는 문제나 시뮬레이션이 비효 율적으로 연산 되는 문제가 있을 수 있다. 따라서 본 논문 에서는 이런 문제들을 해결하고자 쿼드 트리를 활용하여 2D 연기 밀도 데이터를 효율적으로 분할 하고 필요한 부분 만 Super-resolution 하는 기법을 제시하여 GPU 메모리 부족 문제를 해결하고, 전체 시뮬레이션을 가속화 한다.

딥 러닝을 활용한 Super-resolution은 이미지 영역에서 많 은 연구가 이루어지고 있는 분야이다. Dong et al.[5]은 처 음으로 Single Image Super-resolution을 딥 러닝 기반으 로 해결하는 기법을 제안하였고, 적대적 신경망(GAN)의 발 전과 함께 Christian et al.[6]은 적대적 신경망을 활용한 SRGAN을 제안하였다. 최근에는 Chu et al.[7]이 연속적인 이미지를 Super-resolution 하는 연구를 진행하였으며, CNN과 GAN을 활용한 이미지 Super-resolution 연구도 계 속 진행되고 있다[8].

공간 분할법 중에는 2D 공간과 3D 공간에서 효율적으로 사용할 수 있는 쿼드 트리[9]와 옥 트리[10]가 있다. 공간 분할법을 사용하는 것이 효율적인 이유는 원하지 않는 공간 은 집중하지 않고, 원하는 공간에 집중하여 연산할 수 있기 때문이다. Zhou et al.[11]은 GPU 기반 옥 트리를 활용하 여 3D 모델의 표면을 재구축하는 알고리즘을 제시하였다. 또한, 최근에는 공간 분할법과 딥 러닝을 함께 활용하는 연 구가 진행되고 있다. Gernot et al.[12]와 Wang et al.[13] 이 옥 트리와 CNN을 활용하여 3D 모델을 Classification과 Retrieval 및 Segmentation 하는 기법을 제안하였고, Maxim et al.[14]은 3D 모델을 생성하는 등의 공간 분할 법을 통해 메모리 문제와 속도 문제를 해결하는 연구를 진 행하였다. 하지만 이런 연구들은 유체 시뮬레이션보다는 모 델링과 렌더링에 초점을 두고 있다.

3. Method

본 논문에서 제안하는 알고리즘은 크게 3가지 과정으로 구 성된다. 첫 번째는 쿼드 트리를 활용하여 Super-resolution 이 필요한 영역을 분류하는 전처리 과정이다. 다음으로 두 번째는 저해상도의 데이터와 고해상도의 데이터를 학습 데 이터로 하여 CNN 기반의 Super-resolution 모델을 학습한 뒤, 전처리 과정을 거친 데이터를 학습된 모델에 넣어 고해 상도의 데이터로 변환하는 Super-resolution 과정이다. 마지 막으로 변환된 여러 고해상도 데이터를 하나의 데이터로 만 들어주는 후처리 과정이 있다.

3.1 쿼드 트리를 활용한 전처리

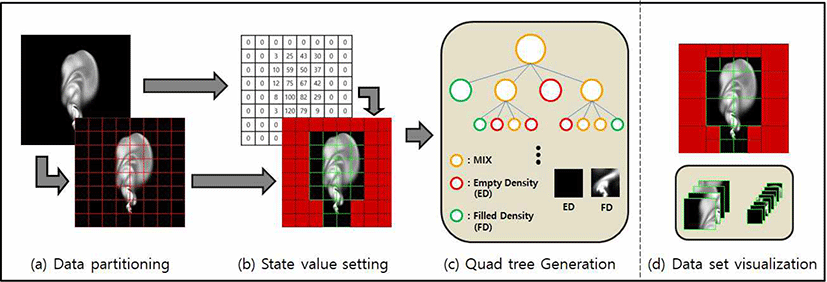
공간 분할법 중 쿼드 트리는 2차원 데이터를 분할 하기에 적합한 알고리즘 중 하나이다. 본 논문에서 제안하는 쿼드 트리를 활용한 전처리 과정은 먼저 입력된 밀도 데이터를 임의의 패치 크기에 맞게 분할 하고(Figure 1a), GPU를 활 용한 병렬 연산을 통해 각 패치 데이터의 최댓값으로 구성 된 행렬을 생성한다. 생성된 최댓값 행렬을 가지고 분할된 패치의 Super-resolution 필요 유무를 상태 값으로 결정하게 되며(Figure 1b), 각각의 패치가 최하층 노드가 되어 상태 값과 노드에 관한 정보를 가지고 Bottom-Up 방식으로 트리 구조를 생성하게 된다(Figure 1c). 마지막으로, 생성된 쿼드 트리를 통해 Super-resolution이 필요한 공간의 데이터를 추 출하게 되는데, 가시화하면 Figure 1d와 같다.

Figure 1. Pre-process using space partitioning method

Download Original Figure

3.1.1 패치의 상태 값

패치의 상태 값은 쿼드 트리 생성에 중요한 역할을 하게 되 는데, 상태 값은 패치별 Super-resolution 필요 유무를 의 미하고 다음과 같이 정의된다.

먼저 시뮬레이션 공간을 미리 정의한 크기의 패치로 분할 하고, 각 패치에서의 최댓값이 임의로 정한 임곗값보다 크 면 해당 패치는 Super-resolution이 필요한 공간이라고 판 단하여 상태 값을 Filled Density 즉 “FD”로 정의하였다. 반 대로, 임곗값보다 작은 경우에는 Super-resolution이 필요 하지 않다고 판단하여 상태를 Empty Density 즉 “ED”로 정의하였다. 따라서 상태 값이 FD라면 Super-resolution을 수행하고, ED라면 Super-resolution을 수행하지 않는다. 본 논문에서는 임곗값을 0.01로 두었다.

Figure 2. GPU based maximum value matrix calculation

Download Original Figure

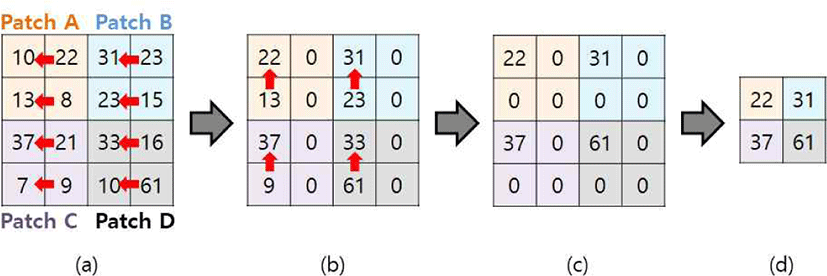
각 패치의 최댓값을 구하는 기법은 다음과 같다. 예를 들 어 Figure 2와 같은 4x4의 데이터가 있을 때, 패치 크기를 2x2로 설정하면 전체 시뮬레이션 공간은 크기가 2x2인 4 개의 패치로 분할된다(Figure 2a). 이때 전체 데이터를 GPU 기반 병렬 연산을 통해 Reduction을 하면서 최댓값을 찾아가다 보면(Figure 2b, c), 결과로 나온 2x2의 행렬이 각 패치의 최댓값 모음이 되는 것을 알 수 있다. 이렇게 나 온 최댓값 행렬을 가지고 임곗값과 비교하여 각 패치의 상 태 값을 결정한다. 이와 다르게 최댓값을 찾을 때, 패치의 모든 데이터를 차례로 순회하며 찾는 CPU 기반의 기법도 있다. 본 논문에서 제시하는 GPU 기반 기법과 CPU 기법 간의 속도 차이를 알아보기 위해 4장에서 비교 실험을 진 행하였다.

3.1.2 쿼드 트리 생성

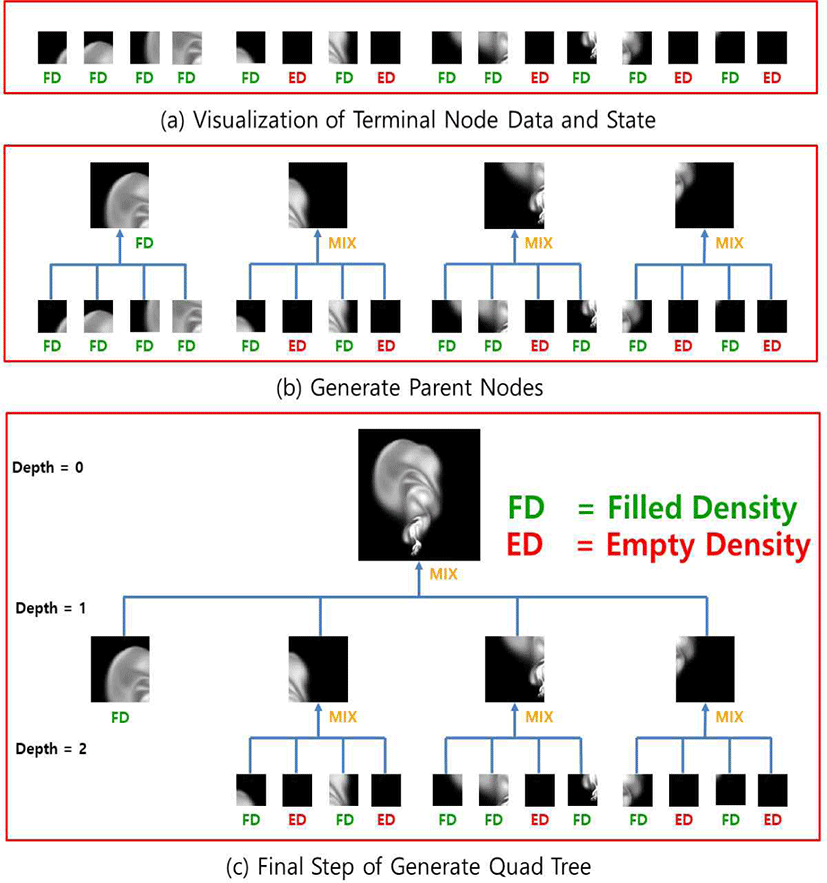
쿼드 트리는 전체 시뮬레이션 공간을 미리 정의한 패치 크 기로 분할한 각각의 패치 데이터와 앞서 계산한 패치에 해 당하는 상태 값을 가지고 최하단 노드를 만들고(Figure 4a), 그 노드들을 기반으로 쿼드 트리를 Bottom-Up 방식 으로 구성한다.

Figure 3. Each node information

Download Original Figure

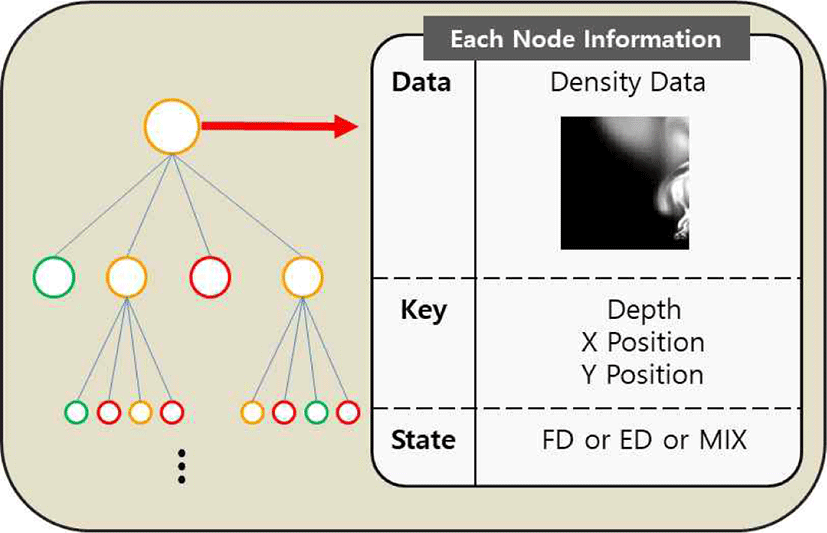
쿼드 트리의 각 노드는 데이터, 키, 상태 값을 갖는다 (Figure 3). 먼저 데이터값은 그 노드에 해당하는 밀도 데이 터이다. 다음으로 키값은 (깊이, x_좌표, y_좌표)로 구성되어 있다. 깊이는 쿼드 트리를 만들 때, 최상위 노드의 깊이를 0 으로 설정하고 최상위 노드의 자식 노드부터 깊이가 1씩 증 가하는 구조이다(Figure 4c). 전체 데이터 크기와 깊이를 알 게 되면 본 논문에서 제안하는 쿼드 트리 특성상 깊이가 1 깊어질수록 크기가 0.5배 되므로 현재 노드의 데이터가 어 떤 크기를 가졌는지 알 수 있게 된다. x_좌표와 y_좌표는 각각의 노드가 가진 데이터가 전체 데이터에서 위치한 좌표 를 저장하는데, 깊이와 좌푯값은 나중에 Super-resolution 과정이 완료된 뒤 후처리 과정에서 필요하게 된다. 3.1.1에 서 정의한 상태 값은 쿼드 트리 구성 중에 FD, ED 이외에 도 MIX 값을 가질 수 있는데, 이는 이 항목의 후반부에 자 세히 설명하도록 한다.

Figure 4a를 보면 각 패치의 밀도 데이터를 최하단 노드의 데이터로 설정해 주었다. 최하단 노드가 가진 키값의 깊이 는 수식 (1)처럼 구할 수 있다. 여기서 d 는 현재 노드의 깊이가 되고，D_width 는 전체 입력 데이터의 너비 값， N_width 는 현재 노드 데이터의 너비 값이 된다.

$$d={\log }_2\left(D_{width}/N_{width}\right)$$

(1)

그다음 노드를 4개씩 모아서 부모 노드를 생성하게 되는 데 (Figure 4b), 부모 노드의 데이터는 자식 노드 4개의 데 이터를 합친 것이 되고, 키값의 깊이는 1 줄어들게 되고, x_좌표와 y_좌표는 자식 노드 중 제일 작은 값을 가지게 된다. 마지막으로 상태 값은 자식 노드들의 상태 값을 확인 하여 Table 1과 같이 결정되게 된다.

Table 1. The state of the parent node is decided according to the state of the child node

Child node state value	Parent node state value
All child node is FD	FD
All child node is ED	ED
Three state are mixed	MIX

Download Excel Table

또한, 만약 자식 노드 4개의 상태 값이 전부 “FD” 또는 “ED”라면 자식 노드를 삭제하게 된다. 왜냐하면 “FD”의 경 우 자식 노드의 상태 값이 전부 같으므로 자식 노드 4개를 각각 연산하는 것보다 부모 노드에서 한 번에 연산하는 것 이 결과가 같으면서 속도가 더 빠르기 때문이고, “ED”라면 Super-resolution을 할 필요가 없기 때문이다. 이 작업을 깊이가 0이 될 때까지 반복하게 되면 Figure 4c에서 보이 는 것처럼 최종 쿼드 트리가 생성된다.

쿼드 트리가 생성되면 깊이가 0인 최상단 노드에서부터 상태 값을 확인하며 모든 “FD”인 노드의 데이터와 키값을 모은다. 상태 값이 “ED”라면 Super-resolution이 필요하지 않은 공간이므로 버린다. 마지막 노드까지 탐색을 마친 뒤 모아둔 데이터를 Super-resolution 입력 데이터로 사용한 다.

Figure 4. Generate Quad Tree.

Download Original Figure

3.2 Super-resolution

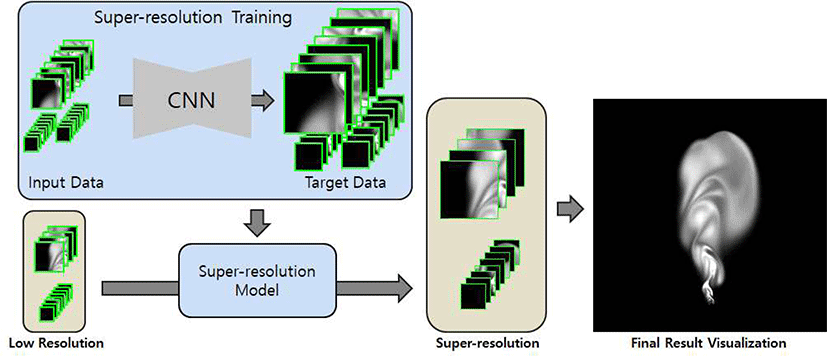
Super-resolution은 학습과 사용 두 단계로 나뉜다. 첫 번 째로 학습 단계에서는 Figure 5의 왼쪽 위에서 보이는 것과 같이 입력 데이터인 저해상도 데이터와 표적 데이터인 고해 상도 데이터로 구성된 학습 데이터가 필요하다. 학습 데이 터를 생성하는 과정은 다음과 같다.

먼저 2D 연기 시뮬레이션 데이터를 얻기 위해 512x512 해상도의 격자 기반 연기 시뮬레이션을 수행하여 임의의 5 가지 장면을 300프레임씩, 총 1500프레임의 2D 연기 시뮬 레이션 데이터를 생성하였다. 본 논문에서는 Stam의 Stable Fluids[15]를 사용하였다. 생성한 데이터를 가지고 패치 크 기 16x16으로 쿼드 트리를 만들어 상태 값이 “FD”인 데이 터만 모아서 학습용 표적 데이터를 구성하였다. 학습용 입 력 데이터는 표적 데이터를 Blur 처리한 뒤 Resize를 하여 Down Sampling 된 저해상도의 데이터로 구성하였다.

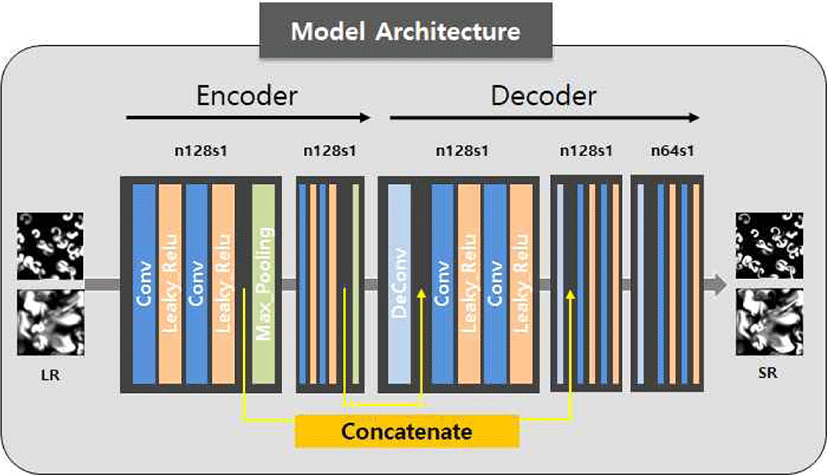
다음으로 Super-resolution을 하는 모델을 구성하였다. 모 델은 다음 Figure 6과 같이 구성되어 있다. Figure 6에서 LR은 저해상도의 데이터(Low Resolution), SR은 Super-resolution 된 데이터, n은 필터의 개수, s는 Stride 크기를 나타낸다. 하나의 Convolution Layer는 3x3 크기의 Convolution 필터와 Activation Function인 Leaky Relu를 2 개씩 사용하였고, 인코더에서의 Pooling은 Max Pooling을 사용하였으며, 디코더에서는 Deconvolution을 통하여 Convolution Layer를 구성하였다. Convolution Layer를 Figure 6과 같이 쌓아서 전체 모델을 구성하였고, 중간에 크 기가 같은 앞의 Activation Map과 뒤의 Activation Map을 He et al.[16]이 제안한 Skip Connection으로 연결하여, 이전 의 정보를 잃지 않도록 구성하였다.

Figure 5. Super-resolution and Post-processing

Download Original Figure

Figure 6. Model Architecture

Download Original Figure

이 모델로 학습을 진행하면서 사용한 Loss Function은 Mean Squared Error(MSE)를 사용하였고， 식은 (2) 와 같다.

$$L=\frac{1}{W\times H}{\displaystyle \sum _i^W{\displaystyle \sum _j^H{\left(S{R}_{ij}-H{R}_{ij}\right)}^2}}$$

(2)

여기서 L 은 Loss Function올 의미하고，W, H는 각각 전 처리 된 데이터의 너비와 높이를 의미한다. SR, HR은 Super-resolution 된 데 이 터와 표적 데 이 터 인，고해 상도의 데이터이다. Optimizer는 Adam을 사용하였고，Learning rate 는 0.0001，배치 크기는 512로 두고 총 50 epoch의 학습을 진행하였다.

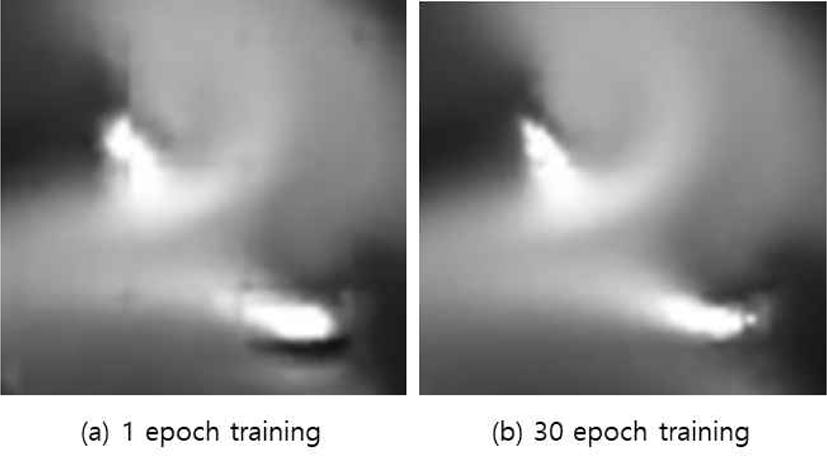
학습 과정에서 Figure 7을 보면 입력 데이터에는 없고, 표적 데이터에는 있는 디테일한 부분들이 살아나는 것을 확 인할 수 있었다.

Figure 7. Visualization of several training epoch

Download Original Figure

사용 단계에서는 학습이 완료된 모델에 쿼드 트리를 이용 한 전처리에서 생성된 데이터를 입력으로 넣어주면, Super-resolution이 완료된 고해상도의 데이터를 얻을 수 있다.

3.3 데이터 후처리 과정

마지막으로 앞에서 얻은 고해상도의 데이터들을 후처리 작 업으로 하나로 모아주어 최종 데이터를 만들어낸다. 3.1.2 에서는 쿼드 트리를 생성할 때 각각의 노드가 데이터와 키 값을 저장했었다. 키값은 깊이와 x, y 좌표를 갖고 있으므 로 해당 노드의 패치 크기와 위치를 특정할 수 있다. 이러 한 특징을 이용하여 여러 크기로 나누어진 패치 데이터를 하나로 모아주는 작업이 가능하다.

먼저 0으로 채워진 표적 데이터 해상도의 공간을 만들고, Super-resolution 된 고해상도의 데이터들을 키값에 있는 깊이와 x,y 좌표를 가지고 각각의 공간에 맞게 모으면 나머 지 공간은 자연스럽게 0으로 채워진 상태 값이 “ED” 였던 데이터들의 공간이 된다. 본 논문에서 제시한 기법은 학습 이 적게 되었을 때 후처리 작업을 하게 되면, Figure 8a에 서 보이는 것과 같이 패치와 패치 사이의 경계 부분에서 Artifact가 생기는 것을 확인하였다. 하지만 이는 모델이 학 습을 계속 진행함에 따라 해결됨을 확인할 수 있었다 (Figure 8b).

Figure 8. Visualization of boundary problem.

Download Original Figure

4. 실험 및 분석

본 논문에서 제안하는 기법을 실험 및 분석해보기 위해 여 러 가지 다른 기법들과 비교해보았다. 먼저 본 논문에서 제 안하는 기법은 다음과 같은 환경에서 구현되었다. Intel Core i7 8700K CPU, 16GB RAM, GTX 1080 8GB 그래 픽 카드를 사용하였고 Stam의 Stable Fluids[15] 를 2D 연 기 시뮬레이션 데이터로 사용하였다. 실험 데이터는 Figure 5에서 가장 우측에 나오는 것과 같은 기본적인 장면의 데 이터를 사용하였다.

실험 및 분석은 크게 두 가지로 나뉘는데, 첫 번째로 모델 을 통해 나온 고해상도 데이터가 디테일한 부분을 표현하면 서 표적 데이터와 유사한지 실험하였다. 두 번째는 속도 비 교로 총 4가지 기법을 비교하였는데. 첫 번째로 Whole SR(Super-resolution)은 입력으로 받은 전체 데이터를 통째 로 Super-resolution 하는 것이다. 이 기법은 이전 연구들이 사용했던 기법으로써 해상도가 커지면 GPU 메모리 문제가 생겨서 대용량의 데이터에서는 결과를 확인할 수 없다 (Figure 11 bottom). 두 번째는 Patch SR이다. 이 기법은 임 의의 패치 크기로 데이터를 분할 한 뒤, 쿼드 트리를 생성 하는 것이 아니라 분할된 패치 데이터를 입력 데이터로 Super-resolution을 진행한 것이다. 세 번째와 네 번째 기법 은 둘 다 쿼드 트리를 사용하고 각각의 상태 값을 통해 Super-resolution을 진행하는 방식은 같지만, 다른 점은 최 하단 노드의 상태 값 결정 방식을 CPU 기반 데이터 순회 방식으로 했는지, 아니면 본 논문에서 제안하는 GPU 기반 병렬 처리 방식으로 했는지의 차이이다. SR with CPU Quad Tree는 CPU 기반 데이터 순회 방식이고, SR with GPU Quad Tree는 GPU 기반 병렬 처리 방식이다.

4.1 Super-resolution

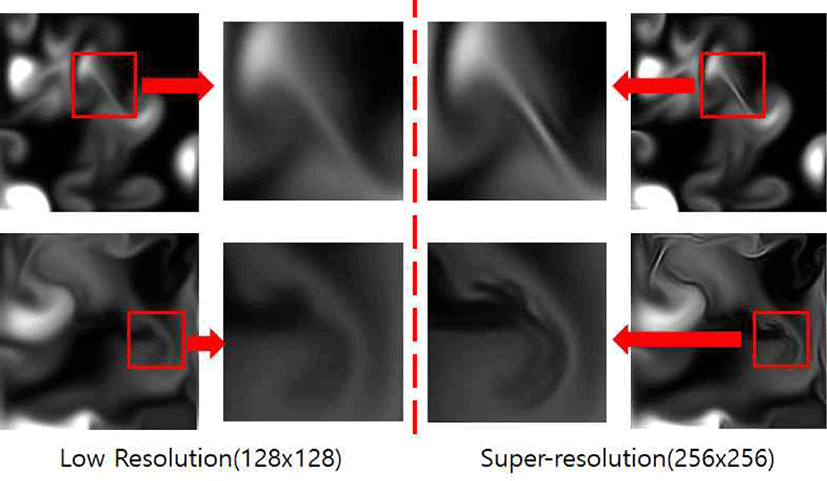
먼저 제안하는 모델이 만든 Super-resolution 결과를 비교해 보았다. 초고해상도 데이터는 세부적인 결과들이 논문의 Figure로는 표현이 되지 않아서 저해상도의 입력 데이터로 실험을 진행하였다. Figure 9를 보면 저해상도(128x128)의 입력 데이터를 본 논문에서 제안하는 모델에 넣어 줬을 때, Super-resolution 후에 고해상도(256x256)가 되어 나온 결과 가 디테일한 부분을 표현하면서 표적 데이터와 유사한 것을 확인하였다.

Figure 9. Super-resolution result

Download Original Figure

4.2 속도 비교

4.2.1 CPU, GPU 기반 상태 값 결정 속도 비교

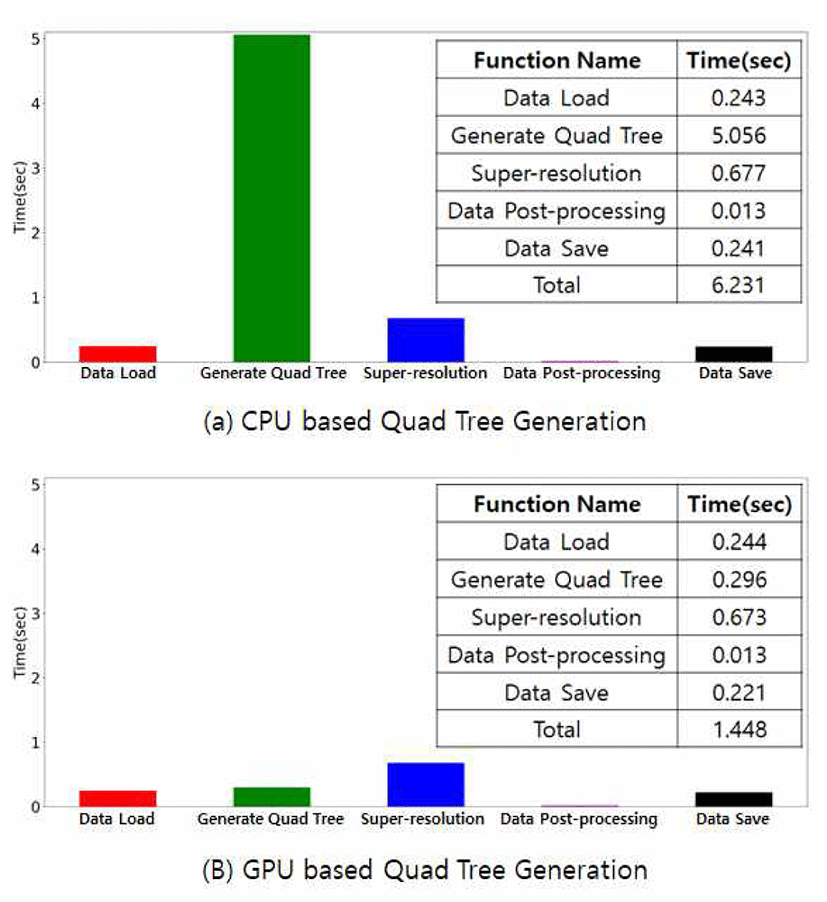
본 논문에서 제안한 GPU 기반 병렬 연산을 통한 상태 값 결정과 CPU 기반 데이터 순회 상태 값 결정에 대한 속도 비교는 Figure 10과 같다. x축은 전체 알고리즘의 각 함수 의 이름이고, y축은 각 함수의 소요 시간을 표현하였다. 빨 간색은 데이터 로드, 초록색은 쿼드 트리 생성, 파란색은 Super-resolution, 분홍색은 데이터 후처리, 마지막으로 검 은색은 데이터 저장에 걸린 시간을 표현하였다. 상태 값 결 정은 쿼드 트리 생성함수 안에 포함되어있다. 결과를 보면 입력 해상도로 2048 x 2048 크기의 밀도 데이터를 사용하 였는데, 다른 함수들의 소요 시간은 거의 일정하였으나 쿼 드 트리 생성함수가 CPU 기반일 경우에는 5.056초, GPU 기반일 경우에는 0.296초로 GPU 기반일 때 약 17배 정도 빨라지는 것을 확인할 수 있었다. 또 전체 과정에 소요된 시간은 쿼드 트리 생성이 CPU 기반일 경우 6.231초, GPU 기반일 경우에는 1.448초로 약 4.3배 정도 빨라지는 것을 확인할 수 있었다.

Figure 10. Result of the function running time for input resolution 2048 x 2048

Download Original Figure

4.2.2 패치 크기에 따른 속도 비교

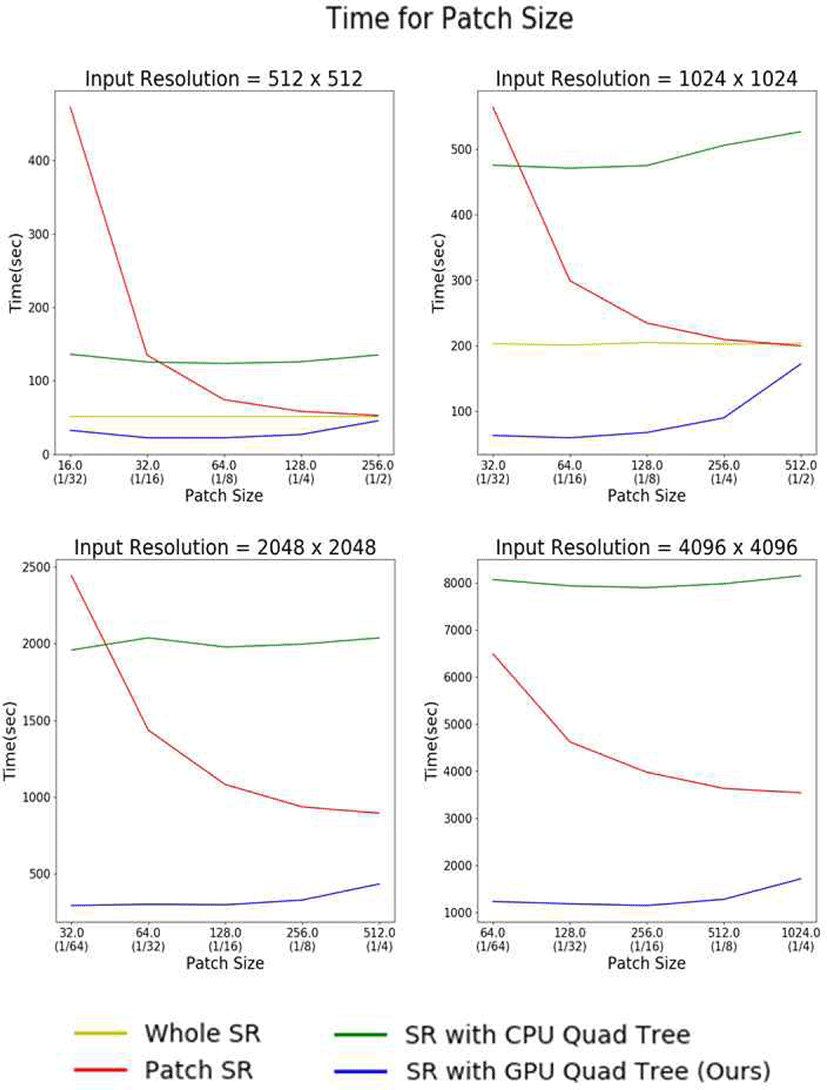
다음은 본 논문에서 제안하는 기법을 활용하여 여러 가지 입력 해상도와 패치 크기를 가지고 2D 연기 시뮬레이션을 Super-resolution 하는 실험을 진행하였다. Figure 11에서 볼 수 있듯, 총 4가지의 입력 해상도에서 5가지 패치 크기 를 비교하였다. Figure 11의 결과를 보면 입력 해상도와 무 관하게 모두 본 논문이 제안하는 기법이 가장 빠른 것을 알 수 있다. 하단의 두 결과에서 Whole SR이 없는 이유는 입 력 해상도가 2048 x 2048 이상인 데이터에서는 GPU 메모 리 문제로 인해 Super-resolution이 불가능하였기 때문이 다. CPU, GPU 기반 상태 값 결정에서 비교 실험한 것과 같이 쿼드 트리를 생성할 때 CPU 순회 방식을 사용하는 것 은 GPU 병렬 처리를 사용한 것보다 느릴 뿐만 아니라, Whole SR 방식보다도 느리고, 일정 패치 크기에서는 Patch SR보다도 느린 것을 확인할 수 있었다. 또 패치 크기에 따 라서는 Patch SR은 패치 크기가 작아지면 작아질수록 걸리 는 시간이 급증하는 것을 확인할 수 있었다. 또한, 쿼드 트 리를 사용했을 시에는 최하단 노드의 패치 크기를 무조건 작게 하는 것이 항상 속도가 빨라지는 것이 아님을 확인하 였고, 패치 크기를 입력 해상도의 16분의 1 크기로 했을 때 속도가 가장 빠른 것을 확인하였다.

Figure 11. Result of the running time for several input resolutions and patch sizes

Download Original Figure

4.2.3 입력 해상도에 따른 속도 비교

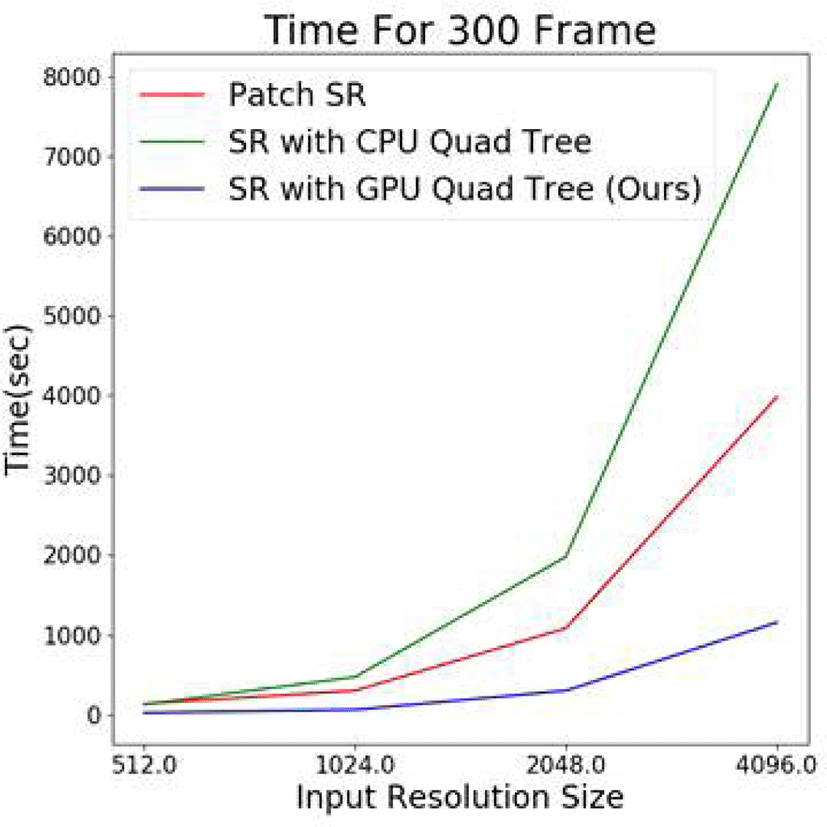
마지막으로 Figure 12는 입력 해상도를 다르게 했을 때, 300프레임의 데이터를 Patch SR과 CPU 버전의 쿼드 트리, 본 논문이 제안하는 GPU 버전의 쿼드 트리 방식을 비교해 본 결과이다. 패치 크기는 각각의 기법에서 가장 속도가 빠 른 크기로 하였다. 입력 해상도의 크기가 커짐에 따른 시간 의 기울기가 본 논문에서 제안하는 방식이 제일 작은 것으 로 보아 해상도가 계속 커져도 본 논문에서 제안하는 기법 이 가장 속도가 빠르다는 것을 유추해 볼 수 있었다.

Figure 12. Result of the running time for different input resolutions

Download Original Figure

5. 결론

우리는 본 논문에서 2D 연기 시뮬레이션을 쿼드 트리와 Super-resolution을 통해 가속화 하고 메모리를 효율적으로 사용하는 기법을 제안하였다. 분할된 패치와 상태 값을 기 반으로 쿼드 트리를 생성하였으며, 생성된 쿼드 트리를 사 용하여 Super-resolution이 필요한 공간을 분할 및 분류하 고, Super-resolution과 후처리를 통해 결과 데이터까지 얻 을 수 있는 기법을 제안하였다.

실험을 통해 알 수 있었던 사실은 각각 나눠진 패치의 Super-resolution의 필요 유무를 확인할 때, CPU를 활용하 는 것보다 GPU를 활용하는 것이 훨씬 큰 폭으로 속도가 향상된다는 것이다. 또한, 이 기법을 통해 이전 기법들의 입 력 해상도의 크기에 따른 GPU 메모리 부족 문제를 해결하 였고, Super-resolution을 필요한 공간에만 진행함으로써 전 체 시뮬레이션 속도가 향상되었음을 확인할 수 있었다. 하 지만 입력 데이터의 해상도에 따른 적합한 패치 크기는 현 재 실험을 통해서만 확인할 수 있는 한계점을 가지고 있다. 적합한 패치 크기를 자동으로 찾을 수 있다면 더 효율적인 기법이 될 것이다.

향후 3D 연기 시뮬레이션 데이터에서도 본 논문이 제시하 는 기법이 적용되는지 옥 트리를 활용하여 확인할 것이다. 또한，제안하는 기법을 다른 기법에도 적용해 보기 위하여 Sato et al.[17]이 제안한 Style Transfer나， Xie et al.[12]이 제안한 GAN을 활용한 Super-resolution 등의 공간 을 활용한 여러 가지 기법에도 적용해 볼 것이다.