1. 서론
캐릭터 애니메이션 분야에서 궤적 최적화 기법(trajectory optimization techniques)는 역학적 제약조건 하에서 캐릭터 동작을 자동적으로 생성하는데 효과적으로 사용되어 왔다. 이 기법은 캐릭터의 미래 상태를 예측함으로써 단지 현재 상태만을 고려하는 다른 제어 기법에 비해 환경 변화나 외력에 대해 상당히 강인한 성능을 보여주어 왔다[1, 2. 2]. 하지만 전신(full-body) 캐릭터 동작에 대한 동역학 모델은 일반적으로 고차원의 비선형 시스템으로 표현되기 때문에 그러한 동역학에 기반한 궤적 최적화는 일반적으로 상당한 계산 비용을 요구한다. 더욱이, 캐릭터와 환경 사이의 접촉을 강체들(rigid bodies) 간의 충돌로 정형화 하는 경우, 미분 불가능한 역학적 제약조건이 초래되기 때문에 미분 정보에 기반하여 효율적인 궤적 최적화를 도입하기가 어렵다.
이 문제를 다루기 위해 여러 연구자들이 캐릭터와 환경 사이의 충돌을 부드럽게 완화시키는 접촉 동역학 모델을 도입하여 궤적 최적화 문제를 미분 가능하게 정형화 하였다[1, 4]. 하지만 이러한 기존 방법에서는 역학적 제약 조건에 대한 분석적 미분이 어렵거나 불가능하여 수치적 미분에 의존하여 궤적 최적화를 수행하였다. 일반적으로 수치적 미분은 분석적 미분에 비해 부정확한 미분 정보를 제공하기 때문에 궤적 최적화의 안정성에 영향을 미칠 수 있다.
본 논문에서는 이러한 문제를 다루기 위해, 접촉 완화(contact smoothing)[4]와 접촉 공간에서의 역질량행렬(inverse mass matrix)의 대각화[2]를 결합한 근사 기법에 기반 하여 분석적으로 미분 가능한 접촉 동역학 모델을 제안한다. 또한 그 접촉 동역학으로부터 유도된 닫힌 형식의 도함수를 사용하여 예제 데이터 없이 실행 시간에 주어지는 목표 위치와 목표 몸통 방향에 대한 사용자의 입력만으로도 이족 캐릭터의 동작을 빠르고 안정적으로 생성할 수 있는 온라인 궤적 최적화 기법을 제안한다. 이를 위해 현재로부터 가까운 미래까지의 시간 윈도우에 대한 캐릭터 동작에 사용자 입력을 효과적으로 반영시키기 위한 비용 함수(cost function)를 정형화 하고 시간의 흐름에 따라 그 윈도우를 이동시키며 비용함수를 반복적으로 최소화하는 전신(full-body) 모델 예측 제어(model predictive control (MPC)) 기법을 도입한다[2, 3].
본 논문의 공헌은 크게 두 가지이다. 첫째, 기술적인 측면에 있어서 적절한 근사화를 통해 접촉을 포함한 캐릭터 동작에 대한 역학적 제약조건을 닫힌 형식으로 유도하는 방법을 제안한다. 둘째, 시스템 구현 측면에서 이러한 미분 정보를 이용하여 예제 데이터 없이도 캐릭터 동작을 빠르면서도 안정적으로 생성할 수 있는 MPC 프레임워크를 제안한다.
본 논문의 구성은 다음과 같다. 2절에서는 관련 연구를 살펴보고, 3절에서는 시스템의 전체적인 구성에 대해 설명한다. 4절에서는 분석적으로 미분 가능한 시스템 동역학 모델을 유도한다. 5절에는 이러한 시스템 동역학 모델에 기반하여 이족 캐릭터의 동작을 예제 데이터 없이 생성하기 위한 궤적 최적화 기법에 대해 다룬다. 6절에서는 실험 결과에 대해 언급하고 7절에서는 제안된 기술의 한계와 향후 연구에 대해서 논한다.
2. 관련 연구
궤적 최적화 기법은 시스템 동역학 모델을 고려하여 캐릭터의 미래 상태를 예측함으로써 캐릭터 동작을 효과적으로 제어하는데 널리 사용되어 왔다. 이에 대한 많은 초기 연구들은 그 계산 비용이 너무 커서 오프라인 최적화로 수행되었으나[5, 6], 최근 최적 제어 이론의 도입은 실시간에 예제 데이터 동작에 대한 강인한 추적을 가능하게 하였다[7, 8, 9]. 이러한 제어 기법에서는 전처리 과정을 통해 추적하고자 하는 예제 데이터에 대한 최적 제어 정책(optimal control policy)을 미리 생성하고 실행시간에 그 정책을 사용하는 방식을 취했다. 하지만 실행시간에 온라인 방식으로 예제 동작이 변경되거나 환경이 변하는 경우에는 미리 계산된 컨트롤러만으로는 이러한 변화에 효과적으로 대응하기 어려울 수도 있다.
이 문제를 다루기 위해 많은 연구자들이 최적 제어 정책을 실행시간에 반복적으로 갱신하는 모델 예측 제어(MPC) 기법을 제안해 왔다[1, 2, 3, 10, 11]. 이러한 MPC 기법은 예제 동작의 변경이나 환경의 변화를 효과적으로 다룰 수 있지만 반복적인 제어 정책 갱신을 수행하는데 상당한 계산 비용이 요구되어 일반적으로 실시간 성능을 얻기가 어렵다. 전신 동역학 모델 대신, 저차원 동역학 모델에 기반한 MPC 기법은 이러한 계산 비용을 낮추어 실시간 또는 실시간에 가까운 성능을 얻는데 효과적으로 사용되어 왔다[1, 10, 11]. 저차원 동역학 모델은 일반적으로 특정 종류의 동작에 특화되어 있기 때문에 다른 종류의 동작으로 일반화 시키기가 어렵다.
최근 캐릭터의 전신 동역학에 기반한 MPC 기법에 대한 연구가 활발하게 진행되어 왔다. 환경과의 접촉을 포함한 캐릭터의 전신 동역학은 일반적으로 미분이 불가능 하기 때문에 샘플링에 기반한 MPC 기법이 제안되어 왔다[12, 13]. 이러한 방식에서 강인한 제어 성능을 얻기 위해서는 일반적으로 상당히 많은 샘플들을 필요로 하기 때문에 실시간 성능을 얻기 어렵다. 이 문제를 다루기 위해 많은 연구자들이 캐릭터와 환경 사이에서 발생하는 접촉력(contact force)을 완화시킴으로써 미분 가능한 전신 동역학을 유도하여 미분 정보에 기반한 MPC 기법을 제안해왔다[2, 3]. 일반적으로 이러한 미분 정보에 기반한 최적화 기법은 샘플링 기법에 비해 빠른 성능을 제공하지만 전신 동역학에 대한 분석적 미분이 불가능하여 수치적 미분에 의존해왔다. 본 논문에서는 몇 가지 근사화를 통해 분석적 미분이 가능한 전신 동역학을 유도하고 그에 기반하여 미분 정보를 정확하게 계산할 수 있는 MPC 기법을 제안한다.
최근 몇 년간 심층 강화학습(deep reinforcement learning)을 통해 얻은 제어기(controller)를 기반으로 실시간 동작 제어를 수행하는 물리기반 캐릭터 애니메이션 기법이 제안되어 왔다. 이 기법은 예제 데이터 추적[14], 농구 드리블 동작 수행[15], 비디오 동작 모방[16]에 성공적으로 적용되었다. 하지만 일반적으로 이 기법에서는 제어기를 생성하기 위한 학습 과정에서 상당히 많은 시간이 소요되는 제약사항이 있다. 이와는 달리, 본 논문에서 제안하는 MPC 기법은 전처리 학습 단계를 필요로 하지 않는다.
3. 시스템 개요
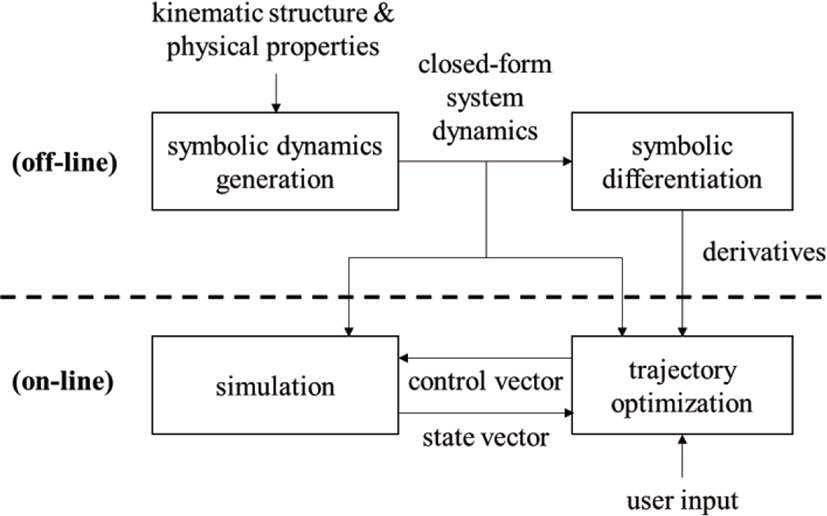
본 논문에서 제안하는 시스템은 크게 시스템 동역학과 관련된 수식을 생성하는 오프라인(off-line) 단계와 실행 시간에 그 수식에 기반하여 궤적 최적화와 시뮬레이션을 수행하는 온라인(on-line) 단계로 구분된다(Figure 1).
오프라인 단계의 기호 동역학 생성(symbolic dynamics generation) 컴포넌트에서는 캐릭터에 대한 기구학 구조(kinematic structure)와 질량과 관성 텐서(inertia tensor)와 같은 물리적 특성들(physical properties)이 주어지면 그에 해당하는 시스템 동역학의 기호 수식을 닫힌 형식으로 생성한다. 기호 미분(symbolic differentiation) 컴포넌트는 이것을 분석적으로 미분하여 시스템 동역학의 일차 도함수를 유도한다. 온라인 단계는 시뮬레이션(simulation)과 궤적 최적화(trajectory optimization) 컴포넌트로 구성되는데 전자는 캐릭터 동작을 제어하기 위한 관절 토크들(joint torques)로 구성된 제어 벡터(control vector)가 주어지면 이것을 시스템 동역학에 적용하여 캐릭터의 현재 상태를 나타내는 상태 벡터(state vector)를 갱신한다. 후자는 캐릭터의 현재 상태와 함께 단순히 목표 위치와 목표 몸통 방향에 대한 사용자 입력이 주어지면 이를 성취하기 위한 캐릭터의 동작 궤적을 오프라인 단계에서 유도된 닫힌 형식의 시스템 동역학과 도함수를 사용하여 빠르게 최적화하고 그 결과로 생성되는 최적 제어 정책(optimal control policy)을 통해 캐릭터 동작을 강인하게 제어하기 위한 제어 벡터를 계산한다. 여기서 실행 시간에 임의로 변할 수 있는 사용자 입력을 최적 제어 정책에 효과적으로 반영하기 위해 시간의 흐름에 따라 최적화 구간에 대한 시간 윈도우를 이동시키면서 반복적으로 궤적 최적화를 수행한다.
4. 시스템 동역학 모델
캐릭터의 시스템 동역학 모델은 매우 복잡하기 때문에 사람이 수작업으로 그에 대한 미분을 직접 구하는 것은 사실상 어렵다. 또한 시스템 동역학을 D*[17]와 같은 기존의 기호 미분(symbolic differentiation) 프레임워크를 통해 자동으로 미분하려면 이를 닫힌 형식으로 표현할 수 있어야 한다. 캐릭터와 환경 간의 접촉을 고려하는 경우 시스템 동역학 모델을 닫힌 형식으로 표현할 수 없고 또한 미분할 수도 없기 때문에 적절한 근사화가 필요하다. 이를 위해 본 절에서는 관절체 동역학에 기반하여 시스템 동역학 모델을 정형화하고(4.1절), 완화된 접촉 동역학에 기반한 대각 근사화[2]를 통해 이를 닫힌 형식으로 표현하는 방법을 소개한다(4.2절).
먼저, 자유도 n을 갖는 캐릭터의 자세를 q∈ℝn라고 하자. q의 각 원소는 그에 상응하는 관절의 좌표를 나타낸다. q를 사용하여, 캐릭터 동작에 대한 시스템 동역학[4]을 다음과 같이 기술할 수 있다.
여기서, q̇와 q̈ 는 각각 q의 시간에 대한 1차 및 2차 미분으로서 현재 시간 스텝에서의 관절 속도와 관절 가속도를 나타낸다. q̇+는 다음 시간 스텝에서의 관절 속도를 나타낸다. M0∈ℝn×n와 Ma=ρI∈ℝn×n은 각각 질량 행렬과 작은 계수 ρ를 갖는 회전자(armature) 관성 행렬이고, b∈ℝn는 중력, 코리올리스 힘(Coriolis force), 원심력과 외력을 나타내는 바이어스 힘(bias force)이다. 본 논문에서는 M0와 b에 대한 기호 수식을 라그랑지 역학(Lagrangian mechanics)을 통해 유도한다[18]. τ∈ℝn-6는 루트 관절을 제외한 나머지 관절에 작용하는 내부 관절 토크(internal joint torques)를 나타내고, B=kdI∈ℝn×n는 제동 계수(damping coefficient) kd를 갖는 제동 이득 행렬(damping gain matrix)을 나타낸다. J∈ℝ3nc×n는 nc개의 접촉점들에 대한 자코비안(Jacobian)이고 f∈ℝ3nc는 그 점들에서 작용하는 접촉력 (contact force )을 나타낸다.
상태 벡터와 제어 벡터를 각각 x=[qTq̇T]T와 u=τ라고 하면, 캐릭터의 시스템 동역학 모델, x+=g(x,u)는 다음과 같이 정형화 된다.
위 수식에서 h는 현재 시간 스텝에서 다음 스텝까지의 시간 간격(시뮬레이션 시간 스텝)이고, q̇+는 수식 (1)로부터 다음과 같이 유도된다.
여기서, Φ는 전체 질량 행렬(total mass matrix) M=M0+Ma+hB의 역행렬이고, f̂ =[(f̂1)T&(f̂nc)T]T∈ℝ3nc는 nc개의 접촉점에서의 충격량(impulses)이다.
수식 (3)에서 역행렬 Φ와 자코비안 J의 기호 수식을 직접 유도하는 것은 쉽지 않다. 전자의 경우, n×n 고차원 행렬인 전체 질량 행렬 M의 역행렬을 닫힌 형식으로 유도해야 하고, 후자의 경우, 캐릭터와 환경 사이의 접촉 상태에 따라 가능한 모든 자코비안 J의 기호 수식을 미리 모두 유도해 두는 것은 사실 상 불가능하다. 다음의 두 문단에서는 Φ와 J에 대한 기호 수식을 효과적으로 유도방법을 제안한다.
역행렬 Φ의 기호 수식 유도: M에 대한 기호 수식이 주어졌을 때, M에 대한 특성을 이용하여 그에 대한 역행렬 Φ의 기호 수식을 효과적으로 구하는 알고리즘을 다음과 같이 제안한다(Algorithm 1).
Function: derive_M_inverse(M)
Input: M (symbolic mass matrix)
Output: Φ (symbolic inverse of M)
(L, D) = LTDL_decomposition(M)
z = make a vector with new n symbolic variables
Solve z=LTDL s for s with a linear system solver.
for i=1 to n
for j=i to n
Φi,j = get_coefficient(si,zj)
for i=1 to n -1
for j=i+1 to n
Φi,j = get_ reference(Φi,j)
return Φ
여기서, LTDL_decomposition(M)는 질량 행렬 M의 대칭 양정부호(symmetric positive definite) 성질을 이용하여 M=LT DL을 만족시키는 하삼각(lower triangular) 행렬 L∈ℝn×n과 대각행렬 D∈ℝn×n을 기호 수식으로 구하는 함수이다[19]. 일단, M으로부터 L과 D를 구하면, 다음을 만족시키는 기호 수식 s∈ℝn를 구한다.
위 식에서 z∈ℝn는 Φ을 유도하기 위한 보조 벡터로서, 먼저 z=LTDL s 관계를 이용하여 하삼각 행렬에 특화된 선형 시스템 해결기(linear system solver)[19]를 가지고 s의 기호 수식을 유도하면, Φ의 상삼각(lower triangular) 원소들과 대각 원소들 Φi,j(i=1,…,n and j=i,…,n) 을 다음과 같이 구할 수 있다.
여기서, get_coefficient(si, zj)는 기호 수식 si에서 zi의 계수를 추출하는 함수이다. 한편, Φ이 대칭행렬인 속성을 이용하여 Φ의 하삼각 원소들 Φi,j(i=1,…,n-1 and j=i+1,…,n)은 다음과 같이 설정한다.
여기서, get_reference(Φi,j)는 Φi,j의 실제 수식이 아닌 참조(reference)만을 리턴하는 함수로서 Φj,i가 Φi,j의 별칭처럼 사용될 수 있게 한다. 이렇게 함으로써 일반적으로 상당히 복잡한 역행렬의 원소에 대한 중복 연산을 피하게 한다.
자코비안 J의 기호 수식 유도: 캐릭터와 환경 사이에 무한히 많은 접촉 상태가 가능하기 때문에 이에 대한 자코비안 J도 무한히 많은 구성을 가질 수 있다. 이 문제를 다루기 위해 본 논문에서는 캐릭터의 각 링크 상에 존재하는 임의의 접촉점에 대한 자코비안의 수식을 캐릭터 자세 q와 그 접촉점의 지역 좌표에 대한 함수로 표현하고 오프라인 수식 유도 과정을 통해 그에 대한 기호 함수만을 미리 유도한다. 온라인 단계에서는 이렇게 유도된 기호 수식들을 조합하여 캐릭터와 환경 간의 접촉 상태에 따라 접촉점 nc개에 대한 자코비안 J 을 구한다.
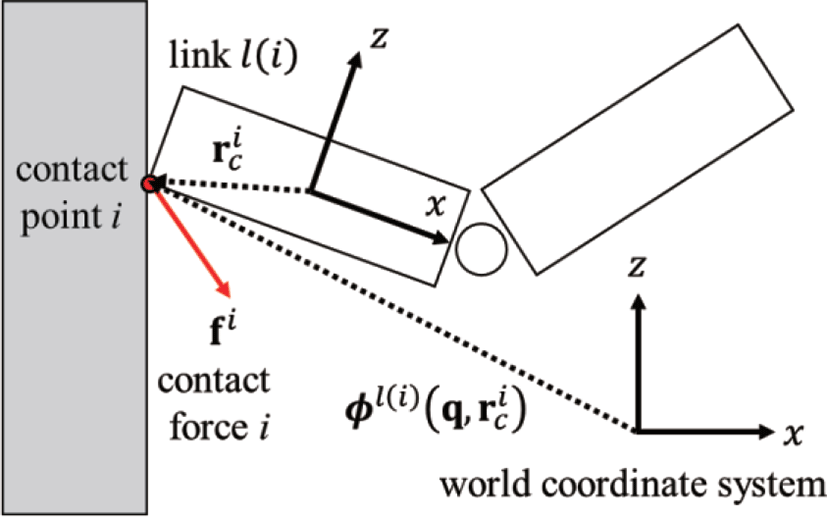
i∈{1,…,nc}번째 접촉점(contact point)의 지역 좌표 와 그 접촉점을 포함하는 링크의 인덱스 l(i)∈{1,…,nl}가 주어졌을 때, 그 점촉점의 전역 좌표를 라고 하면(Figure 2), nc개의 접촉점들에 대한 자코비안 J는 다음과 같다.
위와 같이 자코비안을 정형화 하는 경우, 오프라인 과정에서 유도해야할 기호 수식은 nl개의 링크로 구성된 캐릭터의 각 링크 j∈{1,…,nl} 대한 자코비안 뿐이므로(총 nl개) 다양한 형태의 접촉을 효과적으로 다룰 수 있다.
수식 (3)에서 충격량 f̂를 제외한 모든 항들은 분석적으로 미분 가능한 닫힌 형식의 수식들로 표현될 수 있다. 강체 충돌을 다루는 경우 f̂는 일반적으로 Coulomb의 마찰 법칙과 비침투(non-penetration) 제약조건에 따라 다음과 같은 Linear Complementarity Problem (LCP)을 풀어야 구할 수 있다.
위 식에서 는 각각 i 번째 충격량 f̂i∈ℝ3의 x,y,z 원소를 나타내고, μ≥0는 마찰 계수이며, v+∈ℝ3nc는 nc개의 접촉점에서 다음 시간 스텝에 대한 접촉 속도로서 다음과 같이 정형화 된다.
여기서 v∈ℝ3nc는 접촉 충격량이 적용되기 이전의 접촉 속도(contact velocity)이고 A∈ℝ3nc×3nc는 접촉 공간에서의 역질량 행렬(inverse mass matrix)이다. 일반적으로 LCP에 대한 해를 닫힌 형식으로 표현할 수 없고 이를 수치적 안정성을 갖고 정확하게 푸는 것은 어려운 문제로 알려져 있다[20]. 또한 강체 충돌에 의해 야기되는 관절체 동작의 급작스러운 변화는 미분 정보에 기반한 궤적 최적화 기법의 도입을 어렵게 만든다.
이 문제를 다루기 위해 본 논문에서는 완화된 접촉 동역학에 대한 근사화를 통해 f̂를 분석적으로 미분 가능한 수식으로 표현하는 방법을 제안한다. 먼저, LCP를 다음과 같은 convex optimization 문제로 변환하여 충격량을 완화시킨다[4].
여기서 R=γI∈ℝ3nc×3nc은 정규화 계수 γ≥0를 통해 접촉 충격량의 완화 정도를 조절하는 정규화 행렬(regularization matrix)이고 v*는 다음 시간 스텝에서의 목표 접촉 속도이다.
수식 (6)의 부등식 제약 조건으로 인해 f̂를 여전히 닫힌 형식의 해로 구할 수 없기 때문에 본 논문에서는 Tassa와 그의 동료들이 제안한 근사 기법을 적용한다[2]. 먼저, 부등식 제약조건이 없는 경우에 대한 해를 f̃라고 하면, f̃를 다음과 같은 닫힌 형식으로 구할 수 있다.
위 식에서 캐릭터와 환경 사이의 접촉 상태에 따라 A+R의 차원과 구성은 매우 다양하기 때문에 그 모든 경우에 대한 역행렬을 닫힌 형식으로 미리 유도해 놓는 것은 실질적으로 어렵다. A+R의 대각 성분만을 이용하여 역행렬을 구하는 대각 근사화 기법 [2]을 적용하면 다음과 같은 수식을 얻을 수 있다.
여기서, 는 i번째 접촉점 에서의 충격량, 접촉 속도, 목표 접촉 속도의 원소 j∈{x,y,z} 를 나타내고, 과 은 각각 에 상응하는 A와 R의 대각 성분으로서 다음과 같다.
위에서 연산자 (∙)i,j은 행렬의 (i,j) 원소를 의미한다. 수식 (8, 9)에서 유도된 링크 l(i)에 j∈{x,y,z} 축 방향을 따라 작용하는 충격량 를 살펴보면 다른 링크에서 작용하는 충격량의 영향을 고려하지 않기 때문에 캐릭터와 환경 사이의 접촉을 다루기 위해 실제로 닫힌 형식으로 미리 유도해야 하는 원소 별 충격량 수식의 개수는 3nl개에 불과하다. 일단 에 대한 수식이 위와 같이 유도되면, 완화된 부등식 제약 조건을 적용시킨 접촉 충격량 을 아래와 같이 닫힌 형식으로 정형화한다[2].
여기서, η는 대각 근사화를 통해 계산된 수직 항력 의 크기를 조절하기 위한 상수이고, ε>0은 마찰력의 크기 ζ가 정확히 0이 되는 것을 방지하기 위한 작은 상수이다(모든 실험에서 ε=10-10로 설정함). smax(x;β)와 smin(x,y;β)은 각각 max(x,0)과 min(x,y) 함수를 미분 가능하도록 완화시킨 함수로서 아래와 같이 정형화된다[2].
여기서 β는 smax(x;β)와 smin(x,y;β)가 각각 x=0와 x=y에서 얼마나 완화되는지를 조절하는 상수이다.
위와 같이 대각 근사화 및 완화된 부등식 제약조건을 적용하면 캐릭터와 환경 사이의 접촉점에서 침투나 발 미끄러짐이 발생할 수도 있기 때문에, 이를 보정하기 위해 다음 시간 스텝에서의 목표 속도 v*는 다음과 같이 설정한다.
위에서 첫 번째 두 식은 접촉 후에 지면에 대한 접속 속도가 0이 되도록 하여 미끄러짐을 방지하는 역할을 하고, 세 번째 식은 접촉 후에 접촉점의 높이가 지면 높이 zground가 되도록 하여 지면으로 침투하는 것을 방지하는 역할을 한다.
본 절에서 제안한 근사화 기법은 Tassa와 그의 동료들이 제안한 기존 방법[2]과 두 가지 면에서 중요한 차이점을 갖는다. 첫째, 본 논문에서는 수치적으로 좀더 안정적인 관절체 동역학(수식 (1))을 적용한다. 둘째, 기존 방법에서는 시스템 동역학에 대한 수치적 미분에 기반하여 궤적 최적화를 수행한 반면, 본 논문에서는 시스템 동역학에 대한 닫힌 형식의 수식을 기호 수식으로 완전하게 구현하고 그 수식에 대한 닫힌 형식의 도함수를 유도함으로써 궤적 최적화 시에 좀더 안정된 성능을 얻는다.
5. 궤적 최적화
이 절에서는 캐릭터의 루트 관절(root joint)이 캐릭터 몸통의 중심에 위치해 있다는 가정 하에 캐릭터의 현재 상태 x와 함께 온라인 사용자 입력으로부터 단순히 지면 상에서의 루트 관절의 목표 위치 및 z 축에 대한 루트 관절의 목표 회전각 만이 주어졌을 때, 예제 데이터 없이 그 입력에 따라 캐릭터 동작을 생성하기 위한 최적 제어 문제를 정형화 하고(5.1절) 그 문제를 풀어서 최적 제어 정책(optimal control policy)을 생성하는 방법에 대해 설명한다(5.2절).
캐릭터의 현재 상태 x가 주어졌을 때, 궤적 궤적화 문제는 x로부터 시작하여 N개의 프레임으로 구성된 시간 윈도우에 대한 최적 제어 문제로서 다음과 같이 정형화될 수 있다.
여기서, c(xi,ui)와 cf(xN)은 각각 시간 스텝 i=1,…,N−1와 마지막 시간 스텝에 대한 비용 함수(cost function)이다. 첫 번째 제약조건 x1= x은 최적화 되는 궤적이 캐릭터의 현재 상태로부터 시작되어야 한다는 것을 나타내고, 두 번째 제약조건 xi+1=g(xi,ui)은 시간 흐름에 따른 캐릭터의 상태 변화가 시스템 동역학 모델을 따라야 한다는 것을 나타낸다. 비용 함수 c(xi,ui)는 다음과 같이 정형화 된다.
첫 번째 비용 항 cbal(xi)은 프레임 i 에서 캐릭터의 균형 유지를 위해 지면에 사영(projection)시킨 질량 중심의 위치 가 왼쪽 발 위치 와 오른쪽 발 위치 의 중점에 오도록 하기 위한 항과 x축과 y축에 대한 루트 관절의 회전각 와 를 각각 0에 가깝게 유지하여 캐릭터의 몸통이 어느 한 쪽으로 기울지 않도록 하기 위한 항으로 다음과 같이 구성된다.
여기서 wcm와 wtor는 가중치 상수이다.
두 번째 비용 항 ctgt(xi)은 캐릭터가 사용자로부터 주어진 지면 위에서의 루트의 목표 위치 와 목표 방향 을 만족시키도록 하기 위한 항으로서 다음과 같이 정형화 된다.
, 는 프레임 i에서 지면 상의 루트 관절의 위치이고 는 z축에 대한 루트 관절의 회전각이며 , , 는 이들에 대한 목표값이다. , , 는 가중치 상수이다. sabs(x;α)는 x의 절대값 |x|을 부드럽게 완화시킨 함수로서 다음과 같이 정의 된다[2].
여기서 α는 sabs(·) 함수를 x=0 근처에서 완화시키는 정도를 나타낸다(모든 실험에서 α=0.1로 설정함). 위 함수는 프레임 i에서 루트 관절의 위치 가 목표 위치 로부터 많이 멀어져도 그에 대한 비용을 거의 선형으로 증가시켜서 제곱 형식의 비용 항을 사용하는 것에 비해 캐릭터가 목표 위치로 무리하게 이동하려는 것을 방지한다.
세 번째 항 crest(xi)은 캐릭터의 기본 상태(rest state)를 가능하면 유지하기 위한 항으로 다음과 같이 정형화 된다.
여기서, wjpos와 wjvel, wfrot는 가중치 상수이고, (zlf)i와 (zrf)i은 각각 프레임 i에서 왼발과 오른발의 지역 좌표계의 z축이고 e̅z은 이에 대한 목표값으로서 e̅z=[0 0 1]T로 설정하여 각 발이 지면과 평평한 상태를 유지하도록 한다.
마지막 항 cctrl(ui)은 에너지 소모 관점에서 효율적인 동작을 생성하기 위한 항으로서 다음과 같이 정의 된다.
여기서 wctrl은 가중치 상수이다.
본 논문에서는 위와 같이 정형화된 궤적 최적화 문제를 Differential Dynamic Programing (DDP) 해결기[21]의 하나인 iLQG(iterative Linear Quadratic Gaussian) 해결기를 통해 푼다[2]. iLQG는 시스템 동역학에 대한 1차 미분과 비용함수에 대한 1차 및 2차 미분 정보를 사용하며, 본 논문에서는 이들에 대한 모든 정보를 앞에서 정형화한 닫힌 형식의 수식들로부터 유도된 도함수들을 사용하여 빠르게 계산한다.
제안된 궤적 최적화 기법은 주기적으로 iLQG 해결기를 통해 5.1절에서 정형화된 최적 제어 문제를 푼다. 여기서 생성되는 결과물은 최적 제어 정책으로서 최적 상태 궤적 {x*1,…,x*N}, 최적 제어 궤적 {u*1,…,u*N−1}, 그리고 최적 피드백 이득 행렬 (feedback gain matrix) 시퀀스 {K*1,…,K*N−1}로 구성된다. 이러한 최적 제어 정책이 주어졌을 때, ti를 i번째 프레임 시간이라고 하고, 현재 캐릭터 상태 x에 대한 시뮬레이션 시간을 t∈[tk,tk+1)라고 하면 캐릭터에 적용하는 최적 피드백 제어 벡터는 다음과 같다.
여기서 두 번째 항은 캐릭터의 현재 상태 x가 그에 상응하는 최적 상태 x*k로부터 벗어 났을 때 그 차이를 보상해주는 역할을 한다.
6. 실험 결과
이 절에서는 구현 방법에 대한 상세 내역을 제공하고 (6.1절) 분석적으로 미분 가능한 시스템 동역학 모델에 기반하여 예제 데이터 없이 캐릭터 동작을 온라인 사용자 입력에 따라 생성하는 실험에 대한 결과에 대해 논한다 (6.2절).
오프라인 과정에서는 비용함수에 대한 1차 및 2차 도함수 뿐만 아니라 제안된 시스템 동역학 모델을 닫힌 형식으로 유도하고 그에 대한 도함수를 분석적으로 유도하기 위해 기호 미분을 지원하는 D* 프레임워크[18]를 사용하였다. 온라인 과정에서는 D* 프레임워크의 기호 수식에 대한 C 코드 변환 기능을 사용하여 시뮬레이션 및 궤적 최적화 프레임워크를 C/C++ 코드로 구현하였다. 실험에서는 Intel(R) Core™ i7-5930K CPU (6 cores)와 24GB RAM으로 구성된 컴퓨터를 사용하였으며 궤적 최적화 연산 시에 미분 정보 계산을 병렬로 처리하도록 하여 효율적으로 수행되도록 하였다.
실험에 사용된 캐릭터는 몸통(torso)과 두 다리로 구성된 단순화된 이족 모델(자유도 16, 총 질량 50kg)로 각 다리의 고관절(hip joint)과 발목관절은 2 자유도의 universal joint로 모델링하고 무릎관절은 1 자유도의 hinge joint로 모델링하였다. 궤적 최적화에서는 접촉 동역학을 많이 완화시켜서 좀더 먼 미래를 예측하도록 h=0.008 (125 fps), η=0.4, β=0.1로 설정한 반면 온라인 시뮬레이션에서는 캐릭터와 환경 사이의 접촉 시 침투(penetration)나 미끄러짐이 없는 좀더 안정적인 시뮬레이션을 위해 h=0.002 (500 fps), η=0.6, β=0.001로 설정하였다. 궤적 최적화에서 윈도우의 길이(N)는 35 프레임(0.28초)으로 설정하였다. 비용함수에 사용된 가중치 값은 아래 Table 1과 같다.
| wcm | 2×10−1 | wtor | 1×10−1 |
| , | 1×10−1 | 2×10−1 | |
| wjpos | 1×10−3 | wjvel | 1×10−5 |
| wfrot | 2×10−2 | wctrl | 8×10−9 |
수치적 미분과 분석적 미분 사이의 제어 안정성을 비교하기 위해, 사용자의 온라인 입력으로부터 지면 상에서의 캐릭터의 목표 위치 및 z 축에 대한 회전각으로 나타내는 목표 방향 이 주어졌을 때 수치적 미분에 기반한 궤적 최적화와 분석적 미분에 기반한 궤적 최적화를 통해 사용자 입력에 맞는 동작을 생성하는 실험을 수행하였다. 캐릭터 모델의 단순함과 시스템 동역학에 대한 도함수 수식의 복잡성으로 인해 분석적 미분의 속도가 수치적 미분의 속도와 큰 차이를 보여주지는 않았다. 실행 속도는 두 경우 모두 초당 프레임 수는 사용자 입력에 따라 300 ~ 400 fps 정도로 실시간(초당 500 프레임)보다 약간 느렸다. 제어 안정성에 있어서는 수치적 미분을 사용하는 경우 수치적 미분의 부정확성 때문에 캐릭터가 갑자기 급작스러운 동작을 보여주거나 균형을 잃는 경우가 종종 발생하였다. 반면에 분석적 미분을 사용하는 때는 궤적 최적화가 안정적으로 수렴하여 동작이 예상치 못하게 변하거나 캐릭터가 균형을 잃는 경우가 관찰되지 않았다.
7. 결론
본 논문에서는 접촉 동역학 모델에 대한 적절한 근사화를 통해 캐릭터 동작에 대한 시스템 동역학 모델을 분석적으로 미분하여 닫힌 형식의 도함수를 유도하는 새로운 방법을 제안하였다. 이를 위해, 자코비안과 전체 질량 행렬의 역행렬의 효과적인 유도 방법을 제안하였고, 접촉 완화[4]와 접촉 공간에서의 역질량행렬의 대각화[2]를 결합한 근사 기법을 활용하였다. 또한 이렇게 유도된 시스템 동역학 모델과 도함수를 활용하여 사용자의 온라인 입력에 따라 예제 데이터 없이 이족 캐릭터의 동작을 빠르고 안정적으로 생성하는 MPC 프레임워크를 제안하였다.
본 논문의 기술적인 측면에 있어서의 공헌은 적절한 근사화를 통해 접촉을 포함한 캐릭터 동작에 대한 역학적 제약조건을 닫힌 형식으로 유도하는 방법을 제안한 것이다. 시스템 구현 측면에서의 공헌은 이러한 미분 정보를 이용하여 예제 데이터 없이도 캐릭터 동작을 빠르고 안정적으로 생성할 수 있는 MPC 프레임워크를 제안한 것이다.
본 논문에서 제안한 분석적으로 미분 가능한 시스템 동역학은 닫힌 형식의 도함수를 제공하기 때문에 수치적 미분을 사용하는 경우에 비해 안정적인 궤적 최적화 성능을 제공하지만 몇 가지 해결 해야 할 한계점을 갖는다. 첫째, 충격량에 대한 닫힌 형식의 표현이 가능하도록 접촉 동역학을 적절하게 근사시켰지만 그로 인해서 시뮬레이션 시간 스텝 크기(h)가 충분히 작지 않은 경우 접촉면에서의 떨림이나 미끄러짐과 같은 부자연스러운 현상이 발생할 수 있다. 좀더 정확한 접촉 동역학 모델을 개발하여 이러한 현상을 경감시키는 것은 중요한 향후 연구 주제가 될 수 있을 것이다. 둘째, 자유도가 상당히 큰 모델에 대해 시스템 동역학 모델의 도함수를 유도하는 것은 지나치게 큰 수식을 초래할 수 있다. 이 경우, 상당히 큰 규모의 수식을 평가해야 하는 부담 때문에 분석적 도함수를 사용하는 것이 수치적 미분을 사용하는 것에 비해 오히려 궤적 최적화의 계산 효율을 많이 떨어뜨릴 수도 있다. 유도된 수식에 대한 분석을 통한 중복 수식 치환 및 인수 분해는 이 문제를 다루기 위한 하나의 접근방법이 될 수 있을 것이다. 끝으로, 본 논문에서 제안한 방법은 기존의 예제 데이터를 사용하는 방법에 비해 사용자 입력에 대한 캐릭터의 반응이 빠르고 다양하지만 동작이 부자연스러운 문제점이 있다. 이것은 계산학적 근육 모델[22, 23]이나 생체역학적인 관찰[24]에 기반한 비용 항을 통해 개선될 수 있을 것이다.