젖은 헤어에서 분사된 액체의 움직임을 표현하기 위한 FLIP 해법과 헤어의 결합 프레임워크

1. 서른

헤어 동역학은 사람의 헤어나동물의 털을 표현함에서 있어서 중요한시각적인 특징을 갖고 있기 때문에 컴퓨터 애니메이션 분야에서 꾸준히 연구되어 왔다 [1, 2, 3, 4, 5]. 유체 시뮬레이션에서는 물, 불, 연기 뿐만 아니라 날씨의 변화, 공기의 흐름 등 다양한 분야에서 활발하게 연구되어 왔다 [6, 7, 8, 9]. 해어와 유체의 상호작용에 관련된 연구의 진행은 아직 초기 단계이며, 최근에는 이런 분야를 연구하고자 몇 가지 기법들이 제안되었지만 대부분 젖은 헤어의 현상에 그 초점이 맞춰져 있다 [10,11, 12, 13, 14].

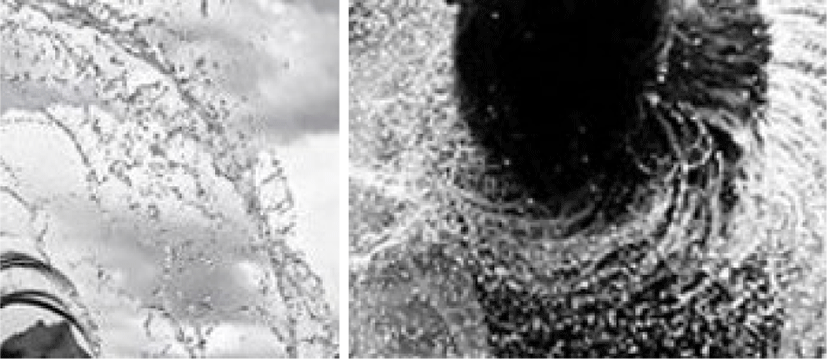
헤어와 액체 사이의 상호작용은 다양한 공간적 스케일에서 표현되는 물리현상이며, 최근에 Fei와 Maia는 이 문제를 풀어냄으로써 헤어와 액체 사이의 상호작용 결과를 개선시 켰다 [14]. 헤어가 액체 수중에 완전히 잠기면 헤어는 일종의 다공성 매 질(Porous material)처럼 해동하고 주변 흐름에 항력 (Drag force)을 전달하게 된다. 물속에서 벗어나게되면 머리카락은 그 표면에 일정 량의 액체를 보유하고, 그 다음 머리카락 가닥을 따라 흐르고 결국 떨어지게 된다. 한편, 젖은 머리카락은 머리카락 충돌 뿐만 아니라, 액 체 다리(Liquid bridge)의 표면 장력에 의해 젖은 머리카락들 사이에서 서로 상호작 용을 하게 된다. 또한, 뭉친 머리카락이나 동물의 털에 의해 액체는 곡선 형태를 띄면 분사되 게 된다 (see Figure 1). 그림에서 보듯이 동물의 털이나 사람이 머리카락이 젖게되면 뭉친 형태에서 액체가분사되기 때문에 곡선과 같은 움직임이 포착 된다. 하지만, 대부분의 해어-유체 상호작용 기술들이 헤어의 특징에만집중되어 있고유체의 디테일한움직임에 대해서는 만족할만한 결과를 만들어내지 못했다.

Figure 1: Curved spray motion of liquid by wet hair or fur.

Download Original Figure

이러한 한계점을 개선시키고자 본 논문에서는 젖은 헤어에 의해 곡선 형태로 움직 이는 유체의 디테일한 상호작용 효과를 시뮬레이션하는 새로운 프레임워크를 제 안한다. 우리는 액체 시뮬레이션을 표현하기 위해 FLIP 해법을 이용하였으며 [15], 해어 시뮬레이션은 DFTL(Dynamic follow-the-leader) 해법을 이용하였다 [16].

2. 관련 연구

컴퓨터 그래픽스 분야에서 해어 시뮬레이션의 연구는 Ward 등 [17]과 Hadap 등 [1]의 연구를 시작으로 많은 발전을 이루었다. 최근에는 머리카락의 길이가 늘어나지 않도록 제어하는 연구와 [18, 16], DER(Discrete elastic rod) [19] 프레 임워 크를 이용하여 위치 기반 동영학(PBD, Posi仕on-based dynamics) 과 통합하려는 연구도 진행되었다 [20, 21, 22]. Iben 등은 곱 슬 머리를 표현할 수 있는 기법을 제안했고 [5], Kaufman 등 은 [22] 비선형 적분 방법과 가우스 자이델 충돌 해법을 통합 하여 머리카락 사이에서 발생하는 충돌 처리 성능을 개선시 켰다. Gornowicz와 Borac은 충돌처리를 좀 더 안정적으로 처리하기 위한 하이브리드 입자-격자 알고리즘을 제안했다 [23]. 머리카락의 기본적인 움직임을 시뮬레이션하기 위해 본 논문에서는 DFTL 프레임워크를 이용하였고, 젖은 헤어와의 상호 작용 과정에서 분사되는 디테일한 유체의 움직을 모델링한다.

Rungjiratananon 등은 [10] 모발 내부에 유체를 전파시 키기 위해 다공성 유동(Porous flow) 접근법을 사용하여 SPH(Smoothed particle hydrodynamics) 기반 액체와 헤어 입자를 양방향으로 상호작용 할 수 있는 프레임워크를 제안했다. 그들은 헤어를 감싸고 있는 경 계 상자를 정규 격자화하여 다공 성 유동 모델을 이 산화하였고, Lenaerts 등이 [24] 제안한 SPH 기반 다공성 유동 기술을 적용시 켰다. Rungjiratananon의 방법에서는 인접한 머리카락 사이에 스프링과 같은 부착력을 사 용하여 젖은 머리카락 응집력을 계산하였다. Lin 등은 [12, 25] 유사한 다공성 모델을 제안했지만, SPH와DER 모델을 사용하 여 양방향으로 헤어와 유체가 상호작용 할 수 있는 새로운 프레임워크를 제시했다. 그들은 또한 물 속에서의 모발에 대한 부착력을 추가적으로 모델링했다. 위에서 언급했듯이 헤어와 액체의 상호작용을 표현하기 위한 다양한 방법들이 연구되어 왔지만 대부분 젖은 헤어의 특징 만들 고려하였다.

Lee 등은 헤어와 액체의 상호작용 기술을 제안했다 [26]. 이 들은 메쉬의 표면을 다면체(Tetrahedra) 메쉬로 근사하여 운동 량을 계산하였고, 이를 통해 헤어와 동물의 털을 사실적으로 표현하였다. 추가적으로, 액체와 헤어의 상호작용 기술도 제안하였지만 젖은 헤어나 털에서 표현되는 응집력과 접착력만을 모델링하였다. 이 뿐만 아니라, 헤어의 모델링과 스타일을 쉽게 제작할 수 있는 기법도 제안되었다 [27]. 기존의 해어 메쉬 기법을 [28] 개선하여 각각의 머리카락을 다양한 스타일의 헤어로 모델링할 수 있도록 Clustering과 Growing 기법을 제안 했다.

대부분의 연구들이 젖은 헤어의 특징에 만 집중한 연구들이며 본 연구에서는 액체-해어의 상호작용 결과를 개선시키기 위해, 곡선 형태로 액체의 분사를 표현할 수 있는 새로운 방법에 대해 소개 한다.

3. 제안하는 프레임워크

3.2 헤어 시물레이션

본 논문에서는 실시 간 탄성 체를 표 현할 때 자주 사용되는 PBD를 이용하여 헤어의 기본적인 움직임을 표현한다 [16]. PBD는 업데이트된 현재 위치로부터 다음 스텝의 새로운 속도를 예측 하여 안정적으로 다음 스텝의 위치를 결정한다. 헤어 입자의 위치 x와 속도 v가 주어지면, 이 알고리즘은 아래 절차에 따라 헤어 입자의 속도와 위치를 계산한다.

$$p\leftarrow x+\Delta tv+\Delta t^{2}f$$

(3)

$$p\leftarrow \mathrm{Solve}\mathrm{Constraints}(p)$$

(4)

$$v\leftarrow \frac{p-x}{\Delta t}$$

(5)

$$x\leftarrow p$$

(6)

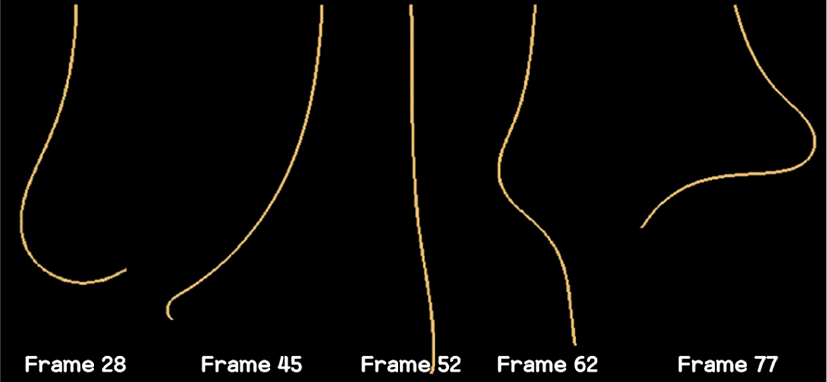
여기서 Δt는 타임 스텝이며, f는 외력이다. 모발의 초기 길이를 유지 시켜주기 위한 제약조건인 SolveConstraints(p) 함수는 PBD 기반의 DFTL 프로젝션 알고리즘을 이용하였다[16]. Figure 2는 DFTL기법을 기반으로 구현된 모발 하나를 시뮬레이션한 결과이며 큰 동작에 대해서도 안정적으로 모발의 움직임을 표현했다.DFTL 프로젝션은 각 모발이 갖고 있는 헤어 입자들 중 루트 입자를 제외한 2번째 입자에서 입자η번 째 순서대로 처리한다. 본 논문에서는 헤어 입자들 간의 거리가 초기 길이를 유지 하도록 헤어 입자들의 속도와 길이를 제어 한다. 결과적으로 하나의 헤어 입자위치가 결정되면, 이후의 입자들도 같은 방식으로 업데이트한다.

Figure 2: A strand simulation.

Download Original Figure

Figure 2는 하나의 머리카락을 시뮬레이션한 결과이다. 강한 외력에도 불구하고 질량-스프링(Mass-spring)기반의 접근법에 비해 모발의 길이가 늘어나지 않고 안정적으로 표현했다. 본 논문에서는 헤드뱅이나 젖은 털을 털었을 때 표현되는 액체의 움직임을 표현하고자 하기 때문에 강한 외력에도 안정적으로 시뮬레이션되는 기법이 필요했으며 질량-스프링 기반 접근법에 비해 DFTL기법 이 안정적으로 수행 되기에 이 기법을 헤어 시뮬레이션의 해법으로 사용하였다.

3.3 젖은 헤어와 유체의 상호작용에 의한 분사된 액체의 움직임

본 논문에서는 젖은 헤어에서 분사되는 액체를 표현하기 위해 입자-격자 기반의 FLIP 해법을 이용하며, 젖은 헤어에서 표현되는 응집력이나 강성 효과는 Kim 등이 제안한 방법을 이용하 였다 [13]. 이 기법은 실제 액체와의 상호작용은 다루지 않았 으며 이미 젖은 헤어라고 간주하고 젖은 헤어의 응집력 $F_{i\leftarrow j}^{*}$를 아래와 같이 모델링 했다 (Equation 7 참조).

$$F_{i\leftarrow j}^{*}=F_{i\leftarrow j}^{surface}+F_{i\leftarrow j}^{adhesion}$$

(7)

여기서 $F_{i\leftarrow j}^{adhesion}$와$F_{i\leftarrow j}^{surface}$는 각각 젖은 헤어의 자착력과 표면적을 최소화하기 위한 힘이다. Equation 8a에서 γ는 헤어 입자가 갖는 응집력의 크기이며, 머리카락의 루트부분에서 끝 단으로 갈 수록 잘 뭉치도록 함수의 커널 형태가 모델링했다. 젖은 헤어의 표면적 최소화는 아래와 같은 수식을 이용하여 계산한다 (Equation 8 참조).

$$F_{i\leftarrow j}^{surface}=-\gamma (l_i)m_i(n_i-n_j),$$

(8a)

$$\gamma (l)=\in O{\left(l\right)}^3$$

(8b)

$$O(l)=\mathrm{clamp}\left(\left(\frac{l-{\sigma }_{\min }}{{\sigma }_{\max }-{\sigma }_{\min }}\right),0,1\right)$$

(8c)

Equation 9a에서 δ와 ε은 자찰력계수와 헤어 입자 i와 j의 평균 유체 포화도이며, C(r)는 스플라인 함수 기반의 커널이다 Equation 9b,c에서 h는 커널의 반지름이며, R은 헤어 입자 i와 j의 반지름의 합인, R = r_a + r_b를 나타낸다. 이 커널 값은 헤어 입자간의 거리가충돌 거리인 R보다 클때부터 점진적으로 증가하여, $\frac{h}{2}$ 일 때 가장 큰 값을 가지게 된다.

$$F_{i\leftarrow j}^{adhesion}=-\delta \in C(|x_i-x_j|)\frac{x_i-x_j}{|x_i-x_j|},$$

(9a)

$$C(r)=\frac{32}{h^9}\{\begin{array}{cc}{(h-q)}^3{q}^3& r>R\wedge r\le h\\ 0& otherwise.\end{array},$$

(9b)

$$q(r)=\left(r+\frac{h}{2}-R\right)\frac{R}{h}$$

(9c)

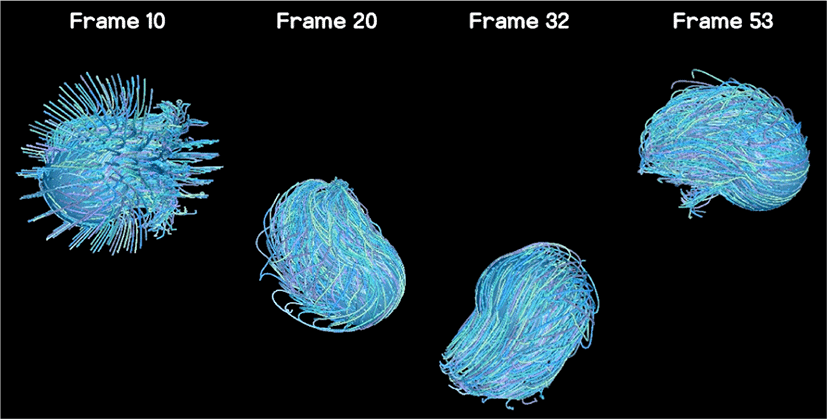
Figure 3은 회전하는 구에서 젖은 헤어의 움직임을 관찰한 결과이다. 마른 헤어에서는 흩날리는 움직임이 나타나는 반면, 이 결과는 구가 빠르게 회전함에도 불구하고 젖은 헤어의 특징인 응집력을 잘 표현했다.

Figure 3: Wet hair animations using Equation 7.

Download Original Figure

우리는 젖은 헤어에서분사되는 액체를표현하기위해헤어 입자들의 속도 v를 격자에 투영하여 비압축성속도장을 계산 한다 (Equation 10 참조).

$$u_v^{*}(x)=\frac{{\displaystyle \sum }_i{m}_i{v}_i{W}_i\eta (\Vert v\Vert )}{{\displaystyle \sum {}_i}{m}_i{W}_i},$$

(10a)

$$\eta (v)=\frac{1}{1+e^{-v+\phi }}$$

(10b)

우선 Equation 10a를 이용하여 헤어 입자들로부터 격자의 속도를 계산한다. 여기서 η (||v||)는 모발의 움직임에 따라 다르게 적용되는 커널이며，Equation 2에서 가중치가 추가된 형태이다 (Equation 10b 참조).

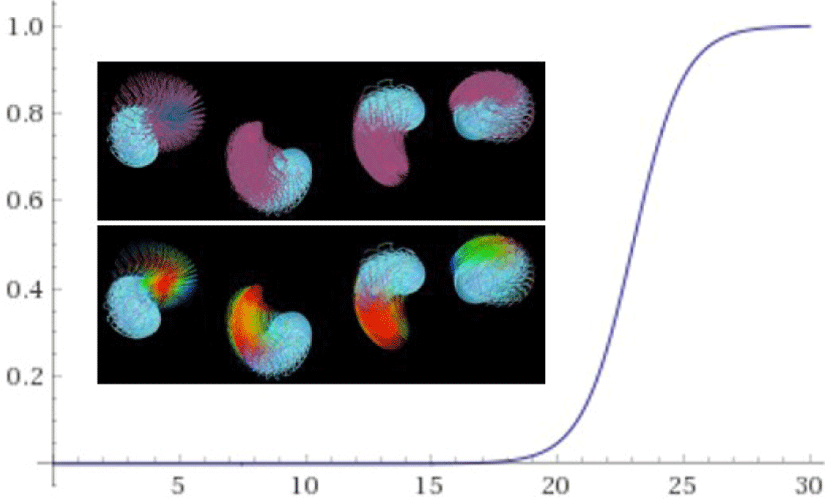
Figure4는 모발의 루트에서 팁까지 다르게 적용되는 커널의 크기를 시각화한 결과이며，여기서 φ를 조절하여 액체의 곡선 운동에 영향을 줄 수 있는 범위를 조절할 수 있다. 위 결과에서는 φ를 14로 설정하였으며，차트에서 보듯이 14 이후의 값에서는 급격하게 가중치 값이 증가되는 것을 볼 수 있다. X축인 헤어 입자의 인텍스는 루트에서 팁 인 모발의 끝으로 갈수록 증가하는 구조이며，결과적으로 찰랑거 리는 모발의 움직임이 강하게 나타나는 모발의 끝부분이 액체의 곡선 운동에 영향을 강하게 준다. Figure 4에서 위에 있는 그림은 가중치 값이 0보다큰 곳을 표현한 결과이며，아래 그림은 가중치가 증가되는 영역에서부터 크기에 따라 색을 표시한 결과이다. 이 그림에서 빨간색 일수록 강한 가중치 값을 의미하며，φ 값이 작을 수록 가중치가 중가되는 영역이 넓어지므로 결과적으로 모발의 곡선 운동에 더 강한 영향을 주게된다. 여기서 가중치가 증가되는 영역이 넓어진다는 의미는 모발의 끝이 아닌，모발의 루트에서부터 영향을 주도록 설정할 수 있다는 것을 의미하며， 이 영역은 사용자가 쉽게 제어 할 수 있다.

Figure 4: The shape of weighting function inside the kernel η (φ : 14, X-axis : index of hair particle, Y-axis : weight value).

Download Original Figure

$u_v^{*}(x)$는 격자상에서의 속도를 의미하며，v_i는 헤어 입자의 속도이고，W_i는 헤어 입자가 x의 위치에 영향을 미치는 가중치로써 Gaussian 함수 기반으로 가중치 값을 계산하며，Equation 2a에 의해 격자에서의 속도장이 계산된다. $u_v^{*}(x)$가 계산되면，본 논문에서는 이 속도장을 Naiver-Stokes 방정식에 외력인 f에 추가하여，프로젝션 과정을 거쳐 비 압축성이 적용된 속도장인 u (x)를 얻어 낸다 (Equation 11 참조).

$$u_t+\left(u\cdot \nabla \right)u+\nabla p/\rho =f,$$

(11a)

$$\nabla \cdot u=0$$

(11b)

본 논문에서는 비압축성을 나타내는 Equation 11b를 만족 시키기 위해 Chorin의 프로젝션 기법을 적용했고 [29], Equation 11a를 두 개의 수식으로 분해하여 계산했다 (Equation 12 참조).

$$\frac{u^{*}{u}^n}{\nabla t}=-\left(u^n\cdot \nabla \right)u^n+f,$$

(12a)

$$\frac{u^{n+1}-u^{\ast }}{\Delta t}=\frac{\nabla p}{\rho }$$

(12b)

여기서 uⁿ으로부터 uⁿ⁺¹을 얻기위해 먼저, Equation 12a에서 — (uⁿ · Λ) uⁿ와 f를 계산한 후, u*를 계산하고, Equation 12b에서는 u*로부터 비압축성을 만족하는 uⁿ⁺¹를 계산한다. 본 논문에서는 하이브리드 해법 인 FLIP을 사용하기 때문에 마지 막으로 Equation 2c를 이용하여 유체 입자를 속도를 계산한다. 여기서 $\left(u_i^n+u^{*}\left(p_i\right)-u\left(p_i\right)\right)$ 항을 통해 프로젝션 전/후의 속도 차이를 계산할 수 있고, 얼마큼의 속도를 적용해야만 비 압축성을 유지 할 수 있는지 알 수 있으며, 이를 통해 Divergence-free 한 유체의 움직임을 표현할 수 있다.

4. 구현

본 논문은 다음과 같은 환경에서 구현되었다 : 인텔 i7-770k 4.20GHz CPU 32GB RAM, NVIDIA GeForce GTX 1080 Ti 그래픽 카드. 헤어 시뮬레이션은 DFTL기법을 사용하였고 [16], FLIP기반 해법을 기반액 체(Underlying water) 시뮬레이션으로 사용하였다 [15]. 유체의 압력을 계산하는 수치적 행렬해법은 GPU 기반 선조건 적용 켤레 기울기법(Preconditioned conjugate gradient) 방법을 이용하였다 [30]. FLIP 격자의 경우 모든 운동량은 Staggered Marker-and-Cell 방법을 사용해 저 장했으며 [31], 표면 재복원을 위해 격자를 추가적으로 사용하였다.

5. 결과

본 논문에서는 제안하는 기법을 다양한 방면으로 분석하기 위해 3가지 시나리오로 비교해보았다.

먼제 제안하는 기법의 우수성을 입증하기 위해 간단한 테 스트 시나리오로, 구형 객체에 헤어 입자들을 추가하여 위/아 래로 움직 이는 장면을 제작했다. Figure 5에서 유체와 헤어를 표현하기 위해 타임 스텝을 0.006으로 설정하고, 약 22만개의 유체 입자와 15만개의 헤어 입자를 사용하였다.

Figure 5: Quality comparison between (a) our method and (b) previous method [14].

Download Original Figure

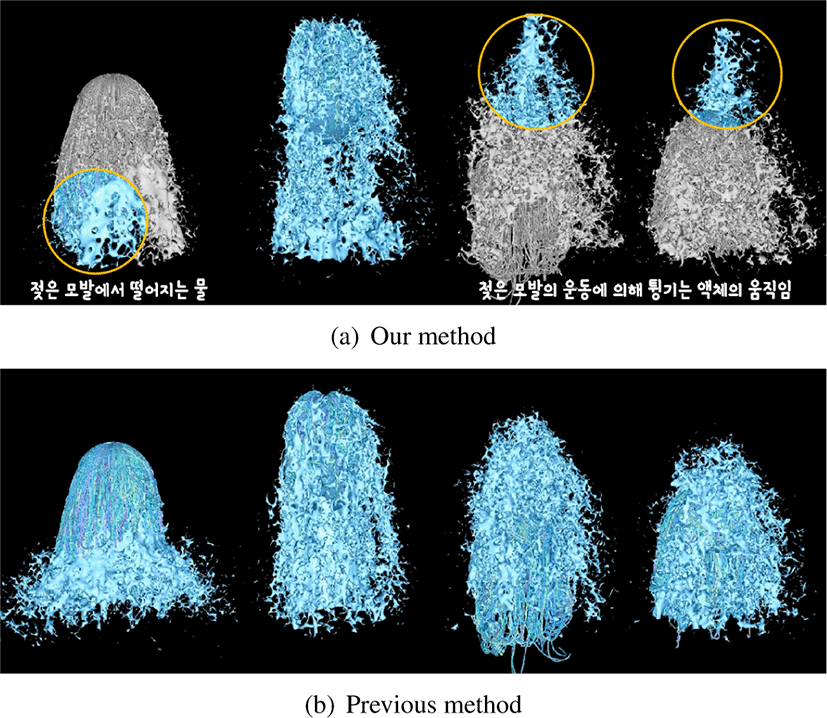
헤어와 유체의 상호작용 기법은 최근에 제안된 Fei와 Maia가 제안한 기법과 비교하였다 [14]. Fei의 기법은 젖은 헤어의 응집력과 유체의 움직임을 훌륭하게 표현하였지만, 그 초점이 젖은 헤어의 특징을 잡아내려 했기에 오히려 유체의 움직임은 디테일이 떨어지는 결과를 보였다. 우리는 젖은 헤어에서 분사되는 유체의 동적인 움직임을 관찰하게 위해 모발이 생성되 어 있는 구형 객체를 위/아래와 강하게 움직 였다. 젖은 모발이 뭉치게되면, 뭉친 형태를 유지하면서 물이 떨어지는 특징이 있는데 이전기법과 비교했을 때 제안하는 기법은 이 특징을 잘 표현했다 (Figure 5a 참조). 또한, 구형 객체가 위에서 아래로 방향을 바꾸는 순간 모발의 방향도 바뀌고 되고, 그로 인해 젖은 모발에서 분사되는 유체 또한 위로 튀어오르는 현 상이 발생하게되는데 이전 기법에서는 이러한 특징을 제대로 캡처하지 못했다. 그에 비해, 제안하는 기법은 이러한 특징을 잘표현하였고, Figure 5a에서 보듯이, 액체가위로 튀어오르는 결과를 쉽게 확인할 수 있다.

Figure 6은 Figure 5의 장면에 흡수 맵(Absorption map)을 추 가한 결과이다. 그림에서 모발의 색상은 빨간색일 수록 물을 흡수한 양이 큰것이며, 파란색일수록 마른 헤어로 변화하는 과정을 보여주는 결과이다. 헤어의 움직임에 따라 젖은 해어가 마른 헤어로 변화하는 것은 Fie의 기법을 사용하였으며 [14], 나머지는 제안한 방법을 이용하여 상호작용한 결과이다. 노란색으로 표시한 부분에서 보이듯이 물이 흡수가 남 아있는 젖은 모발의 경우 유체가 뭉친 모발의 형태에 맞게 분사되는 결과를 보이는 반면, 마른 모발 영역에서는 물이 분사 되지 않는 결과를 잘 보여준다.

Figure 6: Simulation results of hair with water absorption (inset image : colored by absorption).

Download Original Figure

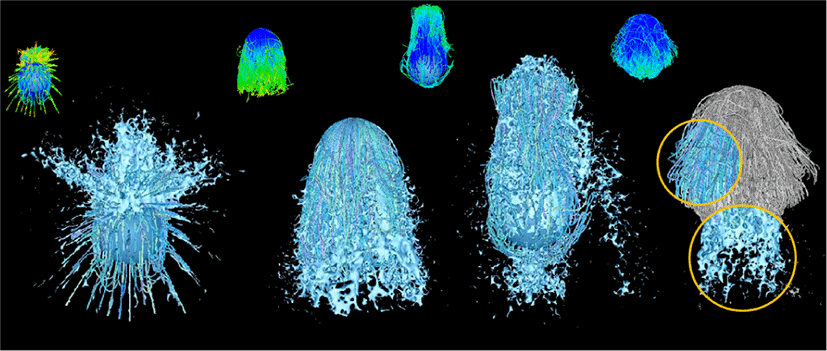
Figure 7은 구형 객체를 반구 형태로 회전시켜 그에 따른 젖은 헤어과 그로 인해 분사되는 유체의 결과를 관찰하기 위한 결과이다. 앞에서 보여준 결과에 비해 명확하게 곡선형태의 움직임이 잘 보이는 결과이다. Figure 7a는 제안한 방법을 이용한 결과이며 유체의 움직임이 젖은 머리카락의 움직임과 유사한 곡선 형태를 유지하지는 것을 볼 수 있다. 그에 비해, 이전 기법은 중력방향으로 떨어지는 물방울 움직임을 잘 표현하지만, 이 장면처럼 곡선 형태로 움직이는 결과에 대해서는 좋지 않은 결과를 만들어 냈다 (Figure 7b 참조).

Figure 7: Quality comparison between (a) our method and (b) previous method [14].

Download Original Figure

Table 1은 본 논문에서 실험 한 시뮬레이션 환경을 측정한 값이며, 이전 기법과 비교했을 때 결과품질에 대한차이가명확 하게 나타난다는 점에서 제안하는 기법의 우수성을 다시 한번 확인할 수 있다.

6. 결론 및 향후 연구

본 논문에서는 헤어와유체의 상호작용에서 표현되는 액체의 곡선 운동을 표현할 수 있는 효율적인 알고리즘을 소개했다. 젖은 헤어에서 표현되는 뭉친 형태를 고려하여 액체를 표현 하기 위해 헤어의 속도를 격자에 투영 시키고 프로젝션 과정을 거쳐 Divergence-free한 유체의 속도장을 계산했다. 이 과정에서 젖은 모발의 뭉친 형태가 강하게 나타나는 모발의 끝 부 분을 기반으로 액체의 곡선 운동에 영향을 줄 수 있는 범위를 조절하였다.

우리의 방법은 젖은 헤어에서 표현되는 액체의 곡선 운동을 잘 표현하지만 여전히 부족한 점을 가지고 있다. 젖은 헤어 나 동물의 털에서는 곡선 방향으로 액체 시트가 표현되지만, 제안하는 방법은 이정도 디테일한 특징까지는 잡아내 지 못한다 (Figure 8 참조). 향후연구로, 우리는 젖은 헤어에서 표현되는 디테일하고 다양한 특징을 표현하기 위해 젖은 모발의 궤적에 따라유체 시트가표현될 수 있는 기법에 대해 연구할 계획이다.

Figure 8: Generation of liquid sheets on wet hair and fur.

Download Original Figure