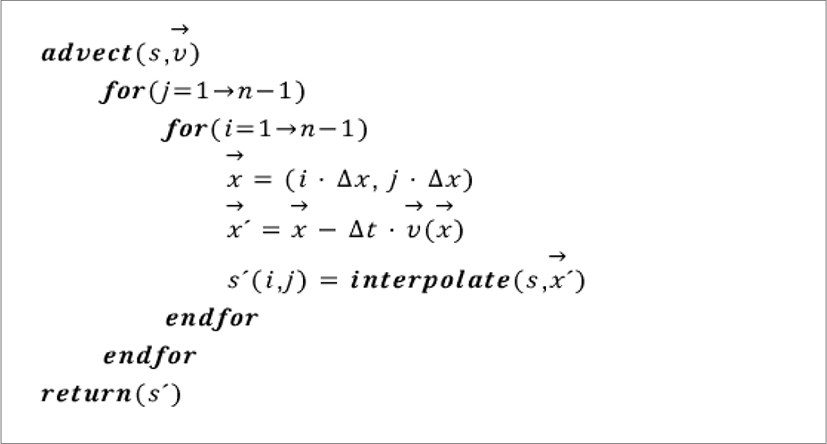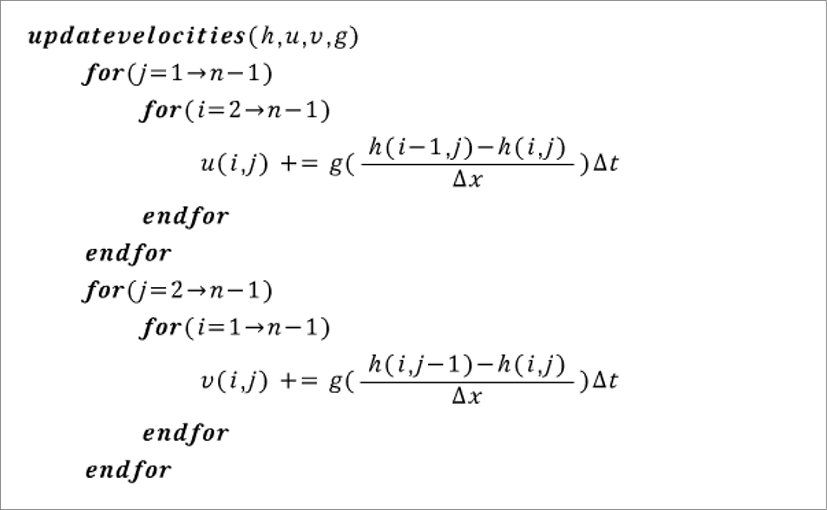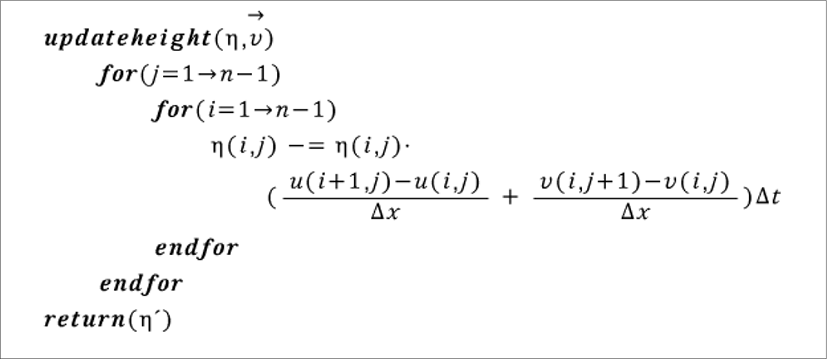1. 서른
지구상에서 관찰할 수 있는 자연 현상들의 사실적 표현은 컴퓨터 그래픽스 분야의 필수적인 목표이다. 그중에서도 물은 자연에서 가장 흔하게 관찰할 수 있는 물질 중 하나로서, 이를 사실적으로 표현하기 위한 기술은 매우 중요한 과제로 연구되어왔다. 현재는 전산유체역학의 이론을 이용한 시뮬레이션 기법으로 이와 같은 물의 움직임을 보다 사실적으로 재현하고 있다.
유체를 시뮬레이션하기 위해서는 유체의 움직임을 의미하는 지배방정식을 풀어야 한다. 이는 Navier-Stokes 방정식이라 불리는 비선형 편미분 방정식으로 표현된다. 유체 시뮬레이션은 실제의 물리량을 이산화하고 그 값을 컴퓨터의 반복 연산으로 풀어내는 방식으로 유체의 움직임을 재현한다. 물이 깊이에 비해 너비가 훨씬 크고 상하 유동이 적은 상태일 경우 3차원의 Navier-Stokes 방정식은 2차원으로 간략화할 수 있으며 이를 천수방정식(Shallow Water Equation; SWE)이라 한다.
이 논문에서는 천수방정식의 대류항을 푸는 과정에서 발생하는 수치적 손실을 줄이기 위해 Constrained Interpolation Profile(CIP)법을 도입할 것이며, 천수에서 특히 중요한 물리량인 높이값을 보존하기 위해 일반적인 CIP를 개선한 방법, CUSCIP(Conservative Unsplit Semi-lagrangian CIP)를 제안한다.
2. 관련 연구
Kass와 Miller[3]는 2차원 천수방정식으로 높이 필드를 구하여 수면을 표현하였다. 이후 Layton과 Panne[13]은 안정성을 보장하는 시뮬레이션 방법을 개발했다. Yuksel, House, Keyser[14]는 접근 방식을 바꾸어 높이값을 변화시키는 파동 자체를 하나의 입자(particle)로 보고 그 입자를 시뮬레이션하는 방법을 사용하였다. Jeschke와 Wojtan[15]은 입자를 파동묶음(wave paket)으로 확장하여 다양한 주파수의 수면파를 시뮬레이션 하는 방법을 개발하였다. Lee와 Han[16]은 2차원 상에 체적값을 갖는 입자들을 SPH[17]로 시뮬레이션하여 천수방정식을 푸는 방법을 제안하였다. 수면파를 이산 푸리에 변환으로 해석하여 움직임을 표현하는 방법들도 제안되었다[18,19]. 한편, 쇄파나 분무 현상을 표현 못하는 천수방정식의 한계를 극복하기 위해 다양한 논문들이 발표되었다. O'Brien과 Hodgins[20], Thürey와 동료들[21]은 이 문제를 입자 시스템(particle system)을 도입하여 해결하였다. 즉, 높이 필드에서 쇄파나 분무 현상이 일어날 곳을 찾아 그 위치에 입자를 생성하는 방식이다. Irving과 동료들[22]은 쇄파나 분무 같은 세밀한 현상이 물 표면에서만 일어난다는 사실에 착안하여 2차원 격자 기반의 높이 필드와 일반적인 3차원 유체 시뮬레이션을 결합하는 방법을 제안하였다.
한편, 유체 시뮬레이션 대류항을 계산하는 가장 대표적인 수치 해법은 세미-라그랑지안 기법(Semi-Lagrangian method)이다. 전산 유체역학 분야에서 Courant, Isaacson, Rees[1]에 의해 제안되었고 그래픽스 분야에서는 Stam[2]이 최초로 소개하였다. 대류항을 수치적으로 풀 때 필요한 보간 과정에서의 정확도를 높이기 위해 Yabe와 동료들[4,5,6,7]은 CIP법을 고안하였다. CIP법은 물리량을 보간할 때 미분값을 함께 고려하는 방법이다. 최초의 CIP는 안정성을 보장하지 못하는 문제를 가지고 있었다. Song과 Shin, Ko는 CIP의 안정성 문제를 해결하기 위해 미분값을 보정하는 Monotonic CIP(MCIP)법을 제안하였다[8]. 이 방법은 Courant-Friedrichs-Lewy(CFL)조건에 무관하게 안정적이다. 이후 Kim 등은 [8]에서 야기되는 차원 분할 과정을 생략하기 위해 Unsplit Semi-lagrangian CIP(USCIP)법을 제안하였다[9]. 이 방법은 MCIP보다 정확도가 향상 되었으며, 계산 비용을 대폭 절감하였다. 물리량을 보존하기 위해 개발된 CIP-Conservative Semi-Lagrangian(CIP-CSL)법[10,11]은 적분값을 함께 고려한다. 2009년 Yabe와 Ogata는 이를 천수방정식에 적용하는 방법을 소개하였다[12].
3. 천수방정식의 수치해법
천수방정식을 유도하기 위해서는 다음과 같은 조건들이 필요하다.
-
유체는 얕은(shallow) 상태이다. 이는 수평 방향의 크기가 수직 방향의 크기보다 월등히 크다는 것을 의미한다.
-
유체는 유동이 적은, 안정적인 상태이다. 유체는 특정한 방향으로 흐르고 있지 않으며, 기본적으로 작용하는 외력은 중력뿐이다. 따라서 압력은 더 이상 미지의 값이 아니며, 깊이에 따라 선형으로 비례한다.
-
유체는 높이값을 갖는 자유표면으로 표현된다(height field). 따라서 쇄파(breaking wave)나 분무(spray)현상은 표현할 수 없다.
이와 같은 조건으로부터 유체는 수직 방향으로의 속도 변화를 무시할 수 있으며, 연직 방향에 대하여 정역학적(hydrostatic)상태라는 가정이 가능하다. 따라서 유체의 압력은 중력의 영향만을 고려하여 유체의 깊이에 선형으로 비례한다. 여기서 주의할 점은 수직 방향의 속도가 반드시 0은 아니라는 점이다. 속도의 수직 성분은 유체가 존재하는 지면의 높이와 중력에 의해 발생하며, 수평 방향의 속도가 깊이 변화에 영향을 받지 않을 뿐이다. 이와 같은 가정들을 고려하여, 일반적인 유체의 지배방정식인 Navier-Stokes 방정식으로부터 천수방정식을 유도할 수 있다.
점성을 고려하지 않을 경우, Navier-Stokes 방정식은 다음과 같이 표현된다:
위 식에서 첫 번째 식은 유체의 속도에 대한 식이며, 두 번째 식은 비압축성에 대한 식이다. 는 유체의 속도 필드, t는 시간, ρ는 밀도, 는 외력, 그리고 p는 압력을 의미한다. 속도는 방향을 가지고 있으므로 3차원 벡터 (u,v,w)로 표현되며, 여기서 연직 방향의 성분 v에 대한 식만 살펴보면 다음과 같다:
g는 중력가속도이며 연직방향의 성분에만 영향을 미친다. 위의 가정에 의해, 성분 v의 대류항들을 무시할 수 있으며, 이에 따라 중력가속도 g에 의한 압력의 관계식으로 간략화 된다:
y=h(h는 물 표면 지점의 높이)인 지점에서 p=0이므로 이를 p에 대한 식으로 다시 쓰면, 아래와 같다:
수평 성분의 방정식에서 가정에 의해 이며, 식(4)에 의해 압력 구배에 대한 항은 높이의 구배로 치환할 수 있다:
이처럼 연직 방향의 속도 변화를 무시하고 수평 성분의 속도로 관계식을 새로 정립함으로써 속도에 대한 3차원 미분방정식을 2차원으로 간략화 하였다.
일반적으로 유체의 표면은 레벨셋 값(level set value)[23] ϕ가 0인 지점으로 생각할 수 있으며, 천수의 경우 y=h인 지점에 해당한다. 따라서 ϕ(x,y,z)=y−h(x,z)로 치환이 가능하며, 이 값은 대류 방정식을 만족한다:
여기서, 수직 성분 v는 비압축성 조건을 이용하여 구할 수 있다. 비압축성 조건에 따라 y에 따른 v의 변화율은 아래와 같다:
v를 구하기 위해 필요한 유체와 지표면 사이의 경계조건은 이며, 지표면 b(x,z)에서의 법선벡터는 에 비례하므로, 경계 조건에 적용하면,
로 정리된다. 이제 식(8)을 식(6)에 대입한 후 정리하면 천수의 높이값에 대한 편미분방정식이 아래와 같이 유도된다:
여기서, 지면으로부터 수면까지의 거리(h-b)를 η로 치환하고 수평 방향의 속도, 에 대한 식(5)과 함께 정리하면 최종적으로 천수방정식은 아래와 같다:
이 수식이 의미하는 바를 살펴보면, 각각의 물리량 η,는 수평 속도 에 따라 대류하고, 속도는 높이값 h의 구배에 의해 발생하며, η는 속도 필드의 발산(divergence)에 의해 변화하는 것을 알 수 있다. 이로써 풀어야 하는 공간 격자는 2차원으로 줄어들었다. 뿐만 아니라 압력을 미리 정해진 값으로 가정하고 있으므로 압력 분포를 알아내기 위한 선형 시스템을 풀 필요가 없는 것도 큰 이점이다.
천수방정식은 대류항(advection term)과 비대류항(non-advection term)으로 나뉘어지는데, 대류항은 Semi-lagrangian 기법으로 풀 수 있다.
식(10)의 좌변이 대류항인데 이를 다시 쓰면,
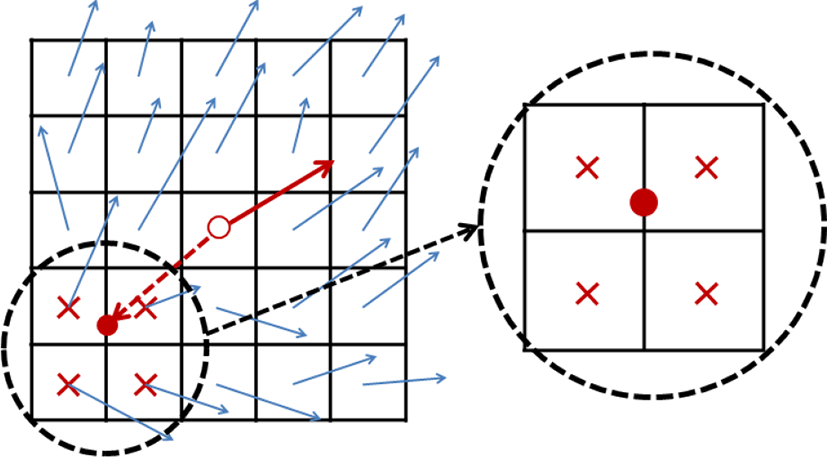
위 식은 속도와 물의 높이가 격자점 중심의 속도장을 따라 움직이는 것을 나타낸다. Semi-lagrangian 기법은 먼저, 속도장 위에 입자가 존재한다고 가정한다(Figure 1에서 격자 중앙에 빨간색 실선으로 표시된 원). 현재 격자의 중심에 입자들이 있고 속도장이 정의되어 있다면 그곳에 정의된 속도 벡터 값에 따라 그 입자들의 이전 타임 스텝에서의 위치를 역으로 추적하여 알아낼 수 있다(Figure 1에서 빨간 점선으로 표시된 벡터를 따라 이동한 지점의 원). 물론 역으로 계산된 입자의 위치는 격자의 중앙이 아닌 경우가 대부분이므로 인접한 네 개의 격자(X자 형태로 표시된 부분)를 기준으로 보간(interpolation)하는 과정이 필요하다. 이렇게 계산된 물리량을 현재의 값에 반영하여 대류항을 풀 수 있다. 대류 항을 푸는 알고리즘을 의사코드로 요약하면 다음과 같다.
식(10)의 우변인 비대류항은 유한차분법으로 풀 수 있다. 위에서 대류항을 푼 이후의 물리량을 각각 , η*라고 한다면, 최종적으로 구해지는 다음 타임스텝에서의 값 은
이며, 유한차분법으로 변환하면 격자 i,j에서의 값은
이 된다. 따라서, 속도와 높이에 대한 비대류항 식을 푸는 과정은 다음과 같이 요약된다.
위의 절차들을 종합하여, 천수방정식을 푸는 알고리즘은 다음과 같이 정리된다.
4. 천수방정식에서의 Constrained Interpolation Profile(CIP)법
Constrained Interpolation Profile(CIP)법으로 대류항을 푸는 방법을 설명하기 위해, 아래의 1차원의 대류 방정식을 보면,
수치적인 해법으로 이 문제를 풀 것이므로, 격자점 xi, xi+1과 이에 대응하는 물리량 ϕi, ϕi+1만을 알 수 있고, 그 사이 지점에 대응하는 물리량은 보간하여 구한다.
가장 간단한 보간법은 선형 보간법이다. 선형 보간식은 식(15)와 같은 형태의 1차식이며, 선형 보간된 물리량의 변화는 Figure 2와 같다.
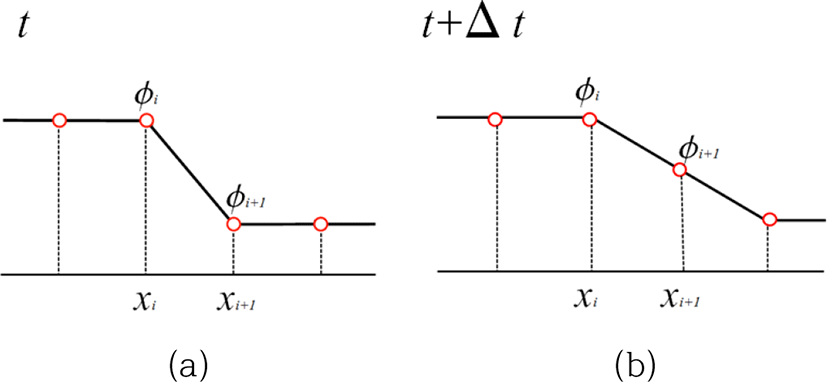
선형 보간법은 간단하고 안정적이지만 1차의 정확도만을 가지므로, Figure 2에서 보듯이 수치 소산이 빠르게 일어난다. CIP법은 Figure 3에서 보는 바와 같이, 값을 보간하는 과정에서 주어진 값뿐만 아니라 그 미분값까지 함께 감안하는 것이 기본 아이디어이다. 대류항의 미분식은 식(14)를 x로 미분하여,
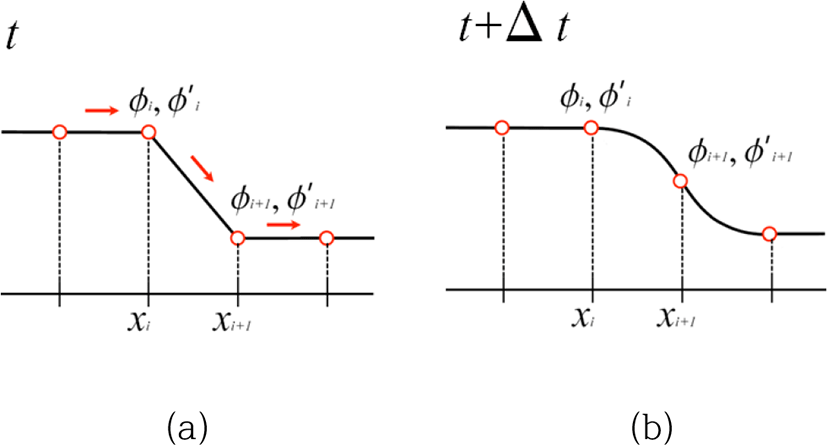
로 표현할 수 있다. 즉, 각 격자점에 정의된 값 ϕ와 그 미분값 ϕx를 모두 알아내면, 이를 기반으로 ϕ에 대한 3차 보간식을 세울 수 있다. 편의상 격자점 사이의 거리를 1로 정규화하였을 때, 보간식은 다음과 같다:
여기서, C0와 C1은 격자점 상의 ϕ와 ϕx로 이루어진 계수로,
이 된다. 천수방정식에 적용하기 위해서 이를 2차원으로 확장할 경우, CIP식은 두 개의 공간 변수 x,y 에 대한 3차 다항식으로 표현된다:
CIP를 처음 소개한 Yabe와 동료들은 자신의 논문에서 CIP의 2차원 및 3차원 다항식에 대한 계수를 밝힌 바 있다[7]. CIP는 3차의 정확도를 가지고 있으며 이로 인해 얻을 수 있는 시각적인 세밀함은 선형 보간법보다 월등하다는 것이 여러 논문을 통해 입증되었다[8,9]. 하지만 아래와 같은 두 가지의 문제가 있다.
1) 수치적 안정성이 떨어진다. 3차 보간식의 특성상 격자점 사이의 값을 벗어나는 범위로 보간이 되면 시뮬레이션 시스템이 점차로 불안정해지는 원인이 될 수 있다.
2) 물리량이 보존되지 못한다. 수치소산으로 인한 물리량의 감소는 앞서 기술한 천수방정식에서 높이값 η의 손실을 가져오며, 결과적으로 물의 총량이 서서히 줄어들게 된다.
Unsplit Semi-lagrangian CIP(USCIP)법은 2008년 Kim등[9]에 의해 제안된 방법으로, 2차원 이상의 격자에서 기존의 CIP 다항식은 주어진 미분값들의 정보를 완전히 활용하지 않고 있다는 점에 착안하여 여기에 새로운 항을 추가함으로써 나머지 미분값들을 반영하는 방법이다.
Figure 4에서 보듯이, 4개의 2차원 격자점에서 우리는 물리량 ϕ와 그 x,y 방향으로의 편미분값을 사전에 알고 있다고 가정하면, 이 값들을 근거로 연립방정식을 세워 식(19)에서 제시된 2차원 CIP 다항식의 계수를 아래와 같이 구할 수 있다:
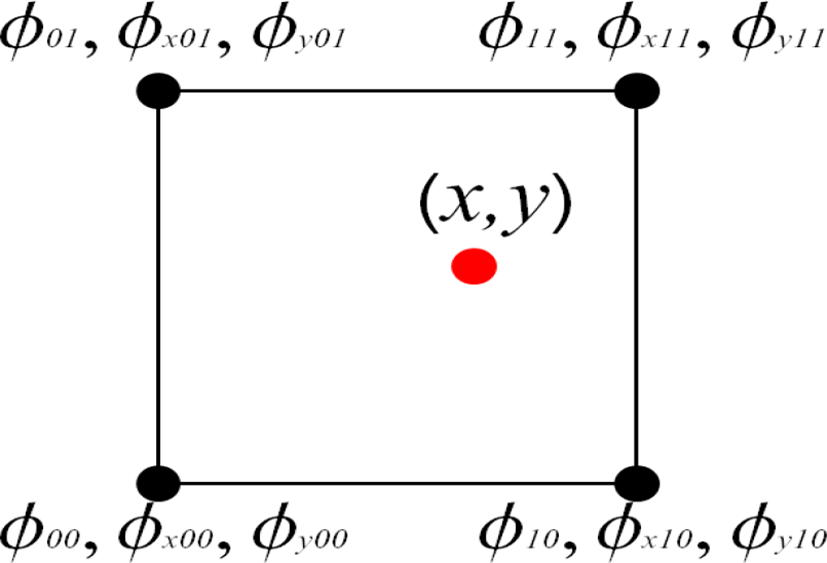
CIP 다항식의 개수는 10개이므로 계수 또한 10개를 구해야 하지만, 우리는 12개의 값을 알고 있으므로 이를 반영하기 위해 기존의 다항식에 2개의 항을 더 추가할 수 있다.
추가적인 항의 차수를 위와 같이 선택한 이유와 계수의 값은 해당 논문에 구체적으로 서술되어 있다[9].
적분값을 이용한 CIP법은 Yabe 등이 CIP-CSL(CIP-Conservative Semi Lagrangian)법[12]을 최초로 제안하였다. CIP-CSL법은 격자 구간 사이의 체적을 보간 정보로 활용함으로써 물리량을 보존하는 방법이다. 1차원의 경우, 적분값이 추가되므로 보간식은 4차로 구성되며, 다섯 개의 항이 필요하다:
격자 간격이 1로 정규화 되어있을 경우, 주어진 다섯 개의 프로파일을 이용하여 계수를 구하면 다음과 같다:
한편, 적분값은 해당 격자를 통과하는 유량(flux)에 따라 갱신된다.
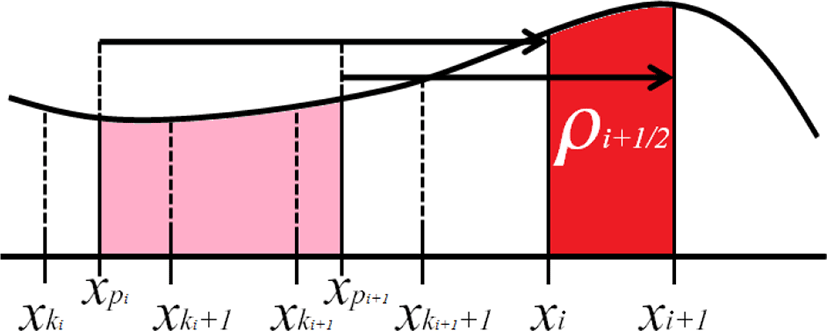
적분값 갱신에 필요한 유량은 Semi-Lagrangian으로 구한다. Figure 5와 같이 먼저 격자점의 위치를 되추적한 다음, 해당 범위 내의 적분값을 가져오면 된다. Figure 5에서, 다음 타임 스텝의 유량 은
이 된다. 편의상 CFL수치, 즉 uΔt/Δx<1이라고 가정한다면 구해지는 적분값은
으로 표현할 수 있다.
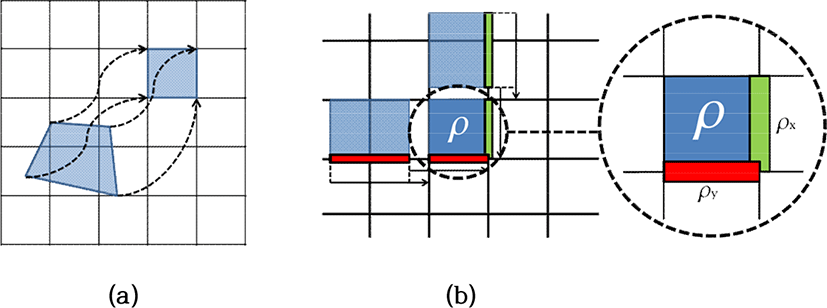
2차원의 경우, Figure 6:(a)와 같이 각 격자점을 추적했을 때, 적분되는 영역의 형태가 비정규적으로 나타난다. 이와 같은 형태로 나타나는 적분 영역은 바로 구할 수 없기 때문에 차원분할(dimensional splitting)과정이 필요하다. 즉, Figure 6:(b)와 같이 격자점의 경계면에 1차원 적분값을 저장하고, 각각의 방향 별로 들어오는 유량을 계산하는 것이다.
차원 분할은 각각의 방향 별로 격자점의 위치를 하나씩 되추적 한 다음 이에 대해 적분 연산을 수행하므로 높은 계산 비용이 필요하다. 이를 절감하기 위해 본 논문에서는 Conservative USCIP(CUSCIP)라고 명명한 새로운 CIP기법을 제안한다. 앞서 살펴본 바와 같이, Kim은 Yabe가 최초 제안한 CIP다항식에 차수가 대칭(Symmetric)이면서도 최소의 차수를 갖는 2개의 항을 추가하였다. 본 논문에서 제안하는 방법은 여기에 대칭을 유지하는 또 다른 항 C22x2y2를 아래와 같이 추가한다:
이로써 다항식은 13개의 항을 가지게 되며, 4개의 격자점과 그 중앙에 저장된 13개의 보간 정보로 계수를 구할 수 있다.
ϕ와 ϕx, ϕy는 Semi-lagrangian기법과 동일한 방법으로 갱신하며, 적분값 ρ는 현재 타임스텝의 값 ρn으로부터 명시적(explicit)으로 이동한다.
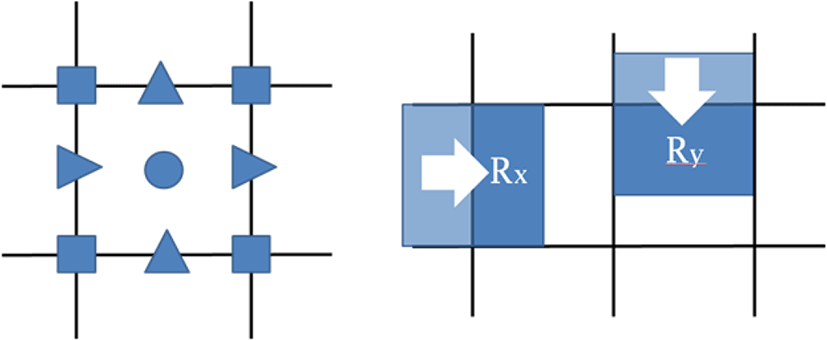
Figure 7과 같이 정사각형 모양의 적분 영역이 이동했다면, 적분값 ρ가 이웃 격자 영역으로 유입되는 각각의 유량(flux)은 Rx, Ry 영역의 물리량을 각각 이중 적분함으로써 구할 수 있다.
이와 같이 각 영역별로 나누어진 적분값을 해당 격자의 Δρ로 사용하면, 모든 격자점의 ρ값을 갱신할 수 있다. 이 방법을 사용하면 모든 영역에 걸쳐 적분 값을 감안하므로 물리량을 보존할 수 있으며, 또한 차원 분할 과정이 생략되므로 계산 시간이 절감된다. 또한, 기존의 USCIP에 적분값이라는 보간 정보를 하나 더 추가하기 때문에 보다 정확한 결과를 얻을 수 있다.
5. 실험 결과
본 논문은 인텔 i7 4.2GHz CPU 32GB RAM, NVIDIA GeForce GTX 1080 하드웨어 환경에서 구현하였다. 시뮬레이션은 CPU에서 연산되며, 2차원 물결 렌더링은 GPU에서 연산되도록 하였다.
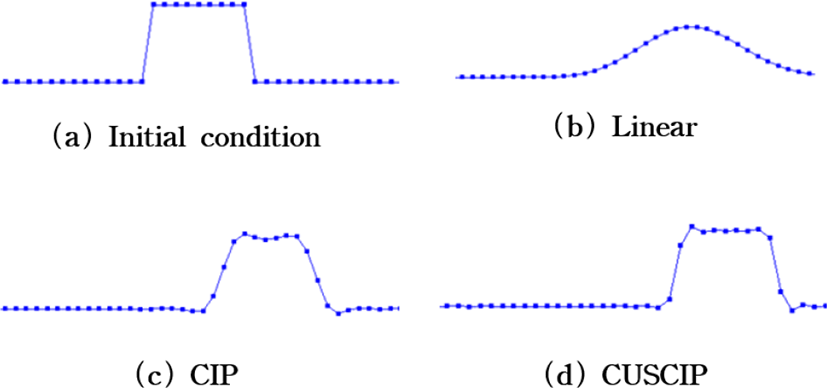
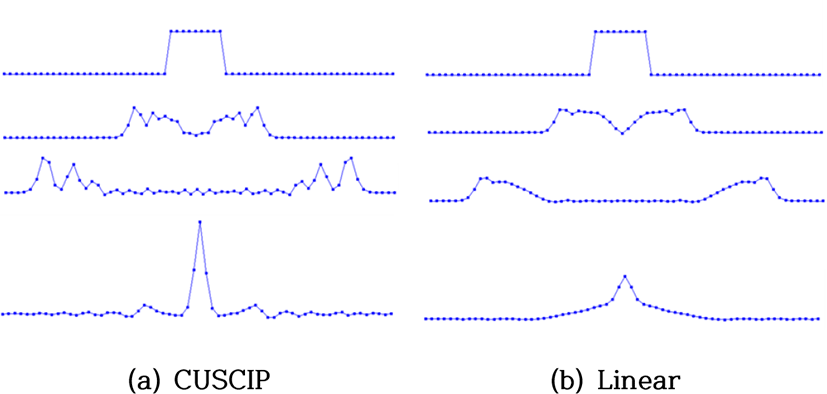
본 논문에서 사용한 방법의 정확도를 검증하기 위해, 고정된 속도장을 따라 움직이는 1차원 대류식을 푸는 과정을 시각화하였다(Figure 8).
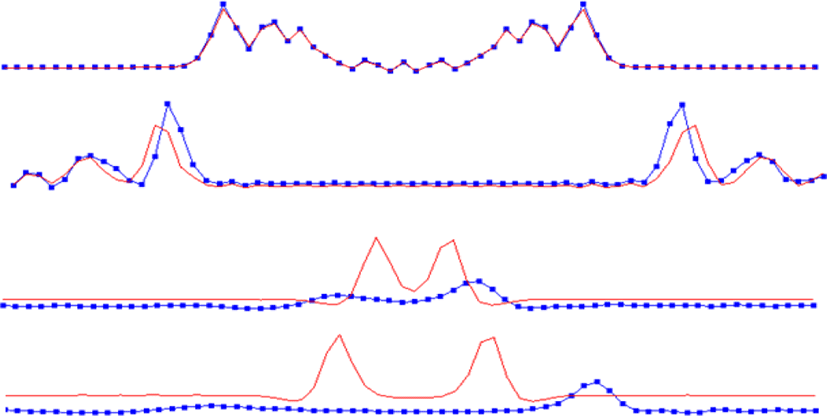
선형 보간 모델에 비해 CIP와 CUSCIP는 초기조건의 수치적 소산이 없음을 확인할 수 있었다. 게다가 CUSCIP는 제약조건으로 적분값을 추가하였으므로 셀 단위의 물리량이 보존됨을 확인할 수 있었다.
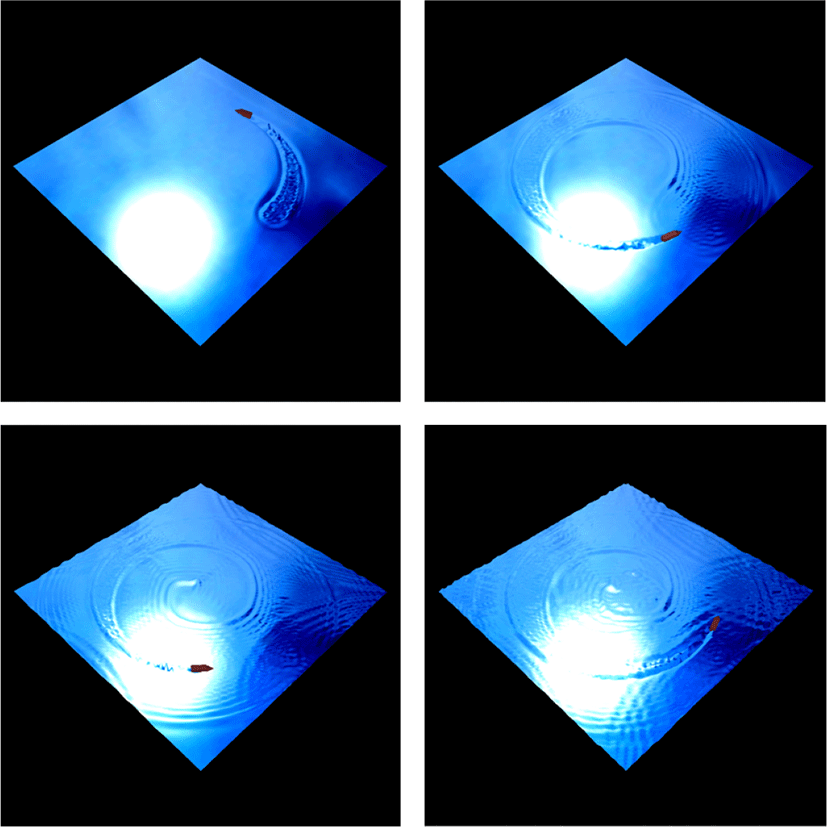
다음 실험으로 1차원 천수방정식으로부터 물의 파동을 시뮬레이션 하였다. Figure 9에서 CUSCIP의 경우, 선형 모델보다 월등히 수치소산이 적음을 확인하였다. CUSCIP와 CIP를 직접적으로 비교한 결과(Figure 10), CUSCIP는 CIP보다 물결의 더 오래 지속되고 높이값의 총량도 유지됨을 확인할 수 있었다. 2차원 천수방정식의 시뮬레이션 결과는 GLSL을 이용하여 렌더링 하였으며, 모두 실시간으로 구동된다(Figure 11과 Figure 12 참조). 시뮬레이션 해상도가 높지 않은 환경에서도 CUSCIP 방법은 상세한 물결의 움직임, 즉, 높은 주파수의 물결까지 표현할 수 있음을 확인하였다.
6. 결론 및 향후 연구
이 논문은 천수에서 물결의 세부묘사를 표현하면서 물리량은 보존할 수 있도록 하는 CUSCIP 방법을 개발하였다. 본 논문에서 제시한 방법이 천수방정식의 높이값 보존을 위해 시작된 것이기는 하지만, 활용적인 측면에서 천수방정식으로 한정할 필요는 없다. 물리량의 보존은 모든 유체 시뮬레이션에 필요한 특성이므로 해당 논문의 방법을 일반화하여 모든 유체로 확장하는 것은 중요한 연구 방향이 될 것이다.
본 논문에서 제시한 CUSCIP 방법의 한계는 상당히 큰 시뮬레이션 시간 간격이 제시될 경우, 시뮬레이션 안정성이 보장되지 못한다는 점이다. 이는 격자점의 값을 넘어서 적분값을 가져오게 되며, 각 격자에서의 물리량의 보존을 강제하기 위해 불필요한 진동이 생길 수 있다. 물론 적절한 시간 간격에서의 시뮬레이션을 수행할 경우는 수치적인 안정성은 보장된다.