1. Introduction
Mandibular canal detection in Computed Tomography (CT) data is a fundamental task for dental implant surgery. Most research has been conducted to improve upon the efficiency of this task. Tognola et al. [1] used the Snake method which required an initial contour around the mandibular canal. Kim et al. [2] proposed an automatic canal detection algorithm based on the Dijkstra method. And Llorens et al. [3] suggested fuzzy connectedness approach for automatic segmentation of mandibular canal. However, these methods depends significantly on anatomical variations and qualities of the mandibular canal on CT images. Fig.1 highlights difficulties with detecting the mandibular canal. The mandibular canal has many openings and ambiguous boundaries (see Fig. 1b), as well as high shape variation between different patients, making most existing methods impractical for clinical purpose.
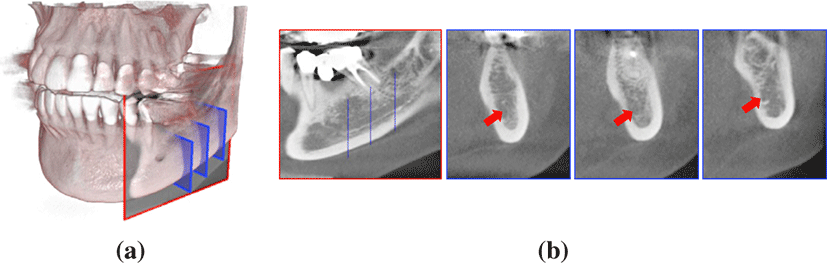
Dentists are prone to finding the sagittal plane where the mandibular canal path is well observed (see Fig. 1b), prior to manual detection of the mandibular canal, during dental implant planning. Inspired by this, we focus on automatic detection of the desirable sagittal plane, instead of detecting the mandibular canal. Our approach can be implemented in the context of automatic plane detection that finds a sectional plane of interest for identifying specific anatomical structures in 2D image. Recently, several deep-learning-based approaches have been introduced for automatic plane detection. Ryou et al. [4] presented the plane detection method for 3D ultrasound axial-images, from the perspective of a classification problem using convolutional neural networks (CNNs). However, this detection method is not suitable to detect a plane that has arbitrary orientation. Li et al. [5] suggested an iterative transformation network (ITN), which learns a relative transformation moving an input plane to the desired plane. However, their network tends to learn the desired plane by large-scale anatomical structures rather than small anatomical structures, such as the mandibular canal path. In particular, the mandibular canal has long and narrow shapes, which means displaying the canal in a 2D sectional image is very sensitive to the plane transformation. Thus, the ITN is inadequate for finding the desired plane that displays the mandibular canal path.
In this study, we develop a deep-learning-based framework that combines two main techniques: 1) a modified version of the ITN method for detecting initial planes, and 2) a transformation optimization method, based on the CNN classifier, searching for optimal sagittal plane (i.e., the ground truth (GT) plane). In our framework, we first obtain N initial planes supposed to be located around the desirable sagittal plane, via N iterations of the ITN inference. Then, we search for the most desirable plane by exploiting the CNN classifier. Because the classifier provides a probability that a plane is similar to the GT plane in terms of the distribution of the mandibular canal path, we can select the best initial plane. We also define a cost function as a negative of the probability for the optimization process. Therefore, we can detect the desirable sagittal plane by minimizing the cost function with respect to the transformation. The main contributions of this paper can be summarized as follows. First, we present a deep-learning-based method for detection of the desirable sagittal plane; a fundamental task for mandibular canal detection prior to dental implant planning. Second, our approach outperforms the ITN method in terms of accuracy and convergence, achieving the robust, state-of-the-art performance for automatic plane detection. We believe that our method can improve the efficiency of dental implant planning and reduce the risk of surgical failure due to a clinician’s lack of experience. Furthermore, our approach provides the foundations for further mandibular canal detection algorithms.
2. Method
The ITN method [5] provides predictions for the desired plane via an iterative approach where the current prediction is derived from the previous ones. However, this method is limiting for accurately detecting the desirable sagittal plane, where the mandibular canal path is maximally observed. This is because the ITN is likely to be trained by large-scale anatomical structures (e.g., teeth, upper and lower jaws), rather than small-scale local structures such as the mandibular canal, from input plane image. Hense, the ITN provides the sectional planes that contain large-scale anatomical structures similar to the desirable sagittal plane. Notably, the sectional planes that have similar structures to the desirable sagittal plane are located close to the desirable sagittal plane. Therefore, the fine searching method can find an optimal plane from the initial plane, with the CNN classifier, a good tool for fine searching.
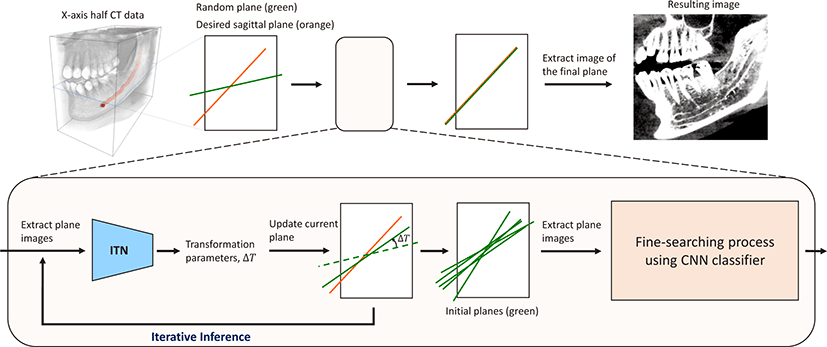
Fig. 2 illustrates an overview of the proposed method. This consists of two main techniques: 1) initial plane detection by using a modified version of the ITN method, and 2) a fine searching process for the desirable sagittal plane detection based on the CNN classifier. We first obtain planes via iterative inference of the ITN (see Algorithm 1). The planes are close to the desirable sagittal plane and serve as initial planes for the optimization. Subsequently, we detect the desirable sagittal plane by utilizing the CNN classifier with the optimization process. The CNN classifier was chosen because it can be trained to recognize whether a sectional image with similar anatomical structures contains the mandibular canal path or not. Moreover, it provides probability that represents how much of the mandibular canal path is observed on the sectional image. The details are explained in the next subsections.
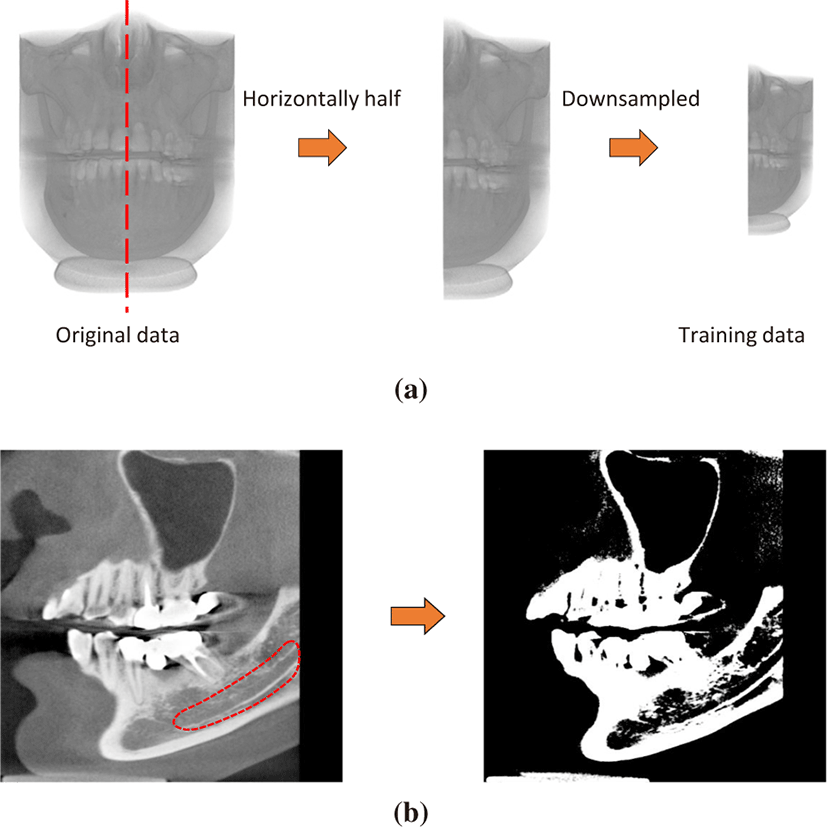
As the mandibular canals are located in both side jaws (left and right) symmetrically, we horizontally divide CT data into two half-ones and utilize each half as input data V. We resample CT data by 0.5×0.5×0.5 mm3 per voxel, which guarantees recognizing the canal path, for efficient processing. We also normalize CT values to the intensity range of the region surrounding the mandibular canal, such that our networks can capture the geometric features of the mandibular canal effectively. Fig 3 illustrates the scheme of training data generation.
Initial plane detection via ITN
1: procedure GET_INITIAL PLANES(V) ⊳ V : A half-side CT data
2: T0 ← Random transformation
3: M ← ∅
4: fori = 0 to N − 1 do
5: Xi ← I(V, Ti) ⊳ Sample plane image
6: ΔT ←ITN(Xi) ⊳ ITN predicts relative transformation
7: Ti+1 ← Ti · ΔT ⊳ Calculate new plane transformation
8: M ← M ∪ Ti+1 ⊳ Get new plane
9: OutputM
We generate plane data to train the ITN. The position and orientation of a plane is defined by 3D-rigid transformations (i.e., translation and rotation by quaternion units). To facilitate efficient training of the ITN, we consider three degrees of freedom (DOF) transformations for sagittal plane detection: 1) x-axis (sagittal) translation, 2) y-axis (coronal) translation, and 3) z-axis (axial) rotation. We fix x and y-axis rotation to zero, and fix z-axis translation to the vertically middle position of head bone, associated with a bone density of 1000 Hounsfield units (HU) [6]. We randomly sample a transformation T with respect to the 3-DOF. Then, rectangular plane images corresponding to sampled transformations are passed to the ITN, which learns 3-DOF transformations ΔT that locate input planes close to the desirable sagittal plane.
Algorithm 1 summarizes how we obtain the initial planes via the ITN inference. The ITN predicts a transformation δT relative to the input plane. Hence, absolute transformation Ti+1 for new plane is computed by compositing the input plane’s transformation Ti and δT, and is stored to transformation set M for initial planes. We repeat this process until N initial planes are obtained. It is noted that the initial planes have small variations in translations and rotations around the desired sagittal plane. This is an important property that the following CNN-classifier can provide optimal transformations for, detecting the desirable sagittal plane.
The CNN classifier is trained to learn 2D plane image classifications. The network is composed of a VGG-16 backbone and a last classifier that has two classes; class1 where images show the mandibular canal path well, and class2, which encompasses all other images. The fully connected layers are substituted with the convolutional layers, which improves computational efficiency and makes the network easier to train [7]. And we initialize weights of the last classifier with random values, and weights of other layers with pretrained weights from ImageNet [8]. Because the low-level features of natural images are similar to those from medical images, pretrained weights from ImageNet can be used to boost generalization performance of the network [9].
To ensure efficient and accurate training of the CNN classifier, we generate 2D plane images with small transformation variations from the GT plane, on CT datasets. The sampling scheme and CT datasets are the same as discussed in the previous subsections. And we remove the upper part of the plane images because mandibular canals are located inside lower jaw. This enables the CNN to focus on a smaller image area: the lower jaw where the mandibular canals exist. And we divide the plane images into two classes: one with a long canal path, the other without a canal path. Subsequently, we train the CNN classifier with these plane images. The CNN classifier is first used to select one initial plane with the highest class1 probability, from N initial planes generated by the ITN process. The selected plane can be used for a reliable initial plane for the following optimization process.
The selected initial plane is located around the desirable sagittal plane. The CNN classifier provides a probability measuring how close the input plane image is to the GT image in terms of the distribution of the mandibular canal. These properties allow for the fine searching of the desirable sagittal plane, based on the local optimization method.
We can find the desirable sagittal plane by minimizing the cost function C with respect to the 3-DOF transformation T.
where the cost function is defined as the negative of the class1 probability of the classifier, µ is a set of 3-DOF transformation parameters, and Tµ indicates the parameterized transformation. I(V, T) refers to the plane image, with transformation T from a half-side CT data V (see Section 2.1). To solve (Eq.1), we employ the iterative optimization approach [10] represented by
In every iteration k, transformation parameters µk are updated along the search direction dk (Eq. 2), where the search direction is the derivative of the cost function with respect to the k-step transformation parameters, and sk is a step size that controls the movement along the search direction. Starting with transformation parameters of the selected initial plane, the parameter updates are iterated until the cost function reaches a local minimum. Because the combination of the ITN and CNN classifier provides a good initial plane close to the GT plane, this local optimization approach can result in the desirable sagittal plane.
3. Experiments
We conducted several experiments to evaluate our method. First, we analyzed the effectiveness of transfer learning to achieve the best performance of the CNN classifier. We also compared our method to the ITN method in terms of the following metrics: 1) Euclidean distance (δt) between center positions of the predicted plane and GT plane, 2) rotation angle (δθ) between orientations of the predicted plane and GT plane, and 3) Canal Region Ratio (CRR) estimated by the ratio of the number of mandibular canal pixels of the predicted plane and GT plane. We tested 40 cases from 20 dental CT datasets; our reasoning for which was discussed in Section 2.1. For experimental evaluation, dental experts performed manual operations, generating desirable sagittal planes where the mandibular canal path is well observed, and also segmenting the mandibular canal in pixels.
All experiments were implemented using the Tensorflow framework, with an Intel i7 7700 CPU and NVIDIA TITAN V GPU. We configured the ITN with three convolution layers, where each convolution layer is followed by an average pooling layer. At the end of the last pooling layer, we added fully connected layers identical to those from the original ITN [5]. All weights of the network were randomly initialized, before we trained the network by using the Adam optimizer, with learning rate=5×10−4, β1=0.9, β2=0.999, ε=0.01, and a batch size of 128. We set the iteration number N to 10 for gathering initial planes, as discussed in Section 2.2. To select the best CNN classifier, we compared two popular CNN architectures such as VGG Net [11] and ResNet [12] with different layer-depth and training models.
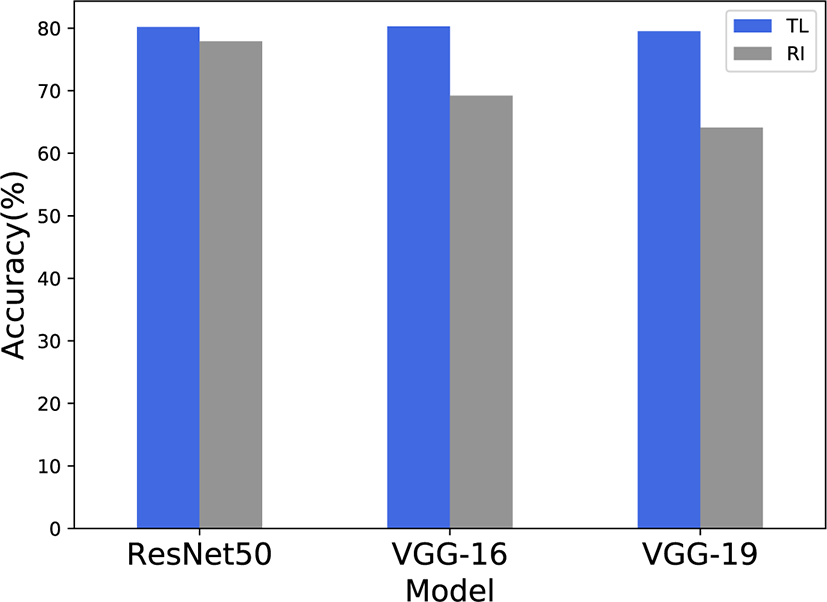
We experimented with three typical CNN backbone networks (ResNet50, VGG-16, VGG-19) with two different training models (random initialization (RI), or transfer learning (TL) from the ImageNet-pretrained model) to select the best CNN classifier for our fine searching process. For the performance evaluation of the CNN models, we used 500 images in both class1 and class2; generated as discussed in Section 2.3. The classification accuracy of each CNN model is shown in Fig 4. In our experiment, the TL training models achieved better accuracy than the RI training models. This demonstrates that transferred knowledge from natural images is effective for the recognition of the mandibular canal in CT images. In our experiments, VGG-16 with TL network model yielded the best results. Thus, we employ the VGG-16 TL model for the CNN classifier used in our fine searching process.
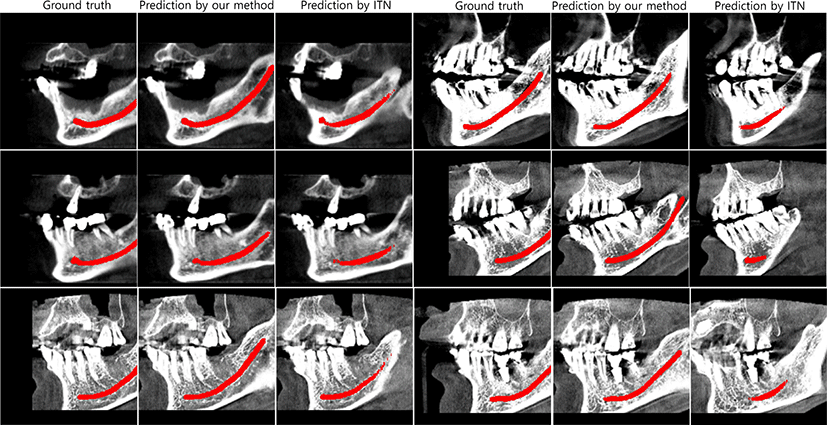
We compared the proposed method with the original ITN method for the sagittal plane detection on 20 CT datasets of different patients. Table 1 shows that our method can provide more satisfactory results compared to the stand-alone ITN method, in terms of lower plane detection errors (δt and δθ), and higher CRR values, which correlate to higher observation levels of mandibular canals. This demonstrates that our fine searching process, based on the CNN classifier, works effectively combined with the ITN. Fig. 5 displays the GT plane alongside the sectional planes predicted by our method and the ITN method, respectively. This proves visually that our method can be effectively used for detecting the desirable sagittal planes, where the mandibular canal path is maximally observed.
| Method | δt(mm) | δθ(°) | CRR |
|---|---|---|---|
| ITN | 9.79±7.00 | 1.75±1.29 | 0.539±0.377 |
| Ours | 9.73±6.40 | 1.32±0.869 | 0.886±0.149 |
4. Conclusion
In this work, we have presented a deep-learning-based method to detect the sagittal plane, which allows best observation of the mandibular canal. This is accomplished by combining a modified ITN model and the CNN classifier. The ITN model provides good initial predictions for the desired sagittal planes in terms of anatomical similarity, which means that the predicted planes are likely to be located close to the desirable sagittal plane. The CNN classifier can be used to find results closest to the GT plane, based on our optimization process with the initial predictions. Our method can achieve more satisfactory results compared to the stand-alone ITN method, which is a standard plane detection technique. This improvement in performance is measured in terms of the Canal Region Ratio, that indicates how much the mandibular canal is observed in the predicted plane relative to the GT plane, and by the transformation difference between the predicted plane and GT plane. This demonstrates that the proposed method can alleviate the burden on dentists detecting the mandibular canal path via manual operation, reducing the likelihood of surgical errors and decreasing the detection time. Hence, we believe that our proposed method can be used as a foundation for future work on automatic mandibular canal detection algorithms.