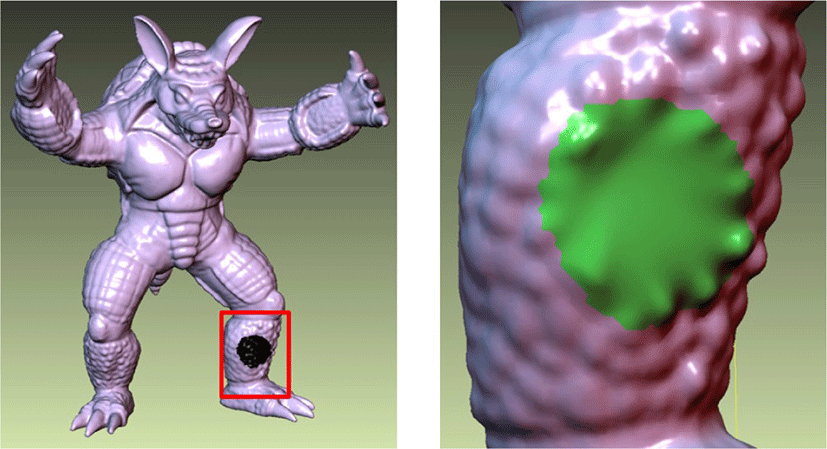
1. 서론
삼각 메쉬는 형상에 대해 일반적이고 유연하며 곡면 표현을 위 한 쉽고 효율적 인 수단으로써 컴퓨터 그래픽스,기하 모델링 에서 널리 사용된다. 실제 물체로부터 삼각 메쉬를 만들어 내는 것은 컴퓨터 그래픽스에서 중요한 과제이다. 일반적으로 스캔 장비를 이용하여 물체의 표면을 샘플링하여 포인트 클라우드를 얻는 방식이 많이 사용된다. 실제로는,물체의 표면이 빛을 반사하는 성질,오클루전(occlusions), 접근성의 한계 등과 같은 문제들 때문 에 물체의 표면은 완전히 샘플링되지 않는다 [1]. 이렇게 얻어진 메쉬는 아티팩트(artifact) 또는 원치 않는 홀을 가지고 있을 수 있다. 이런 불완전한 메쉬는 때로 어플리케이션에 직접적으로 사용 될 수 없다.
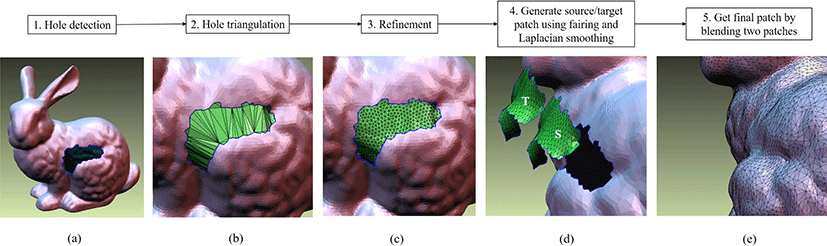
불완전한 메쉬를 수리하거나 원치않는 홀을 채우는 것은 컴퓨 터 그래픽스에서 곡면 복원을 하기 위한 중요한 문제이다. 일반적으로 메쉬 홀 채움의 목표는 주변 메쉬와 부드럽게 연결되며 원래 모델과 잘 어울리는 홀 패치를 생성하는 것이다. 하지만 홀의 복잡성 때문에 만족스러운 홀 패치를 만들어내는 것은 쉽지 않은 문제이다. 본 논문에서는 빠르고 효율적으로 동작하는 새로운 홀 채움 알고리즘을 제시한다. 알고리즘은 여러 단계를 거쳐 진행된다(Figure 1 참조). 첫번째,메쉬의 홀을 검출하고,두번째,삼각화,세분화,공정화 과정을 거쳐 타겟 패치를 생성하고, 타겟 패치를 스무딩하여 소스 패치를 생성한다(Section 3). 마지 막으로,패치간 형상 차이 기반의 블렌딩을 통해 최종 홀 패치를 합성한다(Section 4). 타겟 패치는 경계에서의 높은 연속성을 만족하며 주변 메쉬의 굴곡을 충분히 반영하고 있는 홀 패치이다. 이를 스무딩하여 생성한 소스 패치와 형상 차이를 분석하여 패 치간블렌딩을 수행하면 사용자가 원하는 수준의 홀 패치를 얻을 수 있다. 제안된 삼각 메쉬흘 채움 기법은 다음과 같은 장점을 가진다.
-
홀의 크기가 크더 라도, 삼각화 과정 이 단순하기 때문에 알고리즘이 빠른 시간내로 수행된다(Figure 9 참조).
-
공정화 과정으로 인하여 임의 모양의 홀에 대해서도 강건하게 작동한다(Figure 10(d) 참조).
-
소스와 타겟 패치 사이의 형상 차이를 고려함으로써 주변 메쉬와 어울리고 특징이 더욱 향상된 홀 패치를 얻을 수 있다.
2. 관련연구
지금까지 다양한 메쉬 홀 채움 알고리즘이 개발되어 왔다. Barequet 등 [2]은 메쉬에 존재하는 홀 또는 갭(gap)을 채우기 위해 최소 면적 삼각화(minimum area triangulation)방법을 찾기 위한 동적 프로그래밍 방식을 사용했다. 이 방식은 다른 많은 메쉬 리 페어(repair) 알고리즘의 기반이 되었다 [3]. 그러나 홀 경계에서 의 부드러움은 고려하지 않으며 거친(rough) 홀 패치를 생성한다는 점에서 제한적이다. Pfeifle 등 [4]은 조각 다항식 곡면(piece-wise polynomial surfaces)에 존재하는 홀을 채우기 위해 들로네 (Delaunay) 삼각분할을 이용한 세분화와 공정화 기법을 사용하여 부드러운 홀 패치를 생성했다. Liepa 등 [5] 또한 홀을 채우기 위해 삼각화, 세분화를 사용했고 더 나아가 홀 패치의 삼각형의 밀도를 주변 메쉬와 비슷하게 했다. 홀 패치를 공정화시키기 위해 umbrella 연산자를 제안했지만 삼각화 과정에서 O(n3)성능 때문에, 크기가 큰 홀의 경우에는 시간이 오래 걸리는 한계점이 존재한다. Chen 등 [6, 7]은 날카로운 부분에 의존적인 홀 채움 접근법을 제안했다. 그들은 방사형 기저 함수(radial basis function) 에 기반한 보간법을이용하여 초기 음함수 패치를 생성하고 만약 홀 경계에 날카로운 특징이 존재한다면 홀 패치에 베이즈 분류법 (Bayesian classification) [8]과 날카로움 의존 필터(sharpness dependent filter) [9] 기반의 특징 향상 과정을 적용한다. 그러나 날 카로움에 의존적인 필터에 사용되는 매개변수에 따라 홀 패치의 형상이 크게 달라진다 [10].
홀 패치를 주변 메쉬와 부드럽게 연결되도록 하는 기법 또한 연 구되어 왔다. Zhao 등 [11]은 AFM 기법 [12]을 적용함으로써 곡 률이 큰 홀을 채우는 초기 패치를 생성하고, 디리클레(Dirichlet) 경계 조건을 만족하는 포아송(Poisson) 방정식 [13]을 사용하여 홀 패치의 정점을재배치했다. Pernot 등 [14]은 들로네 삼각분할을 사용하여 초기 홀 패치를 생성하고, 주변 메쉬와의 블렌딩 조건을 만족시키면서 패치의 정점을재배치했다. 하지만 그들의 방식은 곡률이 큰 홀을 채우는 데에는 적합하지 않다. Branch 등 [1] 과 Xiao 등 [15]은 경계 주변의 이웃 정점을 샘플링하고 방사형 기저 함수(RBF)를 사용하여 홀 패치를 생성했다. RBF 기반의 형 상 복원은 간단하며 유용하지만 새로 생성되는 홀 패치가경계의 컨벡스 헐(convex hull)을 크게 벗어나지 않는다는 점에서 제한적 이다.
NURBS 곡면 또한 메쉬 모델의 홀을 채우기 위해 활용된다. Charles 등 [16]은 곡면위의 다각형 홀을 채우기 위해 C1 3차 스 플라인 패치를 사용했다. Li 등 [17]은 특징을 보존하는 홀 채움 알고리즘을 제시했다. 그들의 방식은 메쉬 홀 경계에서 불완전한 특징 곡선들을 찾고, 특징 곡선들을 잇기 위한 다항식 블렌딩 곡 선을 생성한다. 마지막으로, 특징 곡선으로 나뉘는 두개의 홀을 채우기 위해 베지에-라그랑주 혼합 패치(Bezier-Lagrange hybrid patch)를 구성한다. 이 방식은 홀 경계에서의 높은 연속성을 보 장한다. Wang 등 [10] 또한 특징을 보존하기 위한 방식에 초점을 맞추었다. 그들은 소실된 코너와 날카로운 에지를 복원하기 위한 특징 보존 홀 채움 프레임워크를 제시했다. Fortes 등 [18]은 곡면 복원과 병렬 또는 직교 곡선의 네크워크를 기반으로 한 홀 채움 구조를 제시했다.
3. 두 개의 패치 생성
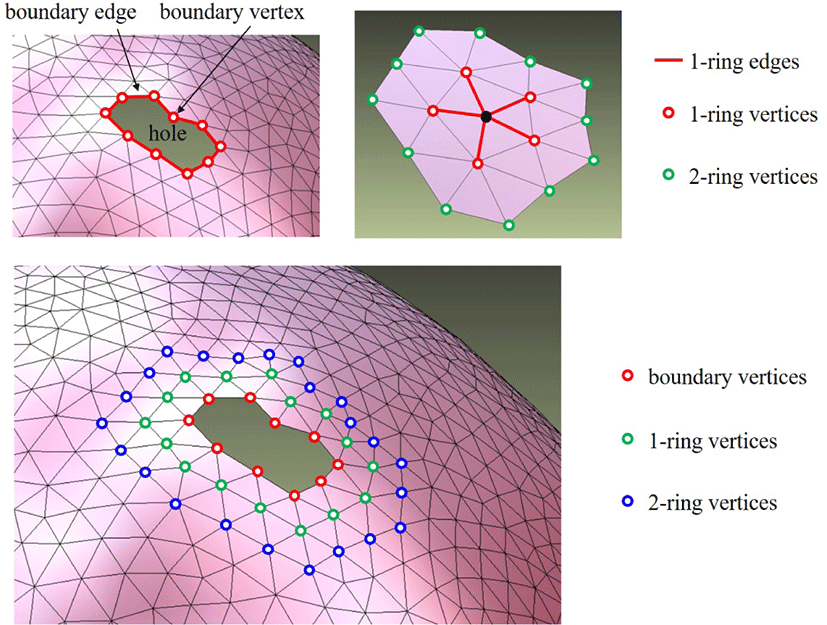
오직 한 개의 인접한 삼각형을 갖는 에지를 경계 에지라고 부른다. 만약 정점에연결된 에지들 중 경계 에지가 존재한다면 그 정점은 경계 정점이라고 부른다. 홀은 경계 에지들로 이루어진 닫힌 경로이다. 한 개의 정점에 연결된 모든 에지들을 그 정점의 1-링 에지라고 부른다. 정점의 1-링 에지들이 갖는 정점들(자기 자신 제외)을 그 정점의 1-링 정점이라고 부른다. 2-링 정점은 1-링 정 점들 중 각 정점의 1-링 정점을 조사함으로써 구할 수 있다. 이와 유사하게, 경계의 N-링 정점 또한 구할 수 있다(Figure 2 참조). 알고리즘을위해 본 논문에서는 경계의 1, 2-링 정점을 살펴본다. 원래 메쉬와 홀을 채우는 메쉬는 각각 주변 메쉬와 홀 패치라고 부른다. 본 논문에서는 다양체(manifold) 메쉬만을 다룬다. 또한 삼각 메쉬를 표현하기 위해 Kettner [19]가 제안한 하프에지(half edge) 자료구조를 활용한다. 삼각 메쉬에 대한 하프에지 자료구 조는 메쉬의 기하학적 연결 정보를 실시간으로 빠르게 얻을 수 있다. 앞서 설명한 개념들을 이용하면 메쉬의 홀을 빠르고 쉽게 검출할 수 있다. 특히, Pernot [14] 등은 만족스럽지 않은 홀 패 치가 생성될 것을 방지하기 위해 홀을 채우기 전에 홀 경계를 다 듬었다. 하지만 본 논문에서 제시된 기법은 복잡한 홀을 다룰 수 있기 때문에 홀 삼각화를 위한 전처리 단계를 생략할 수 있다.
홀 검출이 완료되면, 홀에 완전히 맞는 초기 홀 패치를 생성하기 위한 삼각화 과정을 시작한다. 본 논문에서는 AFM 기법 [12]의 간략화된 버전을 사용하는데, 이는 다음과 같이 몇 가지 단계로 구성된다.
-
각 경계 정점에서 인접한 두 에지 사이의 가장 작은 각도를 찾는다.
-
하나의 에지를 추가하여 두 개의인접한 에지와 경계 정점을 포함하는 새로운 삼각형을 만든다.
-
새로 생성되는 모든 삼각형으로 홀 영역을 채울 때까지 과정 1과 2를 반복한다.
이 방식을 사용함으로써 우리는 복잡하고 곡률이 큰 경계에 꼭 맞는 패치를 빠르고 쉽게 생성할 수 있다. 새롭게 생성되는 패치 안의 삼각형들은 거칠지만, 이어지는 세분화 단계에서 이러한 문제점은 자동적으로 해결된다. Figure 1(c)는 거친 삼각형들을 규칙적으로 만든 결과를 보여준다.
초기 패치 메쉬의 품질 향상을 위해 세분화 과정을 진행한다. 경계 에지를 제외한 내부 에지들은 매우 길며, 삼각형들은 비등방성 성질을 갖는다. 우리는 이러한 문제점을 해결하기 위해 점진적 리메싱 알고리즘을 채택한다 [3, 20, 21]. Algorithm 1은 목표 에지 길이를 입력으로 취하고, 에지 분할, 에지 제거, 에지 플립, 정점 이동을 순차적으로 수행한다.
목표 에지 길이 l은 경계 에지의 평균 길이로 정하고, 세분화후 패치와 주변 메쉬를 병합하기 위해 경계 에지를 분할 후보에서 제외한다. 에지 분할 단계에서는 임계 길이 high보다 긴 에지를 분할한다. 에지 제거 단계에서는 임계 길이 low보다 짧은 에지는 제거하고, 만약 제거하여 임계 길이 high보다 긴 에지가 생성될 경우, 에지를 제거하지 않는다. 모든 에지 길이가 l에 근접하고 삼각형 밀도가 주변 메쉬와 비슷하며 규칙적인 삼각형을 가진 패치를 얻을 때까지 알고리즘을 반복 수행한다. 품질이 향상된 홀 패치는 공정화 단계의 입력으로 사용된다. Figure 3은 알고리즘의 반복 수행 결과를 보여준다.

세분화후홀 패치 정점의위치를 재조정하고 부드럽게 만들기위한 공정화(fairing) 과정을 시작한다. 공정화는 공정 에너지(fairness energy)를 최소화함으로써 곡면을 가능한한 부드럽게 만드는 기술이다. 최소화하려는 공정 에너지 함수에 따라 최종적으 로 원하는 곡면을 생성할 수 있다 [3]. 본 논문에서는 멤브레인 (membrane) 에너지, 씬플레이트(thin-plate) 에너지, 곡률 변화율 (curvature variation) 에너지중에서 곡률 변화율 에너지에 초점을 맞춘다.
매개변수 곡면 x(u, v) : Ω → S의 멤브레인 에너지는 다음식으로 표현될 수 있으며 디리클레(Dirichlet) 에너지라고도 불린 다:
여기서 xu = ∂x/∂u 이고 xv = ∂x/∂v이다. 곡면의 좌표 함 수 x(u, v)를 삼각 메쉬 정점의 좌표 x = (x1,…, xn)T 로 대체하고, 이산 라플라스-벨트라미(Laplace-Beltrami) 연산자를 사용함으로써 위의 연속적인 영역의 공식을 삼각 메쉬로 이산화한다. 따라서 미지의 정점의 좌표 x에 대하여 다음이산 라플라스 방정 식을 풀 수 있다:
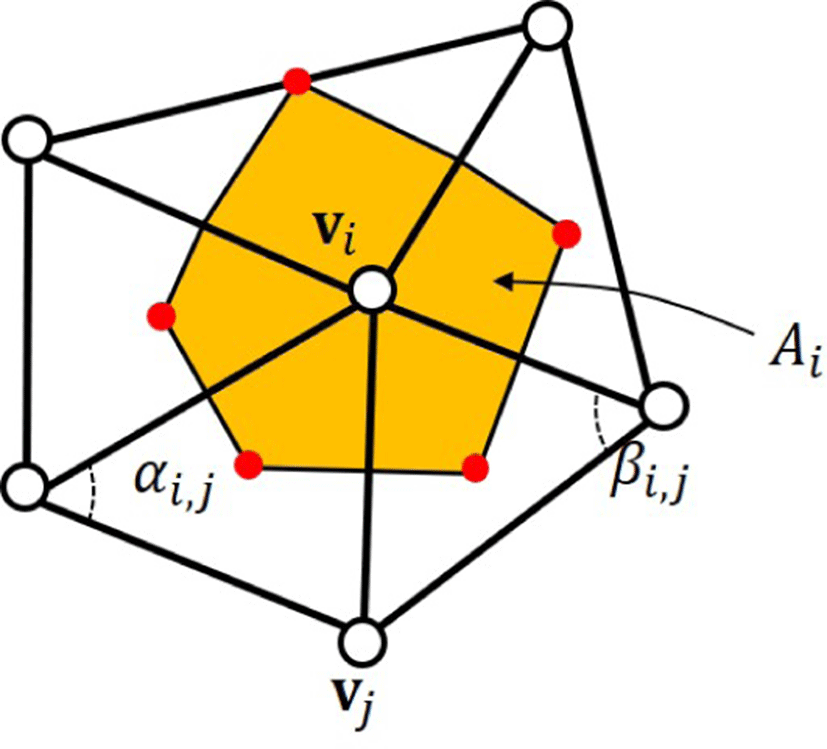
여기서 Δ는 이산 라플라스-벨트라미 연산자이며 x*는 경계 조건 ∂Ω을 만족하는 알려진 정점의 좌표이다. Figure 4에서 삼각 메쉬 위의 한 정점 vi를 공유한 n개의 삼각형을 가정하자. 국소 영역 [22] Ai를 갖는 vi에 대한 이산 라플라스-벨트라미 연산자는 다음과같이 정의된다:
f는 정점의 좌표의 x, y, z 성분 중 하나가 될 수 있다.
만약, 곡면의 곡률을 최소화하는 것이 목적이라면 다음 씬플레 이트 에너지 함수를 사용한다:
ẼTP(x)를 최소화 하기 위한 이산 라플라스 방정식은 Δ2x = 0, x |∂Ω = x* |∂Ω 이다. 또한, 곡률의 변화율이 최소화된 곡면을 얻기 위해 Moreton 등 [23]이 제시한 곡률 변화율 에너지를 사용할 수 있다:
여기서 κ1, κ2는 주곡률이고 t1, t2는 그에 대응되는 주방향이다. ẼCV(x)를 최소화 하기 위한 이산 라플라스 방정식은 Δ3x = 0, x |∂Ω = x* |∂Ω이다.
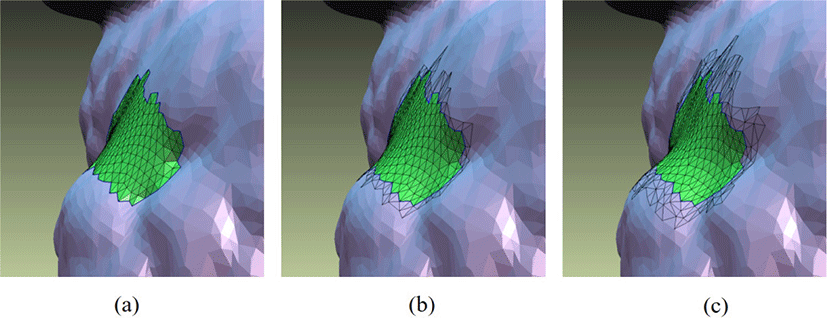
Figure 5은 홀 패치 메쉬의 공정화 결과를 보여준다. Figure 5(a) 에서는 홀 패치의 경계 정점들이 고정되어 C0 경계 조건이 만족 되고, Figure 5(b)에서는 경계 정점과 경계의 1-링 정점이 고정 되어 C1 경계 조건이 만족되고, Figure 5(c)에서는 경계 정점과 경계의 1, 2-링 정점이 고정되어 C2 경계 조건이 만족된다. 우리 는 이 중에서 주변 메쉬의 형상을 가장 잘 반영하는 곡률의 변 화율이 최소화된 곡면(Figure 5(c))을 블렌딩을위한 타겟 패치로 사용한다.
4. 홀 패치 블렌딩
메쉬 공정화를 통해 생성한 타겟 패치는 형상이 특징 표현이 두드러지지 못한 한계점이 존재한다. 때때로 주변 메쉬의 굴곡이 심한 경우에는 원하지 않는 형상의 홀 패치가 생성될 수 있다. 이러한 한계점을 극복하기 위해 본 절에서는 소스-타겟 패치간 형상 차이에 기반한 블렌딩을 제안한다.
타겟 패치에서 굴곡과 디테일이 충분히 제거된 소스 패치와 곡 률의 변화율을 최소화한 타겟 패치 사이의 곡률 및변위 즉, 형상 차이를 분석한다. 이러한 형상 차이에 기반한 블렌딩을 수행함으로써 굴곡이 더욱 강조되고 주변 메쉬와 어울리는 형태의 홀 패치를 사용자가 원하는 수준으로 얻을 수 있다.
소스와 타겟 패치 메쉬를 각각 S와 T 라고 하자. S와 T 의 형상 차이를 계산하기 위하여 각각의 메쉬에 대해 이산 곡률 분석을 할필요가 있다. 메쉬 위의 한 정점 vi 의 좌표가 xi일 때 vi 에서의 평균 곡률의 절대값 Hi 은 다음과같이 계산될 수 있다:
여기서 Δ는 이산 라플라스-벨트라미 연산자이다. 그리고 S 와 T 는 동일한 정점의 수와 연결 정보를 가지며 정점간의일대일 대응 관계가 성립한다. 대응되는 정점 vi 와 v′i 의 형상 차이는 다음과 같이 계산될 수 있다:
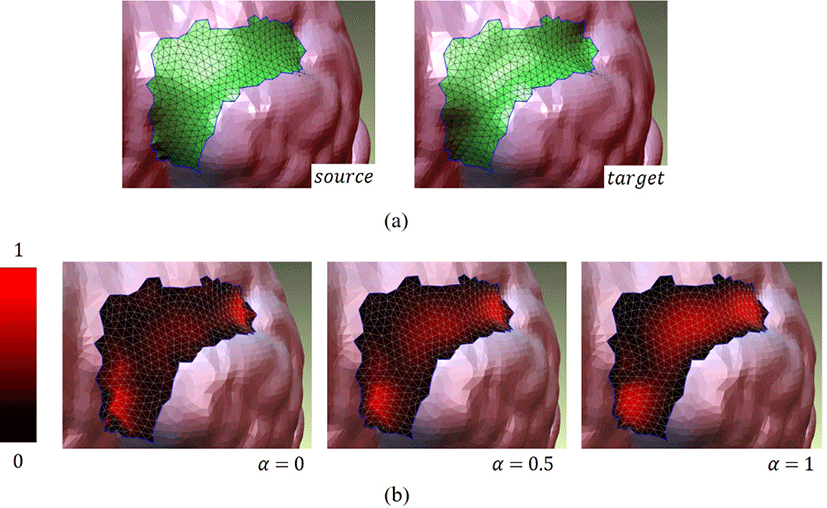
여기서 Δκi는 두 정점의 곡률 차이 이고, di는 정 점간 변위이다. 0 ≤ α ≤ 1는 사용자 정의 파라미 터이다. 만약 α = 0이라면 형상 차이는 오직 곡률의 차이에만 비례한다. 반면 α = 1이라면 형상 차이는 오직 변위에만 비례한 다. 사용자는 α를 조절함으로써 패치간의 형상 차이를 계산할 수 있다. Figure 6는 홀에서 생성된 소스-타겟 패치와 그 둘의 형상 차이를 컬러맵을이용하여 가시화한 결과를 보여준다.
소스-타겟 패치는 형상은 다르지만 모든 정점에 대해 일대일 대 응관계가 성립하기 때문에 형상 블렌딩이 가능하다. 제어 파라미터 w 에 따라 소스 패치 S 와 타겟 패치 T 사이에 다음 선형 블렌딩을 적용하면 새로운 패치 P 를 합성해낼 수 있다:
제어 파라미터 w가 0 ≤ w ≤ 1 인 경우, P 는 S 와 T 의 보간법 (interpolation) 의해합성된다. 반면 w < 0 또는 w > 1인 경우, P는 S와 T 의 보외법(extrapolation)에 의해합성된다. 본 논문에서는 제어 파라미터 w 를 정점별로 재매개화하여 변형 파라미터 를 정의하였다:
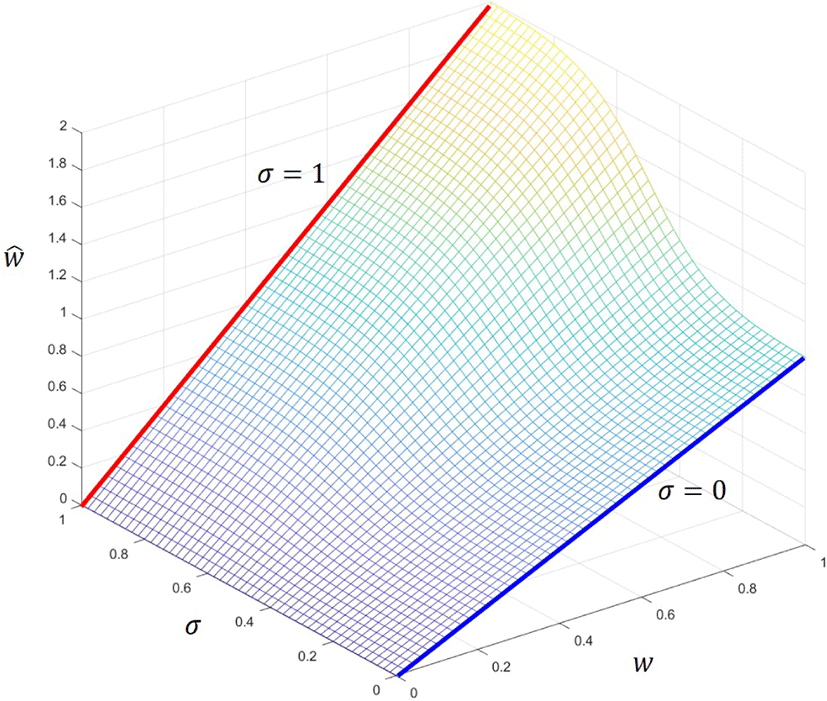
적절한 를 설정하기 위해 각각의 정점 vi에 대하여 패치 사이의 형상 차이 σi를 계산한다. 만약 형상 차이 σi가 크다면, 이는 정점 vi 주변에서 패치 메쉬의 형상의 변화가 크다는 것을 유추할 수 있다. 형상 차이가 큰 정점 vi는 상대적으로 홀 패치의 중요한 특 징을 표현한다고 해석 할 수 있다. 따라서 이러한 정점들은 변형 파라미터를 더 크게하여 블렌딩 과정에서 더욱 강조되도록 한다. 만약 한 정점에서 σi = 0, 즉 형상차이가 거의 없다면 변형 파라 미터 는 w와 같다. 반면 σi = 1, 즉 형상차이가 큰 정점에서는 = 2w이므로 소스-타겟간 형상 차이가 강조된다(Figure 7참 조).
5. 실험결과
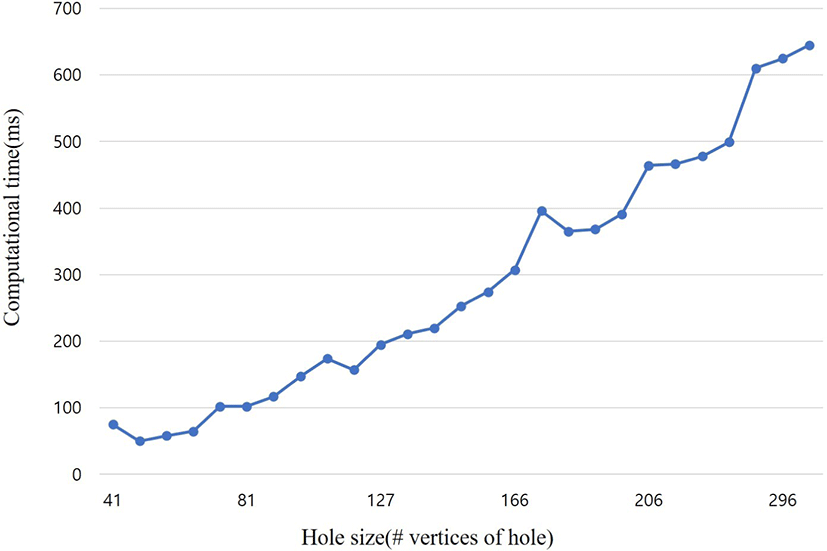
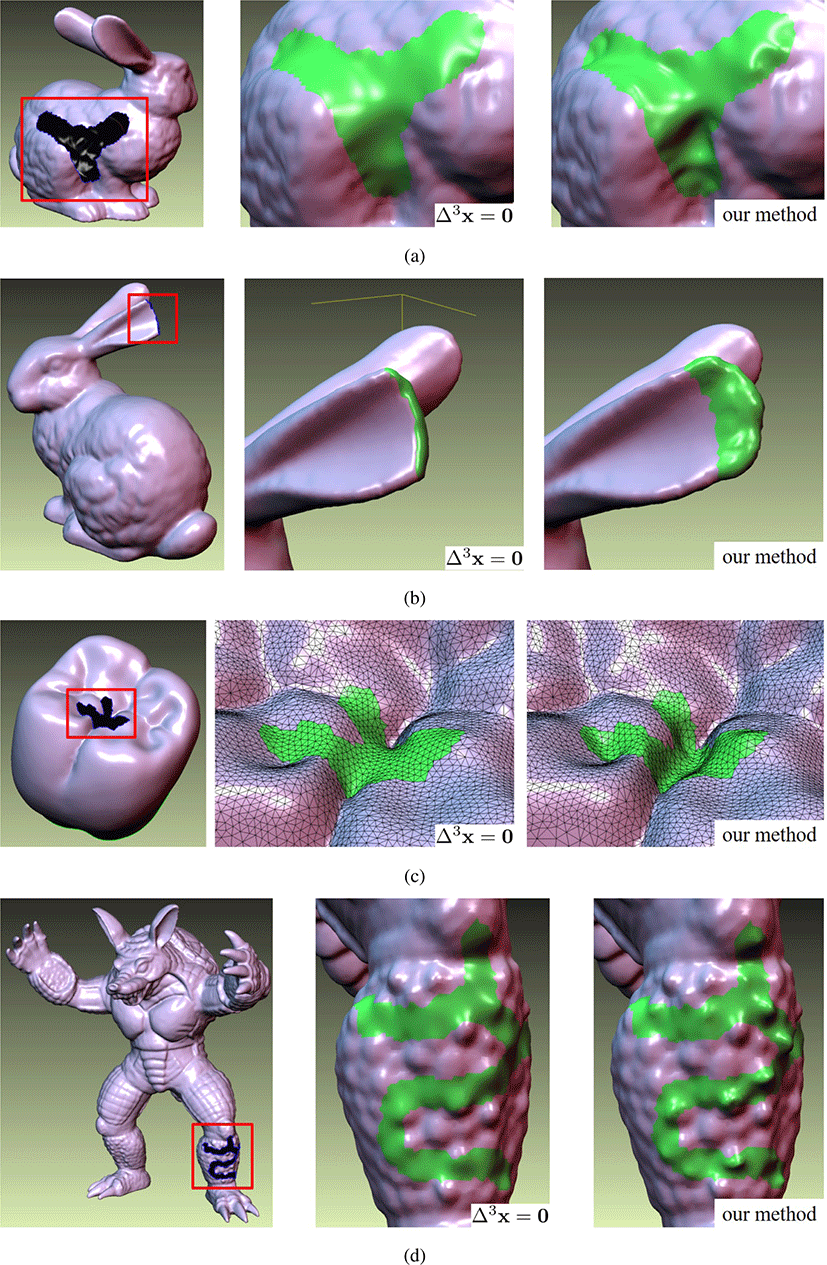
본 논문에서 제안한 형상 차이 기반 홀 채움 기 법은 C++ 언어를 사용하여 Intel i7-9700F CPU, 16Gb의 메 인메모리와 NVIDIA RTX 2060 그래픽 카드가 설치된 PC에서 구현되었다. 제안된 기법의 효과성을 실험하기 위해 다양한 홀을 가진 모델을 사용하였다. Figure 10은 각각의 모델에 대해서 최소 곡률 변화율 방식의 홀 채움 결과와 형상 차이 기반 블렌딩 방식의 홀 채움 결과를 비 교하여 보여준다. 본 논문에서 제시한 기법은 특히 주변 메쉬에 굴곡 및 특징 이 많이 존재하는 경우 이를 효과적으로 복원 가능하 다. Figure 10(a)에서는 α = 0.5로 설정하여 소스-타겟 패치간의 곡률과 변위를 절반씩 고려하여 굴곡을 과장시켰다. Figure 10(b) 에서는 토끼 모델의 귀 부근에 생성되는 소스-타겟 패치 사이의 변위를 크게 고려하였다. 따라서 변위가 큰 정점들은 블렌딩 과정 중 큰 폭으로 이동하여 부족한 귀의 형상이 복원되었다. Figure 10(c)처럼 움푹 패인 형상에 홀이 있는 경우 곡률과 변위를 충분히 고려하여 이를 복원하였다. Figure 10(d)에서는 생성된 소스-타겟 패치간의 곡률차가 심한 특성을 이용하여 홀 패치에 존재하는 돌기를 과장시키는 결과를 얻었다. Table 1은 홀의 크기를 늘려가면서 홀 패치를 생성하는 시간을 측정한 결과이고, Figure 9은 Table 1의 결과를 가시화한 결과이 다. 실험 결과에서 보듯이 메쉬의 홀을 이루는 정점의 개수에 따라 홀 패치를 생성하는 시간은 선형적으로 증가하는 것을 볼 수 있다.
| Hole size (# vertices of hole) | Time (ms) |
|---|---|
| 41 | 75 |
| 81 | 102 |
| 127 | 195 |
| 166 | 307 |
| 206 | 464 |
| 296 | 625 |
6. 결론
본 논문에서는 형상 차이 기반 블렌딩을 이용하여 삼각 메쉬의 홀을 채우는 기법을 제안하였다. 메쉬 홀을 채우는 소스 및 타겟 패치를 생성하여 그 둘의 형상 차이를 분석하였으며, 이를 기반한 형상 블렌딩을 통해 주변 메쉬와 어울리는 홀 패치를 사용자 가 결정할 수 있도록 하였다. 크고 다양한 홀을 가진 메쉬 모델에 대하여 제안된 기법을 적용한 결과, 기존 방식으로는 복원될 수 없었던 주변의 굴곡이나 특징 이 만족할 만한 수준으로 복원되는 결과를 얻었다.
제시된 방법은 공정화를 통해 생성한 패치를 블렌딩 타겟으로 선정했기 때문에 때로는 정점의 블렌딩 방향이 자연스럽지 못할 때가 있다. 또한 타겟 패치 생성 과정에서 주변 메쉬를 최대 2-링 까지만 고려하였기 때문에 주변의 더 많은 특징을 고려하지 못하 는 한계점 이 존재한다(Figure 8참조). 향후 연구에서는 생성 되는 홀 패치가 더 넓은 주변 영역의 디테일을 충분히 반영하도록 홀 채움 기법을 확장할 계획 이다.