1 서론
BCC 격자 (Body centered cubic lattice) 는 일반적으로 널리 사용되는 카티시안 격자(Cartesian lattice)에 비해 볼륨 데이 터를 좀더 효율적으로 저장할 수 있는 격자로 알려졌다.[1] 이러 한 BCC 볼륨 데이터의 등가면을 명시적으로 추출하기 위해서 가장 널리 사용되는 방법은 BCC 격자 고유의 사면체 구조(그 림 1b)에 마칭 사면체 기법(Marching tetrahedra, 이하 MT)을 적용하는 방법이다. 하지만 마칭 큐브 기법(Marching cubes, 이하 MC) 과 마찬가지로 이러한 기법을 적용해 얻은 등가면 데이터는 삼각형 집합 (Triangle soup) 의 형태로 표현되어 렌 더링이 비효율적이고 등가면의 연결정보를 얻을 수 없다는 단 점이 있다. 이를 해결하기 위해 등가면을 이루는 삼각형 정점들 의 좌표를 기준으로 중복을 제거하는 후처리 과정을 추가하여 연결된 메시 형태의 등가면을 추출하는 기법이 제안되었고[2] MT에도 쉽게 적용할 수가 있다. 하지만 이러한 후처리 기법은 연산량이 많아 전체적인 성능을 크게 떨어뜨린다는 단점이 있 다.
고전적인 마칭 기법들은 볼륨 데이터의 모든 영역에서 등가 면의 존재 여부를 검사하고 삼각형을 추출한다. 하지만 등가 면은 극히 일부분의 영역에서만 존재하기 때문에 이러한 방 식은 비효율적이고 이를 개선하기 위한 여러 방법이 제안되 었다.[3, 4] 본 논문에서는 기존에 제안했던 개선된 MC 기법 과 유사하게[5] BCC 볼륨 데이터로부터 메시 형태 (Triangle mesh) 의 등가면을 추출할 수 있는 실시간 GPU 기반의 마칭 기법을 제안한다. 본 기법은 볼륨 데이터를 BCC 사면체 구조 로 균일하게 분할하고, GPU에서 각각의 사면체에 효율적으로 접근할 수 있는 순번을 정의한다. 이를 통해 볼륨 데이터에서 등가면을 포함하는 BCC 사면체 구조를 추출하고, 이들로부터 각각 정점 버퍼(Vertex buffer)와 인덱스 버퍼(Index buffer)를 생성한다. 이 때 사면체들이 공유하는 엣지 (Edge) 에 대해서 중복된 등가면 검사가 수행되지 않도록 하여 연산의 효율성을 높이고 삼각형 메시 구조의 등가면을 추출할 수 있도록 하였다. 또한 Chen등이 제안한 기법을[4] 응용하여 BCC 격자에서 빈 공간을 생략하는 기법을 추가하였고, 이를 통해 보다 효율적인 등가면 추출이 가능하도록 했다. 실험 결과, 5123 이상의 고해 상도 볼륨 데이터에 적용하면 삼각형 집합 형태의 등가면을 추출하는 고전적인 BCC MT 기법에 비해서 추출되는 등가면 데이터의 크기를 50% 정도 줄이면서도 최대 5배 정도의 속도 향상을 보인다.
2 관련 연구
고전적인 MT 기법들은 카티시안 격자에서 등가면을 추출하 였다. Doi와 Koide[6] 그리고 Guéziec과 Hummel은[7] 볼륨 데 이터의 각 정육면체 셀을 5개의 사면체로 분할하여 MT를적 용하는 기법을 제안하였다. 한편 카티시안 격자가 아닌 다른 격자에서의 MT도 연구되었는데, Chan과 Purisima는[8] BCC 볼륨 데이터의 사면체구조에 MT를 적용한 기법을 제안하였 다. 이는 본 연구와 기본적인 방법은 같으나 등가면을 이루는 삼각형이 메시 형태가 아닌 점이 다르다. 그리고 Carr등은[9] BCC 격자의 구조를 활용하여 사면체/팔면체/육면체에 기반 한 다양한 마칭 기법을 제안하였다.
최근에는 GPU를 사용하여 실시간으로 등가면을 추출하는 방 법도 제안되고 있다. Tatarchuk 등은[10] 지오메트리 쉐이더 (Geometry shader)를 이용한 MT 기법을 제안하였다. 이 기법 은 각 정사면체 셀마다 8개의 볼륨 데이터 값을 읽어 등가면이 생기는지 판단한 후 필요한 경우 해당 셀을 6개의 사면체로 나 누어 각각 MT를 적용하여 등가면을 생성하였다.
다수의 마칭 기법들은 삼각형 집합 형태의 결과물을 생성하는 데, 이러한 데이터 구조는 삼각형 사이의 연결정보가 없고 중복 되는 정점 데이터로 인해 등가면의 곡률 계산과 같은 다양한 응 용에서 활용하기 어려운 단점이 있다. 이러한 단점을 보완하기 위해서 삼각형 메시 형태를 생성하는 마칭 기법들도 연구되었 다. Kim 등은[11] BCC 볼륨 데이터로부터 연결된 메시 형태의 등가면을 생성하는 MT 기법을 CPU(Central Processing Unit) 에서 구현하였다. Chen등[4]과 Liu등[12]은 본 연구와 비슷한 기법으로 연결된 메시 형태의 등가면을 생성하는 GPU기반의 MC 기법을 제안하였다.
마칭 기법의 연산 효율성을 높이기 위해 등가면이 존재하지 않는 빈 공간을 생략하는 기법들도 제안되었다. Wilhelms와 Gelder는[3] 각 정육면체 셀의 최소/최댓값을 옥트리(Octree) 형태로 미리 계산하여 처리해야 하는 셀의 개수를 줄이는 기 법을 제안하였다. Chen등은[4] 카티시안 격자를 블록 단위로 분할하여 각 블록의 최소/최댓값을 미리 계산하여 연산의 효 율성을 높이는 MC 기법을 제안하였다. 본 연구에서는 이러한 방법들을 응용하여 BCC 볼륨 데이터를 BCC 사면체 구조들 로 구성되는 블록으로 분할하여 빈 공간을 생략할 수 있도록 하였다.
3 배경지식
BCC 격자는 다양한 방법으로 정의할 수 있지만 가장 일반적인 방법은 카티시안 격자의 정육면체 셀의 중심에 격자점(Lattice point)을 추가하는 방법이다(그림 1a). 일반적으로 정수 좌표 를 얻기 위해 ℤBCC := 2ℤ3+{(0, 0, 0), (1, 1, 1)} 와 같이 정의한 다. (ℤ3 은 카티시안 격자를 뜻한다.) 본 연구에서는 이러한 정 의에 근거하여 4개의 정수로 BCC 격자점의 좌표를 지정한다. (0, 0, 0)(그림 1a의 검은색 점)과 (1, 1, 1)(그림 1a의적색점)은 각각 4 번째 좌표의 0과 1의 값을 갖는다. 예를 들어, BCC 격 자점 (13, 7, 11) = 2 · (6, 3, 5)+(1, 1, 1)은 (6, 3, 5, 1)의 좌표를 갖는다.
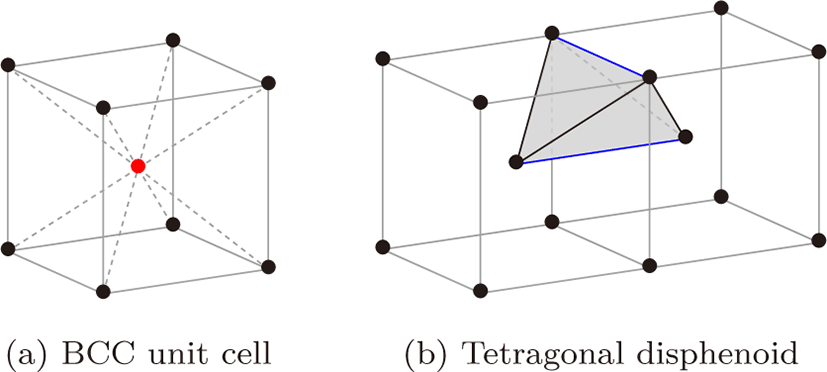
BCC 격자는 3차원 공간에서 가장 효율적인 샘플링 격자인 것 이 알려져 있고[1] tetragonal disphenoid라고 하는 고유의 사 면체 구조(그림 1b)를 포함하고 있다.[13] 이 구조는 그림 3과 같이 정사면체에 가까운 사면체의 복사본들로 공간을 채우는 패턴으로, 3차원 공간을 가장 균일하게 채울 수 있는 패턴 중의 하나로 알려져 있다.
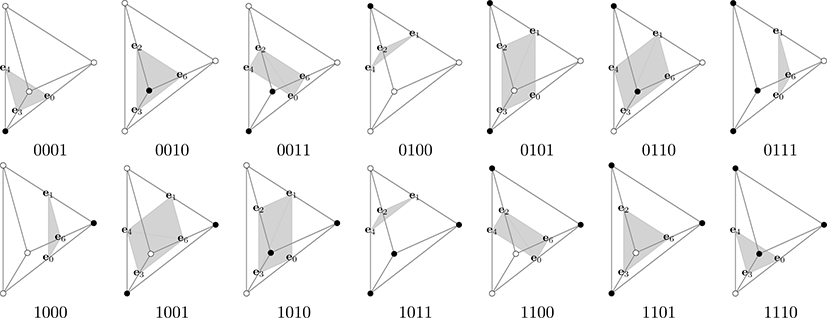
3차원 볼륨 데이터로부터 명시적인 등가면을 추출하는데 가장 널리 사용되는 MC 기법을 사면체 구조에 적용한 기법이 MT 기법이다. MT 기법은 MC 기법에 비해 더 많은 삼각형들로 이루어진 등가면을 생성한다는 단점은 있지만, MC 기법의 단점 중 하나인 모호성문제 (Ambiguity) 가 없고 참조테이블 (Lookup table) 의 크기가 훨씬 작다는 장점이 있다 (그림 4와 표 3).
마칭 기법은 기본적으로 각 셀에서의 등가면 추출이 독립적으 로 이루어지기 때문에 GPU에서 실행하기에 적합한 알고리즘 이다. 특히 MT 기법은 참조테이블의 크기가 매우 작아 GPU 의 메모리를 효율적으로 사용할 수 있도록 하기 때문에 GPU 구현에 더욱 적합한 알고리즘으로 알려져 있다.[10]
4 BCC 격자에서의 GPU MT 기법
본 연구에서 제안하는 BCC 격자에서의 GPU MT 기법은 다 음과 같은 다섯 단계로 이루어져 있다. 표 1은 전체 단계에서 사용하는 버퍼들의 목록이다.
-
블록 생성 단계: BCC 격자점들을 블록단위 그룹으로 모 으고각블록의최소/최대 데이터 값을 계산한다. 이 단계 는 처음 한 번만 수행한다.
-
유효 블록 추출 단계: 블록들 중 현재의 레벨값을 포함하 는 것들만을 추출한다.
-
표시 단계: 앞 단계에서 추출된 블록들에 포함된 엣지 및 사면체셀에대해등가면포함여부를엣지버퍼 (Edge buffer) 및셀버퍼(Cell buffer)에 각각 저장한다.
-
추출 단계 : 엣지 버퍼와 셀 버퍼에서 등가면을 포함하는 엣지와 셀을 따로 추출하여 각각 교차점 버퍼(Intersection buffer)와 삼각형 버퍼(Triangle buffer)에 저장한다.
-
메시 생성 단계: 교차점 버퍼의 각 엣지마다 교차점 좌표 및 법선 벡터를 계산하여 정점버퍼에 저장하고, 삼각형 버퍼의 각 삼각형에 대해 정점의 인덱스 정보를 읽어서 인덱스 버퍼를 만든다.
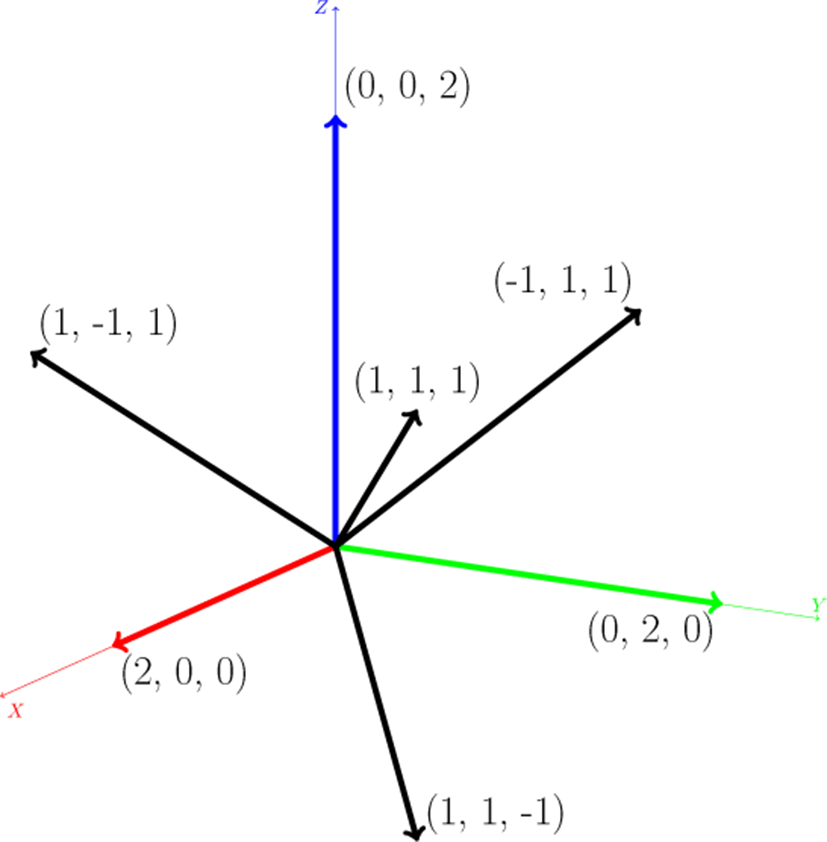
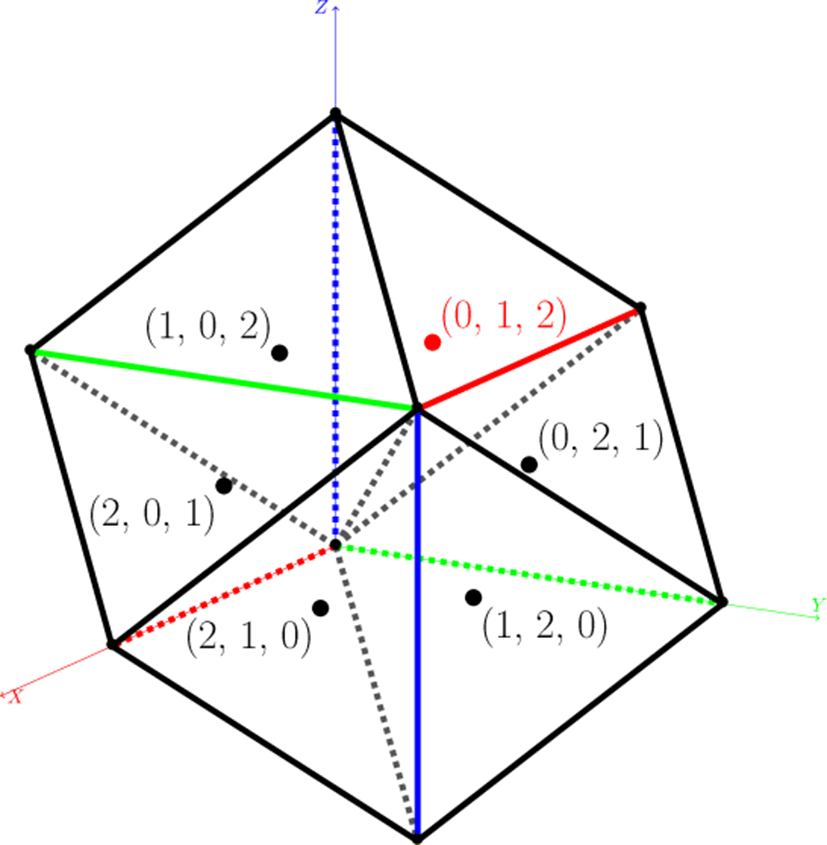
대부분의 경우 등가면이 생기는 엣지 및 셀의 비율은 50% 이하 정도로 매우 적다. 따라서 일정한 수의 셀들을 그룹 지어 (이를 “블록”이라 한다.) 각 블록의 최소/최댓값을 미리 계산한 후 렌더링 시에는 등가면을 포함하는 블록들만 처리하는 기법들 을 사용하였다. 본 연구에서는 그림 3와 같이 BCC 격자의 각 격자점(그림 3의 좌표원점)에 6개의 사면체 셀을 대응시켜 처 리하고 있다. 이러한 6개의 사면체는 8개의 격자점을 정점으 로 하는 육면체 (그림 3의 검은색 선으로 구성되는 육면체) 를 구성하게 된다. 이 구조를 반복하면 공간을 빈틈없이 채울 수 있고, 모든 BCC 격자점은 육면체의 정점 상에 위치하게 된다. 따라서 8개 격자점에서의 볼륨 데이터 값의 범위가 레벨값을 포함하지 않는다면 해당 셀들은 처리할 필요가 없게 된다.
이러한 과정을 GPU에서 효율적으로 처리하기 위해서는 적당 한 블록의 크기를 결정할 필요가 있다. GPU 연산은 일정한 단위의 쓰레드(Thread) 집합으로 이루어지는데, 이 단위는 제 조사마다 다소 차이가 있지만 대부분의 경우 32개(NVIDIA의 warp 등)또는 64개(AMD의 wavefront 등)로 정해진다. 그리 고 이 단위의 배수로 쓰레드 블록(Thread block)을 할당했을 때 가장 효율적인 연산이 가능하다. 본 연구에서는 4 × 4 × 4 × 2 = 128 개의 격자점에 대응되는 128개의 육면체 셀들을 하나의 격자점 블록으로 지정했다. 그리고 GPU 커널에서는 육면체 셀과 격자점 블록을 각각 GPU의 쓰레드와 쓰레드 블록에 할 당하고, 리덕션(Reduction)을 통해 격자점 블록의 최소/최댓 값을 계산한다. 계산된 최소/최댓값은 격자점 블록의 해상도 (Bx × By × Bz)와 동일한 크기의 3차원 배열에 따로 저장한다 (표 1의 blocks).
본 단계에서는 등가면을 포함하는 유효블록들을 추출하는 작 업을 수행한다. 각 쓰레드는 해당 블록이 등가면을 포함하는지 여부를 블록버퍼(표 1)에 저장한다. 다음으로는 직렬화 및 압 축을 적용하여 등가면을 포함하는 블록만을 추출한다(직렬화 및 압축은 4.4장에서 설명한다.).
| (a) | |
|---|---|
| Direction | Edge ID |
| (−1, 1, 1) | 0 |
| (1, −1, 1) | 1 |
| (1, 1, −1) | 2 |
| (1, 1, 1) | 3 |
| (0, 0, 2) | 4 |
| (0, 2, 0) | 5 |
| (2, 0, 0) | 6 |
| (b) | |
|---|---|
| Cell Type | Cell ID |
| (0,1,2) | 0 |
| (0,2,1) | 1 |
| (1,0,2) | 2 |
| (1,2,0) | 3 |
| (2,0,1) | 4 |
| (2,1,0) | 5 |
본 단계에서는 유효블록에 포함된 BCC 사면체 구조의 각 엣지 및 셀에 대해 등가면을 포함하는지 여부를 검사한 후 이를 각각 엣지 버퍼 및 셀 버퍼에 저장한다.
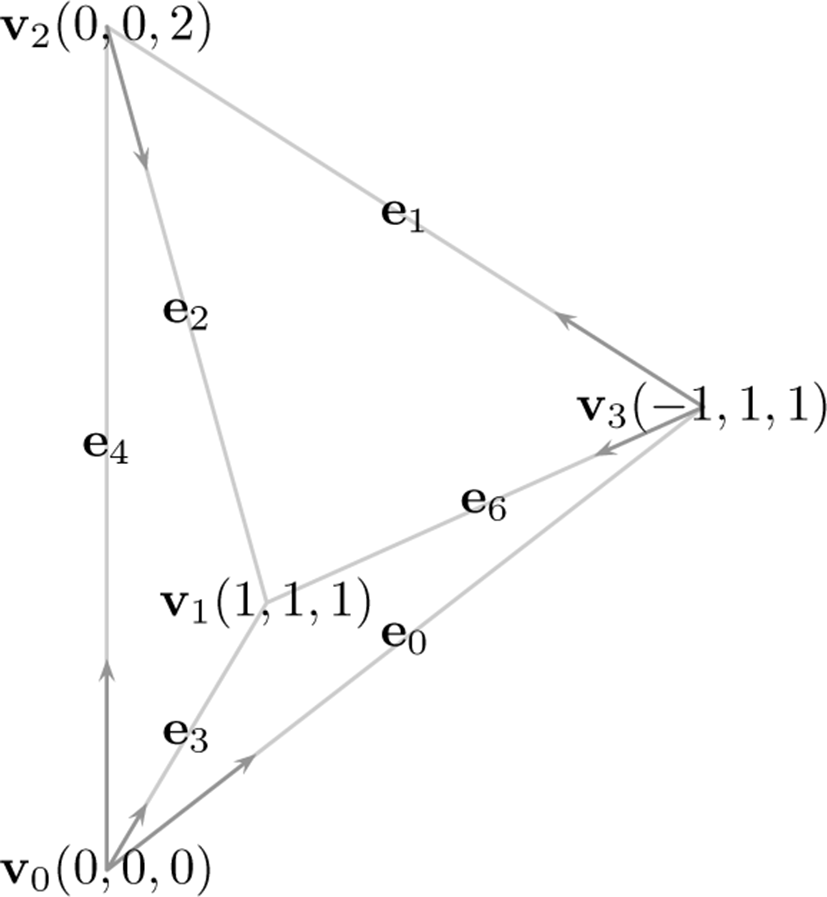
각 엣지의 등가면 포함 여부는 엣지의 두 정점 (격자점) 의데 이터 값을 레벨값(Isovalue)과 비교하여 알 수 있다. 이러한 연 산은 모든 엣지에서 독립적으로 이루어지기 때문에 엣지마다 쓰레드를 생성할 수도 있으나 이는 오히려 성능이 저하될 수 있다. 따라서 본 연구에서는 각 격자점마다 쓰레드를 생성한 후 해당 격자점에 연결된 전체 14개의 엣지들 중 7개의 엣지들에 대해 (그림 2, 표 2a) 중복없이 교차점검사를 수행한다. 각 엣지 는 4-튜플형식의격자점좌표와표 2a의 ID를 추가한 5-튜플로 표현할 수 있고, 이를 정수로 변환한 값을 인덱스로 사용하여 엣지 버퍼에 결과(등가면 생성여부, 0 또는 1)를 저장한다.
각 셀에 대한 등가면 검사는 사면체 셀의 4개의 정점에서의 볼륨 데이터 값을 레벨값과 비교하여 만들어진 4비트 키값을 사용하여 참조테이블(그림 4, 표 3)로부터 생성되는 삼각형의 개수(최대 2개)를 계산하여 이루어진다. 본 단계의 연산부하 대부분이 볼륨 데이터를 읽는 연산이기 때문에 재사용 비율을 최대한으로 높이고 쓰레드 생성으로 인한 부하를 줄이기 위해 앞에서 엣지 검사를 위해 생성한 격자점 쓰레드에서 셀 검사 작 업까지 모두 수행한다. 이를 위해 그림 3과 같이 각 격자점마다 6개의 사면체 셀을 중복없이 대응시켜 처리한다. 각 셀의 ID 는표 2b와 같이 부여하고 엣지와 마찬가지로 5-튜플을 정수로 변환한 값을 인덱스로 사용하여 셀인덱스 버퍼에는 삼각형의 개수를, 셀 버퍼에는 4 비트의 키값을 저장한다.
종합하면, 격자점에 대응되는 각 쓰레드에서 주변 8개 격자점 (그림 3의 8개의 사면체 정점들) 의볼륨 데이터값을읽은후 이를 이용해 7개의 엣지(그림 2) 및 6개의 셀(그림 3)의 등가면 포함 여부를 수행한다.
본 단계에서는 직렬화(Serialization) 및 압축(Compaction) 연 산을 통해 앞 단계에서 등가면을 포함한다고 표시된 엣지 및 셀을 추출하여 다음 단계에서 최소한의 쓰레드만을 생성하도 록 한다. 앞에서 설명한 “유효 블록 추출 단계”도 이와 비슷한 작업을 수행한다.
직렬화란, 등가면을 포함하는 엣지(셀)에 순차적으로 일련번 호를 부여하는 작업이다. 이 과정을 통해 등가면을 포함하는 엣지(셀)는 엣지인덱스 버퍼(셀인덱스 버퍼) 안에 각각 고유 한 인덱스값을 갖게 된다. (셀인덱스 버퍼의 경우 삼각형이 2 개 생기는 셀은 일련번호가 2 증가한다.) 참고로 엣지인덱스 버퍼는 마지막에 인덱스 버퍼를 생성할 때 정점의 인덱스를 얻기 위한 참조테이블의 역할을 수행한다.
압축 단계에서는 인덱스가 부여된 엣지와 셀만을 추출하여 각각 교차점 버퍼와 삼각형 버퍼로 옮기는 작업을 수행한다. 각 쓰레드는 엣지(셀)버퍼를 읽어 현재 처리하는 엣지(셀)가 등가면을 포함하는 경우 엣지인덱스 버퍼 (셀인덱스 버퍼) 에 서 인덱스값을 읽어 교차 점버퍼(삼각형 버퍼)의 해당 위치에 해당 엣지 (셀) 의 정수 좌표 (쓰레드 번호) 를 저장한다. 셀의 경우에는 키값도 함께 저장하는데, 셀에서 2개의 삼각형이 생 성되는 경우에는 삼각형 버퍼에 두 개의 값을 저장하고 이를 구별하기 위해 키값에 한 비트를 추가하여 5비트의 키값으로 저장한다. 한 개의 삼각형이 생성되는 경우에는 추가된 비트 값을 0으로 저장한다.
본 연구에서는 Parallel prefix sum 기법[14]을 응용하여 직렬 화와 압축 연산을 구현했다.
본 단계에서는 교차점 버퍼와 삼각형 버퍼의 각 요소에 대응하 는 쓰레드를 생성하여 정점 버퍼 및 인덱스 버퍼를 각각 생성 한다. 이전의 ”표시 단계”에서는 각 격자점에 연결된 엣지 및 셀들을 한 쓰레드에서 모두 처리했기 때문에 엣지 및 셀의 타입 (방향성)이 연산에 큰 영향을 미치지 않았다. (그림 3과 그림 2 참조) 하지만 본 단계에서는 각 쓰레드가 하나의 엣지 (셀) 를 처리하기 때문에, 처리하는 엣지(셀)이어떤종류인지를판단 하고 이에 따라 다른 작업을 수행해야 하는 문제가 있다.
우선 정점 버퍼 생성 과정을 살펴보자. 정점 버퍼 생성 쓰레 드는 교차점 버퍼에 대응되어 생성된다. 따라서 각 쓰레드는 자신이 처리해야 하는 엣지의 종류를 알아낼 필요가 있다. 앞 에서 정수로 변환한 인덱스를 다시 5-튜플로 변환한 후 마지막 좌표(0,...,6)를 키값으로 표 2a로부터 엣지의 방향을 알 수 있 다. 이때 현재의 격자점 좌표에 엣지 방향을 더하면 엣지의 반 대쪽 격자점 좌표를 얻을 수 있고 이를 통해 엣지 양 끝의 볼륨 데이터 값을 읽은 후 선형보간을 통해 교차점의 위치를 계산 하여 정점 버퍼에 저장한다. 사용하는 메모리를 최소한으로 줄이기 위해 정점버퍼는 따로 할당하지 않고 int3 타입의 교차 점 버퍼를 float3로 타입캐스팅(Type casting)하여 사용한다. 법선 벡터는 각 엣지의 양 끝 격자점에서의 기울기(Gradient) 를 유한차분법(Finite difference method)으로 구한 후 이를 선 형보간하여 계산한다.
다음으로는 인덱스 버퍼 생성과정을 살펴보자. 각 쓰레드는 우 선 삼각형 버퍼에 저장되어 있는 인덱스를 4-튜플로 변환하여 처리해야 하는 삼각형이 들어있는 셀의 정보를 얻는다. 생성 하는 삼각형 의 정점들은 셀의 6개의 엣지들로 이루어져 있다. 삼각형 버퍼에 저장되어 있는 5비트 키값을 이용하여 참조테 이블(표 3)로부터 정점을 이루는 엣지들의 상대적인 좌표들을 얻을 수 있다. 그런데 BCC 사면체구조는 모두 6종류의 셀들 을 포함하고 각 셀에 따라 참조테이블이 다르므로 이를 모두 포함 한다면 참조테이블의 크기가 너무 커지게 된다. 따라서 본 논문에서는 BCC 사면제구조의 규칙적인 패턴을 활용하여 그 중 그림 5의 기준사면체(Reference tetrahedron)에 대한 연 결구조만을 참조테이블 (표 3, 표 4) 로 저장하고 나머지 셀에 대해서는 이 테이블의 값을 변환하는 방식을 사용한다. 한 격 자점에 연결된 여섯 종류의 셀들은 그림 3에서 볼 수 있듯이 3 차원 순열(Permutation)의 변환관계를 갖는다. 따라서 표 4의 격자점 오프셋(Lattice offset)과 엣지 방향(Direction) 모두에 각 셀에 해당하는 순열변환을 적용하면 해당 셀의 격자점 오프 셋과 엣지 방향을 얻을 수 있다. 실제 GPU 구현에서는 참조테 이블은 상수 메모리 (Constant memory) 에 할당했고, 순열변 환은 OpenCL의 shuffle 함수를 사용했다.
| Edge | Lattice offset | Direction |
|---|---|---|
| e0 | ( 0,0,0) | (−1, 1, 1) |
| e1 | (−1,1,1) | ( 1,−1, 1) |
| e2 | ( 0,0,2) | ( 1, 1,−1) |
| e3 | ( 0,0,0) | ( 1, 1, 1) |
| e4 | ( 0,0,0) | ( 0, 0, 2) |
| e6 | (−1,1,1) | ( 2, 0, 0) |
5 실험 결과
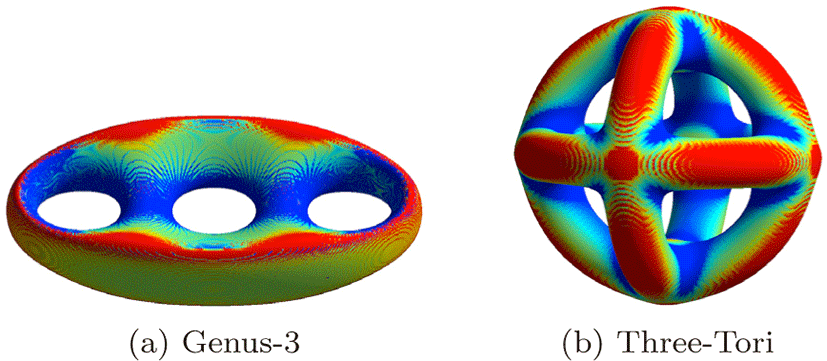
제안한 방법의 성능을 측정하기 위해 Genus-3 와 Three-Tori 두 음함수를 샘플링하여 다양한 크기의 볼륨 데이터를 생성 했다 (표 5, 그림 6). 성능 측정은 삼각형 집합 구조의 등가면 을 생성하는 고전적인 MT 기법을 구현하여 본 논문의 방법과 비교하였으며, 측정 항목은 해상도 증가에 따른 메모리 사용 량과 실행 시간이다. 측정에 사용한 장치는 Intel® Core™ i5-2500 CPU @ 3.30GHz CPU와 NVIDIA GeForce RTX 2080 Ti GPU 로 구성했다.
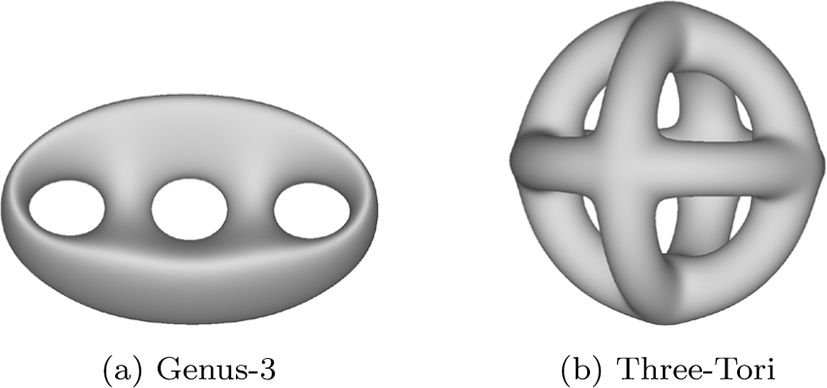
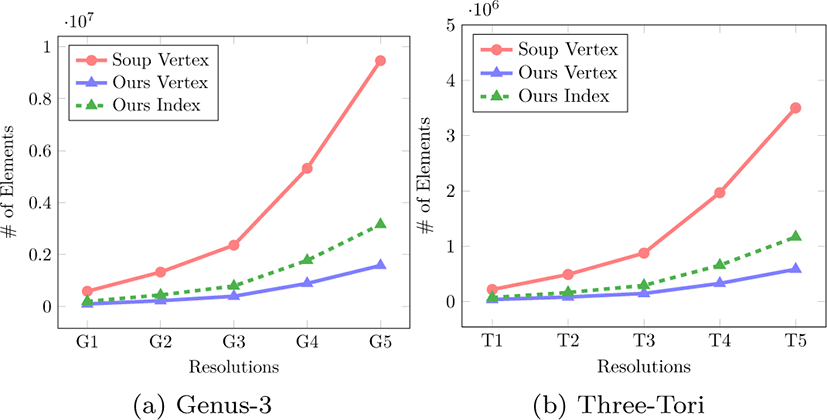
그림 6은 고해상도의 두 모델(표 5의 G5와 T5)에 대해서 등가 면을 추출한 결과이다. 본 방법은 삼각형 메시 형태의 데이터를 생성하기 때문에 고전적인 MT를 통해 얻은 방법과 동일한 형 태를 보이지만 등가면 데이터의 구조에서 차이점이 존재한다. 삼각형 메시 형태의 데이터는 삼각형 집합 형태와 완전히 동일 한 삼각형들을 표현면서도 중복되는 정점 데이터가 없는 장점 을 가지는 반면에 추가적인 인덱스 버퍼가 필요하다. 그림 7을 살펴보면 저해상도에서는 비슷한 크기의 결과를 생성하지만 (그림 7a의 G1과 그림 7b의 T1), 고해상도로 갈수록 삼각형 메 시 구조가 효율적으로 등가면을 표현함을 알 수 있다(그림 7a 의 G5와 그림 7b의 T5). 또한 메시 구조는 인덱스 버퍼를 통해 삼각형의 연결정보를 보다 쉽게 알 수 있기 때문에 추가적인 후처리 과정에서 더욱 효과적으로 사용될 수 있다.
추출되는 삼각형 메시는 등가면의 형태에 따라 크기가 유동 적이고, 사전에 정확한 크기를 측정하는 것이 어렵다. 게다가 시뮬레이션과 같이 반복적으로 등가면을 추출하는 경우에는 매 프레임마다 새로 메모리를 할당하는 것보다 사전에 충분히 큰 메모리 공간을 할당하는 것이 효율적이다. 또한 실시간 렌 더링에 응용하는 경우에는 미리 할당된 그래픽스 파이프라인 (Graphics pipeline) 의 버퍼와 연동해야 한다. 따라서 삼각형 메시를 저장하기 위한 충분히 큰 고정된 크기의 GPU 메모리가 미리 할당되어 있음을 가정하고, 이를 제외한 나머지 버퍼에 대한 메모리 사용량을 측정했다.
본 기법에서 사용하는 블록인덱스 버퍼, 엣지 버퍼, 셀 버퍼, 엣지인덱스 버퍼 그리고 셀인덱스 버퍼 (표 1) 는 볼륨 데이터 의 크기에 비례하여 커지지만 빈 공간 생략기법을 사용하여 사전에 버퍼의 크기를 제한 할 수 있다. 그림 8은본기법의각 버퍼의 크기를 50%로 제한하여 실험한 결과로 고전적인 MT 기법보다 다소 높은 메모리 사용량을 보다.

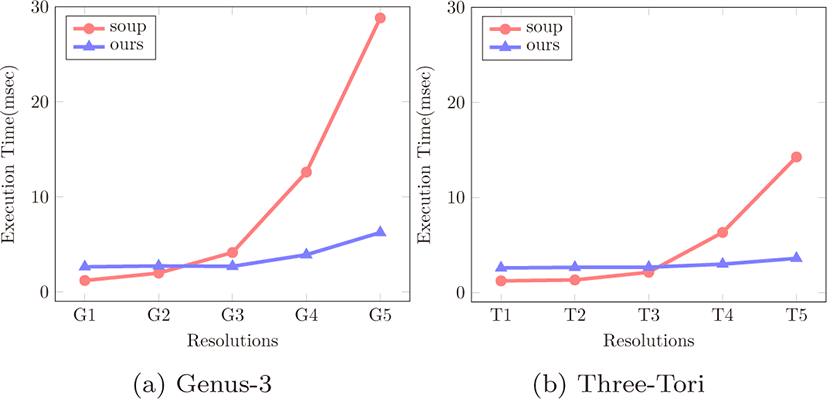
등가면 추출 시간은 볼륨 데이터 업로드 시간과 파일 출력을 제외한 등가면 추출에 걸린 시간만을 측정했다. 그림 9는각 모델의 해상도 변화에 따른 등가면 추출 시간이다. 저해상도 (그림 9a의 G1과 그림 9b의 T1과 T2)에서는 빈 공간이 생략되 는 비율이 적고 삼각형 메시 구조를 생성하기 위한 부가적인 연산들 때문에, 본 기법이 고전적인 방법보다 2배 이상 느린 결과를 보여준다. 하지만 고해상도로 갈수록 빈 공간의 비율이 높아지기 때문에 제안하는 방법이 고전적인 방법에 비해 매우 빠르게 등가면을 추출 할 수 있음을 보인다. 특히 그림 9a의 G5 와 그림 9b의 T5와 같은 매우 높은 해상도의 데이터에서 5배 에 가까운 등가면 추출 속도의 향상을 보인다. 또한 본 기법은 볼륨 데이터의 크기에 따른 등가면 추출시간의 증가폭이 크지 않은 장점을 가진다. 이를 통해 제안하는 방법이 고해상도의 데이터에서 보다 효율적인 등가면 추출이 가능함을 보여준다.
6 결론
본 논문이 제안하는 방법은 연결된 메시 형태의 등가면을 추출 하는 GPU 기반의 MT 기법이다. 메시구조는삼각형집합형 태의 구조보다 중복되는 정점이 없어서 데이터의 크기가 작고 인덱싱이 되어 있어 렌더링에 효율적이며 다양한 응용에 활용 할 수 있는 장점이 있다. 예를 들어 그림 10은 Griffin의 기법[2] 을 사용하여 본 논문의 방법을 곡률 렌더링에 활용한 결과이다. 이 기법 곡률을 계산하기 위해서 정점을 공유하는 삼각형 형태 의 중간 데이터를 생성하는데, 이러한 과정에서 삼각형 메시 형태는 계산상의 이점을 가진다.
본 논문의 방법은 기존의 마칭 기법에 비해 다소 복잡하고 더 많은 GPU 메모리가 필요하지만, 대다수의 볼륨 데이터에 존 재하는 많은 빈 공간을 생략하여 메모리 사용량을 크게 늘리지 않으면서도 빠르게 등가면을 추출할 수 있음을 보였다. 그리 고 이러한 장점은 고해상도의 데이터를 사용할 때 더욱 크게 나타남을 보였다. 하지만 빈 공간을 생략하는 기법은 기존의 삼각형 수프 기반의 마칭 기법들에도 쉽게 적용할 수 있기 때 문에 본 방법이 궁극적으로 더 좋은 성능을 보인다고 하기는 어렵다. 게다가 일부 볼륨 데이터들은 매우 많은 노이즈를 포 함하거나 등가면의 형태가 매우 복잡하여 빈 공간이 거의 없는 극단적인 경우도 존재하고 이러한 볼륨 데이터에는 빈 공간을 생략하여 성능을 높이는 것이 불가능하다. 이런 점들을 보완 하는 방법으로 슬라이딩 윈도(Sliding window) 방법을 생각해 볼 수 있다. 볼륨 데이터의 일부 슬라이스(Slice)들을 포함하는 격자 블록들의 집합을 생성하고 이러한 슬라이스를 이동하면 서 삼각형을 추출하면 더욱 낮은 메모리를 사용하면서도 빠른 등가면 추출이 가능할 것으로 예상한다.