정적 드레이프를 이용한 니트 옷감의 시뮬레이션 파라미터 추정

주, 은정; 최, 명걸

doi:10.15701/kcgs.2020.26.5.15

J Korea Comput Graph Soc 2020; 26(5):15-24

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2020.26.5.15

Article

정적 드레이프를 이용한 니트 옷감의 시뮬레이션 파라미터 추정

주은정¹

, 최명걸²^,^*

Estimating Simulation Parameters for Kint Fabrics from Static Drapes

Eunjung Ju¹

, Myung Geol Choi²^,^*

Author Information & Copyright ▼

¹(주)클로버추얼패션 kate@clo3d.com

²가톨릭대학교 mgchoi@catholic.ac.kr

¹CLO Virtual Fashion Inc.

²The Catholic University of Korea

^*Myung Geol Choi/The Catholic University of Korea(mgchoi@catholic.ac.kr)

© Copyright 2020 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Oct 05, 2020; Revised: Nov 13, 2020; Accepted: Nov 20, 2020

Published Online: Dec 31, 2020

요약

본 연구에서는 주어진 옷감 시료의 정적 드레이프 모양으로부터 해당 옷감을 시뮬레이션하기 위해필요한 시뮬레이션 파라미 터를 추정하는 데이터 기반 학습법을 제시한다. 정적 드레이프의 모양을 형성하기 위해 의류 산업계에서 옷감을 물성에 따라 분류하기 위해 사용하는 쿠식 드레이프 (Cusick’s drape)에서 착안한 방법을 사용한다. 학습 모델의입력 벡터는 특정 옷감의 정적 드레이프 모양에서 추출한 특징 벡터와옷감의 밀도 값으로 구성되고, 출력 벡터는 해당 드레이프 결과를 도출하는 여섯 가지 시뮬레이션 파라미터로 구성된다. 실제에 가깝고 편향되지 않은 학습 데이터를 생성하고자 먼저 400가지의 실제 니트 옷감에 대한 시뮬레이션 파라미터를 수집하고 이로부터 GMM (Gaussian mixture model) 생성 모델을 만든다. 다음, GMM 확률분포에 따라 대량의 시뮬레이션 파라미터를 무작위 샘플링한다. 샘플링된 각각의 시뮬레이션 파라미터에 대해 옷감 시 뮬레이션을 수행하여 가상의 정적 드레이프 결과를 만들고 이로부터 특징 벡터를 추출한다. 생성된 데이터를 로그선형회기 (log-linear regression) 모델로 피팅한다. 학습의 수치적 정확도를 검증하고 시뮬레이션 결과의 시각적 유사도를 비교하여 제시된 방법의유용성을 확인한다.

Abstract

We present a supervised learning method that estimates the simulation parameters required to simulate the fabric from the static drape shape of a given fabric sample. The static drape shape was inspired by Cusick’s drape, which is used in the apparel industry to classify fabrics according to their mechanical properties. The input vector of the training model consists of the feature vector extracted from the static drape and the density value of a fabric specimen. The output vector consists of six simulation parameters that have a signiﬁcant inﬂuence on deriving the corresponding drape result. To generate a plausible and unbiased training data set, we ﬁrst collect simulation parameters for 400 knit fabrics and generate a Gaussian Mixed Model (GMM) generation model from them. Next, a large number of simulation parameters are randomly sampled from the GMM model, and cloth simulation is performed for each sampled simulation parameter to create a virtual static drape. The generated training data is ﬁtted with a log-linear regression model. To evaluate our method, we check the accuracy of the training results with a test data set and compare the visual similarity of the simulated drapes.

Keywords: 옷감; 시뮬레이션; 파라미터 추정; 정적 드레이프; 회기

Keywords: Cloth; Simulation; Parameter Estimation; Static Drape; Regression

1. 서론

옷감 시뮬레이션 기술은 패션섬유 산업 분야에서 널리 사용되고 있다. 대표적인 예로 새로운 의상 디자인을 개발하는 과정에서 가상 시뮬레이션을 통해 최종 결과를 예측하고 문제를 보완하 는 방법으로 개발 비용을 줄이고 완성도를 높인다. 시뮬레이터 사용자는 특정한 옷감의 성질을 가상으로 표현하기 위해서 해당 옷감에 대한 시뮬레이션 파라미터를 설정해야 한다. 일반적으로 시뮬레이션 파라미터는 실제 옷감에 대한 여러 가지 물리적 특성 값에 대응된다. 즉, 사용자는 표현하고자 하는 옷감의 밀도, 신축 강도, 굽힘 강도 등을 측정하여 시뮬레이션 파라미터로 입력해야 한다.

하지만 이러한 방법에는 두 가지 어려움이 있다. 첫째는 신축 강도, 굽힘 강도 등의 물성을 정확히 측정하기 위해서는 고가의 장비가 필요하다는 점이다. 일반 사용자나 개인 디자이너는 이러 한 장비에 접근이 쉽지 않다. 둘째는 실제 옷감의 물리적 메커니 즘과 시뮬레이터의 메커니즘에는 차이기 있으므로 정확한 물성 값을입력한다고 하여도 원하는 옷감의 성질을 표현하지 못하는 경우가 많다는 것이다. 일반 사용자가 본인이 입력한 시뮬레이션 파라미터가 목표 옷감의 물성을 충분히 유사하게 표현하고 있는 지 확인하는 방법 중 하나는 쿠식 드레이프 테스트 [1]와 같은 간단한 방법으로 드레이프 모양을 확인하는 것이다. 실제 옷감 의 드레이프와 시뮬레이션 결과의 드레이프가 유사하다면 현재 시뮬레이션 파라미터에 대한 정확도가 확인된다. 하지만 두드레 이프 모양이 서로 다르다면 일반 사용자로서는 현재 파라미터에 대한 정확도를 신뢰하기 어렵다. 이 경우 일정 범위 내에서 파라 미터를 조정하며 시뮬레이션을 반복하는 파라미터 튜닝 과정이 필요하다. 하지만 옷감 시뮬레이터는 메커니즘 복잡하여 수동 파 라미터 튜닝이 매우 어려운 것으로 알려져 있다. 자동으로 목표로 하는 드레이프 모양을 얻을 때까지 시뮬레이션을 반복하는 최적 화 기법 [2, 3, 4, 5, 6]이 제시되기도 하였으나 하나의 옷감에 대한 파라미터를 추정하기 위해 수십 시간의 계산 시간이 필요하므로 여러 번 옷감의 종류를 바꾸어 가며 결과를 확인하고 싶어 하는 사용자 입장에서는 실용성이 떨어진다.

본 연구에서는 학습을 통해 니트 옷감의 정적 드레이프 모양으 로부로 해당 옷감의 시뮬레이션 파라미터를 추정하는 실용적인 방법을 제시한다. 정적 드레이프 모양을 형성하기 위해 쿠식 드 레이프 테스트에서 착안한 간단한 방법을 사용한다. 쿠식 드레이 프는 의류 산업계에서 옷감을 물성에 따라 분류하는 용도로 주로 사용되어왔으며, 옷감의 여러 물성 수치와 밀접한 상관관계가 있 음이 알려져 있다 [7, 8, 9, 10].

제시하는 방법은 정사각형 시료를 원기둥 위에 올려놓았을 때 형성되는 드레이프 모양을 사용하는 것이다. 본 연구에서 추정 대 상으로 하는 시뮬레이션 파라미터는 정적 드레이프 모양 형성에 큰 영향을 미치는 여섯 가지이며, 구체적으로 위사, 경사, 대각선 방향에 대한 신축성 강도 (stretch stiffness)와 굽힘 강도 (bending stiffness)이다. 시뮬레이터는 실제 패션 디자인 산업체에서 널리 사용되고 있는 CLO3D 시뮬레이터를 사용한다.

학습 데이터는 시뮬레이션을 통해 대량 생산한다. 먼저 시뮬 레이션 파라미터 데이터를 대량으로 생성하기 위해 400가지의 실제 니트 옷감에 대한 시뮬레이션 파라미터를 획득하였고, 이로 부터 GMM (Gaussian mixture model) 생성 모델을 만들고 확률 분포에 따라 무작위 샘플링한다. 다음, 샘플링된 각각의 파라미 터 집합에 대해 옷감 시뮬레이션을 수행하여 드레이프 데이터를 수집한다. 가상 드레이프 결과는 3차원 모델로 저장되지만 학습 에서는 3차원 모델 전체를 사용하는 대신 테두리를 따라 형성되 는 3차원 곡선과 실제 옷감의 밀도를 특징 벡터로 사용한다. 학습 모델은 로그선형회기 (log-linear regression 또는 LLR) 모델을 사 용한다.

기존 연구에 의하면 옷감의 물리적 특성값에 대한 로그 값의 변화는 드레이프 모양 변화와 대체로 선형 관계에 있다고 알려 져 있다 [7, 11, 12]. 본 연구에서 제시된 특징 벡터의 변화 역시 시뮬레이션 파라미터 변화에 대한 로그 값의 변화와 대체로 선형 관계에 있음을 증명하여 타당성을 확인한다. 또한, 학습에 사용 되지 않은 데이터를 테스트 데이터로 사용하여 학습 정확도를 측정하고 유용성을 검증한다.

2. 연구 배경

옷감 물성을 직접 측정하는 대표적인 방법은 가와바타 측정법 (Kawabata estimating system 또는 KES) [13]을 사용하는 것이다. KES는 시료의 마찰력, 질량 등의 단순한 물성 뿐만 아니라 인장 강도 (tensile stiffness), 굽힘 강도 (bending stiffness), 전단 강도 (shear stiffness) 등의 기계적 물성 (mechanical property)까지 정 밀하게 측정하는 기계 장치이다. 이러한 물성 값의 상당 부분은 일반적인 옷감 시뮬레이터에서 시뮬레이션 파라미터로 정의되 는 물성과 일치한다. Breen 등은 KES 측정값을 직접 시뮬레이션 파라미터로 사용하였다 [14]. 하지만 가상 시뮬레이터의 메커니 즘은 현실에서의 옷감 메커니즘과 차이가 있으므로 실제 옷감의 정밀한 물성값을 사용했을 때 의도한 결과를 얻지 못하는 경우 가 많다. 반면, 본 연구의 목표는 옷감의 실제 물성을 측정하는 것이 아니라 원하는 정적 드레이프 모양을 생성하는 시뮬레이션 파라미터를 추정하는 것이다.

2.1 펄럭임 드레이프 vs. 쿠식 드레이프

옷감의 드레이프 모양과 물성 사이의 관계에 관한 연구는 의류학 분야와 컴퓨터 그래픽스 분야에서 활발히 연구되어 오고 있다. 컴퓨터 그래픽스 분야에서는 사각형 모양의 옷감 시료를 공중에 걸고 인공 바람을 이용해 시료가 펄럭이도록 하는 동적 드레이 프를 주로 사용해왔다 (그림 1(a) 참조). 본 논문에서는 이러한 방식을 편의상 “펄럭임 드레이프”라 부른다. 기존 연구에서는 주 로 특정 옷감에 대한 펄럭임 드레이프를 비디오로 촬영하고 이를 보고 굽힘 강도나 무게 등의 시뮬레이션 파라미터를 유추하였 다 [2, 11, 15, 16, 12]. 펄럭임 드레이프의 장점은 굽힘 강도 등의 일부 물성에 대해서는 사람이 보아도 어느 정도 물성 수치를 파 악할 수 있을 만큼 시각적으로 뚜렷한 변화를 보인다는 것이다. 하지만 비디오가 아닌 정지 장면에서는 사람의육안이든 기계적 학습이든 물성을 파악하기 어렵다는 단점이있다 [11, 12].

Figure 1: Comparison between waving drape, Cusick’s drape and our square drape.

Download Original Figure

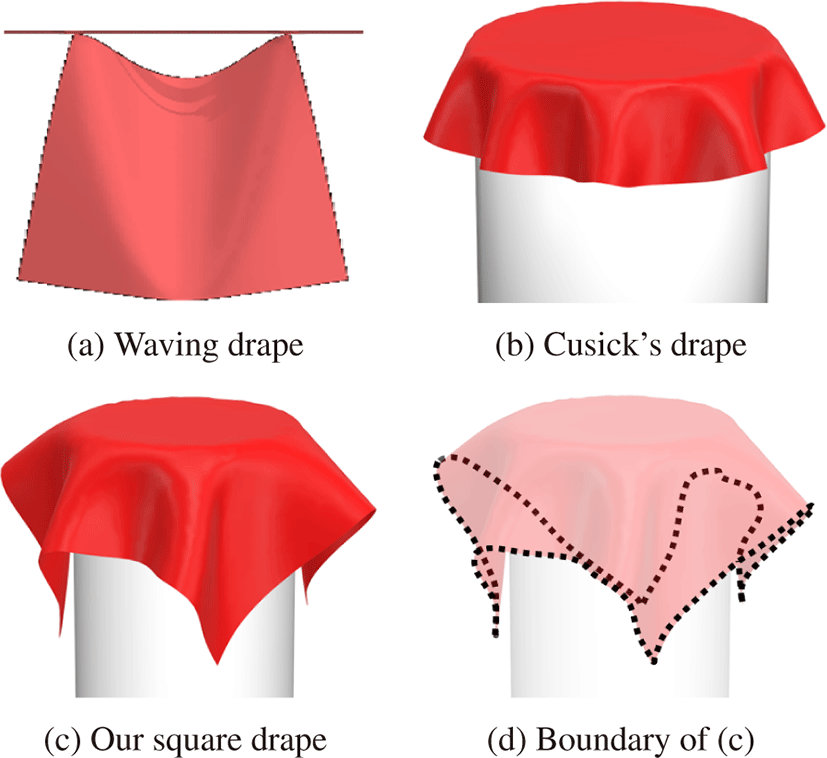
한편, 의류 산업 분야에서는 “쿠식 드레이프” [1], 또는 그에 서 파생된 드레이프 방법을 주로 사용하였다 (그림 1(b) 참조). 쿠식 드레이프란 원형의 옷감 시료를 그보다 반지름이 작은 원 판 위에 올려놓고가장자리 부분이 흘러내려 주름이 형성되도록 하는 방법이다. 쿠식 드레이프는 대체로 탑다운 방향에서 2차원 이미지로 투영한 후 분석된다. 쿠식 드레이프 테스트를 이용한 다양한 분석 법에 대해서는 Carrera-Gallissà 등이 발표한 논문을 참조하기 추천한다 [17]. 쿠식 드레이프는 KES로 측정되는 대부 분의 수치와 밀접한 상관관계가 있음이 여러 실험을 통해 증명되 었다 [7, 8, 9, 10]. 예를 들어 Lam 등은 인공신경망 학습을 이용 하여 옷감의 물성으로부터 쿠식 드레이프 계수를 추정하는 기술 을 제시하였다 [18]. 또한, 쿠식 드레이프 기법은 동적 드레이프 측정이나 3차원 드레이프 형상 분석을 위한 장치로 발전해가고 있다 [19, 20, 21, 22]. 본 연구에서는 쿠식 방법에서 착안한 정적 드레이프의 3차원 정보를 통해 시뮬레이션 파라미터를 추정하는 기술을 제시한다.

2.2 최적화 vs. 지도 학습

옷감 시료로부터 물성이나 시뮬레이션 파라미터를 추정하는 문 제는 크게 두 가지 접근 방법으로 연구되었다. 첫 번째는 최적화 접근법으로 목표로 하는 시뮬레이션 결과를 얻을 때까지 파라 미터를 조정하며 시뮬레이션을 반복하는 것이다. Bhat 등 [2]은 재현하고자 하는 옷감에 대한 펄럭임 드레이프 영상을 대상으로 이와 동일한 시뮬레이션 결과가 도출되도록 최적화하였다. Wang 등 [3]과 Miguel 등 [4]은 옷감 시료에 일정한 힘을 가하여 변형된 모양을 촬영하고 이와 같은 시뮬레이션 결과가 도출되도록 최적 화하였다. Mongus 등 [5]은 쿠식 드레이프 결과에서 얻은 특징 벡 터와 동일한 결과를 얻도록 최적화하였다. Yang 등 [6]은 사람이 옷을입고 찍은 사진에서의 드레이프 모양을 목표로 최적화하였 다. 이러한 최적화 기법들은 데이터 기반 학습법과 달리 별도의 학습 데이터가 필요 없다는 장점이 있다. 하지만 최적화 시간이 오래 걸리는 단점이 있어, 가상 환경에 여러가지 서로 다른 옷감 을 적용해보며 적절한 의상 디자인을 찾는 작업 방식에서는 실 용성이 떨어진다. 위에서 언급된 방법들은 하나의 옷감에 대한 시뮬레이션 파라미터를 최적화하기 위해 적게는 수시간 많게는 50시간 정도의 계산 시간이 필요하다.

두 번째 접근 방법은 사전에 준비된 학습 데이터로부터 지도 학 습 (supervised learning)하는 것이다. 기존 연구는 대부분 펄럭임 드레이프 영상을 학습 데이터로 사용하였다. Bouman 등 [11]과 Bi 등 [12]은 펄럭임 드레이프 영상으로부터 굽힘 강도와 무게를 학습하기 위해 수십 가지 실제 옷감 데이터를 사용하였다. 이들 연구의 목적은 실제 옷감의 물성을 추정하기 위한 것이었기 때문 에 추정된 값이 시뮬레이션 파라미터로 사용되었을 때의 효과는 확인하지 않았다. Yang 등 [16]은 시뮬레이션 파라미터 추정을 위한학습 기술을 제시하였다. 학습 데이터는 시뮬레이션 생성한 펄럭임 드레이프 영상을 사용하였다. 시뮬레이션 파라미터 수치 를 직접 추정하는 대신 54가지 옷감 타입을 지정한 후 그중 한 가지로 분류 (classiﬁction) 하는 방법으로 문제를 단순화하였다.

본 연구에서도 Yang 등 [16]의 방식과 유사하게 시뮬레이션을 통해 대량의 학습 데이터를 생성하고 이로부터 시뮬레이션 파라 미터를 추정하는 학습 모델을 제시한다. 하지만 펄럭임 드레이프 영상 대신 쿠식 드레이프에서 착안한 정적 드레이프를 사용하며, 옷감을 타입별로 분류하는 것이 아니라 시뮬레이션 파라미터 자 체를 추정한다. 일반 사용자 관점에서 정적 드레이프를 만드는 과정은 바람을 일으켜 펄럭임 드레이프를만드는 과정에 비하면 상당히 쉽다. 또한, 대량의 학습 데이터 생성에도 유리하여 실용 성이 높다.

3. 옷감 시뮬레이션 모델

본 실험에서는 의류 산업체에서 널리 사용되고 있는 CLO3D 시 뮬레이션 모델을 사용한다 [23]. 이 모델은 Baraff와 Witkin가 제 시한 시뮬레이션 모델에 기초하여 일부 기능을 최적화한 것이다. 시뮬레이션 모델에 대한 세부 사항은 Baraff와 Witkin의 논문 [24] 을 참조하기를 추천한다.

CLO3D에 정의된 시뮬레이션 파라미터 중 정적 드레이프 결과 에 가장 큰 영향을 미치는 6개를 학습 대상으로 선택하였다.6개 의 시뮬레이션 파라미터는 표 1와 같다. 이 파라미터들은 Baraff 와 Witkin의 옷감 모델에서 정의된 세 가진 기본 힘 (stretch force, shear force, bending force)에 연관된 파라미터들이다. 전체 실험 에서 나머지 시뮬레이션 파라미터의 값은 모두 CLO3D 소프트 웨어에서 정의한 기본값을 사용하였다.

Table 1: Target simulation parameters.

Symbol	Details of Parameter
SuK	Weft Stretch Stiffness (위사 신축성 강도 )
SvK	Warp Stretch Stiffness (경사신축성강도)
HK	Shear Stiffness (전단 강도)
BuK	Weft Bending Stiffness (위사 굽힘 강도)
BvK	Warp Bending Stiffness (경사 굽힘 강도)
BhK	Bias Bending Stiffness (대각 굽힘 강도)

Download Excel Table

4. 정적 드레이프와 특징 벡터

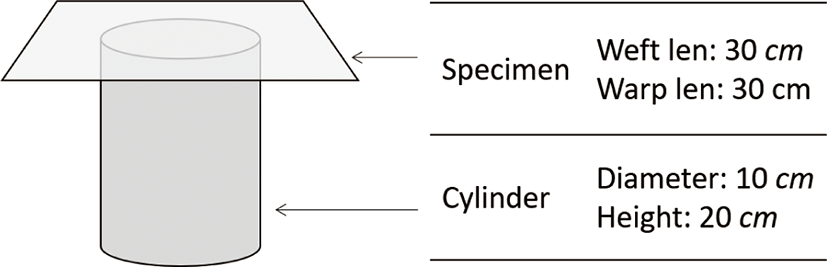
본 연구에서 제안하는 드레이프 형성 방법은 원기둥의 윗면에 원기둥 반지름보다 넓은 정사각형 옷감 시료를 펼쳐 올려놓는 것 이다. 앞으로 본 논문에서는 이러한 방법을 “정사각 드레이프” 라 부른다. 드레이프 모양에 대한 테두리 곡선과 옷감의 밀도를 입력 벡터로 사용한다. 다음의 세부 절에서 자세히 설명한다.

4.1 정사각 드레이프

일반적인 쿠식 드레이프는 반지름이 15cm인 원형으로 잘라낸 옷 감 시료를 반지름이 9cm인 원판 받침 위에 올려 놓고 드레이프를 형성하는 것이다. 이 경우옷감 시료에서 아래로 흘러내리는 영역 의 넓이가 본 연구에서 제시하는 드레이프에 비하여 좁다. 쿠식 드레이프는 주로 탑다운 방향에서 2차원 평면으로 투영하여 관 찰한다. 따라서 시료가 아래로 흘러내리는 부분이 넓을수록 시료 의 테두리 부분을 관찰할 수 없을 가능성이 커진다. 이를 피하기 위해 시료의 크기가 너무 넓지 않게 유지할필요가 있었다.

하지만 본 연구에서는 드레이프를 2차원으로 투영해서 관찰하 지 않고 3차원 형태를 유지한 채로 특징 벡터를 추출하므로 시료 가 흘러내리는 부분의 넓이를 제한할 필요가 없다. 본 연구에서 제시하는 방법은 30cm × 30cm 크기의 정사각형형태의 옷감 시 료를 사용한다. 정사각형의 평행한 두 변이 직물의 경사 방향과 일치하고 나머지 두 변은 직물의 위사 방향과 일치하도록 자른 다. 받침대는 반지름이 10cm이고 높이가 20cm인 원기둥을 사용 한다. 그림 2는 정사각 드레이프 실험의 초기 상태를 나타낸다. 정사각형 형태의 시료의 장점은 첫째, 위사 방향과 경사 방향의 구분이 쉽다는 것이다. 본 연구에서는 위사 방향과 경사 방향을 구분하여 신축성 강도와 굽힘 강도 파라미터를 추정하므로 방향 이 정확히 구분되는 것이 매우 중요하다. 둘째, 시료 자체 무게로 인한 드레이프 모양 변화도 보다 분명해진다. 그림 1(b)와 (c)는 같은 시뮬레이션 파라미터를 사용하여 쿠식 드레이프와 정사각 드레이프를 시뮬레이션한 결과를 나타낸다. 정사각 드레이프에 서 옷감 시료의 모서리 부분이 길게 흘러내려오는 것을 확인할 수 있다. 예를 들어 옷감 시료의 밀도가 높고강도가 낮을수록 이 부 분의 길이가 다른 부분에 비하여 상대적으로 길어지거나 아래로 더 가파르게 처질 것이다.

Figure 2: Initial state of our square drape simulation.

Download Original Figure

4.2 테두리 벡터

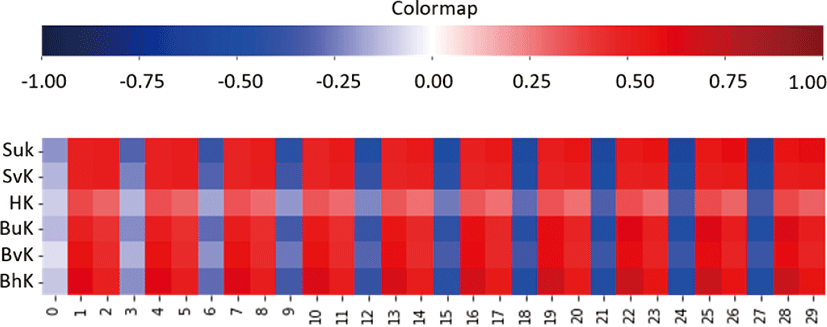
정사각 드레이프 결과에서 옷감 시료의 테두리를 따라 샘플링한 3차원 점의 집합을 특징 벡터로 사용한다 (그림 1(d) 참조). 본 연 구에서는 5mm 간격으로 균일하게 샘플링하여 3차원 점 244개에 대한 벡터로 표현한다. 테두리 벡터의 총 크기는 732 (= 244 × 3) 가 된다. 드레이프 전체 모양과 테두리 모양 사이에 1 대 1의 상관 관계가 있다고 가정하였다. 드레이프 전체 모양 대신 테두리 부 분만 샘플링하여 사용하면 학습 데이터의 복잡도를 크게 줄일 수 있다. 테두리 벡터로 시뮬레이션 파라미터를 학습하는 것이유효 한지 검증하기 위하여 테두리 벡터와 시뮬레이션 파라미터 사이 의 상관관계 행렬 (correlation matrix)을 계산해 보았다. 그림 3는 5.1 절에서설명하게 될 400개의 실제 니트 옷감을 대상으로 측정 한 시뮬레이션 파라미터 값과 그 값으로부터 정사각 드레이프를 시뮬레이션 하여얻은 테두리 벡터 사이의 상관관계 행렬의일부 를 시각화한 것이다. 수평축에 0에서 29까지 숫자는 전체 테두리 벡터 중 앞부분 30개에 해당하는 인덱스를 의미한다. 나머지 부 분에서도 비슷한 수준의 상관관계 수치가 나타난다. 전체적으로 상관관계 수치가 높은 것으로 확인된다.

Figure 3: Correlation matrix between the simulation parameters and the boundary vectors.

Download Original Figure

드레이프의 테두리를 샘플링 하기 위해 여러 가지 방법을 사용 할 수 있다. 학습 데이터의 경우에는 시뮬레이션으로 생성하므로 최종 드레이프의 3차원 메시 정보를 얻게 된다. 따라서 메시 모델 의 테두리를 쉽게 샘플링할 수 있다. 실제 옷감 시료의 경우에는 사진을 찍은 후에 3차원으로 복원하는 방법이나 3차원 스캐너를 사용하는 방법 등을 사용할 수 있다.

4.3 밀도

대부분의 옷감 시뮬레이션 모델에서는 옷감의 밀도를 시뮬레이 션 파라미터 중 하나로 사용한다. 옷감의 밀도는 중력에 따른 옷 감 형태 변화에 큰 영향을 미치기 때문이다. 본 연구에서 밀도는 추정 대상이 아니라 학습 모델의 입력값으로 사용한다. 밀도는 질량을 면적으로 나누어 쉽게 얻을 수 있는 물성값이므로 시료만 있다면 쉽게 측정 가능한다. 밀도를 고정된 입력값으로 사용했을 때의장점은 파라미터 추정에 대한 모호성이 현저히 낮아진다는 것이다. 예를 들어 드레이프 모양이 상대적으로 아래로 많이 처져 있는 경우 그 원인은 신축성 강도가 낮아서 일 수도 있지만, 밀도 가 높기 때문일 수도 있다. 밀도가 입력값으로 사용되면 이러한 모호함이 제거된다. 최종적으로 학습 모델의입력 벡터는 테두리 벡터에 밀도 값을 추가한 것으로 총 크기가 733이 된다.

5. 학습 데이터 생성과 학습 모델

이번 절에서는 대량의 학습 데이터 생성을위해 시뮬레이션 파라 미터를 수집하는 과정과 학습 모델에 대해 구체적으로 설명한다.

5.1 실제 옷감에 대한 시뮬레이션 파라미터

시뮬레이션 파라미터에 대한 무작위 샘플링에서 고려해야 하는 점은 물리적으로 비정상적인 조합이 샘플 되었을 때 옷감 시뮬레 이션의 결과가 비현실적이거나 발산할 수 있다는 것이다. 또한, 물리적으로 가능하나 옷감으로는 볼 수 없는 파라미터가 샘플링 되는 것도 가능한 피해야 한다. 이러한 노이즈 데이터가 많아지면 학습의 정확도가 낮아진다. 노이즈 데이터를 피하고자 먼저 실제 옷감에서 얻은 파라미터 데이터의 분포에 기초하여 생성 모델 (generative model)을 만들고 이로부터 대량의 데이터를 샘플링 한다.

본 연구를 위해 (주)클로버추얼패션에서 400개의 실제 옷감으 로부터 측정된 시뮬레이션 파라미터를 제공받았다. 400개 옷감 은 모두 니트 구조 옷감이며면, 린넨, 울, 폴리에스테르 나일론 등 다양한 소재의 천연섬유, 합성섬유, 혼합섬유가 포함되어 있다. 시뮬레이션 파라미터는 ’CLO Fabric Kit’ [25] 장치를 사용하여 각 옷감의 여러 가지 물성을 측정한 후 CLO3D 시뮬레이터에서 사용 가능한 형태로 변환한 것이다. 이렇게 얻은 시뮬레이션 파라 미터를 사용하여 정사각 드레이프를 시뮬레이션한 결과는 실제 옷감의 드레이프 모양과 서로 다르다. 시뮬레이터 고유의 메커니 즘 특성이 충분히 고려되지 않고 실제 물리적 특성값에 기초하여 만들어진 파라미터이기 때문이다. 하지만 이렇게 얻은 데이터가 실제 옷감들에 대한 시뮬레이션 파라미터의 분포와 세부 파라미 터 사이의 상관관계에 대한 정보를 포함하고 있다고 가정할 수 있다.

Table 2는 400개의 데이터에 대한 각 시뮬레이션 파라미터의 평균과 분산을 나타낸다. 분산의 크기로 보았을 때 서로 다른 물 성을 가진 다양한 옷감을 포함하고 있다고 볼 수 있다.

Table 2: The statistics of six parameters and density measured from the 400 real knit fabrics.

Parameter (unit)	Mean	Std. Dev.
SuK (g·mm²)	131010.96	158742.72
SvK (g·mm²)	163944.78	166105.29
HK (g·mm²)	75064.22	120353.45
BuK (g·mm²/s²/rad)	1119.74	3009.62
BvK (g·mm²/s²/rad)	1370.87	3244.53
BhK (g·mm²/s²/rad)	1245.30	2712.10
Density (g/mm²)	214.02	66.44

Download Excel Table

5.2 GMM 모델을이용한 데이터 생성

400개의 실제 옷감에 대한 7차원 시뮬레이션 파라미터 (6개의 최적화 대상 파라미터와 밀도) 데이터로부터 가우스혼합모델 (Gaussian mixture model, GMM)을 생성한다. GMM 모델의 클러 스터 수는 AIC (Akaike Information Criteiron) [26] 수치 검사로 결정한다. 본 실험에서 클러스터 수는 5로 정하였다. GMM 모델 을이용하여 원하는 만큼의 시뮬레이션 파라미터를 무작위로 생 성할 수 있다. GMM 모델을 사용하였을 때 장점은 클러스터별로 같은 수로 샘플링하는 방법으로 데이터 편중 문제를 피할 수 있 다는 것이다. 샘플링된 각 파라미터에 대응하는 정사각 드레이프 데이터는 시뮬레이션으로 생성한다.

생성된 전체 데이터 집합 D는 아래와 같이 정의된다.

D = {(p 0, q 0), (p 1, q 1), …, (p n, q n)}, p i ∈ ℝ 733, q i ∈ ℝ 6

학습에서 입력 벡터로 사용될 벡터 p_i는 정사각 드레이프 시뮬 레이션 결과에서 추출한 테두리 벡터와 밀도 값으로 이루진 733 차원 벡터이고, 학습에서 출력 벡터로 사용될 벡터 q_i는 최적화 대상인 6개의 시뮬레이션 파라미터에 대한 벡터이다.

5.3 로그선형회기 학습 모델

Hu 등 [7]의 연구에 의하면 쿠식 드레이프 계수와옷감의 물성 수 치의 상관관계보다 물성 수치에 로그를 취한 값과의 상관관계가 더 높게 나타났다. Bouman 등 [11]과 Bi 등 [12]의 연구에 의하 면 사람이 시각적으로 느끼는 드레이프 모양 변화의 크기는 실제 옷감의 굽힘 강도 변화의 로그 값에 대체로 비례하는 것으로 나타 났다. 이러한 사실에 기초하여 로그선형회기 모델을 적용하였다.

먼저전체 학습 데이터를 다음과같은 방법으로 정규화한다.

p i ′ = norm (p i) q i ′ = norm (log (q i))

학습 데이터의입력값인 p_i는 전체 데이터의 최댓값과 최솟값을 이용하여 요소별로 0에서 1 사이 범위로 정규화한다. 학습 데이터 의 출력값인 q_i는 먼저 모든 요소에 자연로그를 취한 후 최댓값과 최솟값을 이용하여 0에서 1 사이 범위로 정규화한다. 출력 데이 터에 미리 로그를 취하였으므로 학습 모델은 아래와 같은 단순한 선형회기 모델로 표현할 수 있다.

q′ = ω 0 ⋅ p′ + ω 1

(1)

학습 과정은 전체 학습 데이터를 표현하는 최적의 ω₀와 ω₁를 찾 는 것과 같다.

6. 실험 및 평가

대량의 데이터 생성을 위해 GMM 모델로부터 하나의 클러스터 마다 20,000개씩 총 100,000개의 시뮬레이션 파라미터 데이터를 샘플링하였다. 각 파라미터 샘플에 대해 CLO3D 시뮬레이터를 이용하여 정사각 드레이프를 시뮬레이션하고 테두리 벡터를 추 출하였다. 시뮬레이션에 사용된 가상의 옷감 시료는 최대 5mm 간격의 정점으로 구성된 메시 모델이며 시뮬레이션 시간 간격은 0.33 초로 하였다. 시뮬레이션 초기 상태는 그림 2와 같다. 시뮬레 이션 시작 후 모든 정점의 속도가 특정 임계치 아래로 떨어지면 시뮬레이션을 중단하였다. 떨림 현상으로 정점의 속도가 줄어들 지 않는 경우를 대비하여 4,000프레임 시뮬레이션 후에는 조건 없이 정지하도록 하였다. 100개의 CPU에 나누어 병렬 처리하였 고 약 42시간이 걸렸다. 시뮬레이션 결과가 발산한 것으로 판단 되는 일부 데이터는 제외하였다. 전체 데이터 중 무작위로 선택 된 10%는 테스트 데이터로 사용하고 나머지 90% 데이터를 학습 데이터로 사용하였다. 학습은 최소제곱법을 사용하여 식 1을 최 적화하였다.

6.1 시뮬레이션 파라미터 정확도

입력 벡터에 밀도를 포함하는 것에 대한 필요성을 확인하기 위 해 밀도를 제외하여 학습한 결과와 비교하였다. 표 3에서 첫 번째 행은 밀도를 제외하였을 때의 결과이고 두 번째 행은 밀도를 추 가하였을 때의 결과이다. 학습 데이터와 테스트 데이터에 대해서 평균제곱근오차 (root mean square error 또는 RMSE)와 결정계수 (R²)를 측정하였다. 평균제곱근오차는 0과 1 사이 값으로 정규 화된 데이터로부터 계산된 것이므로 절대 수치보다는 상대적인 차이에 의미가 있다. 밀도를 추가하였을 때 평균제곱근오차가 낮 아지고결정계수가 높아짐을 확인할 수 있다.

Table 3: Comparison of training results with and without density as input value.

Input type	Train RMSE	Train R²	Test RMSE	Test R²
without density	0.04557	0.86396	0.04908	0.84118
with density	0.03629	0.90878	0.03997	0.88908

Download Excel Table

표 4는 파라미터 별 학습의 정확도를 나타낸다. 테스트 데이터 에 대한 굽힘 강도 (BuK, BvK, BhK)의 R² 수치는 평균 0.97 이 상인데 비하여 신축성 강도 (Suk, SvK)와 전단 강도 (HK)는 평균 0.8 정도로 상대적으로 낮게 나타났다. 드레이프 모양을 분석해 보았을 때 굽힘 현상은 원기둥 윗면의 경계에서 직접 발생하지만 신축이나 전단 변형 등은 주름의 모양을 통해 간접적으로 표현되 기 때문으로 해석된다.

Table 4: Training results for each parameter.

Parameter	Train RMSE	Train R²	Test RMSE	Test R²
SuK	0.05188	0.82847	0.05597	0.80421
SvK	0.04943	0.81676	0.05331	0.78504
HK	0.04137	0.86395	0.04818	0.81548
BuK	0.01870	0.97867	0.02052	0.97374
BvK	0.01886	0.98192	0.02076	0.97771
BhK	0.01876	0.98293	0.02091	0.97833

Download Excel Table

6.2 드레이프 정확도

전체 테스트 데이터 중 200개를 무작위로 선택하여 결과의 시각 적 정확도를 검증하였다. 전체 결과는 논문과 함께 첨부된 보충 자료를 통해 확인할 수 있다. 그림 4는 그중 선택된 6개의 경우 를 나타낸다. “Ground Truth” 열은 테스트 데이터를 나타내고, “Predicted” 열은 테스트 데이터의 드레이프로 파라미터를 추정 한 후 다시 그 파라미터를 이용하여 정사각 드레이프를 시뮬레 이션 한 결과이다. “Contours” 열은 드레이프 결과의 오차를 시 각적으로 확인하기 위해 두드레이프의 테두리 벡터를 겹쳐 그린 것이다. 회색은 테스트 데이터 테두리 벡터이고 빨간색은 추정 된 파라미터로 계산된드레이프에서 추출한 테두리 벡터이다. 그 아래 숫자는 두 테두리 벡터 사이의 평균 오차를 mm단위로 나 타낸 것이다. 평균 오차는 두 테두리 벡터의 서로 대응하는 3차원 정점들 사이의 거리 차에 대한 평균이다.

Figure 4: Comparison between square drapes of ground truth and simulated from predicted parameters. No. 0 and 1 are chosen from those with a boundary error less than 5mm. No. 2 and 3 are chosen from those with a boundary error between 8mm and 10mm. No. 4 and 5 are the two worst cases among 200 randomly selected test data. “Contours” column presents overlapped pairs of boundary vectors and average contour errors. Gray one is from the ground truth and red one is from the predicted result.

Download Original Figure

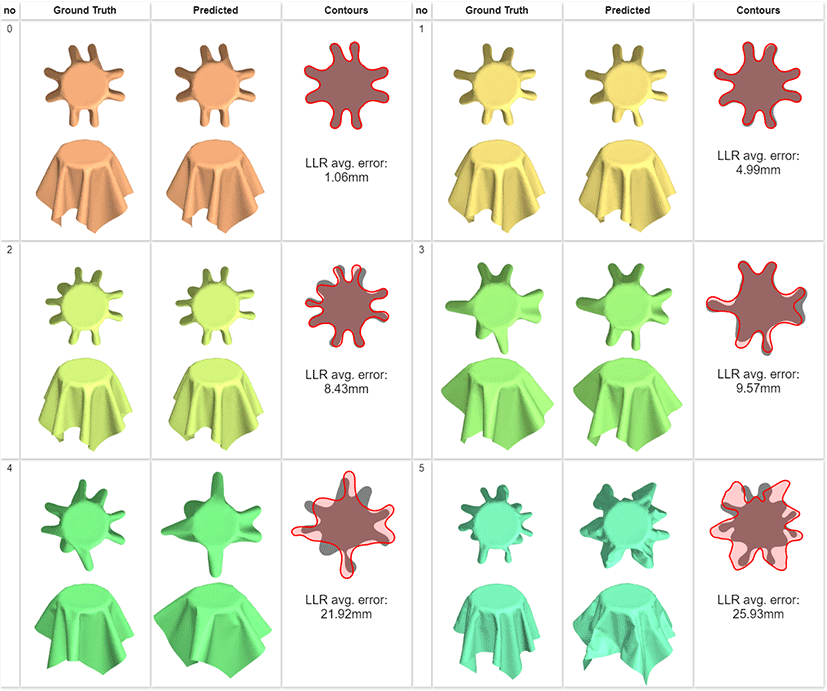
그림 4에서 0번과 1번은 평균 오차가 5mm 미만이 예이다. 평 균 오차가 5mm 미만일 때는 드레이프 모양에서 시각적 오차를 확인하기 어렵다. 2번과 3번은 평균 오차가 8mm에서 10mm 사 이인 경우이다. 드레이프 모양에서 시각적 오차를 확인할 수 있 지만, 전체적인 모양의유사도는 높다고 볼 수 있다.4번과 5번은 무작위 선택된 200개 중 오차가가장 큰 것과 그 다음으로 큰 것이 다. 오차가 큰 경우들의 전반적인 공통점은 테스트 데이터의 파 라미터가 GMM 생성 모델에서 낮은 확률로 샘플링된 것이라는 점이다. 예를 들어 4번의 경우 테스트 데이터의 Bvk가 30.21이고, 5번의 경우는 BvK가 67.62이다 (보충 자료 참조). 이 수치는 전 체 데이터의 평균값보다 크게 낮은 수치이다 (표 2 참조). GMM 모델의 기초 데이터로 사용한 400개의 실제 옷감 데이터가 실제 로 세상에 존재하는 옷감의 분포를 반영하는 것이라 가정하면 4 반과 5번은 존재 가능성이 낮은 옷감으로 가정할 수 있다.

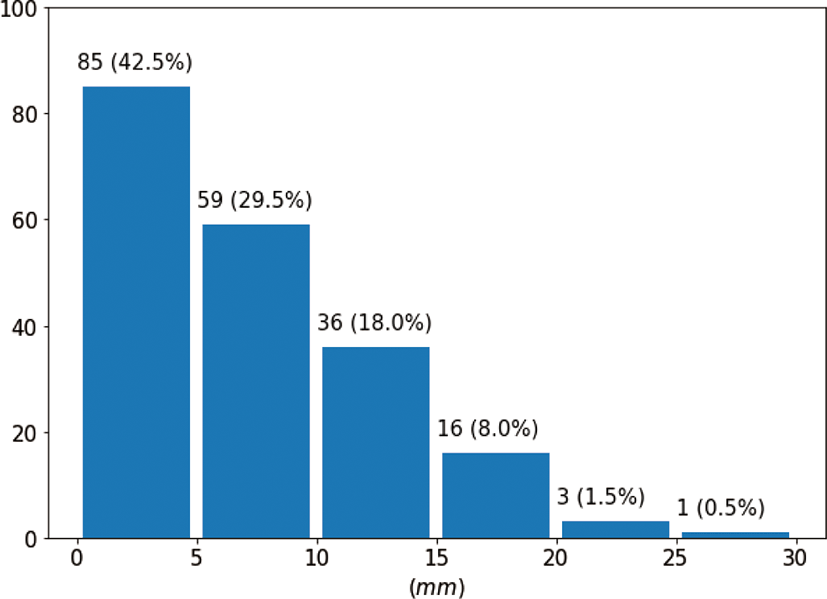
그림 5는 테두리 평균 오차를 5mm 간격 영역으로 구분하여 히 스토그램을 그린 것이다. 200개 중 평균 오차가 5mm 이하인 경 우는 42.5%로 나타났고, 평균 오차가 10mm 이하인 경우는 72% 로 나타났다. 평균 오차가 20mm 이상인 경우는 전체의 2%뿐 이다.

Figure 5: Histograms of boundary errors.

Download Original Figure

7. 결론 및 향후 과제

본 연구에서는 주어진 옷감 정적 드레이프를 보고 시뮬레이션 파 라미터를 예측하는 데이터 기반 학습 기술을 제시하였다. 시뮬레 이터는 CLO3D를 사용하였으며 정적 드레이프 형성에 높은 영향 을 미치는 6개의 파라미터를 대상으로 하였고, 대상 파라미터와 상관관계가 높은 쿠식 드레이프에서 착안한 정사각 드레이프를 사용하였다. 신뢰성 있는 학습 데이터를 대량으로 수집하기 위해 400개의 실제 니트 옷감으로부터 측정된 시뮬레이션 파라미터 집합을 기반으로 GMM 생성 모델을 만들고, 그로부터 새로운 파 라미터를 무작위로 샘플링하였다. 샘플 된 각 파라미터로 정사각 드레이프를 시뮬레이션하고 특징 벡터를 추출하여 학습 데이터 를 완성하였다. 학습 모델은 로그선형회기 모델을 사용하였다. 테스트 데이터를 이용한 실험 결과 높은 정확도를 나타냈으며, 시 각적 검증을 통해 추정된드레이프 모양과 원래 테스트 데이터의 드레이프 모양이 서로 유사한 경우의 비율이 높음을 증명하였다.

본 연구의 결과를 실용화하기 위해서는 실제 옷감의 드레이프 에서 특징 벡터를 추출하는 기술을 구현하고 검증하여야 한다. 실제 드레이프에서 테두리 벡터를 추출하기 위해서는 디지털 사 진으로부터 3차원 형상으로 복원하는 기술을 사용하거나 3차원 스캐너를 사용할 수 있다. 최신 모바일 장비는 깊이 측정 장치가 장착되어 있고 3차원 스캔 기능이 포함되어 있어 일반인도 쉽게 3차원 스캔을 할 수 있다. 향후 과제로 사용자 접근이 쉬운 3차원 스캐너를 이용하여 결과를 검증하는 실험을 진행할 예정이다.

본 연구는 시뮬레이션 데이터를 이용하여 학습한다는 점에서 Yang 등 [16]이 제시한 방법과 유사하다. 하지만 [16]에서는 각각 의 시뮬레이션 파라미터 수치를 직접 추정하는 대신 사전에 정의 된 52개의 대표 파라미터 집합 중 하나를 선택하도록 문제를 단 순화 하였다. 따라서 본 연구의 결과와 직접적인 비교는 어렵다. 향후 본 연구에서 제시한학습 모델을 수정하여 인공신경망 등을 이용한 옷감 분류 문제에 적용해보고 [16]와의 비교를 통해 유용 성을 검증해볼 수 있을 것이다.

학습 데이터 생성에서 기초 데이터로 사용한 400개의 옷감이 다양한 물성의 옷감을 포함하고 있지만 모두 니트 구조 옷감이 었다. 니트 구조 옷감과 우븐 구조 옷감은 서로 물리적 특성의 차이가 있는 것으로 알려져 있다. 향후 우븐 구조 옷감 데이터를 수집하고 현재 제시된 방법을 그대로 적용 가능한지 검증할 계획 이다. 필요에 따라 학습 모델을 구분하거나 니트와우븐 데이터를 동시에 학습 가능한 새로운 모델을 탐색해볼 계획이다.

실험 결과 신축성 강도의 학습 정확도가 굽힘 강도 학습 정확 도보다 상대적으로 낮은 것으로 나타났다. 정사각 드레이프의 신 축성 강도에 대한 표현력이 약한 것이 이유일 수 있으며, 또는 로그선형회기 모델의 한계일 가능성도 있다. 학습의 정확도를 높 이는 새로운 드레이프 방식과 비선형 학습 모델을 탐색해보는 것도 중요한향후 연구 주제이다.

본 연구에서는 실용성을 최대화 하기위해 오직 하나의 정적 드레이프만을 사용하여 파라미터를 추정하는 것을 목표로하였 다. 하지만 본 연구에서 제시하는 정사각 드레이프가 옷감의 모 든 물성을 표현하지 못 할 것이다. 정사각 드레이프가 표현하지 못하는 물성이 표현되는다른 정적 드레이프를 개발하고 복수의 정적 드레이프를 동시에 사용하여 파라미터를 추정한다면 표현 의 다양성을 높일 수 있을 것이다. 또한, 본 연구에서는 6개의 시 뮬레이션 파라미터만을 학습 대상으로 하였지만 비선형 옷감 시 뮬레이션 모델 [3]에서는 신축성 강도나 굽힘 강도를 각각 두개 이상의 파라미터로 표현하기도 한다. 향후 본 연구에서 제시한 방법을 CLO3D가 아니 다른 시뮬레이션 모델에 적용해보고 더 많은 수의 파라미터를 추정하는 것으로 확장해볼 계획이다.

감사의 글

연구에 중요한 아이디어를 제안해주신 (주)클로버추얼패션의 Jaden과 Robin에게 감사드립니다. 또한, 실험 데이터 제작에 도 움을 주신 Justin, Jack, Mason에게감사드립니다.

References

[1].

G. E. Cusick, “The dependence of fabric drape on bending and shear stiffness,” Journal of the Textile Institute Transactions, vol. 56, no. 11, pp. T596–T606, 1965.

[2].

K. S. Bhat, C. D. Twigg, J. K. Hodgins, P. K. Khosla, Z. Popović, and S. M. Seitz, “Estimating cloth simulation parameters from video,” in Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2003, pp. 37–51.

[3].

H. Wang, J. F. O’Brien, and R. Ramamoorthi, “Data-driven elastic models for cloth: modeling and measurement,” ACM transactions on graphics (TOG), vol. 30, no. 4, pp. 1–12, 2011.

[4].

E. Miguel, D. Bradley, B. Thomaszewski, B. Bickel, W. Matusik, M. A. Otaduy, and S. Marschner, “Data-driven estimation of cloth simulation models,” in Computer Graphics Forum, vol. 31, no. 2pt2. Wiley Online Library, 2012, pp. 519–528.

[5].

D. Mongus, B. Repnik, M. Mernik, and B. Žalik, “A hybrid evolutionary algorithm for tuning a cloth-simulation model,” Applied Soft Computing, vol. 12, no. 1, pp. 266–273, 2012.

[6].

S. Yang, Z. Pan, T. Amert, K. Wang, L. Yu, T. Berg, and M. C. Lin, “Physics-inspired garment recovery from a single-view image,” ACM Transactions on Graphics (TOG), vol. 37, no. 5, pp. 1–14, 2018.

[7].

J. Hu and Y.-F. Chan, “Effect of fabric mechanical properties on drape,” Textile Research Journal, vol. 68, no. 1, pp. 57–64, 1998.

[8].

T. Shyr, P. Wang, and K. Cheng, “A comparison of the key parameters affecting dynamic and static drape coefﬁcients of natural ﬁbre woven fabrics by a newly devised dynamic drape automatic measuring system,” Fibres and Textiles in Eastern Europe, vol. 15, no. 3, p. 81, 2007.

[9].

B. Al-Gaadi, F. Göktepe, and M. Halász, “A new method in fabric drape measurement and analysis of the drape formation process,” Textile Research Journal, vol. 82, no. 5, pp. 502– 512, 2012.

[10].

R. Sanad and T. Cassidy, “Investigating garment drape behaviour,” Journal of Fiber bioengineering and informatics, vol. 8, no. 1, pp. 47–56, 2015.

[11].

K. L. Bouman, B. Xiao, P. Battaglia, and W. T. Freeman, “Estimating the material properties of fabric from video,” in Proceedings of the IEEE international conference on computer vision, 2013, pp. 1984–1991.

[12].

W. Bi, P. Jin, H. Nienborg, and B. Xiao, “Estimating mechanical properties of cloth from videos using dense motion trajectories: Human psychophysics and machine learning,” Journal of vision, vol. 18, no. 5, pp. 12–12, 2018.

[13].

S. Kawabata, “The standardization and analysis of hand evaluation,” in Effect of mechanical and physical properties on fabric hand. Elsevier, 2005, pp. 389–442.

[14].

D. E. Breen, D. H. House, and M. J. Wozny, “Predicting the drape of woven cloth using interacting particles,” in Proceedings of the 21st annual conference on Computer graphics and interactive techniques, 1994, pp. 365–372.

[15].

A. Davis, K. L. Bouman, J. G. Chen, M. Rubinstein, F. Du-rand, and W. T. Freeman, “Visual vibrometry: Estimating material properties from small motion in video,” in Proceedings of the ieee conference on computer vision and pattern recognition, 2015, pp. 5335–5343.

[16].

S. Yang, J. Liang, and M. C. Lin, “Learning-based cloth material recovery from video,” in Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 4383– 4393.

[17].

E. Carrera-Gallissà, X. Capdevila, and J. Valldeperas, “Evaluating drape shape in woven fabrics,” The Journal of The Textile Institute, vol. 108, no. 3, pp. 325–336, 2017.

[18].

A. Lam, A. Raheja, and M. Govindaraj, “Neural network models for fabric drape prediction,” in 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), vol. 4, 2004, pp. 2925–2929.

[19].

M. Halász, “Sylvie® 3d drape tester–new system for measuring fabric drape,” 2006.

[20].

N. Kenkare, T. A. Lamar, P. Pandurangan, and J. Eischen, “Enhancing accuracy of drape simulation. part i: Investigation of drape variability via 3d scanning,” Journal of the Textile Institute, vol. 99, no. 3, pp. 211–218, 2008.

[21].

V. Glombikova and K. Zdenek, “Drape evaluation by the 3d drape scanner,” Tekstil ve Konfeksiyon, vol. 24, no. 3, pp. 279–285, 2014.

[22].

A. Hussain, Y. Zhong, T. Naveed, Z. Yu, Z. Xi, and W. Ge, “A new approach to evaluate fabric hand based on three-dimensional drape model,” Autex Research Journal, vol. 20, no. 2, pp. 155–167, 2020.

[23].

CLO Virtual Fashion Inc., “CLO,” https://www.clo3d.com/, 2009–2020.

[24].

D. Baraff and A. Witkin, “Large steps in cloth simulation,” in Proceedings of the 25th annual conference on Computer graphics and interactive techniques, 1998, pp. 43–54.

[25].

CLO Virtual Fashion Inc., “Fabric kit manual,” https://support.clo3d.com/hc/en-us/articles/360041074334-Fabric-Kit-Manual, January 2020.

[26].

H. Akaike, “Information theory and an extension of the maximum likelihood principle,” in Selected papers of hirotugu akaike, 1998, pp. 199–213.

< 저자소개 >

주 은 정

jkcgs-26-5-15-g6

2004년 연세대학교 컴퓨터공학과 학사
2010년 서울대학교 컴퓨터공학부 박사
2011년 서울대학교 컴퓨터연구소 박사후 연구원
2012년 한국과학기술연구원(KIST) 실감교류로보틱스 센터 박사후 연구원
2013~2017년 삼성전자 DMC 연구소 및 영상 디스플레이 사업부 책임 연구원
2018년~현재 클로버추얼패션 기술이사
관심분야 : 컴퓨터 그래픽스, 캐릭터 모델링/ 애니메이션, 모션데이터 러닝

최 명 걸

jkcgs-26-5-15-g7

2004년 경북대학교 컴퓨터공학과 학사
2010년 서울대학교 컴퓨터공학부 박사
2011년 JST ERATO Design Interface Project 박사후 연구원
2012년~2013년 IPAB, Edinburgh University 박사후 연구원
2014년~현재 가톨릭대학교 미디어기술콘텐츠학과 미디어공학전공 교수
관심분야: 컴퓨터 그래픽스, 캐릭터 애니메이션, 가상현실, 데이터 기반 시뮬레이션