주 관절 경로의 변형을 통한 걷기 동작 수정

하나의 모션 데이터를 이용하여 모션을 변형하는 방법은 프레임 간의 관계를 이용한다. [5] 는 캐릭터의 계층적인 구조를 이용하 여 모션을 변형하였고, [3, 6] 은 모션을 주변 환경이나 다른 캐릭 터와의 관계를 이용하여 변형하였다. 또 [7] 은 물리 모델을 도입 하여 모션을 변형하였다. 여러 모션 데이터의 각 프레임 사이의 관계를 이용하여 변형 및 합성 방법으로 새 모션으로 만드는 방법 이있다. [1, 8] 은 모션 데이터의자세간 차이를 비교하여 유사한 자세를 간선으로 정의한 그래프로 해석하였다. 캐릭터의 상태는 자세와 위치로 정의되며모션을 생성하는 것은 하나의 상태에서 다른 상태으로 이동하는 것에 대응된다. 그러므로 원하는 상태에 도달하는 모션을 생성하기 위해서는 시작 상태에서 그래프 탐색 을 수행하여 정점 리스트를 구하여야 한다. 이 방식은 그래프의 연결성에 따라 성능이 결정되는데, 각 정점과 연결되는 간선의 수가 적으면 목표 상태로의 탐색이 어렵다는 것과 간선의 수가 많으면 탐색 시간이 느려진다는 점이 서로 상충된다. 이 점을 해 결하기 위해 유사한 간선 사이에 연속적인 새 간선을 보간하는 연구 [9, 10] 가 진행되었다. 본 연구는 기존의 간선으로 표현되는 모션을 변형하여 새 간선을 만드는 방법이다. 학습을 통해 입력에 따라 연속된 자세를 생성하는 방법 [11, 2, 12, 13, 14] 들도 연구 되었다. 이들은 비선형 공간으로 모션 데이터들을 변환하고 이 공간에서 자세 간 관계를 추출하였다. 원하는 목표 동작을 만들 기 위해 비 선형 공간에서의 이동을 학습하여 새 동작을 생성하 였다. 또한 한정된 크기의 동작 데이터에서 목표 상태까지의 이 동을 보장하기 위해서는 추가 학습을 필요로 하였다. 본 논문이 제안하는 방법은 추가적인 동작 데이터나 학습 없이, 걷는 동작에 한해 원하는 목표 상태를 달성할 수 있다. [15]에서는 환경에 따 른 3차원 경로를 수정하여 모션을 보간하는 연구를 진행하였다. 위 연구에서 주 관절의 경로를 변형하기 위해 3차원의 전역 좌 표계를 사용하였는데, 이와 다르게 이 연구에서는 전 프레임으로 정의되는 지역 좌표계를 사용함으로써 경로의 회전에도 직관적 인 스타일을 유지할 수 있도록 하였다.

[3, 16] 에서는 모션 변형을 위하여 캐릭터 상태의 각 조인트의 위치와 환경과의위치를 연결한 메쉬로 표현하였고, 이를 그래프 라플라시안으로 변형하였다. 본 논문 또한 모션 변형을 위하여 그래프 라플라시안 연산자를 이용하며 [17] 에서 제안하는 메쉬 변형법을 이용하고 있다. 이 연구는 메쉬를 그래프의 형태로 나 타내고 여기에 행렬을 곱하여 그래프 정점을 주변 정점과의 관 계로 표현하는 공간(Differential coordinate)으로 변환한다. 이 변 환된 좌표를 다시 3차원 공간(Cartesian coordinates)으로 변환하 기 위해서는 제약 조건이 필요하며 이를 최소자승법(least square method)으로 복원하게 된다. 여기에서 구해진 해는 제약조건에 따라 달라지는데 주변 정점과의 관계를 최대한 유지한 채로 제 약조건을 만족하게 되므로 세밀한 정보는 유지하고 전체적인 정 보를 변형하는 결과를 얻게 된다. 또한 이 연구에서는 정점의 위 치만 고려하지 않고 법선 벡터를 함께 고려하므로 곡선에 대한 변형도 고려할 수 있게 되었다. 본 논문은 이러한 변형 방법을 주관절 이동경로에 적용하였다. 각 프레임의 주관절 위치를 정점 으로 하고 주변 프레임의 위치를 이어주는 간선을 가진 그래프로 표현하였고 이를 같은 라플라스 행렬로 공간 변환을 수행하였다. 또한 주관절의 방향(캐릭터가 향하는 곳)을 함께 고려하여 동작 변형 시 목표 캐릭터 방향도 지정할 수 있게 하였다. 목표 방향에 따라 중간 이동 경로 또한함께 변형함을 확인하였다.

이장에서는 제안하는 방법을 설명하기 위해 먼저주관절 경로를 정의한다.

χ_t 는 프레임 t 의 경로의 전역 좌표계 w의 좌표값들로 정의 된다. 모션 M에는 각 χ_t를 기준으로 캐릭터 주 관절의자세가 기 록되어 있다. 이 자세들은 y 축이 캐릭터의 위쪽 방향(중력 반대 방향)으로, z 축은 캐릭터의 앞 방향으로 정렬되어 있다. 여기에 우리는 각 χ_t마다 상태 벡터 v_t 를 정의하였다 (Figure 1).

Figure 1: The state of root joint trajectory. y_w represents a height from the ground and x_l, z_l are coordinates seen from the root frame at the previous frame. To deal with the direction of the trajectory, θ is the difference between the tangent of the trajectory and z. (a) and (b) shows the same points at the different viewpoints for the explanation.

Download Original Figure

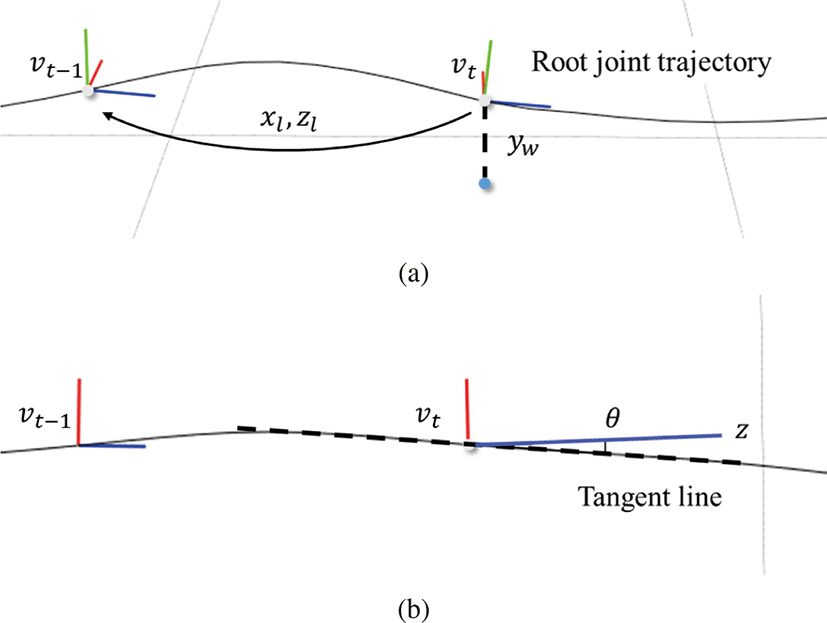
상태 벡터에서 y_w 는 전역 좌표계의 값이고, x_l과 z_l은 지역좌 표계에서 보는 x, z 값이며, θ 는 주 관절 경로의 접선벡터와 주 관절의 z 벡터사이의 각도이다. 이 각도는 관성좌표계의 y 축의 값으로만 표현한다. 모든 프레임의 상태 벡터는 행렬 V 로 표현 가능하다.

v_t 의 지역좌표계는 t − 1 프레임의 주 관절 자세와 같다. 우리 는 상태 벡터로부터 그래프 G를 정의할 수 있다. 각 정점은 상태 벡터 v 이며 간선은 주변 프레임의 상태 벡터를 연결한다.

우리는 정의된 그래프로부터 도출할 수 있는 변이 값(differential coordinates, δ)을 정의하였다.

이 값은 한 정점 v 를 그의 주변 프레임 neighbor(v)으로 기술 하는 것이며, 또한 주변 정점과의 관계를 나타내어 지역적 모양 정보를 포함한다. 예를 들면, v가 메쉬(mesh) 위의 정점을 나타낸 다면 δ는 v의 주변 정점들의 중점과 v의 상대 위치로 표현된다. 이는 δ 가 v 의 곡면 정보(법선 벡터 및 곡률)를 추정한다고 볼 수 있다. V 로부터 δ를 구하기 위해서 다음과 같은 선형변환 L (그래프 라플라시안연산자)을 정의할 수 있다.

I 는 단위행렬이고 D는 띠행렬(band matrix) 로 대각 성분의 위아래의 값이 1로 채워져 있다.

구해진 L을이용한다면

로 표현할 수 있다. 여기에서 L의 역행렬을이용하면 δ로 부터 상태 벡터 v를 다시 얻을 수 있지만 L의 계수(rank)가 부족하므로 이를 위해선 추가적인 항이 필요하다. 우리는 이 부분에 목표하는 제약 조건c을 추가함으로써 계수를 증가시키고, 원하는 형태로 변형된 상태 벡터 v′을 구할 수 있다. 만약 추가되는 제약 조건이 1개 이상이라면 이는 해가 없는 상태 (over-determined) 가 되는데 이를 해결하기 위해 최소자승법(weighted least-square method)을 이용하여 V 를 구한다. c 를 추가하여 v′를 얻는 방법은 다음 항에 서설명한다.

여기에서는 제약 조건을이용하여 주관절 경로를 구하는 것을 보 여준다. 여기에서 제약 조건은 주관절의 상태 v 위에 설정된다.

제약 조건을 고려한해를 구하기 위해행렬 A 를 정의한다.

S_t ∈ ℝ^1×T 는 선택 행렬로 t 열에 1 이고 이외의 열에는 모두 0을 가진다. 여기에서 우리는 0, T 번째 프레임에 목표를 설정할 것이다.

L과 함께 S는 연립 선형 방정식을 이룬다. 위의 행렬 A는 제 약 조건을 0과 T 프레임에 설정하였다. 이를 이용하여 해 v^* 를 구하려면

의 식을 이용한다. A^†는 A행렬의 의사역행렬(pseudo inverse) 이다. b(δ, c) 는 복원하기 위한 원 모션의 δ 값과 A에서설정한 0, T 번째 프레임의 목표 상태 c₀, c_T 를 쌓은 형태의 행렬이다.

위와 같이 목표하는 경로 v^*를 구할 수 있다. 여기에서 상태벡 터의 x_l, z_l 는 지역좌표계로 정의되어 있다. 지역좌표계는 이전 프레임으로 정의되어 있으므로 x_l, z_l 의 값 또한 이전 프레임에 종속된 함수로 생각할 수 있다. 이로인해, 직관적으로 역행렬을 이용하여 해를 구하는 것으로 정확한 해를 구할 수 없게 된다. 이를 해결하기 위해 우리는 지역적인 범위에서는 선형이라는 조 건을 추가하여 반복적인 방법(iterative method)로 비선형의 해를 구하였다. 우선 목표 경로 χ*에 근접하기 위해 제약조건 c를 구 하여야 한다. 이전 상태 벡터를 v⁻라고 정의하고 이와 대응되는 경로는 χ⁻라 하자. 이 경로를 구하기 위해서는 지역좌표계로 정 의된 x_l, z_l를 전역 좌표계 x_w, z_w로 변환해야 한다. χ⁻와 χ^*로 부터 c를 구하는데, 비선형성을 고려하여 χ⁻의 목표를 최대 α 값 만큼만 차이 나도록한다.

위에서 구해진 c를 식 13에 대입하여 새로운 해 v′를 구한다. 이 과정을 v′가 목표에 도달할 때까지 반복한다.

변형된 주 관절 경로에 적합한 모션을 생성하기 위해서 우선 모 션 데이터의 환경과의 접촉점 정보를 추출한다 [18]. 이는 차후 모션 변경시 접촉점과 환경과의 접촉시 밀림 현상을 제거하기 위 한 정보로 사용된다. 모션 생성을 위해 우선 모션 데이터의 주 관절 경로를 구해진 해(V*)로 대체한다. 그리고 접촉점 최적화 기법[16] 을이용하여 생성된 각 관절의 경로를 부드럽게 유지하 면서 접촉점을 유지하는 모션을 생성한다. 위의 과정을 다음의 알고리즘으로 정리하였다.

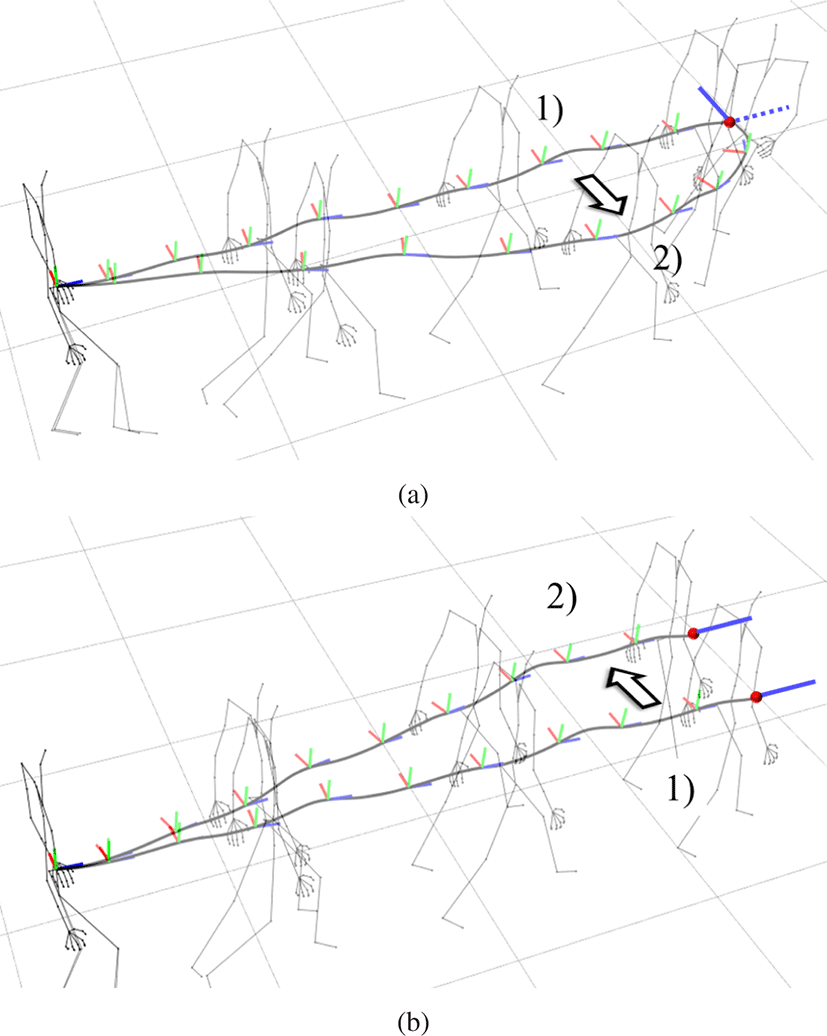
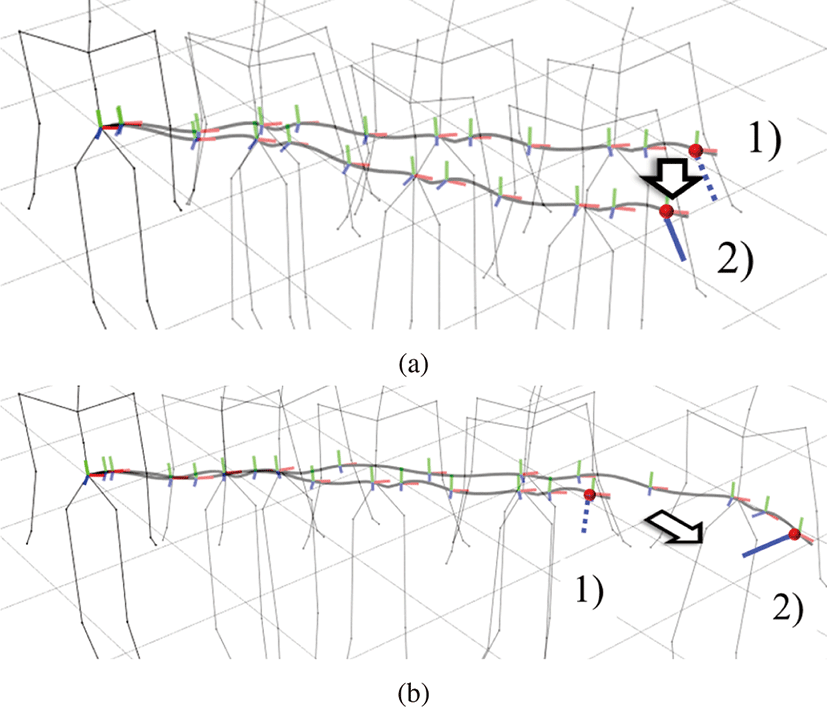
변형에 사용한 동작 데이터는 직선으로 걷기와옆으로 걷기 동작 을이용하여 실험을 진행하였다. Figure 2 는 직선으로 걷는 동작 이며 데이터의 끝 (프레임 T)에 변형 조건을 설정하였다. Figure 2(a)는 도착 위치는 같지만 방향은 90도 회전을 하였다. 주관절 경 로의 스타일을 유지하면서 마지막 회전조건을 만족하기 위해 중 간경로가 회전 반대 방향으로 휘어져 있는 것을 확인할 수 있다. 만약 경로가 후반의 적은 프레임만 조건을 만족시키기 위해 회 전한다면 δ에 의해 발생되는 오차값이 커진다. 우리는 자승법에 의해 오차를 줄이므로 오차값이 경로 전반으로 퍼져나가게 되어 위와 같은 형태로 최종 수렴한다. Figure 2(b)에서는 회전 방향을 고정한 채로 위치를 옮겼을 때의 결과를 보여준다. 또는 회전과 이동 조건을 동시에 만족하는 경로를 구할 수도 있다. Figure 3 는 옆으로 걷는 동작의 변형을 보여준다. 직선 걷기와는 다르게 주관절의 방향이 걷는 방향과 서로 수직에 가깝다. 우리는 주관절 상태 벡터 v를 정의하면서 경로와 주관절 방향의 차이 θ를 정의 했으므로 이러한 동작도 변형가능하다. Figure 3(a) 의 경우에는 최종 프레임의 주관절 위치만 이동시킨 결과이다. 주관절 방향은 유지한채 경로만 변형된 것을 확인할 수 있다. 또한 관절 경로의 형태가 변형후에도 비슷한 것을 보이는데 δ 값으로 스타일이 유 지되었다는 것을 알 수 있다. Figure 3(b) 는 위치와 방향이 동시에 변형된 결과를 보여준다. 좀더 길어지고 방향도 틀어졌는데, 이 럴 경우 발이 바닥에 쓸리는 현상(Foot skate)이 발생할 가능성이 높다. 하지만 후처리에서 접촉점을유지하기 위해 접촉점 최적화 기법[16]을이용하므로 이런 이상현상을 최소화하였다.

Figure 2: The result of the editing that deforms the walking motion in the straight. (a) shows when the final pose is rotated about 90°, and (b) shows when the final position is moved.

Download Original Figure

Figure 3: The result of the editing that deforms the side walking motion. (a) shows when the final pose is moved, and (b) shows when the final position and the direction are modified.

Download Original Figure

실험에는 Intel i5-9500F CPU 가 장착된 컴퓨터를 사용하였으며, 각 실험에 데한 데이터는 Table 1 에 정리하였다. 종료 조건인 ∈은 0.01로 설정하였다. 위치에 대한 조건만 있을 경우 1번에 만족하 게 되지만 방향에 대한 조건이 추가되면 여러번의 반복이 필요한 것을 볼 수 있다.

4.1.1 강건성에 대한 실험

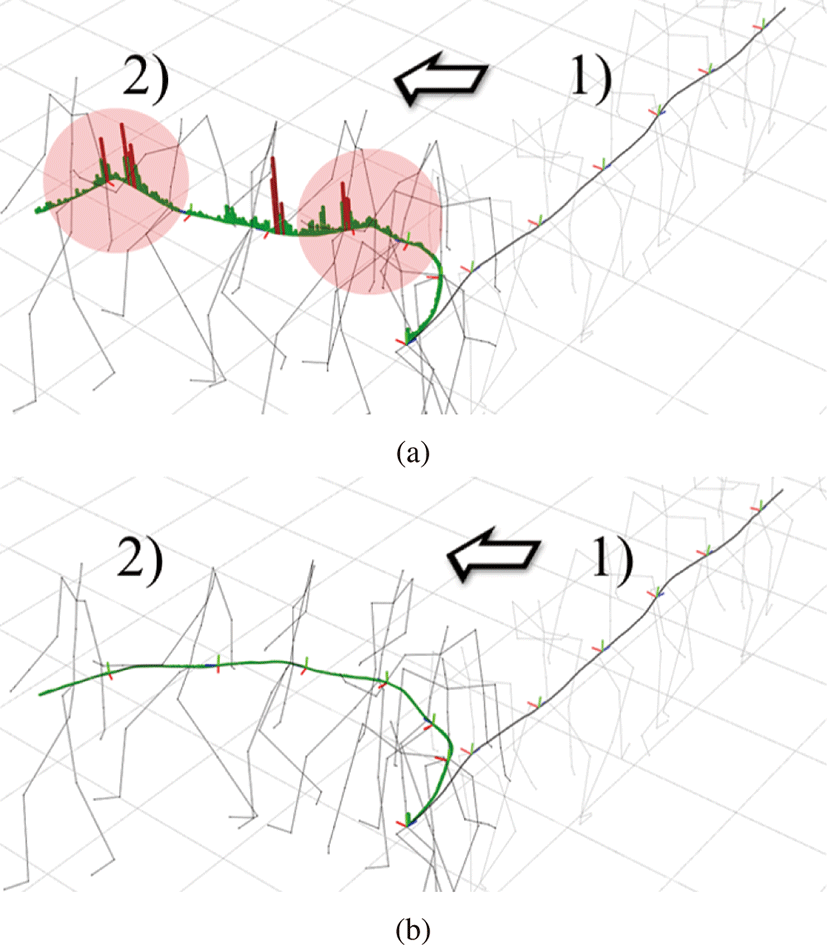
이 절에서는 제시하는 변형 방법의 강건성을 실험하기 위해 목표 지점을 기존 도달 지점과 180도 회전하여 도달하도록 하였다. 또 한 올바른 결과를 얻기 위하여 도달 위치는 시작점에서 좌측으로 이동하였다. 실험을 통해 Figure 4(a)에서 강조된 영역과같이 주 관절 경로가 급격히 변형되는 모습을 볼 수 있다. 이는 |δ| 의 값과 연관되어 있으므로 Figure 4(a)의 경로에 |δ| 값을 막대 그래프로 표현하여 |δ| 값이 급격히 변화하는 부분을 붉은 색 막대 그래프로 구분하였다. 이에 따라 주 관절 경로가 급격히 변화하는 부분과 |δ| 값이 급격히 변화하는 부분이 유사하게 나타난다는 것을 알 수 있다. 따라서 δ 값이 급격히 증가하는 것을 방지하기 위하여 B-스플라인 보간법 [19]을 사용하여 δ의 값을 경로 전체에 걸쳐 서 완화하였다. 이러한 결과 기존에 기대했던 Figure 4(b)가 됨을 확인하였다.

Figure 4: (a) is the result of the deformation when the target is turned to 180°, which makes the motion more deforming than other experiments. We highlight the artifacts on the trajectory with the red circle. The bar on the trajectory represents |δ| where a higher bar is a higher value. To handle this problem, we interpolate the trajectory as the B-Spline, and apply the deformation. (b) shows the result after the interpolation.

Download Original Figure

또한 동작을 변형하기 위한 Algorithm 1 단계별 소요 시간을 측 정하였다. 실험에 사용된 동작은 총 316프레임으로 약 2.6초의 데이터를 담고 있다. 이 실험에서 해를 구하기 위해서 14라인의 반복문을 3번 수행하였다. Algorithm 1 의 6번 줄부터 9번 줄은 초기화 부분으로 약 4.5 밀리초가 소요 되었다. 반복문에서 15번 줄은 경로를 복구하는 것으로 약 3.1 밀리초가 소요되었으며 16 번 줄은 제약 조건을 설정하는 것으로 약 0.1밀리초 소요되었다. 17번 줄은 희소행렬의 역행렬을 구하여 해를 구하는 것으로 약 0.8 밀리초가 소요되었다. 이는 초기화를 제외하고 많은 시간을 경로 재 구축하는 것에 쓰임을 알 수 있다.

본 논문에서 제안한 동작 변형 방법을 모션 그래프 탐색에 적용 하여 복잡한 환경에서도 목표 동작을 만족하는 경로를 구할 수 있게 한다. 2장에서 언급했듯, 모션 그래프는다른 상태로 전이할 수 있는 간선이 충분해야 목표에 도달하는 경로를 구할 수 있지 만, 반대로 많은 간선을 탐색하기 위해선 탐색시간이 늘어나므로 해결 방법이 필요하게 된다. 제안한 모션 변형을 이용하면 적은 모션으로도 넓은 범위의 모션을 가진 것 같은 효과가 있으므로 간선을 늘리지 않아도 해를 찾을 수 있게 해준다. 이는 특히 해를 찾기 어려운 환경 (예, 복잡하고 좁은 통로)에서도 경로를 찾을 수 있게 해준다.

4.2.1 모션 데이터

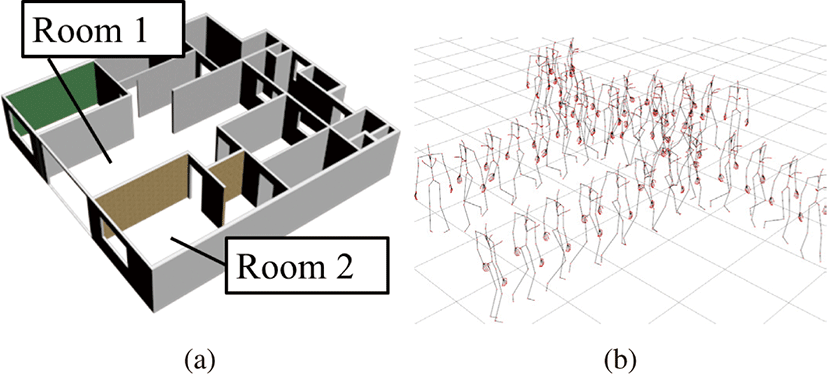
실험에 사용된 동작 데이터는 약 90초 정도의 걷기 행동이 담겨 있으며 (Figure 5(b)) 캐릭터는 65개의 관절과 총 162개의 관절 자 유도(Degrees of Freedom)를 가지고 있다. 이는 손가락 관절과같 은 세밀한 움직임을 나타내는 모든 관절을 포함한 것이다. Figure 5(b) 과 같이 동작 데이터는 일정 넓이의 공간을 무작위로 걷는 동작이 촬영되어 있으며 이를 30Hz 로 처리하여 사용하였다. 이 데이터에서 모션 그래프를 생성하였으며 그래프 탐색은 A* 알고 리즘을 이용하였다. 캐릭터가 걸어다닐 환경은 Figure 5(a)와 같 이 방과 방이 연결된 주거 공간으로 방과 방 사이 통로는 약 1.2m 의 너비를 가진다. 우리는 모션 그래프를 이용하여 방 1(Room 1) 에서 방 2(Room 2)로 이동하는 동작을 생성한다. 캐릭터는 방1 에서 의자에서 일어난 후에 걷기 모션을 통해 방 2로 이동한 후 침대에 눕는다. 이 사이 걷기 동작을 생성해야 하므로 동작의 양 끝의위치와 자세는 지정되어 있다.

Figure 5: (a) The house model as the environment, in which the searching is performed. (b) The source motion for generating the motion graph.

Download Original Figure

4.2.2 그래프 탐색과 모션 변형 방법의 적용

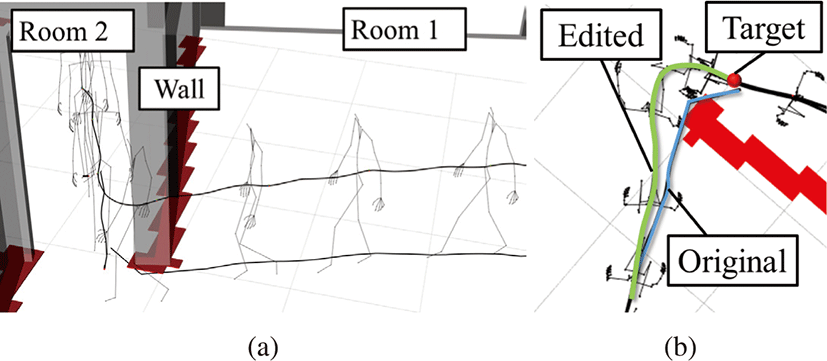
방1에서 캐릭터가 의자에서 일어나는 동작(동작 1)과 방 2에서 침대에 눕는 동작(동작 2)을 연결시키기 위해서 그 사이의 걷는 동작을 생성시키고자 한다. 그러기 위해서 동작 1의 마지막 위 치와 자세를 캐릭터의 시작 상태 v_s로 정의하고 동작 2의 시작 위치와 자세를 종료 상태 v_t 로 정의한다. 우선 모션 그래프를 탐 색하여 v_s를 시작 상태로 하여 목표 상태 v_t 까지의 경로를 구할 수 있는지 확인한다. 탐색은 v_t 에 충분한 범위 내에 있을 때 종 료하게 된다. 실험에서 탐색 종료 조건은 위치와 방향이 50cm, 45° 이하로 설정하였다. 탐색 결과는 갑자기 캐릭터가 이동하는 부자연스러운 동작이 된다(Figure 6(b)). 이를, 제안한 동작 변형 방법을 적용하여 부드럽게 연결되는 최종 동작을 생성한다. 이 방 법은 단순히 위치뿐만 아니라 방향도 보정할 수 있으며 δ에 의해 경로 전체에 오차값이 전달되어 부드러워 지면서도 스타일을 보 존 하는 동작이 생성된다. 만약 경로가 더욱 복잡할 경우, v_s와 v_t 사이에 중간 목표 지점을 추가하여여러 경로로 나누어 탐색하여 해결할 수 있다.

Figure 6: The result of the motion graph that combined with our deforming method. The path starts from room 1 and ends at room 2 that the character must pass through the door, which is narrow. (a) is the perspective view of the motion. Also, (b) is the top view, and the original trajectory is not continuously connected to the target. Our method can connect smoothly two ends despite the mismatch between angles.

Download Original Figure