1. 서론
인간 형상을 갖는 물리 기반 캐릭터는 그 동역학이 복합하고 동작 제어에 있어서 작은 오차에도 쉽게 넘어지기 때문에 그 동작을 안정적으로 제어하는 것은 일반적으로 쉽지 않은 문제이다. 하지만 최근 몇 년간 딥러닝 기술을 통해 물리 기반 캐릭터의 동작을 안정적으로 다룰 수 있는 제어기를 생성하는 심층 강화학습(deep reinforcement learning) 기법들이 제안되어 왔다[1,2,3,4,5]. 이러한 비지도학습(unsupervised learning) 기법들은 캐릭터가 반복적으로 시뮬레이션 환경과 직접 인터랙션 하면서 제어기를 개선시켜 가기 때문에 별도의 학습 데이터를 필요로 하지 않지만 최적의 제어기를 탐색하는데 있어서 수많은 시뮬레이션이 필요하기 때문에 많은 계산 비용 발생한다. 반면, 지도학습(supervised learning) 기법의 경우, 제어기를 학습하는 동안 별도의 시뮬레이션이 필요하지는 않기 때문에 학습 시간을 많이 절약할 수 있지만, 좋은 성능을 갖는 제어기를 생성하기 위해 적절한 학습 데이터를 어떻게 수집해야 하는지가 자명하지 않다.
이 문제를 다루기 위해, 본 논문에서는 확률적 모델예측제어 (model predictive control) 기법을 이용하여 지도학습에 필요한 학습 데이터를 간편하면서도 효과적으로 생성하는 기법을 제안한다. 또한 이렇게 생성된 학습 데이터를 빠르게 학습할 수 있는 인공 신경망 학습 방법도 제안한다. 모델예측제어는 캐릭터 동작에 대한 동역학 모델을 기반으로 실행시간에 캐릭터의 현재 상태로부터 시작하여 비교적 가까운 미래를 예측하여 최적의 현재 제어 입력을 선택하는 온라인 근거리 궤적 최적화 기법(short-horizon trajectory optimization)이다. 다시 말하면, 실행시간에 현재 시점으로부터 1-2초 정도의 가까운 미래까지의 시간 윈도우를 주기적으로 시간의 흐름에 따라 이동시키면서 그 시간 윈도우 안의 동작을 예측하여 캐릭터에 적용되는 제어 입력을 최적화 시키는 기법이다. 이러한 온라인 특성으로 인해 모델예측기법은 외란(external disturbance)이나 캐릭터의 다양한 역학적 상태에 대해 강인하게 반응할 수 있지만 예측에 기반한 제어 입력의 주기적인 재계산은 상당한 계산 비용을 필요로 하여 실시간 성능을 얻기가 쉽지 않다. 본 논문에서는 이러한 계산 시간을 줄이기 위해 실행시간 시뮬레이션에서 모델예측제어를 사용하는 대신, 기존의 모델예측제어 기법[6]에 확률적인 요소를 추가하여 물리 기반 제어기에 대한 지도 학습을 위해 필요한 다양한 학습 데이터들을 효과적으로 수집하고 그 수집된 데이터를 정규화 하여 인공 신경망을 학습하는 방법을 제안한다. 기존의 딥러닝 기반의 강화학습 기법이 보행 제어기를 생성하는데 수 일이 걸린 것에 비해[1], 본 논문에서 제안하는 지도 학습 기법은 걷기 동작과 달리기 동작에 대한 보행 제어기를 1-2시간 안에 학습할 수 있다.
본 논문의 공헌은 다음과 같다. 첫째, 확률적 모델예측제어 기법을 통해 학습 데이터를 빠르고 효과적으로 생성하는 기법을 제안한다. 기존의 모델예측제어 기법에 대한 간단한 확장을 통해 물리 기반 시뮬레이션에서 캐릭터를 안정적으로 제어할 수 있는 학습 데이터를 효과적으로 탐색할 수 있다. 둘째, 이렇게 수집된 학습 데이터를 가지고 제어기를 효과적으로 생성하기 위한 인공 신경망 학습 프레임워크를 제안한다.
본 절 이후, 2절에서는 물리 기반 캐릭터 애니메이션에 대한 관련 연구들에 대해 살펴보고, 3절에서는 본 논문에서 제안하는 시스템의 전체적인 구성에 대해서 소개한다. 4절에서는 확률적 모델예측제어 기법을 통해 학습 데이터를 수집하는 방법에 대해 설명하고, 5절에서는 이렇게 수집된 데이터에 기반하여 인공 신경망을 학습하는 방법을 다룬다. 6절에서는 제안된 시스템에 대한 실험결과를 제공하고 7절에서는 한계점과 향후 연구에 대해 논하며 본 논문을 마무리 짓는다.
2. 관련 연구
캐릭터 애니메이션 분야에 da Silva와 그의 동료들이 모델예측제어 기법을 도입한 이래로[7], 이 기법은 물리기반 캐릭터의 동작을 안정적으로 제어하는데 효과적으로 사용되어 왔다[6,7,8, 9,10,11,12,13,14,15,16,17,18]. 모델예측제어 기법은 선 자세(standing pose)에 대한 균형잡기[9,10], 다양한 보행 동작[7,8,11,14], 기계체조 동작[6,12], 복잡한 지형에서의 보행 동작[13], 축구 동작[17], 시각과 운동이 결합된 동작[18] 등과 같이 다양한 동작에 성공적으로 적용되어 왔다. 예제 데이터 없이 동작을 생성하는 모델예측제어 기법[8,9,10,16]은 다양한 동작을 자동적으로 생성할 수 있지만 그 동작이 일반적으로 자연스럽지 못하여 예제 데이터를 안정적으로 추적하는 모델예측제어 기법이 또한 활발하게 제안되어 왔다 [7,11,12,13,6,14,15,17,18]. 그 외에도 예제 동작을 캐릭터의 현재 상태에 따라 최적 제어를 통해 자동으로 타임워핑(time warping)하는 모델예측제어 기술이 제안되었다[15].
일반적으로 전신(full-body) 캐릭터는 높은 자유도를 갖고 그 동역학이 복잡하기 때문에 모델예측제어를 수행하는 데는 많은 계산 시간이 소요된다. 이 문제를 다루기 위해 수치적 미분에 대한 병렬처리[9], 저차원 모델예측제어[8,14], 완화된 접촉 동역학[9] 및 물리량 재사용 기반의 가속 기법[6], 근사된 동역학에 기반한 분석적 미분을 이용한 모델예측제어 기법[16] 등이 제안되어 왔다.
Levine과 그의 동료들은 Differential Dynamic Programming (DDP)[19]을 통해 생성된 최적 제어 정책(optimal control policy)들로 인공 신경망을 초기화 시키고 policy search에서 그 신경망의 성능을 개선시키는 Guided Policy Search (GPS)라는 기술을 제안하였다[20]. Zhang과 그의 동료들은 모델예측제어를 통해 드론(drone)의 전체 상태에 대한 관측이 가능할 때의 제어기를 초기화 시키고 policy search를 통해 드론의 일부 상태 관측에 기반한 제어기로 적응시키는 방법을 제안하였다[21]. 본 연구는 모델예측제어를 통해 인공 신경망의 학습 데이터를 생성한다는 점에서 앞의 기존 연구[20,21]와 유사하지만, 추가적인 policy search 없이 간단하면서도 효과적으로 학습 데이터를 생성하여 지도 학습만으로 캐릭터 동작을 안정적으로 생성하는 제어기를 학습하는 기법을 제안한다.
심층 인공 신경망과 강화학습을 결합한 심층 강화학습은 다양한 동작을 효과적으로 수행하면서 여러 환경 변화에도 강인하게 반응하는 실시간 제어기를 성공적으로 생성하였다. 최근 몇 년간, 비디오 또는 예제 데이터 모방[1,22], 농구 드리블 동작 수행[17], 근육 모델에 기반한 캐릭터 동작 제어[3], 시각에 기반한 캐릭터 전신 동작 제어[5] 등에서 효과적인 성능을 보여주었다. 심층 강화학습은 기존 제어 기법에서 다루기 어려웠던 동작을 실시간에 안정적으로 수행할 수 있는 제어기를 생성하지만, 일반적으로 전처리 단계에서 최적의 제어기를 탐색하는데 상당한 계산 시간이 소요된다. 이와는 다르게, 본 논문에서는 확률적 모델예측제어를 통해 최적 제어 정책에 대한 샘플들을 생성하고 이에 기반한 단 한 번의 지도학습으로 제어기를 학습하기 때문에 그 계산 시간을 효과적으로 줄일 수 있다.
Holden과 그의 동료들은 동작 데이터를 다루는 학습 데이터에 노이즈를 추가하여 인공 신경망의 성능을 향상시키는 방법을 제안했다[23]. 이 기법을 통해 모션 캡쳐 후 노이즈를 제거하기 위한 후처리 작업을 자동화할 수 있음을 보여주었다. 본 논문도 이와 비슷하게 모델예측제어 기법을 통해 계산된 최적 제어 정책의 제어 데이터에 노이즈를 추가하여 캐릭터가 최적 제어 정책 근처에서의 다양한 상황을 고려할 수 있게 해주는 학습 데이터를 생성한다.
3. 시스템 개요
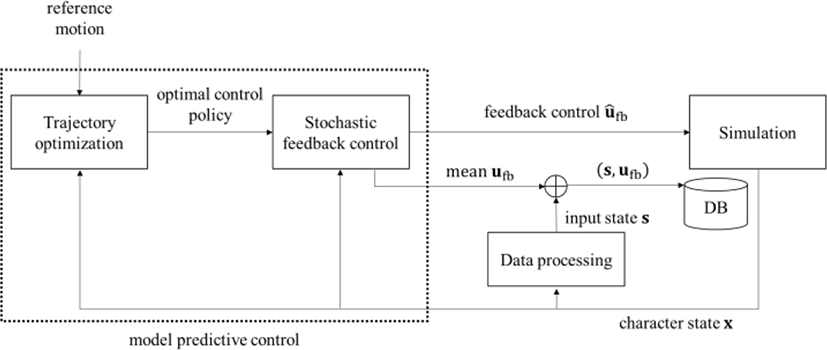
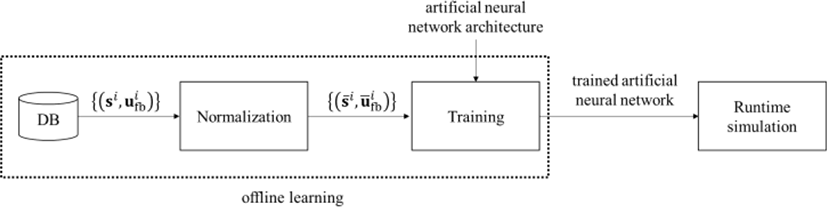
학습 데이터를 생성하기 위해 본 논문에서 제안하는 프레임워크는 크게 학습 데이터 생성 컴포넌트(Figure 1)와 오프라인 학습 컴포넌트(Figure 2)로 구성된다.
참조 동작과 함께 시뮬레이터로부터 캐릭터의 현재 상태 x가 주어지면 첫번째 컴포넌트의 모델예측제어 모듈은 현재 상태 x로부터 시작하여 짧은 시간 윈도우 구간에 대해 참조 동작을 추적하기 위한 최적 제어 정책을 궤적 최적화(trajectory optimization)를 통해 생성한다. 이렇게 생성된 최적 제어 정책은 다시 x와 함께 확률적 피드백 제어 모듈에 전달되어 입력된 x에 대한 최적 제어 피드백 ufb을 평균으로 하는 다변량 정규분포를 통해 노이즈가 포함된 제어 피드백 ûfb을 생성한다. 이렇게 생성된 제어 피드백 ûfb은 시뮬레이터에 전달되어 캐릭터의 현재 상태를 다음 상태로 업데이트 하는데 사용된다. 한편, 캐릭터의 현태 상태 x는 데이터 처리 모듈을 통해 인공 신경망의 입력 상태 s로 변환되고 다변량 정규분포의 평균으로 사용된 최적 제어 피드백 ufb와 함께 학습 데이터를 보관하는 데이터 베이스에 저장된다. 여기서, 최적 제어 피드백 ufb에 노이즈를 포함시킨 제어 피드백 ûfb은 ufb에 비해 캐릭터가 참조 동작을 안정적으로 추적하는 것을 오히려 어렵게 만들지만, 참조 동작 근처의 다양한 상태에 대한 탐색을 가능하게 함으로써 인공 신경망이 과적합(overfitting) 되는 것을 방지하고 외력 등에 캐릭터가 좀더 강인하게 반응하게 하는 학습 데이터를 생성할 수 있게 해준다.
일단, 학습 데이터가 충분히 생성되면, 두번째 컴포넌트는 먼저 그 학습 데이터 를 정규화 시켜서 캐릭터 동작 데이터에 포함된 크기나 단위 차이의 영향력을 제거한다. 그리고 그렇게 처리된 데이터 를 가지고 인공 신경망을 학습하여 제어기를 생성한다.
학습된 제어기는 최종적으로 실행시간 시뮬레이션에 적용되어 모델예측제어 없이도 현재 캐릭터 상태에 대한 실시간 피드백 제어를 수행한다.
4. 학습 데이터 생성
캐릭터의 상태 벡터 x ∈ ℝn는 캐릭터 루트의 위치 및 각 관절의 각도 그리고 이들에 대한 속도 정보로 구성된다. 제어 벡터 u ∈ ℝm는 내부 관절 토크(internal joint torques)만으로 구성된다. 시간 스텝 i에서 제어 벡터 ui와 상태 벡터 xi가 주어졌을 때, 다음 상태 xi+1를 구하기 위한 시스템 동역학 xi+1=f(xi,ui)은 완화된 접촉 동역학(smoothed contact dynamics)에 기반하여 정형화한다(자세한 수식에 대해서는 기존 연구[6,9] 참조). 이 동역학은 강체 충돌을 부드럽게 완화시킴으로써 시스템 동역학을 미분 가능하게 만든다. 이러한 미분 가능성을 이용하여 본 논문에서는 미분 정보를 사용하는 효율적인 궤적 최적화를 통해 최적 제어 정책을 구한다[6,9].
예측 구간의 길이가 N 시간 스텝이고 캐릭터의 현재 상태 x와 참조 동작 이 주어졌을 때, 궤적 최적화 문제는 각 시간 스텝 i=1,…,N에 대한 비용함수 c(xi,ui)와 마지막 시간 스텝에 대한 비용 함수 cf(xN)의 합으로 다음과 같이 정형화 된다.
비용함수의 구성은 기존 연구[6]에 따라 참조 동작을 강인하게 추적하기 위해 아래와 같이 구성한다.
여기서 처음 두 항은 참조 동작과 시뮬레이션 되는 동작 사이의 차이를 최소화 시키기 위한 것으로, 첫번째 항은 두 동작 사이의 캐릭터 상태에 대한 차이를 최소화 시킴으로써 캐릭터의 전반적인 동작이 참조 동작을 따라가도록 하고 두번째 항은 루트에서 머리까지의 벡터 r에 대한 차이를 최소화 시킴으로써 캐릭터 상체의 전반적인 회전 상태가 참조 동작의 상체 회전 상태를 따라가도록 한다. 마지막 항은 동작을 제어하는데 소요되는 제어 에너지를 최소화시키기 위한 것이다.
최적성의 원칙(optimality principle)에 따라 모든 비용의 최적의 합은 다음과 같이 정의되는 최적 값 함수(optimal value function)를 통해 재귀적으로 나타낼 수 있다[6,9,19].
위의 재귀적 함수 정의를 통해 모든 제어 벡터 u1,u2,…,uN-1를 한 번에 같이 고려해야 하는 궤적 최적화 문제를 하나의 제어 벡터 ui만을 구하는 일련의 작은 문제로 분할하여 풀 수 있다. 본 논문에서는 이러한 최적 값 함수를 반복적으로 풀어서 최적 제어 정책을 구하는 DDP의 변종인 iLQG (iterative Linear Quadratic Gaussian)[9]를 사용하여 궤적 최적화 문제를 해결한다. iLQG는 비용함수의 1, 2차 미분 정보와 시스템 동역학의 1차 미분 정보를 이용하여 최적 제어 벡터 시퀀스 {u*i|i=1,2,…,N−1}, 최적 상태 벡터 시퀀스 {x*i|i=1,2,…,N}, 그리고 최적 피드백 이득(gain) 행렬 시퀀스 {K*i|i=1,2,…,N−1}로 구성된 최적 제어 정책을 계산한다. 일단 최적 제어 정책이 계산되면, 시간 스텝 i 에서의 캐릭터 상태 x에 대한 최적 피드백 제어 벡터는 다음과 계산된다.
위에서 두번째 항은 캐릭터의 상태가 최적 상태로부터 벗어난 경우 이를 극복하기 위한 추가적인 제어 입력을 생성하는 역할을 한다.
본 논문에서는 학습 데이터를 수집할 때 캐릭터의 현재 상태가 시뮬레이션을 통해 업데이트 됨에 따라 예측 구간이 그 업데이트 된 캐릭터 상태로부터 시작하도록 예측 구간을 시간 축을 따라 이동시키며 궤적 최적화를 반복적으로 수행한다. 이러한 반복적인 궤적 최적화는 최적 제어 정책을 주기적으로 업데이트 함으로써 최적 제어 정책이 캐릭터의 현재 상태를 효과적으로 반영할 수 있게 해주어 학습 데이터 수집 과정 동안 노이즈가 추가된 제어 피드백으로 인해 약화된 동작 제어의 안정성을 효과적으로 보완해줄 수 있다.
학습 데이터를 수집하는 과정에서 모델예측제어를 통해 계산되는 최적 제어 정책을 가지고 캐릭터 동작이 아무 외란 없이 제어된다면, 단지 캐릭터에 대한 최적 상태와 최적 제어 정보만이 수집되어 제어기 학습에 대해 과적합(overfitting) 문제가 발생할 수 있다. 이 경우 캐릭터 상태의 작은 변화에도 제어기가 강인하게 반응할 수 없게 된다. 이러한 과적합 문제를 다루기 위해, 모델예측제어에 기반한 기존의 학습 기법[20]에서는 다음과 같이 피드백 제어를 다변량 정규분포를 사용하여 확률적으로 정형화 하였다.
여기서 정규 분포의 평균 μ(x)은 기존의 결정론적(deterministic) 최적 피드백 제어 벡터 ufb, 즉, u*i + K*i(x−x*i)로 설정되고 공분산에 사용된 는 iLQG의 문제 해결 과정에서 도출되는 부산물로서 다음과 같이 정의된다.
여기서 (·)는 비용함수의 u에 대한 2차 미분이고, fu(·)는 시스템 동역학의 u에 대한 1차 미분이며, (·)는 최적 값 함수의 x에 대한 2차 미분이다. 를 공분산으로 사용하는 것에 대한 직관적인 의미는 비용에 영향을 많이 주는 제어 입력에는 적은 노이즈를 추가하고 비용에 영향을 적게 주는 제어 입력에는 상대적으로 많은 노이즈를 추가하여 비용적인 측면에서 노이즈 추가에 대해서도 제어기의 성능이 크게 손실되지 않도록 하는 것이다. 하지만 본 논문에서 실험해본 결과 를 아무 변경 없이 그대로 사용하여 노이즈를 추가하는 경우, 의 대부분의 수치 값이 매우 작기 때문에 상당히 큰 노이즈가 매 프레임마다 제어 입력에 추가되어 매우 불안정한 캐릭터 동작을 생성하였고 시뮬레이션이 수치적으로 금방 불안정 해져서 학습에 유용한 데이터를 수집하기가 어려웠다. 이러한 데이터로는 안정적으로 동작하는 제어기를 얻기 어렵기 때문에, Levine과 그의 동료들은 수집된 데이터로 초기 제어기를 학습하고 다시 추가적인 제어 정책 탐색 과정을 통해 제어기를 개선시키는 방식을 취하였다[20].
본 논문에서는 이렇게 기존 방식에서 만으로 안정적인 학습 데이터를 얻기 어려운 문제를 해결하기 위하여 다음과 같이 노이즈의 크기를 제어할 수 있는 사용자 파라미터 δ를 추가한 확률적 피드백 제어를 제안한다.
여기서 δ는 의 대각 성분에 더해져서 제어 벡터에 더해지는 노이즈의 크기를 조절할 수 있을 뿐만 아니라 의 역행렬을 구하는데 수치적 안정성을 제공해줄 수 있다. δ에 대해 작은 값을 줄수록 공분산이 커져서 피드백 제어에 더 큰 노이즈가 추가가 되고, δ의 값이 클수록 공분산이 작아져서 피드백 제어가 결정론적 최적 피드백 제어에 가까워지게 된다. 이러한 사용자 파라미터 δ의 추가는 최적 피드백 제어 벡터의 각 원소에 적당한 크기의 노이즈를 추가함으로써 최적 제어 정책의 주변을 안정적으로 탐색하도록 하여 학습 데이터를 효과적으로 수집할 수 있게 한다. 본 논문에서는 모든 실험에서 δ에 대해 0.0005 을 사용하였다.
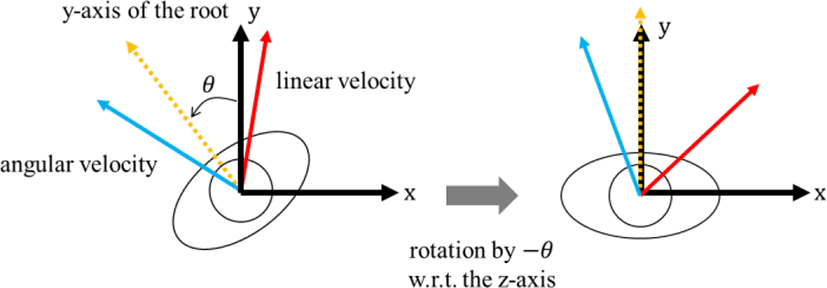
학습 데이터를 수집하기 위해 모델예측제어를 통해 주기적으로 최적 제어 정책을 업데이트하면서 매 프레임마다 현재 캐릭터 상태 x에 대한 최적 피드백 제어 벡터 ufb를 계산한다. 제어 피드백 ufb의 모든 원소는 각 관절의 지역 좌표계에서 정의된 반면, 캐릭터 상태 x에는 원소에 따라 전역 좌표계에서의 위치와 이동 방향도 포함하고 있기 때문에 캐릭터 상태 x를 그대로 사용하는 경우, 학습된 제어기가 특정 전역 위치와 전역 이동 방향에 종속되게 된다. 따라서 본 논문에서는 기존 연구[1]에서 제안한 방법에 따라 변환 함수 g(x)를 통해 x를 이러한 전역 정보에 독립적인 상태 벡터 s=g(x)로 변환한다. 여기서 g(x)는 z축이 up vector 방향을 나타내는 좌표계에서 캐릭터 루트의 xy 평면 상에서의 위치, 곧, 루트의 x, y 좌표를 제거하고 캐릭터의 이동 방향을 나타내는 루트의 y축 방향과 전역 좌표계의 y축 사이의 각 θ만큼 z축을 기준으로 루트의 방위와 선속도, 각속도를 역으로 회전시킴으로서 s를 생성한다 (Figure 3).
g(x)는 또한 캐릭터 동작 흐름에 대한 좀더 명확한 인식을 위해 기존 연구[24]에서 제안한 방법에 따라 cosine 함수 값으로 표현된 캐릭터 동작의 현재 위상(phase)를 s에 추가한다. 이에 따라 s는 총 n–1차원의 벡터로 구성된다(n(x의 차원) – 2(루트의 x, y좌표) + 1(위상)). 매 프레임마다 이렇게 생성된 (s,ufb) 데이터 쌍을 학습 데이터로서 누적한다.
데이터 수집 과정에서 캐릭터의 상태를 업데이트 할 때는 본 논문에서 제안한 확률적 제어를 통해 현재 상태 x에 대한 노이즈를 포함한 피드백 제어 벡터를 계산하고 그 제어 벡터를 통해 시뮬레이션을 진행하여 캐릭터의 상태를 업데이트 한다.
5. 인공 신경망 학습
캐릭터의 상태 벡터나 제어 벡터는 각 원소가 나타내는 관절에 따라 그 크기 및 단위가 상당히 다르기 때문에 그 데이터를 그대로 사용할 경우 학습의 속도나 성능에 많은 영향을 줄 수 있다. 이에 따라 본 논문에서는 학습 데이터의 스케일을 조절하기 위해 z-score 정규화 기법을 이용하여 상태 벡터 s의 각 원소 si,i=1,2,…,n-1와 제어 벡터 u의 각 원소 uj,j=1,2,…,m에 대하여 다음과 같이 정규화를 수행한다.
여기서, 와 는 각각 학습 데이터로부터 계산된 상태 벡터의 i 번째 원소와 제어 벡터의 j 번째 원소의 표본 평균을 나타내고, 와 는 해당 원소들에 대한 표본 표준편차를 나타낸다. 이렇게 정규화된 상태벡터 와 제어 벡터 는 각각 인공 신경망으로 표현되는 제어기의 입력과 출력에 대한 학습 데이터로 사용된다.
제어기를 학습하는데 사용한 인공 신경망은 Peng과 그의 동료들이 제안한 이족 캐릭터 제어기 구조를 참조하여[1], 아래 그림과 같이 3개의 계층으로 구성된다 (Figure 4).
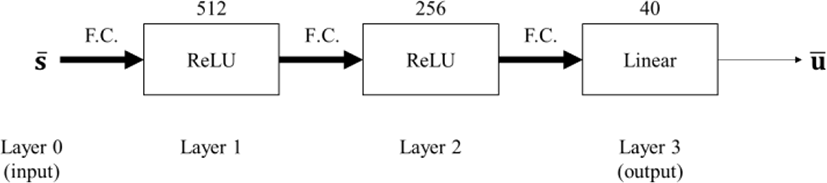
여기서 입력 계층(Layer 0)은 캐릭터 상태 벡터 를 나타내고 두 은닉층(Layer 1과 Layer 2)은 각각 512개와 256개의 ReLU 활성 함수(activation function)로 구성된다. 출력층(Layer 3)은 제어 벡터의 차원 수(m=40)만큼의 선형 활성 함수들로 구성되고 그 함수들의 출력은 정규화 된 제어 벡터 를 나타낸다.
일단 학습이 완료되면, 실행시간 시뮬레이션에서는 캐릭터의 현재 상태 x를 s=g(x)로 변환한 후에 이를 정규화 하여 제어기의 입력으로 사용하고 그에 상응하는 제어기의 출력 은 역정규화를 통해 본래의 제어 벡터 스케일을 복구하여 캐릭터의 제어 입력 u로 사용한다.
6. 실험 결과
본 논문에서 제안한 학습 프레임워크의 효용성을 검증하기 위해 걷기 동작과 달리기 동작에 대한 제어기 학습을 수행하였다. 각 동작에 대해 먼저 확률적 모델예측제어를 통해 학습 데이터를 수집하였고, 그 수집된 데이터를 기반으로 제어기를 생성하였다. 학습 데이터 수집 및 제어기 학습을 수행하는데 걷기 동작의 경우 총 1.5시간 미만의 시간이 소요되었고 달리기 동작의 경우 총 50분 미만의 시간이 소요되었다. 끝으로, 학습된 제어기를 실행시간 시뮬레이션에 적용하여 그 성능과 제어 안정성을 살펴보았다.
실험에 사용된 캐릭터 모델은 6 자유도를 갖는 루트 관절 외에 팔꿈치와 무릎 관절은 hinge 관절로 모델링 되었고, 그 나머지에 해당하는 목, 어깨, 손목, 허리, 고관절, 발목은 각각 3자유도를 갖는 ball 관절로 모델링 되어 총 40 자유도를 갖는다. 인공 신경망을 구축하고 학습시키기 위해 Google Brain에서 개발한 TensorFlow 라이브러리를 사용하였다[25]. 인공 신경망을 학습하는데 MSE (Mean Squared Error)를 손실 함수로 사용했으며, 이를 최적화하는데 Adam 알고리즘을 적용하였다. 이 알고리즘의 학습률(learning rate)은 0.001로 설정하였으며, 1차, 2차 모멘트에 대한 지수적 감쇠율(decay rate) β1과 β2는 각각 0.9와 0.999로 설정하였다. 걷기 동작과 달리기 동작 모두에서 학습을 위해 수행된 epoch의 회수는 300회였으며 batch 크기는 32로 설정하였다. 모든 실험은 Intel(R) Core™ i7-5930K CPU (3.5 GHz, 6 cores), 24GB RAM 및 TITAN X (Pascal) 그래픽카드(3584 GPU cores)로 구성된 컴퓨터에서 진행하였다.
걷기 동작을 학습하기 위해 모델예측제어를 통해 5만개의 (s,ufb) 데이터 쌍을 생성하였으며 이를 위해 약 1시간 11분이 소요되었다. 이렇게 수집된 학습 데이터의 80%(4만개)를 학습에 사용하였고, 나머지 20%(1만개)를 검증하는데 사용하였다. 제어기를 학습하는데 629초(약 10분)의 시간이 소요되었다. 학습과 검증에서의 MSE와 MAE (Mean Abs Error)는 아래 표와 같다(Figure 6).
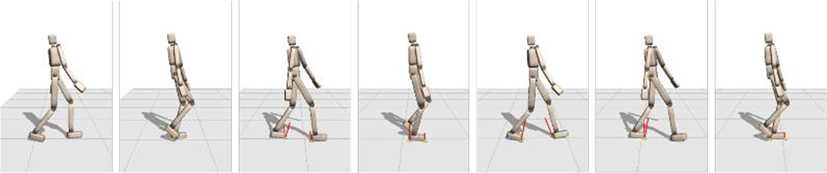
학습된 제어기는 실행시간 시뮬레이션에서 안정적인 제어 성능을 보여주었고(Figure 5), 약간의 외력에도 균형을 잃지 않고 보행 동작을 안정적으로 수행하였다. 이것은 제안된 확률적 제어를 통해 다양한 학습 데이터가 효과적으로 수집된 것을 보여준다.
한편, 동일한 실험 환경 설정에서, 학습데이터에 대한 정규화 없이 제어기를 학습하는 경우, 캐릭터가 두 세 걸음정도 걸은 후에 균형을 잃었다. 이를 통해 데이터 정규화가 효과적인 제어기 학습에 있어서 중요함을 알 수 있다.
또한, 걷기 동작의 경우 학습 데이터를 절반 적은 2.5만개를 사용하여 제어기를 생성한 경우 몇 걸음을 걷다가 결국 균형을 잃은 반면, 달리기 동작의 경우 같은 크기의 학습 데이터로 안정적인 제어기를 학습할 수 있었다(6.3절 참조). 이를 통해 안정적인 제어기를 얻기 위한 학습 데이터의 최소 크기는 동작의 유형에 따라 다르다는 것을 알 수 있다.
일반적으로 달리기 동작은 걷기 동작에 비해 큰 운동량을 가지고 이동하면서 발 내딛는 위치를 신속하게 변경할 수 있기 때문에 큰 외란에도 자세에 대한 흐트러짐 없이 균형을 유지하는데 더 유리하다. 이러한 직관에 따라 달리기 동작의 경우 걷기 동작보다 절반 적은 2.5만개의 (s,ufb) 데이터 쌍을 약 37분 동안 생성하여 제어기 학습을 수행하였다. 걷기 동작과 마찬가지로 수집된 데이터의 80% (2만개)를 학습에 사용하였고, 20%(5천개)를 학습된 제어기를 검증하는데 사용하였다. 제어기를 학습하는데 324초(약 5.4분)의 시간이 소요되었다. 학습 결과에 대한 MSE와 MAE는 아래와 같다(Figure 8).
달리기 동작에 대해 학습된 제어기는 안정적으로 보행 동작을 수행하였다(Figure 7). 또한, 달리기 동작의 내제된 보행 안정성 때문에 걷기 동작에 비해 좀더 큰 외력에도 균형을 안정적으로 유지하였다.
7. 결론
본 논문에서는 확률적 모델예측제어 기법을 통해 간편하면서도 효과적으로 학습 데이터를 수집하는 방법을 제안하였고 이렇게 수집된 데이터를 정규화와 간단한 인공 신경망 구조를 통해 효과적으로 학습할 수 있는 지도학습 기법을 제안하였다. 제안된 프레임워크를 통해 걷기와 달리기 동작에 대해 학습된 제어기를 각각 1-2시간 안에 빠르게 생성할 수 있었다.
한편, 본 프레임워크는 기존의 지도 학습기법과 마찬가지로 제어기의 성능이 학습 데이터의 범위에 제한되는 제약사항을 갖는다. 온라인으로 최적 제어 정책을 실행시간에 주기적으로 업데이트 하는 모델예측제어와 비교하여, 제안된 제어 기법은 학습 데이터 범위 내에서만 캐릭터의 동작을 제어할 수 있기 때문에 다양한 범위에 대해서는 적절한 제어 입력을 생성하지 못하는 한계가 있었다. 이에 따라 현재의 학습 데이터 만으로는 큰 외력에 대해서 충분히 안정적으로 반응하지는 못하였다. 이러한 문제는 외력과 함께 확률적 모델예측제어를 고려하여 학습 데이터를 생성하는 방법으로 접근할 수 있을 것이다.
본 논문에서 제안한 프레임워크를 활용하여, 다양한 유형의 동작들에 대한 물리 기반 캐릭터의 학습 데이터를 생성하고 여러 환경 변화와 사용자 입력에 대해 이러한 동작 사이를 적절하게 이동할 수 있는 제어기를 빠르게 생성하는 물리 기반 애니메이션 기술을 개발하는 것도 흥미로운 향후 연구 방향이 될 것이다.