1. 서론
컴퓨터 그래픽스, 특히 컴퓨터 비전 및 애니메이션 분야에서 사용 되는 3D 모델은 메쉬(mesh)로 이루어져 있다. 모델의 동작(motion)이나 외부 영향에 의해 모델의 모양이 변형(deformation)되 면 영향을 받는 모든 메쉬에 변화가 일어나는데, 이는 상당한 계 산량을 요구한다.
본 연구는 골격(skeletons)이 있고 삼각형 메쉬(triangular meshes)로 이루어진 3D 모델의 변형을 빠른 연산 속도로 구현 하는 것을 목표로 한다. 이를 위해 삼각형 메쉬 정점의 위치를 빠른 속도로 계산할 수 있는 역기구학(inverse kinematics, IK) 풀 이 방법을 연구하고 해당 인터페이스를 개발하였다. 모델 표면상 에 한 개 이상의 마커(markers)를 지정하고 마커의 목표 위치를 설정하면, 이 시스템은 마커의 목표 위치를 기준으로 가속화된 IK 풀이를 통해 모델 표면을 구성하는 삼각형 메쉬 정점의 위치 를 계산한다(Figure 1 참조). 메쉬의 위치를 결정하는 데에는 각 마커와 해당 마커에 영향을 미치는 관절(joints), 그리고 해당 관 절의 상위(부모) 관절에 대하여연산을 수행하는데, 이 과정에서 빈번하게 사용되는 중복된 항(terms)이 발생한다. 이러한 중복항 을 사전에 계산해 둠으로써 비교적 빠른 속도로 메쉬 위치 계산을 진행하며, 모델의 변형된 모습을 신속하게 결과 화면으로 확인할 수 있다.
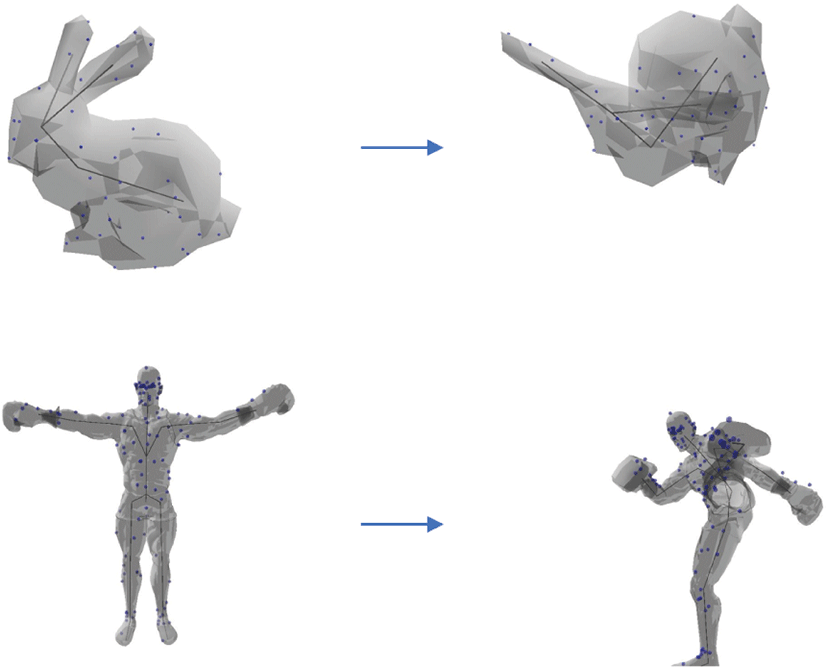
본 연구는 3D 모델 변형에 필요한 IK 풀이를 가속화된 방법으 로 연산 속도를 개선했다는 데에 의의가 있다. 기존의 삼중 중첩 반복(3-nested loop) 구조의 계산 절차와 달리, 중복항을 사전에 계산함으로써 이중중첩 반복(2-nested loop) 구조의 계산 절차를 수행한다. 이러한 개선된 계산 구조를 통해 5장에서 후술할 내용 과같이 모델 변형 결과를 빠르게 구현할 수 있다.
본 연구에서 제안하는 가속화된 IK 풀이 방법은 3D 모델을 다 루는 다양한 분야에서 활용할 수 있다. 예를 들어, 선형 블랜드 스키닝(linear blend skinning, LBS) 기법으로 구현된 3D 모델을 다루는 데 자연스럽고 빠른 속도의 모델 변형 또는 제어(control) 가가능하다. 또한 사용자와의 상호작용 인터페이스를 접목하여 3D 모델의 편집 도구(editing tool)로도 응용할 수 있다. 가속화된 IK 풀이 방법은 컴퓨터 비전 분야에도 적용할 수 있는데, 특히 마커 없이 단순 촬영만으로 대상 물체를 추적하는 무마커 추적 (markerless tracking) 관련 연구에서 유용하게 활용될 수 있다.
본 논문은 총 6장으로 구성되어 있으며, 2장에서는 마커 기반 3D 모델 변형에 관련된 기존 연구를 소개한다. 3장에서는 모델 표면상에 마커를 선택하고 관련 메쉬 정보를 저장하는 과정을 서술하고, 4장에서는 기존의 마커 기반 캐릭터 변형에 사용되는 기존의일반적인 IK 풀이 방법을 소개한다.5장에서는 해당 가속 화된 IK 풀이 방법을 적용한 실험 결과를 그림과 함께 제시하며, 6장에서는 본 연구의 의의와 장단점, 기대효과 등을 서술한다.
2. 관련 연구
이장에서는 본 연구의 주제와 구현 방식이 밀접하게 관련된 기존 연구를 소개한다. 다양한 관련 연구 중에서도, 특히 본 연구에서 3D 모델 변형을 위한 연산 방식으로써 다루었던 IK 풀이 방법 및 이를 이용한 모델 변형 관련 연구를 소개한다. 또한 마커 기반 모델 변형 기술이 유용하게 활용되는 무마커 추적 관련 연구를 소개하며, 해당 연구의 필요성과 활용방안을 제시하고자 한다.
IK는 모델의 자세(모양)를 특징적으로 결정짓는 부분인 엔드 이 펙터(end-effectors)를 목표 위치로 위치시키기 위해 모델의 관절 각도(joint angle)을 계산하는 운동 방정식(kinematic equations)이 다[1]. IK 및 그 풀이 방법을 다루는 연구는 다양한 분야에 널리 수행되어 왔는데, 다양한 야코비 행렬을 이용하여 광범위한 기 술 분야에서 적용되기도 한다[2]. 컴퓨터 그래픽스 분야에서 IK 는 특히 관절 캐릭터(articulated characters)의 동작(자세)을 제어 하는 수단으로 빈번히 채택된다. 또한 관절 캐릭터의 동작 생성 소요시간 단축 및 결과 품질의 향상을위해, 다양한 IK 최적화 풀 이 방법에 관한 연구가 수행되었다[3]. 최근에는 인공지능 기술 의 발전에 발맞추어 데이터 기반(data-driven) 동작 생성 방식과 기계학습(machine learning)을융합함으로써 보다 우수한 품질의 캐릭터 애니메이션 연구가 빈번히 수행되고 있다[4, 5]. IK 풀이 를 효율적으로 수행하기 위한 다양한 접근에 관한 연구는 오늘날 까지도 꾸준히 지속되고 있으며[6], 본 논문에서는 야코비 행렬 (Jacobian matrix)의 계산을 간소화하여 연산 소요시간을 단축하 고자 하였다.
캐릭터 모델, 특히 동작에 따른 모양 변화가 크게 수반되는 연체 캐릭터(soft-bodied characters)와 같은 모델을 제어하는 데 에는 많은 연산량을 수반하는 메쉬 모양 변화를 빠르고 자연스 럽게 적용(update)하는 것 또한 중요하다. LBS 기법은 골격을 가진 모델의 메쉬를 변형하는 가장 대표적인 알고리즘으로, 캐 릭터 관절의 움직임(transformation)에 따라 주변의 다각형 메쉬 (polygon mesh)의 정점 위치를 계산하여 메쉬의 모양을 변형시킨 다[7]. LBS 기법과 IK 풀이를 적용한 캐릭터 모델 변형 관련 연구 는 꾸준히 이루어져 왔다. 메쉬 IK는 예제 메쉬(example meshes) 로부터 유의미한 모양 변화 공간(shape space)을 학습하여 모델 변형 연산을 수행하는 방법이다[8], 앞선 메쉬 IK를 응용하여 일 부 자유도(degree of freedom, DOF)에 대해서만 연산을 진행하 고, 나머지에 대해서는 자동 예측을 통해 모델 변형 연산 속도를 가속화한 시도가 있었다[9], 또한 파충류, 포유류, 곤충, 어류 등 각기 다른 몸체 변형 스타일을 가진 다양한 캐릭터에 두루 적용할 수 있는 빠르고 자연스러운 메쉬 Ik 풀이 방법이 연구하기도 하였다[10]. 이외에도 IK 풀이를 통해 모델 변형의 속도 및 변형 결과 품질 성능을 높이기 위한 연구는 다수 진행되어 왔으며, 본 연구 또한 기존 삼중 중첩 반복 계산 구조의 IK 풀이 방법의 연 산 속도를 가속화하기 위해 계산식 정리를 시도하고 실험을 반 복하였다. 본 연구에서 소개하는 가속화된 IK 풀이 방법은 기존 풀이 연산에서 빈번하게 사용되는 중복항을 사전에 계산함으로 써 삼중 중첩 반복 구조를 이중 중첩 반복 구조로 축약하여 연산 속도를 높였다.
모션 캡처(motion capture, mocap)는 실제 물체나 생물체를 대상 으로 그 움직임이나 변화를 추적하는 것으로, 현실에서의 대상 물체의 움직임을 가상 모델의 데이터 변화 형태로 기록하는 것이다. 가장 일반적인 모션 캡처는 마커 기반 추적(marker-based tracking)으로, 관측 대상에 추적 가능한 소형 기기(마커)를 부착 하여 마커의 위치 변화를 감지 및 기록한다. 이는 마커를 직접 부착하므로 정확도가 일정 수준 보장되지만, 마커를 부착함으로 써 물체의 변화 가능성에 영향을 주어 자연스러운 관측이 어려운 경우도 있으며, 물체의 변화에 따라 마커가가려지거나 관측카메 라 기준으로 마커의위치가 중첩될 경우에는 그 정확성이 떨어질 수도 있다. 또한 마커 부착이 실질적으로 불가능한 물체는 실험 대상으로 취급하기 어렵다는 단점이있다. 무마커 추적은 카메라 에 관측되는단편적인이미지(images)만으로 그 모양을 추적하는 것으로, 마커 기반 추적 기술의 단점을 보완할 수 있는 가능성이 있다[11]. Microsoft사의 Kinect와 Intel사의 RealSense는 대표적 인 무마커 모션 캡처 카메라로, 저가형으로 제작되어 사용자의 자세 및 동작을 추적하여 가벼운 오락 및 체험 컨텐츠를 즐길 수있도록 널리 보급되어 있다[12, 13]. Simi Shape 와 같은 고차원 무마커 모션 캡처 장비 또한 다양한 연구 분야에서 활용되고 있 으며[14], 기계학습을 접목하여 여러 사람들의 신체부위를 실시 간으로 추적하는 OpenPose, DensePose 기술 또한 널리 응용되고 있다[15, 13]. 무마커 추적 기술은 다양한 분야에서 널리 사용되 고 있으며, 그 필요성이 대두됨에 따라 무마커 추적의 정확도 및 속도 성능을 높이기 위한 연구 또한 다양하게 진행되고 있다[16]. 본 연구는 삼각형 폴리곤(polygon)으로 이루어진 3D 메쉬 모델 의 표면상에 마커를 생성하고, 마커의 목표 위치를 기반으로 모 델 변형을 신속하게 연산하고자 한다. 해당 기술을 응용하여 3D 모델의 편집 도구로 활용할 수 있고, 마커 기반 또는 무마커 추적 결과를 빠르게 보정하는 데에 적용할 수 있다.
3. 마커 선택 및 메쉬 정보 저장
이장에서는 삼각형 메쉬로 이루어진 3D 모델의 표면상에 임의의 점을 마커로 선택하고, 마커의 목표 위치를 기반으로 IK 풀이를 수행하기 위해 마커를 포함하는 삼각형 메쉬에 관한 정보를 저장하는 과정을 간략히 소개한다. 본 연구에서는 표면이 삼각형 폴리곤으로 이루어진 3D 모델의 변형을 다루는데, 삼각형은 3D 모델을 구성할 수 있는 가장 단순한 폴리곤으로 모델의 모양 변화가 비교적 자유롭고계산 또한 용이하다.
마커는 사용자의 모델 관측 시점(viewport) 기준으로 가시적인 모델 표면상에 생성하는 것으로, 표면을 구성하는 삼각형 메쉬 내부의 임의의 한 점을 마커로서 선택할 수 있다(Figure 2 참조). 사용자가 한 점을 마커로 선택하기 위해, 관측 시점으로 부터 모 델을 향하는 카메라의 초점에 대한 벡터와 폴리곤의 법선 벡터 (normal vector)의 내적(dot product)을 통해 부호를 비교해서 가 시적인 마커를 포함할 수 있는 폴리곤으로 인식한다. 이 때 마커 를 포함한 삼각형 폴리곤의 세 정점(vertices)의 지역 좌표계(local coordinate) 및 해당 좌표계 기준의 지역 위치(local position), 세 정점의위치가 마커의위치에 미치는 영향력을 반영하는 가중치 (weights)를 저장한다. 저장된 폴리곤 메쉬의 정보는 마커의 목표 위치를 기반으로 IK 풀이 연산을 수행할 때 사용된다.
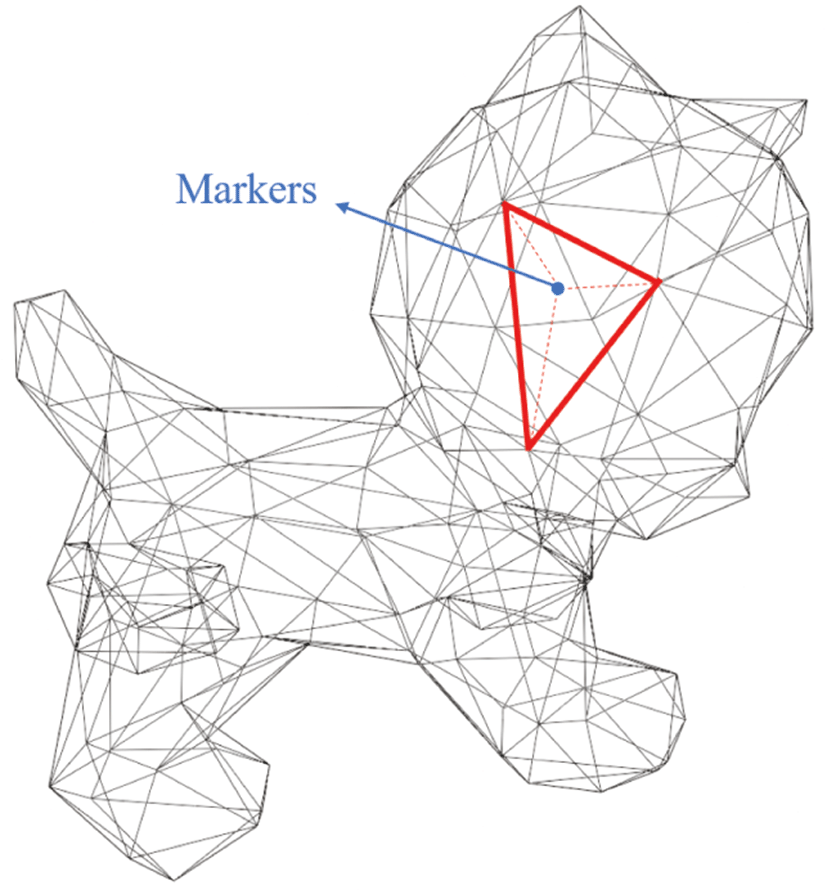
Figure 2는 삼각형 메쉬로 이루어진 모델 표면에 임의의 점을 마커로 선택하고, 해당 마커를 포함하는 삼각형 폴리곤이 결정된 예를 보여준다. 마커는 모델 관측 시점 기준으로 가시적인 표면 메쉬 부분에 생성하며, 각 삼각형 폴리곤마다 한 개의 마커를 생 성할 수 있다. 따라서 사용자의 모델 관측 시점에 따라 가시적인 메쉬가 달라지면서 마커의 생성 가능한 범위 및 최대 개수 또한 달라질 수 있다.
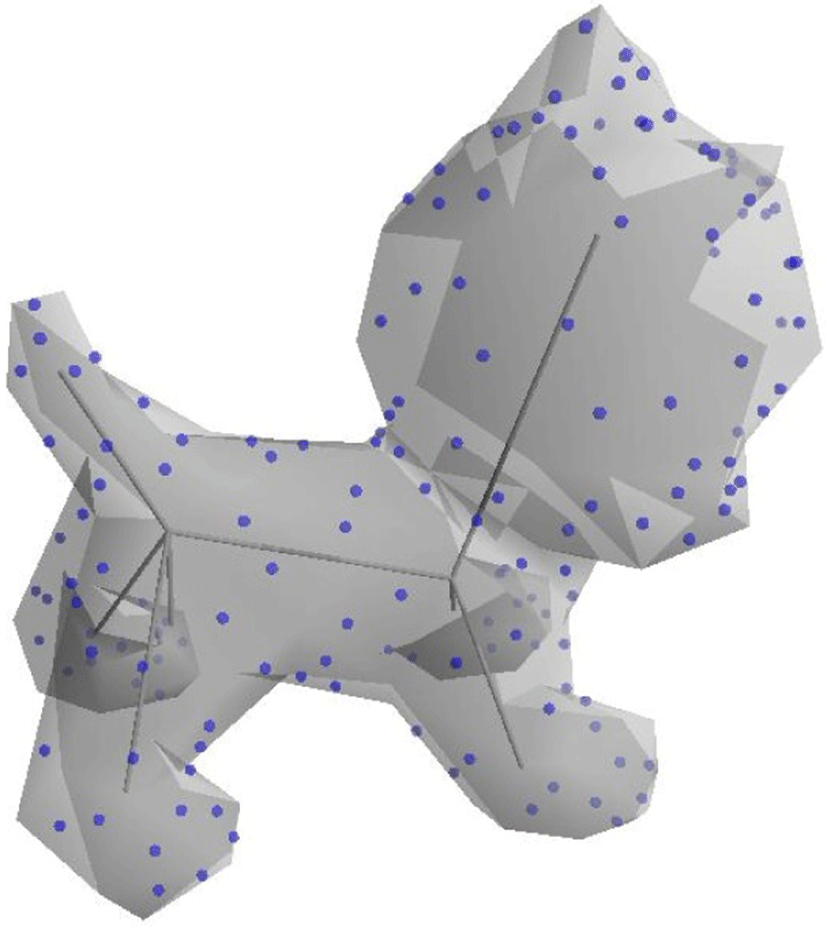
Figure 3은 삼각형 메쉬로 이루어진 고양이 모양의 3D 모델을 사용하여 모델 표면 상에 생성 가능한 모든 마커를 생성한 결과를 보여준다. 관측 시점으로부터 관측되는 모든 표면 폴리곤마다 각 한 개씩의 마커를 생성한 것으로, 모델 변형 기준으로써 그림에 표시된 것과 같이 모든 마커를 사용할 수도 있고 일부 마커만을 선택하여 모델 변형을 구현할 수도 있다. 또한 그림에 제시된 시 점과 달리 사용자의 의도에 맞게 관측 시점을 바꾸어 모델의 다른 신체부위에 마커를 생성할 수도 있다. 마커는 위치 제약조건 (position constraints)의 역할을 하므로 마커의 개수에 따라 모델 변형의 결과가 달라지는데, 마커의 개수가 많아질수록 비교적절 제된 변형이 구현된다(5.1절 참조).
4. 가속화된 IK 풀이
이장에서는 마커의 목표 위치를 기준으로 모델 표면상의 삼각형 메쉬를 변형하기 위해 그 위치를 계산하는 IK 풀이 방법을 소개 한다. 기존의 풀이 방법을 소개하고, 연산 속도의 성능 향상을위 해 기존 방법으로부터 가속화된 IK 풀이 방법을유도하는 과정을 설명한다.
마커의 목표 위치는 모델을 변형하는 데 작용하는 위치 제약조건 의 역할을 한다. 일반적으로 해당 제약조건에 따라 모델을 변형 하려면 목적 함수(objective function)와 그 편미분식(gradient)을 다음과같이 정의한다(수식 1, 2 참조).
수식 1 및 2에서 q는 3D 모델의 특정 자세(모양새)를 가리키며, fk(q)는 현재 자세 q의 표면상에 존재하는 k번째 마커의 목표 위치에 대한 목적 함수이다. 이 때 xk 또는 xk(q)는 k번째 마커의 현재위치, x′k는 목표 위치를 가리킨다. 수식 1의 목적함수는 마커의 현재위치와 목표 위치 간의 오차(difference)를 계산하여 그 값을 최소화하는 방향으로 모델을 변형시키며, 수식 2는 목적 함수를 편미분한 것이다.
k번째 마커의 위치값 xk(q)은 모델 내부에 존재하는 관절 (joints)의 값을 이용하여 다음과 같이 표현할 수 있다(수식 3, 4 참조).
수식 3에서 는 k번째 마커의 위치에 영향을 주는 i번째 관절 기준의 지역 좌표계 상으로 표현된 해당 마커의 위치를 가리키 고, Ti는 관절의 전역 좌표계를 표현하는 행렬, 는 i번째 관 절값이 k번째 마커 위치에 영향을 주는 정도를 나타내는 가중치 를 나타낸다. 이 때 좌표계 Ti는 회전(rotation) 행렬 Ri와 이동 (translation) 요소 pi로 구성되어 있으며(Ti = (Ri, pi)), 따라서 수식 3는 수식 4로 바꾸어 쓸 수 있다.
또한 목적함수의 편미분인 수식 2는 다음과 같이 다시 정리할 수 있다(수식 5 참조).
수식 5에서 Ji는 편의상 기존 수식 2의 을 치환한 것으로, Ji은 3개 행 및 (관절의 수 × 각 관절의 자유도(degree of freedom, DOF))개의 열로 이루어진 야코비 행렬의 형태를 지닌다. 행렬의 각 열(columns)은 관절의 회전축 벡터 a 및 마커의 현재 위치 x 와 관절의 현재 위치 s 간의 오차의 외적, 즉 a × (x − s) 형태로 이루어져 있다. 예를 들어 i번째 관절에 대해서 Ji의 l번째 열은 이다. 여기서 마커 위치 는 다음과 같이 표현할 수 있다(수식 6 참조).
이 때 a, x, s는 모두 전역 좌표계 기준으로 표현된 값으로, 사전에 계산된 값이다.
앞서 제시한 목적 함수 및 편미분을 그대로 연산을 수행하는 것은, 다음과 같은 세 가지 요소에 대하여 동시에 계산하는 것이 다.
-
- 각 마커 k에 대하여
-
- 마커의위치를 정의하는 각 관절 i에 대하여
-
- 해당 관절의 그 부모 관절에 대하여 (Ji의 0이 아닌 컬럼 (non-zero columns)에 대한 연산)
계산식은 삼중 중첩 반복 계산 구조로 구현되는데, 이러한 중첩 반복은 계산량이 방대하여 실제 계산을 수행하는 데 소요시간의 부담이 크다. 다음 절에서는 이러한 목적 함수와 편미분의 연산을 기존의 IK 풀이 방법으로 수행하는 방법을 서술하고, 해당 연산 을 가속화시키는 아이디어를 소개한다.
4.1절에서 정의한 수식을 풀이하는 데 앞서 기존의 목적 함수(수식 1)와 편미분식(수식 5)을 편의상 다음과같이 요약하였다(수식 7, 8 참조).
수식 7에서 ΔSk는 를 축약한 것이고, 수식 8에서 δk는 를 축약한 것이다.
이러한 목적함수와 편미분식의 IK 풀이를 위해서는다양한 방 법이 있는데, 가장 단순한 방법은 수식을 있는 그대로 계산하는 것이다. 편미분식의 경우, 모든 마커에 대하여 계산을 수행할 때 각 마커에 대한 계산값을 순차적으로 더한다(수식 9 참조).
수식 9는 삼중 중첩 반복 구조 내에서 계산되고, 각 마커에 대한 연산을 반복할 때마다 δ·(a × (x − s)) 값을 계산하므로 많은 연산량(소요시간)을 요구한다.
이 절에서는 앞서 서술한 기존의 IK 풀이 연산식을 보다 간략하 게 정리하여 삼중 중첩 반복 구조의 연산 과정을 이중 중첩 반복 구조로 재구성하는 아이디어를 순차적으로 서술한다.
앞선 수식 6에서 마커의 위치를 와 같이 정 의하였고, 야코비 행렬 Ji의 각 열은 c = a × (x − s)의 형태를 지닌다 (수식 9 참조).
수식 10에서 햇(hat, ) 연산자는 두 벡터에 관한 외적식을 행렬 곱으로 표현한다.예를 들어 임의의 벡터 와 에 대하여 가 성립한다. 여기서 햇 변수는 3 × 3 크기의 반대칭 행렬(skew-symmetric matrix)의 형식을 갖추고 있다.
수식 10에서 현재 위치 x에 수식 6을 대입하면, 수식 8의 δkJi은 Ji의 각 열에 대하여 다음과 같은 형태의 연산을 수행한다(수 식 11 참조).
즉, gk(q)을 계산하기 위해서는 각 마커 k와 연관된 i번째 관절, 그리고 야코비 행렬 J의 각 열 l에 대하여 정리된 수식 11을 반 복적으로 계산하여 더한다(Σ). 이러한 삼중 중첩 반복 구조로 이루어진 수식을 쉽게 설명하기 위해 인덱스(index) i와 l은 고정 하고, 마커 인덱스 k에 대한 반복 구조에 대해서만 살펴보도록 한다. 가장 안쪽 반복문이 두 번 실행되는 간단한 경우를 가정하 면, 편미분식 기여분의 합은 다음과같이 표현할 수 있다(수식 12 참조).
수식 12를 일반화하면, 편미분식의 계산 과정은 다음과 같이 같 이 요약할 수 있다(수식 13 참조).
수식 13에서 Ni는 i번째 관절과 연관된 마커들의 인덱스의 집합 이고, 여기서 초록색 밑줄로 표시된 각계수 ∑ δk및 항은 사전에 계산이 가능한 연산 내용이다. 전처리(pre-process) 된 계산 내용을 이용하여 IK 목적 함수의 편미분식을 계산하면, 각 마커에 대한 반복 연산이 불필요하므로 기존의 삼중중첩 루프를 두개의 이중 중첩 반복 계산 구조로 단축하는 것이 가능하다. 첫번째 이중중첩 반복 구조는 k와 i에 대한 이중 반복문으로, 전 처리 항들을 i를 인덱스로 하는 배열에 저장한다. 또 두번째 이중 중첩 반복 구조는 i와 l에 대한 이중 반복문으로, 수식 13에 대한 연산을 수행하는 것에 해당한다.
앞서 4.2절에서소개한 기존의 IK 풀이 방법은 삼중중첩 반복 구조로 연산을 수행하므로 연산량이 방대하고 모델 변형 소요시 간의 부담도 크다. 본 연구는 기존의 IK 풀이 수식들을 정리하여 빈번히 중복되는 항을 발견하고 사전에 계산함으로써, 목적 함수 의 편미분식을 연산하는 과정에서 각 마커에 대한 반복 계산을 줄였다. 결과적으로 전반적인 IK 연산 과정을이중중첩 반복 구 조로 단축함으로써 모델 변형을 신속하게 구현할 수 있었다. 가 속화된 IK 풀이 방법을 통한 모델 변형 결과와 연산 소요시간의 측정 결과는 5장에서 확인할 수 있다.
5. 실험 결과
이 장에서는 본 연구의 3D 모델의 신속한 변형을 위한 가속화 된 IK 풀이 방법의작동을 확인하기 위한 실험내용 및 그 결과를 소개한다. 또한 기존의 삼중 중첩 반복 구조의 계산 방법과 모델 변형 수행 속도를 비교하여 성능을 평가하고자 한다.
실험에는 i7-6700k CPU, 16G RAM, GeForce GTX TITAN X GPU를 장착한 컴퓨터를 사용하였다. 실험에 사용한 삼각형 메 쉬로 이루어진 3D 모델로는 직육면체 스펀지, 이구아나, 고양이, 토끼, 인체 캐릭터 등 다섯 가지를 준비하였다. Table 1은 실험에 사용한 다섯 가지 모델의 구현 정보를 표시한 것으로, 해당 표에 서 Skeletons, Vertices, Meshes 열은 각각 모델이 가진 뼈대의 수, 모델 표면을 구성하는 정점 및 삼각형 폴리곤의 수를 나타낸 것 이다. 또한 Markers 열은 모델의 표면에 적용할 수 있는 마커의 최대 개수로, 실험 당시의 임의의 관측 시점으로부터 생성할 수 있는 마커의 개수를 센 것이다. 삼각형 폴리곤 한 개당 한 개의 마커를 생성할 수 있으므로, 이는 관측 시점 기준으로 가시적인 표면 폴리곤들의 개수라고도 할 수 있다. 이 때 가속화된 IK 풀이 연산 과정에서 발생하는 중복항의 계산은 전처리 과정으로 사전 에 수행되었다.
| Model Type | Skeletons | Vertices | Meshes | MeshesMarkers |
|---|---|---|---|---|
| Cuboid sponge | 6 | 654 | 1040 | 520 |
| Iguana | 18 | 124 | 244 | 136 |
| Cat | 16 | 159 | 314 | 158 |
| Bunny | 8 | 184 | 364 | 163 |
| Human | 26 | 13806 | 12764 | 7526 |
실험에 사용된 각각의 다섯 가지 모델은 300 프레임(frames)에 걸 쳐 특정 동작을 취하는데, 각 프레임별로 동작에 알맞게 변형된 모델의 표면 위치를 마커의 목표 위치로 대응시킨다. 실험 당시 임의의 관측 시점으로부터 생성 가능한 마커들 중에서 임의로 일 부의 마커만을 선택하여(1개,5개, 10개, 50개, 120개) 모델 변형 을 시도하였는데, 이 때 마커의 목표 위치는 모델 변형 과정에서 위치 제약조건의 역할을 수행하는 셈이다. 실험에서는 모델의 동 작과정에서 대응된 마커의 목표 위치를 기준으로, 기본 자세(rest pose)의 모델을 가속화된 IK 풀이 방법을 통해 변형시켰다.
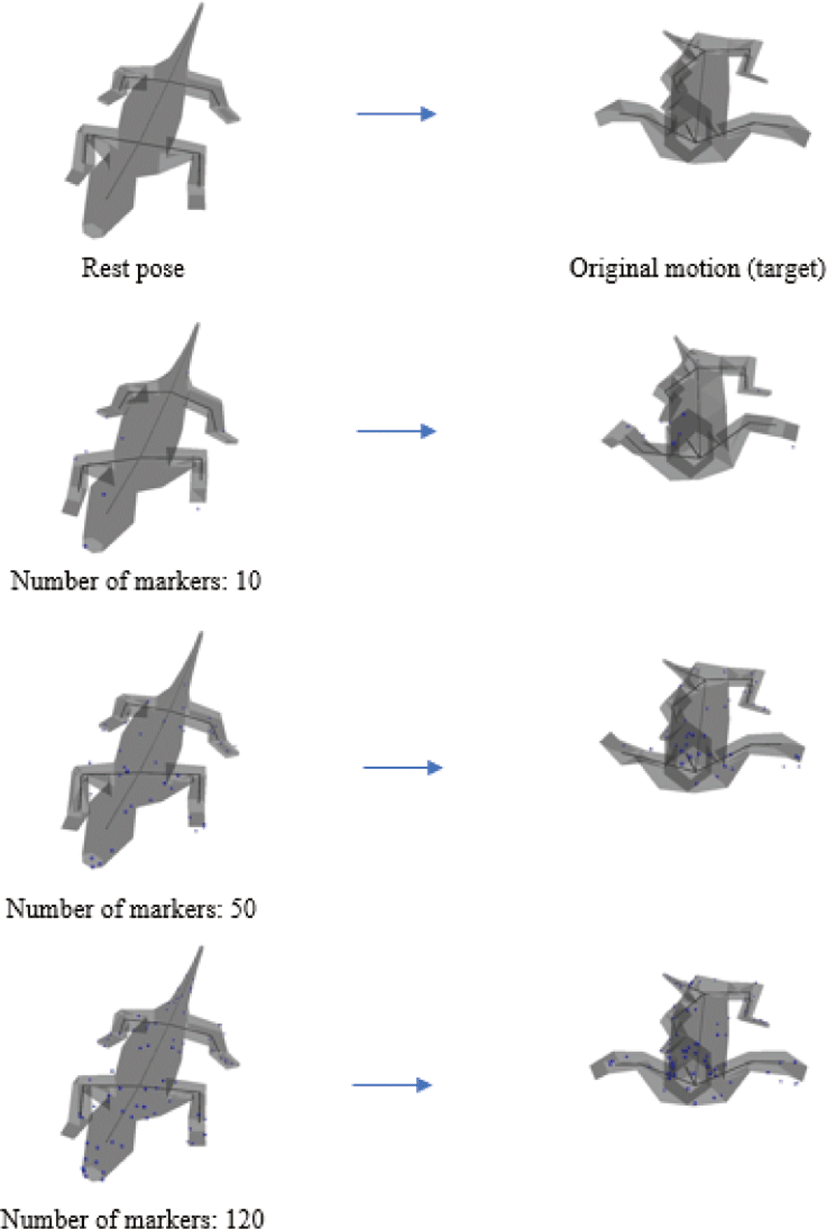
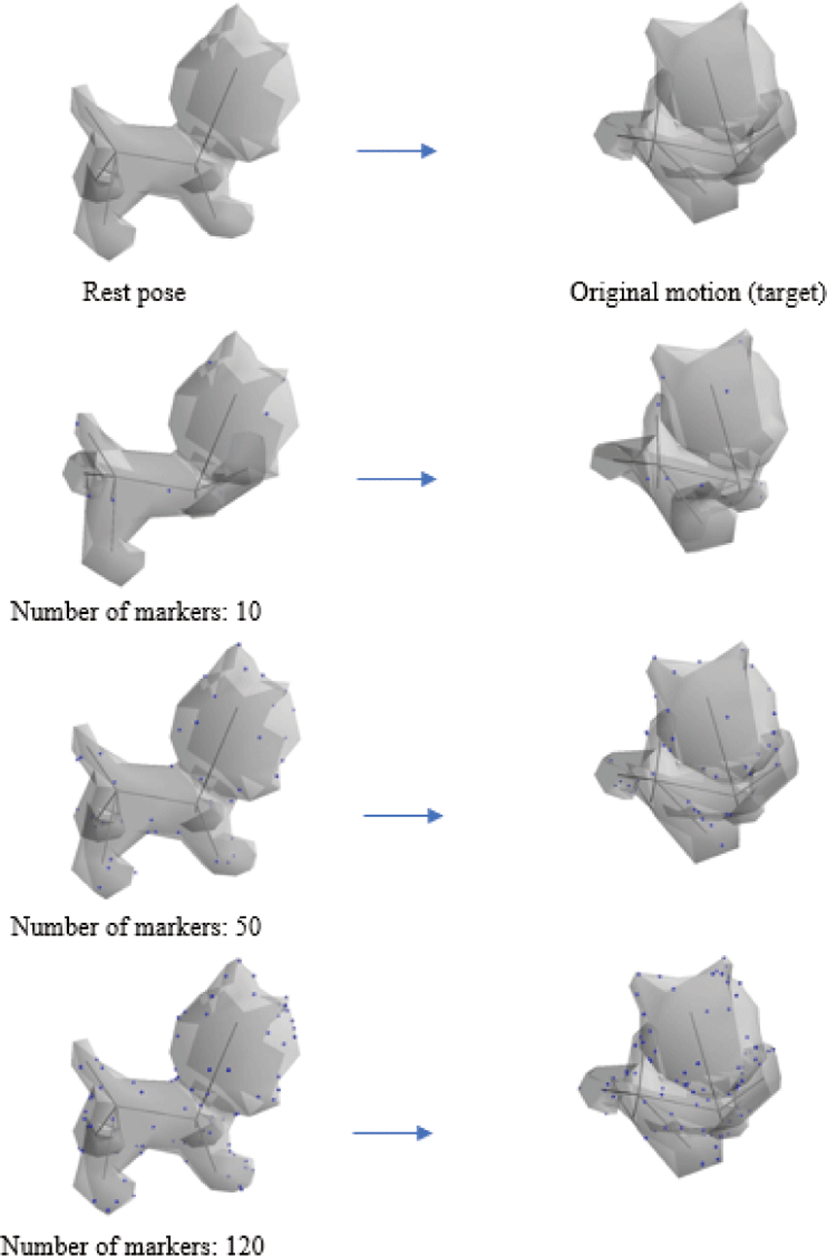
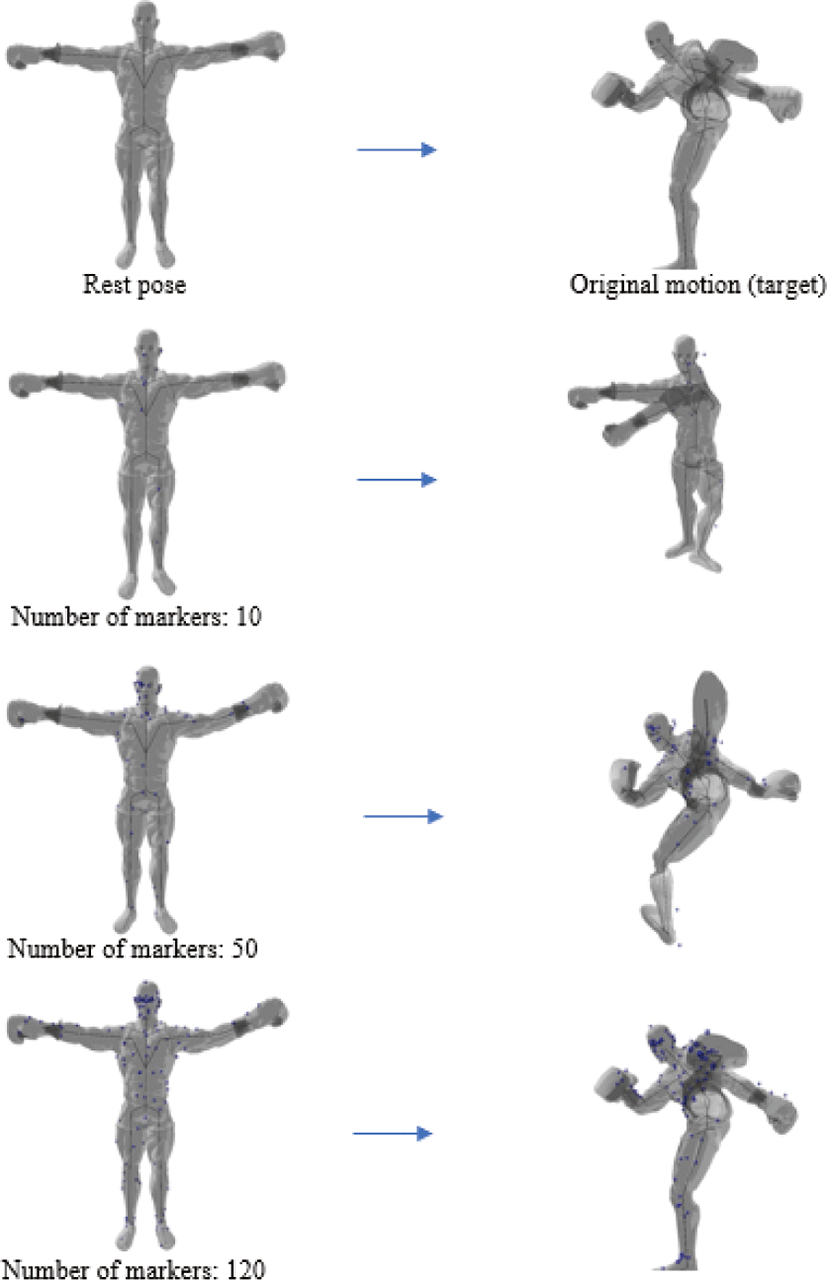
Figure 4-8은 앞서 언급한 다섯 가지 모델의 기본 자세와 특정 동작을 수행한 후 변형된 자세, 모델의 기본 자세에서 임의로 선 택한 마커와 마커의 목표 위치를 기준으로 가속화된 IK 풀이 방 법으로 변형된 결과를 보여준다. 마커의 개수는 위치 제약조건과 비례하므로, 마커의 수가 적을수록 모델의 자유로운 자세 변형 이이루어지고 반대로 마커의 수가 많을수록 절제된 자세 변형이 이루어지는 경향을 확인할 수 있다. 즉, 마커가 적을수록 제약조 건이 적어 모델을 기본 자세로부터 목표 자세로 제어하는 것이 비교적 어렵고, 마커가 많을수록 목표 자세와 가깝게 제어하는 것이 가능하다. 그러나 마커가 1개인 경우에는 해당 마커 이외의 다른 제약조건이 없으므로, 변형 시 모델의 형태 변화보다는 단 순 이동 및 회전이 이루어진다. 또한 마커의 수가 적을수록 메쉬 정점의 위치가 목표 자세와 비교하여 크게 변화하는 대신 삼각 형 메쉬 모양의 변화는 상대적으로 적고, 마커의 수가 많을수록 메쉬 모양이 크게 변화하는 대신 목표 자세와 비교하여 위치가 적게 변화한다. 결론적으로 마커의 수가 많을수록 그 변형 결과 자세가 목표 자세와 비슷해지는 것을 확인할 수 있다.
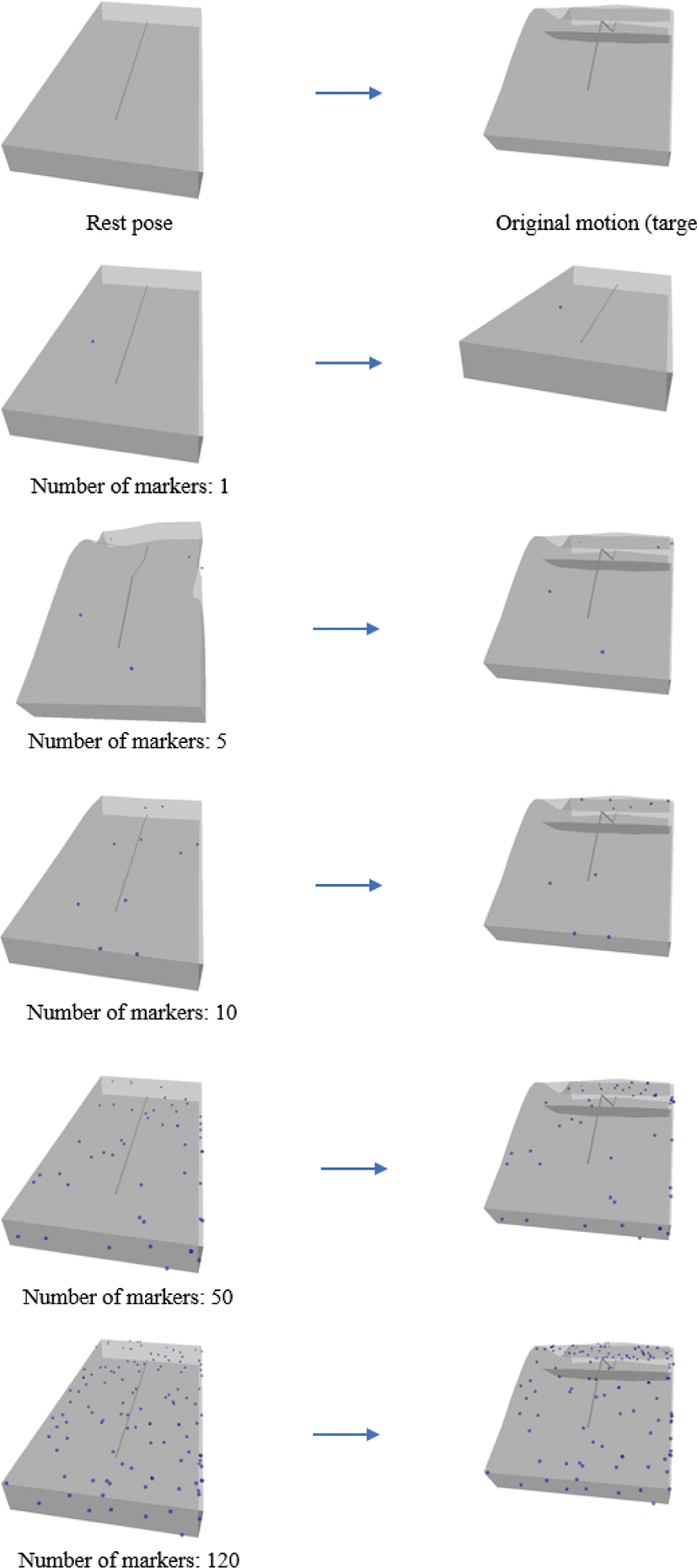
Figure 4는 직육면체 스펀지 모델의 마커의 개수를 변화시키며 모델 변형을 시도한 결과이다. 마커가 1개일 때 변형 결과는 모 델 전체가 단순 이동한 것이나, 마커의 갯수가 증가할수록 변형 결과가 목표 자세와 가까워지는 것을 확인할 수 있다. 직육면체 스펀지 모델의 경우 그 모양새가 매우 단순하여, 마커의 수가 적 은 경우에도 충분히 목표 자세와 유사한 변형 결과를 도출할 수 있다. Figure 5는 이구아나 모델을 실험한 것이다. 마커 개수가 적을 때(5개, 10개), 변형 결과는 목표 자세와 크게 다른 양상을 보이는데, 이는 앞다리 부분에 마커가 설정되지 않아서 위치 제 약조건이 부자연스럽게 적용되었기 때문이라 할 수 있다. 그러나 마커의 개수가 많아질수록, 모델 표면 메쉬에 마커들이 고르게 분포하게 되어 변형 결과가 목표 자세와 유사하게 자연스럽게 연 출되는 것을 확인할 수 있다. Figure 6는 고양이 모델을 실험한 것으로, 이구아나와 마찬가지로 마커의 개수가 적을 때에는다리 부분에 마커가 설정되지 않아서 변형이 부자연스러우나 마커의 개수가 증가할수록 고르게 분포되어 변형 결과가 목표 자세와 유 사해지는 것을 확인할 수 있다. Figure 7는 토끼 모델을 실험한 것 으로, 마찬가지로 마커의 개수가 적을 때에는 귀 부분에 마커가 설정되지 않아서 변형 결과가 목표 자세와 다른 양상을 보인다. Figure 8는 인체 모델을 실험한 것으로, 프레임 증가에 따라 발 차기 동작을 수행한다. 마커가 1개일 때 변형 결과는다른 모델과 마찬가지로 모델 전체가 단순 이동한다. 마커의 개수가 적을 때(5 개, 10개)에는 모델의 복잡한 모양새 대비 마커가 충분히 고르게 분포되지 않아, 팔과 다리 부분의 변형 결과가 목표 자세와 전혀 다른 양상을 보인다. 그러나 충분히 많은 숫자의 마커가 설정되있 을 때에는 변형 결과가 점차적으로 목표 자세와 가까워지는 것을 확인할 수 있다.

본 연구는 3D 모델의 변형을 빠른 연산 속도로 구현하는 것을 목표로 하며, 기존의 삼중 중첩 반복 구조를 개선하여 이중 중첩 반복 계산을 수행함으로써 그 성능을 향상시켰다. 성능 향상의 정 확한 확인을 위하여 모델 변형 실험을 기존의 IK 풀이 방법(삼중 중첩 반복)과 새롭게 제안하는 가속화된 IK 풀이 방법(이중중첩 반복) 두 가지 방식으로 수행하여 그 속도를 비교하였다.
Figure 9은 매 프레임마다 IK 풀이에 소요되는 연산 시간을 그 래프로 작성한 것이다. 해당 실험은 다섯 가지 모델에 120개의 마커를 생성시킨 후에 관측한 것으로, 그래프에서 주황색 선은 기존의 삼중 중첩 반복 구조의 계산 방식에 따른 소요시간을, 파 란색 선은 새롭게 제안하는 이중 중첩 반복 구조의 계산 방식에 따른 소요시간을 표시한 것이다. 그림을 통해 실험에 사용한 모 델과 상관없이 기존 IK 풀이 방법보다 새로운 가속화된 IK 풀이 방법이 빠른 속도로 연산을 수행하는 것을 확인할 수 있다. Figure 9(a)는 직육면체 스펀지 모델을 사용하여 실험을 수행 및 비교한 결과이다. 해당 실험에서 기존 IK 풀이 방법의 경우 전체 프레임 평균 27. 0183ms의 소요시간이 걸리고, 새로운 가속화된 IK 풀이 방법의 경우 평균 7.6984ms의 소요시간이 걸리는데 이는 기존 보다 약 3.50배 빠른 속도이다. Figure 9(b)는 이구아나 모델을 사용하여 실험한 것으로, 기존 IK 풀이 방법의 전체 프레임 평 균 연산 소요시간은 405.4133ms이고, 새로운 가속화된 IK 풀이 방법의 평균 연산 소요시간은 134.1667ms로 기존보다 약 3.02 배 빠른 속도이다. Figure 9(c)는 고양이 모델을 사용하여 실험한 것으로, 기존 IK 풀이 방법의 전체 프레임 평균 연산 소요시간 은 178.8598ms이고, 새로운 가속화된 IK 풀이 방법의 평균 연 산 소요시간은 56.8361ms로 기존보다 약 3.14배 빠른 속도이다. Figure 9(d)는 토끼 모델을 사용하여 실험한 것으로, 기존 IK 풀이 방법의 전체 프레임 평균 연산 소요시간은 86.8782ms이고, 새로 운 가속화된 IK 풀이 방법의 평균 연산 소요시간은 26.6069ms 로 기존보다 약 3.26배 빠른 속도이다. Figure 9(e)는 인체 모델을 사용하여 실험한 것으로, 기존 IK 풀이 방법의 전체 프레임 평균 연산 소요시간은 90.5867ms이고, 새로운 가속화된 IK 풀이 방법 의 평균 연산 소요시간은 32.4783ms로 기존보다 약 2.78배 빠른 속도이다. 이러한 실험을 통해 새롭게 제안하는 이중 중첩 반복 구조의 IK 풀이 방법이 기존의 방법보다 모든 모델 평균 약 3.14 배 빠른 연산 속도로 모델 변형을 구현하는 것을 확인할 수 있다.
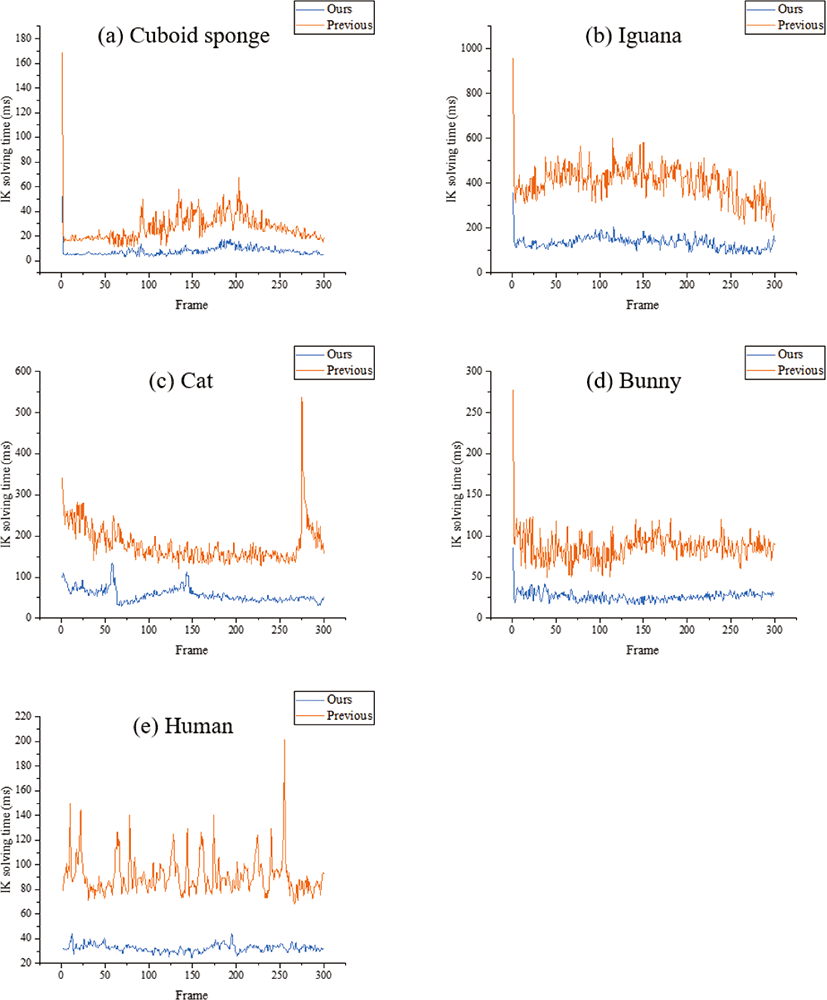
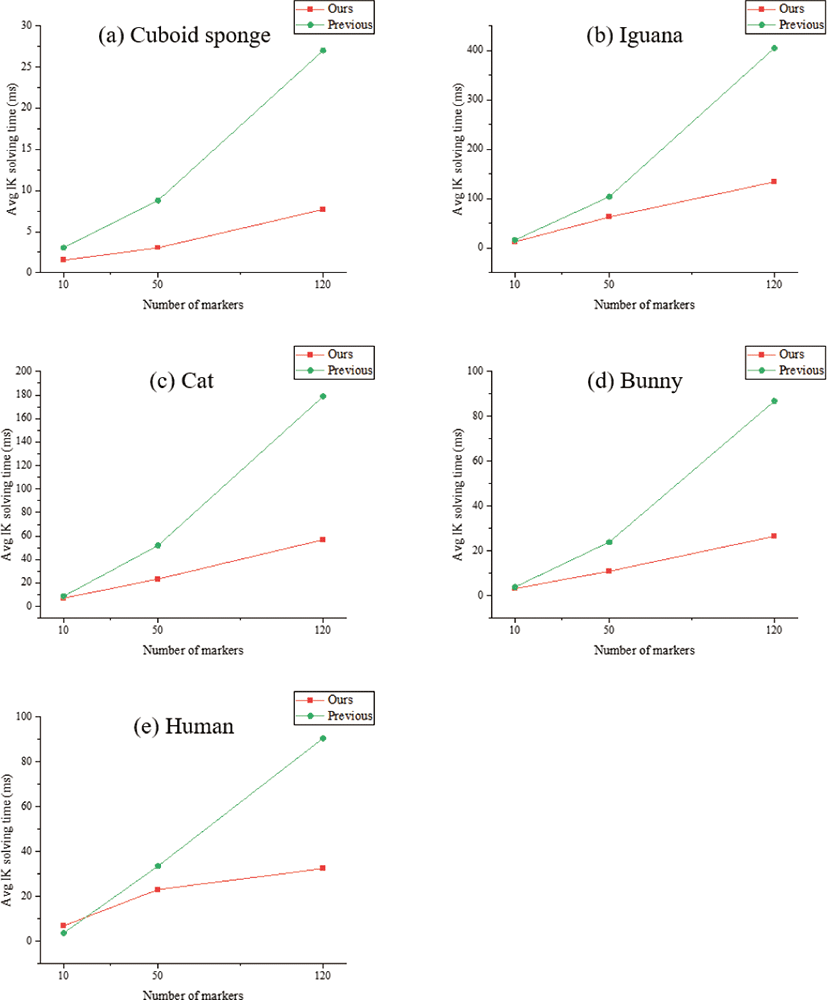
Figure 10은 마커의 개수가 각각 10개, 50개, 120개로 증가함에 따른 전체 프레임의 평균 연산 시간을 그래프로 작성한 것이다. 그래프에서 초록색 선은 기존의 이중 중첩 반복 구조의 계산 방 식에 따른 평균 소요시간을, 빨간색 선은 새롭게 제안하는 삼중 중첩 반복 구조의 계산 방식에 따른 평균 소요시간을 표시한 것 이다. 마커의 개수가 증가할수록 제약조건이 증가하여연산 시간 또한 증가하는데, 해당 실험의 결과 마커 개수가 증가함에 따라 두 IK 풀이 방법의 연산 시간이 증가하는 기울기가 크게 벌어지 는 것을 확인할 수 있다. 인체 모델을 사용한 실험에서 마커가 10 개 생성된 경우, 기존의 IK 풀이 방법(3.7711ms)이 새로운 가속 화된 IK 풀이 방법(6.9772ms)보다 평균 연산 소요시간이 빠른데 이는 3.2061ms 정도의 근소한 차이라고 할 수 있다. 이러한 예 외적인 상황을 제외하면, 전반적으로 새로운 가속화된 IK 풀이 방법이 기존의 IK 풀이 방법보다 연산 속도가 빠른 양상을 보이 며, 마커(제약조건)의 수가 증가할수록 그 성능 향상의 폭이 크게 드러나는 것을 확인할 수 있다.
6. 결론
본 연구는 골격이 있고 삼각형 메쉬로 이루어진 3D 모델의 변 형을 빠른 연산 속도로 구현하는 것을 목표로 한다. 이를 위해 삼각형 메쉬의 위치를 빠른 속도로 계산할 수 있는 IK 풀이 방 법을 연구하였다. 모델 표면상에 한 개 이상의 마커를 지정하고 마커의 목표 위치를 설정하면, 이 시스템은 마커의 목표 위치를 기준으로 가속화된 IK 풀이를 통해 모델 표면을 구성하는 삼각형 메쉬 정점의위치를 계산한다. 이 계산 과정에서 빈번하게 사용되 는 중복항을 사전에 계산해 둠으로써 메쉬 위치 계산에 소요되는 시간을 단축하였으며, 모델의 변형된 모습을 신속하게 결과 화면 으로 확인할 수 있다.
마커는 위치 제약조건으로 작용하므로, 가속화된 IK 풀이 방 법의 실험 결과는 마커의 개수에 따라 달라지는 양상을 보인다. 마커의 개수가 적을수록 모델을 기본 자세로부터 목표 자세로 제어하는 것이 비교적 어렵고, 마커가 많을수록 목표 자세와 가 깝게 제어하는 것이 가능하다. 즉 마커의 수가 많을수록 그 변형 결과 자세가 목표 자세와 비슷해지는 것을 확인할 수 있다. 또한 기존의일반적인 IK 풀이 방법과 비교했을 때 그 연산 속도가 평 균 3.14배 빨라졌으며, 마커의 수가 많을수록 성능 향상이 크게 두드러지는 것을 확인할 수 있었다.
본 연구는 3D 모델 변형에 필요한 IK 풀이를 가속화 된 방법으 로 연산 속도를 개선했다는 데에 의의가있다. 기존의 삼중 중첩 반복 구조의 계산 절차와 달리, 중복항을 사전에 계산함으로써 이중 중첩 반복 구조의 계산 절차를 수행한다. 이러한 개선된 계 산 구조를 통해 모델 변형 결과를 빠르게 구현할 수 있고, 이러한 가속화된 IK 풀이 방법은 3D 모델을 다루는다양한 분야에서 활 용할 수 있다. 예를 들어, LBS 기법으로 구현된 3D 모델을 다루는 데 자연스럽고 빠른 속도의 모델 변형 또는 제어가 가능하다. 또 한 사용자와의 상호작용 인터페이스를 접목하여 3D 모델의 편집 도구로도 응용할 수 있다. 가속화된 IK 풀이 방법은 컴퓨터 비전 분야, 특히 무마커 추적 관련 연구에서 유용하게 활용될 수 있다.
본 연구에서는 모델 표면상에 존재하는 마커들의 목표 위치를 위치 제약조건으로 삼아 IK 풀이를 수행한다. 이는 등식 제약조 건(equality constraints)으로서, 제약조건의 만족을 위해 마커로 선택된 정점의위치 계산에만 변형이 집중되어 부자연스러운 변 형 결과를 도출하기도 한다. 따라서 향후 연구로는 위치 제약조건 이외에도 다양한 제약조건을 적용하여 보다 자연스럽고 안정적 인 변형을 연출하고자 한다. 예를 들어 법선 벡터 제약조건(normal constraints)을 적용할 경우, 법선 벡터를 이용하여 평면의유 무를 확인함으로써 메쉬 관통(penetration) 현상을 개선할 수 있 다. 또한 실루엣 제약조건(silhouette constraints)을 적용할 경우, 목표 자세와 변형 결과 자세 간의 오차를 보완할 수 있고, 이외 에도 광선 제약조건(ray constraints), 평면 제약조건(plane constraints), 여러가지 비동식 제약조건(inequality constraints) 등을 적용하여 결과 품질을 개선할 수 있다. 이렇게 개선된 IK 풀이 방법은 실제 관측 데이터를 활용하는 컴퓨터 비전 기반 어플리케 이션에서 유용하게 도입될 수 있다.










