1. 서론
노이즈는다양한 환경적 요인들로 인해 디지털 영상에서 흔하게 관찰된다. 이러한 노이즈들은 우리가 디지털 영상을 통해 얻고 자 하는 정보들을 분석하고 관찰하는데 방해요소가 될 수 있다. 예를 들어 의료진단 영역에서는 이러한 노이즈들이 정확한 진단 을 방해하고 더 나아가 오진율을 높이는 요소가 된다. 이러한 문 제들을 해결하기 위해 오래전부터 디지털 이미지에서 노이즈를 제거하는 기술은 계속해서 발전해왔다. 디지털 센서와 장비의 발 전으로 노이즈가 감소했지만 특정 영역에서는 아직도 노이즈가 필연적인 요소로 남아있다. 뇌의 구조를 분석하고 원리를 이해하 기 위해 연구가 되는 커넥토믹스 (connectomics) 연구에서 가장 중요한 과정은 뇌의 구조를 디지털화하는 것이다. 뇌의 구조를 디지털화하기 위해서는 많은 연구가 진행되고 있는데, 최근 초고 속 자동 이미징 [2, 3, 4] 장비와 기술이 발전하면서 병목현상을 유발하는 이미징 과정이 대폭 단축됐다. 하지만 Quan et al. [5] 에서 소개된 것처럼 이러한 이미징 방법은 많은 노이즈가 수반 된다. 초고속 자동 이미징 장비에서 발생하는 노이즈들은 여러 다른 종류들이 혼합된 노이즈이기 때문에 전통적인 노이즈 제거 방식으로는 제거가 어려운 문제점이 있다.
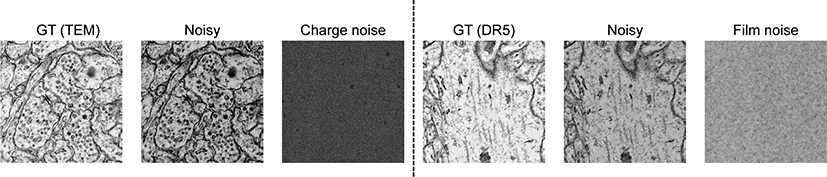
이러한 영상의 노이즈를 제거하기 위하여 우리가 관찰한 노이 즈 영상 이외에 참조할 수 있는 깨끗한 영상이 존재한다면 그 영 상을 활용할 수 있는 방법이 활발하게 연구되어 왔다. 최근 몇 년 동안 심층학습의 발전으로 지도학습의 노이즈 제거 [6, 7] 성능은 비약적으로 발전했다. 이러한 성능을 얻기 위해서는 지도학습은 깨끗한 영상과 노이즈가 섞인 두 쌍의 영상들에 의존한다. 초고속 자동 이미징 장비의 예시에서와같이 관찰된 노이즈가 섞인 영상 과 짝을 이루는 깨끗한 영상은 얻기가 불가능하다. Figure 1에서 보이는 것처럼 우리는 기존에 알고 있는 가우시안 노이즈, 소금-후추 노이즈와 같은 잘 알려진 것과 다른 형태의 노이즈를 볼 수 있다. 이런 경우에는 노이즈의 수학적 통계를 알 수 없기 때문에 주어진 노이즈 이미지와 깨끗한 이미지의 분포만을 참조해야만 한다. 짝을 이루지 않는 (unpaired) 깨끗한 영상의 참조는 성능을 높이기 위한 필수적인 요소이다. 하지만 짝을 이루지 않는 노이 즈 영상과 깨끗한 영상을 사용해 심층학습 모델을 학습하는 것은 어렵다. 두 영상이 짝을 이루지 않는 경우라면 심층학습모델을 학습하기 더욱더 까다로워 진다. Quan et al. [5]에서는 관찰된 노 이즈 영상에 대한 다른 짝이 존재하는 경우 사용 할 수 있는 심층 학습 기반 노이즈 제거 기술을 개발했다. 하지만 깨끗한 영상과 노이즈 영상의 쌍으로 학습시킨 지도학습 기반 심층학습 모델의 성능과 큰 격차가 존재했다.
최근 Lee and Jeong [1]은 자가협동 학습을 통해 짝을 이루지 않는 데이터를 이용한 노이즈 제거 모델의 성능을 크게 개선했 고 지도학습 기반의 방법의 성능에 거의 근접한 성능을 보여줬 다. 자가협동 학습은 자가 적대 공격 (self-adversarial attack) [8] 과같은 문제점을 보여주는 CycleGAN [9]의 한계를 극복하고 더 나아가 커넥토믹스에서 사용되는 초고속 자동 이미징 장비에서 발생하는 노이즈를 획기적으로 복원했다. 이 연구를 통해 우리는 좋은 품질의 노이즈 이미지의 복원영상을 얻기 위해 더는 심층학 습모델을 깨끗한 이미지와 노이즈 이미지의 쌍의 데이터를 통해 학습시킬 필요가 없어졌다. 하지만 Lee and Jeong [1]이 제안한 상호의존적 자가 협동 학습 (ISCL)은 복잡한 다섯 개의 네트워크 로 이루어져 있는데 이 네트워크의 정규화 방법에 대한 최적화가 이루어지지 않았다. 정규화 방법은 위 논문에서 언급된 것과 같 이 성능에 큰 영향을 미치기 때문에, 이번 연구에서는 Lee and Jeong [1]이 제안한 상호의존적 자가 협동 학습 (ISCL) 방법에서 정규화 방법에 대한 논의와 실험을 통해 최적화된 정규화 방법을 찾으려고 한다.
2. 관련 연구
영상의 사전 지식 (prior)을 사용한 패치 (patch) 기반 방법들은 심 층 학습 기법의 발전 이전에 영상 노이즈 제거에서 뛰어난 성능 을 보여줬다. 특히 BM3D [10]의 경우 가우시안 노이즈에 대해서 심층 학습 기법에 비견될 수 있는 수준을 보여준다. 하지만 최근 에는 심층 학습의 계속된 발전으로 전통적인 영상의 사전 지식 기 반 방법들의 성능을 뛰어넘었다. DnCNN [6]에서는 기존의 지도 학습 방법과는다르게 수학적 노이즈 모델을 통해 만들어진 노이 즈 영상을 깨끗한 영상에 더해 합성된 데이터를 만든다. 그렇게 되면 나머지 (residual) 영상과 노이즈 영상 쌍으로 지도 학습을 적용했을 때에 더 안정적인 수렴과 높은 성능을 보여줄 수 있음 을 확인했다. 거기에 더해 배치 정규화 (batch normalization) [11] 이 주어진 모델의 성능을 더욱 신장시킬 수 있음을 확인했다. CaGAN [7] 에서는 생성적 적대 신경망 (generative adversarial network (GAN)) 을 사용해 DnCNN의 과도한 평활화 (smoothing)을 줄여주고 더욱 실제적인 질감을 살릴 수 있는 노이즈 제거 방법을 제시했다. 생성적 적대 신경망에 더해 집중 (attention) 신경망을 더해 성능을 증진했다.
Noise2Noise [12]는 비지도 학습 기반 노이즈 제거 방법으로 처 음 소개가 됐다. 같은 영상에 대한 서로 다른 노이즈를 더해 쌍을 만들어 학습시키는 방법인데 이 방법은 노이즈 통계에 대한 사전 지식이 필요하다. 실제로 우리가 접하는 노이즈 영상들은 노이 즈 통계에 대한 사전 지식이 없는 경우가 많아 실제로 적용이 어 렵다. 이러한 문제를 해결하기 위해 자가감독 학습 기반 노이즈 제거 기술 [13, 14, 15, 16]들이 발전했다. 자가감독 학습 기반 방 법들은 노이즈 영상만을 가지고 있을 때 노이즈 영상만으로 심층 인공 신경망을 학습시키는 방법이다. 노이즈 통계와 깨끗한 영상 에 대한 조건 없이 노이즈 제거를 하는 방식을 블라인드 노이즈 제거 (blind denoising) 이라 부른다. 이 블라인드 노이즈 제거 방 식의 문제점은 노이즈 영상에 의존하는 방식이기 때문에얻고자 하는 깨끗한 영상이 노이즈가 있는 영상의 특성과 너무 다르게 되 면 복원하기 어렵다는 단점이 ISCL [1]에서 보고되었다. 이를 해 결하기 위해서 짝지어지지 않는 깨끗한 영상과 노이즈 영상을 사 용해 심층 신경망을 학습시키는 기법들이 개발되었다. ADN [17] 과 DRGAN [18]은 풀어진 신경망(disentanglement network)과 생 성적적대 신경망(GAN)을 사용해 짝지어 지지 않는 깨끗한 영상 과 노이즈 영상을 사용한 노이즈 제거(unpaired image denoising) 성능을 높였다. 하지만 풀어진 신경망의 경우 많은 오토인코더 (auto-encoder) 손실 함수의 계산으로 인해 계산 비용이 증가하게 되고 이로 인해학습에 드는 시간이 길어진다. ISCL은 새로운 접 근 방식을 제시했는데, 만약 관찰된 노이즈 영상과 얻고자 하는 깨끗한 영상이일대일 대응(one-to-one correspondence)라면 노이 즈를 의미하는 나머지 영상 또한한 개 이상 존재한다라는 가정을 제시했다. 이를 통해 노이즈 제거 모델의 치역을 제약할 수 있는 노이즈 추출 인공 신경망을 모델에 추가했고 이를 자가나머지 학습(self-residual learninig)이라고 부른다. ISCL은 기존의 방법 들보다 뛰어난 노이즈 제거 성능을 보여줬고 더 나아가 모델의 크기는 다른 최신 방법들보다 훨씬 적었다. 이 방법에서는 배치-인스턴스 정규화 [19] 기법을 모든 모델에 적용했다.
심층 인공신경망의 경우 신경망의 깊이가 복잡하고 길어질수 록 그래디언트가 사라지거나(gradient vanishing) 발산하는(gradient exploding) 문제가 있었다. 이를 해결하기 위해서 배치 정규 화 [11] 방법이 제시됐다. 배치 정규화의 경우 배치 단위로 특성의 통계를 정규화 하므로 인스턴스 사이의 변화를 보존할 수 있지만, 인스턴스 정규화 [20] 방법은 인스턴스 사이의 변화를 정규화를 통해 제거하게 된다. 즉, 인스턴스 정규화 기법은 주어진 입력 특 성의 질감이나 빛의 세기를 정규화를 통해 제거하게 된다. 이로 인해 정규화 기법마다 이미지의 모양 또는 질감의 특성을 강조하 거나 무시하게 된다. 이 두 문제를 해결하기 위해서 배치-인스턴 스 정규화 [19] 기법이 제안됐다. 배치-인스턴스 정규화 기법은 훈련 가능한 변수를 적용해 배치 정규화로 얻어진 특성과 인스턴 스 정규화로 얻어진 특성을 결합해 손실함수를 최소화 할 수 있는 적절한 정규화 기법이 선택될 수 있도록 하는 정규화 기법을 제안 했다. 해당 방법은 분류모델에서 기존 배치 정규화 기법보다 더 좋은 성능을 보여줬다. 전환 가능한 정규화 기법 (switchable normalization) [21]은 배치, 인스턴스 정규화 방법 그리고 더 나아가 층 (layer) 정규화 방법 [22]을 서로 전환 가능한 정규화 기법을 제시했다. 이 정규화 방법은 학습 과정을 통해 적절한 정규화 방 법을 선택하기 때문에 적절한 정규화 기법을 찾지 않아도 된다. 하지만 추가적인 계산 비용과 훈련 가능한 파라미터의 증가는 불 필요한 경우가 있을 수 있다. 예를 들어 층 정규화를 적용하면 오히려 학습에 방해가 되는 경우에는 전환 가능한 정규화 기법 대신에 배치-인스턴스 정규화 기법을 적용하는 것이 학습에 더 도움이 될 것이다. 스펙트럼 정규화(spectral normalization) [23] 는 생성적적대 신경망에서 판별자(discriminator)의 불안정한학 습을 보이는 문제점을 해결 할 수 있음을 보여줬다. 다른 정규화 기법과는 다르게 각 층의 출력에 대한 정규화가 아닌 각 층의 가 중치에 대한 수렴 가능 공간을 제한하는 방법이다. 이 논문에서 는 상호의존적 자가협동 학습에서 사용된 생산자, 구분자, 노이 즈 추출을 위한 세 종류의 함수에 적절한 정규화 기법을 적용해 성능을 높이는 것이 목표이다.
3. 방법
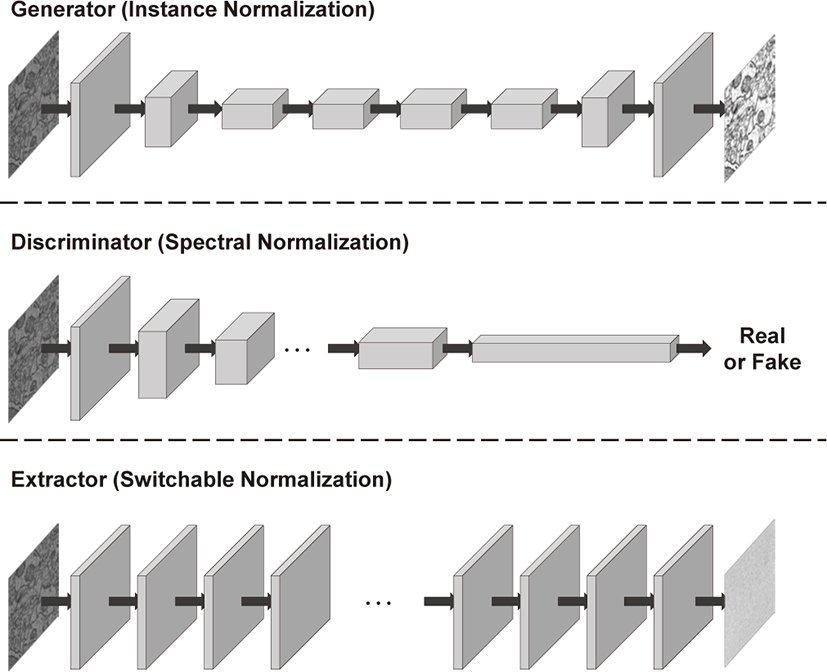
상호의존적 자가협동 학습 [1]은 심층 학습 기반 노이즈 제거 기 술들의 데이터 활용의 한계를 해결하기 위해 개발된 기술이다. 관찰된 노이즈 영상과 짝지어지지 않는 깨끗한 이미지의 통계에 대한 학습을 통해서 비지도 학습 기반인 최신 방법들의 성능을 뛰어넘었다. 이 방법은 크게 생산자, 판별자, 추출자 (extractor)로 이루어져 있다. 생산자가 학습할 때에 판별자와 적대적 학습을 진행하고 추출자에 의해 학습 가능한 잠재 공간이 제약된다. 판 별자가 학습 할때에 생산자에 의해 만들어진 가짜(fake) 데이터뿐 아니라 추출자로 만들어진 가짜 데이터를 추가로 학습에 적용해 판별자의 판별성능을 높인다. 추출자는 생성자에 의해 만들어진 깨끗한 모조 영상을 통해 학습된다. 추출자는 생성자에 의해 만 들어진 모조 영상에 의존하는 학습을 하므로 자가협동 학습이라 불린다. 이렇게 세 가지 모델은 상호의존적으로 반복 학습을 진행 하게 되는데 각 모델은 정규화 층들을 가지고 있다. 모든 모델은 공통으로 배치-인스턴스 정규화를 사용해학습의 안정성과 성능 을 높인다. 본 연구에서는 Figure 2에서와 같이 생성자와 판별자, 그리고 추출자에 적합한 정규화 방법을 적용하고 성능을 높이는 방법을 제시한다.
최근 정규화 기법은 특정 문제에 따라 적합하게 발전해왔다. 가장 먼저 개발된 정규화 기법 중에서 인스턴스 정규화는다음 수식과 같이 배치를 정규화 한다. x ∈ ℝN×H×W×C 는 입력 특성이라고 가정한다. B, W, H, C들은 각각 배치, 넓이, 높이, 채널의 크기를 나타낸다. 인스턴스 정규화의 경우 다음과같다.
, 여기에서 n, i, j, k는 각 차원의 원소에 대한 색인이다. 여기서 γ, β ∈ ℝC는 학습 가능한 어파인 변환(affine transformation) 변 수를 적용해 다음 방정식과같은인스턴스 정규화를 사용한다.
인스턴스 정규화의장점은 배치 크기에 상관없이 동일한 결과를 도출한다. 합성 곱 신경망에서 장점은 훈련 과정과검증 단계에서 사용되는 영상의 크기가 동적이다. 따라서 테스트 노이즈 영상의 크기와 상관없이 훈련과정에서는 영상을 쪼개서 쌓는 방식으로 배치의 크기를 키울 수 있다. 미니배치(mini-batch)의 크기가 커 질수록 성능이 향상되는 것에 대한 연구 [24]는 많이 보고되어 왔다. 이렇게 노이즈 제거 모델의 성능을 높이게 되더라도 테스 트 단계에서 노이즈가 있는 영상의 크기가 크다면 GPU 메모리 의 한계 때문에 배치 크기를 과도하게 줄일 수밖에 없다. 이렇게 된다면 미니배치 안에 데이터가 적어 표본 간의 평균값과 변화 량의 의미 있는 값을 얻을 수 없어 배치 정규화를 사용해 훈련한 모델의 경우 낮은 성능을 야기할 수 있다. 테스트 과정에서 배치 크기를 늘리기 위해 노이즈 영상을 쪼개 쌓게 된다면 나중에 다 시 합치는 과정에서 패치의 경계면에서 노이즈가 발생할 수 있고 이를 해결하기 위해 여러 후처리가 진행되어야 한다. 후처리하게 된다면 실제 심층 학습 모델로 얻어진 결과에서성능이 달라질 수 있다. 이런 부분을 해결하기 위해서 훈련과정 동안 표본 간의 평 균값과 변화량을 저장해두는 방식을 사용하지만, 테스트 영상에 의존하는 값이 아닌 훈련데이터에 의존하는 값이기 때문에 성능 저하를 야기할 수 있다. 또한, 기존의 배치-인스턴스 정규화의 경 우 두 종류의 정규화된 특성에 대해서 융합을 하기 위한 학습을 동시에 해야 하기 때문에 특성을 거의 보존해야 하는 노이즈 제거 방법과 다르게 모델의 복잡도가 올라가기 때문에 적합하지 않다. 더 나아가 모델의 복잡성으로 인해 생성자의 초기 학습속도가 느 려지게 된다면 이후 판별자와 추출자의 성능에 영향을 미치기 때 문에 학습의 복잡도가 낮고 배치 크기에 민감하지 않은인스턴스 정규화를 적용했다.
스펙트럼 정규화의 경우 판별자에 적용했을 때에 하이퍼변수 (hyperparameter)의의존도가 줄어든다고 보고됐다. 그에 더해학 습을 안정화 하는 WGAN [25] 또는 WGAN-GP [26]과 비교해서 도 적대적 생성자 신경망의 성능이 좋았다. 판별자의 각 합성 곱 층에 대해서 우리는 보고된 안정성을 부여하기 위해 다음 방정식 과같은 스펙트럼 정규화를 적용한다.
여기서 σ(W )의 경우 각 층의 가중치 W 에 대한 스펙트럼 노 름 (spectral norm)이다. 방정식 (5)의 경우 각 층의 가중치를 Lipschitz norm으로 나눠줌으로써 Lipschitz 상수의 상계 (upper bound)가 1이 되도록 유도한다. 스펙트럼 정규화의 경우 입력 특 성에 대한 정규화가 아닌 각 합성 곱 신경망의 층을 구성하는 가 중치에 대한 제약조건이다.
우리는 전환 가능한 정규화를 추출자에 대해서 적합한 정규화 로 제안한다. 전환 가능한 정규화란 인스턴스, 배치, 층 정규화에 대한 융합을 최종 정규화로 제안하고 훈련 가능한 상수를 통해 융합의 정도를 학습한다. 가장 먼저 배치 정규화와 층 정규화는 다음 방정식과같다.
전환 가능한 정규화는 이전에언급한 세가지 정규화 방법을 다음 과같이 결합한다
여기서 γ, β ∈ ℝC는 학습 가능한 어파인 변환(affine transformation) 변수이다. 다음 방정식과 같이 훈련 가능한 변수 wb, w′b, wl, w′l, wi, w′i에 의해 배치 정규화된 특성, 층 정규화된 특성, 그리고 인스턴스 정규화된 특성이 결합한다. 전환 가능 한 정규화는 모델의 복잡도가 높아지게 되지만 추출자의 경우 DnCNN [6]에서 보고된 것과 같이 학습의 복잡도가 낮기 때문 에 모델의 복잡도가 높아지더라도 학습에 미치는 영향이 적다. 더 나아가 모델의 복잡도는 학습 이후 간단한 모델보다 더 좋은 성능을 보여주기 때문에 추출자에 적합한 정규화로 전환 가능한 정규화를 제안한다.
4. 결과
이번 실험을 통해 우리가 제안한 방법의 성능을 보여주기 위해 서 우리는 기준인 ISCL의 정규화 방법을 최신 정규화 방법으로 대체하면서 실험을 진행했다. 기준점인 ISCL은 배치-인스턴스 정규화를 사용했고, 더 나아가 우리는 배치-인스턴스 정규화를 대신해 배치 정규화 [11], 층 정규화 [22], 그룹 정규화 [29], 전 환 가능한 정규화 [21]를 사용해 비교했다. 우리는다음 방정식과 같은 그룹 정규화 방법을 사용했다.
g는 그룹의 색인이고 Gg는 g번째 그룹의 집합이다 (e.g., G1 = {1, 2, ..., 32}, G2 = {33, 33, ..., 64}. 본 연구에서 제안된 방법은 각 모델마다 생성자에 대해서는 인스턴스 정규화 [20], 판별자에 대해서는 스펙트럼 정규화 [23], 그리고 추출자에 대해서는 전환 가능한 정규화 [21]를 사용했다. 공정한 비교를 위해서 ISCL에 서 사용한 모든 하이퍼변수들에 대해서 똑같은 환경과 조건으로 실험을 진행했다. 또한 Table 1에서와 같이 합성 데이터 실험인 case 1과 2의 경우 4번의 교차검증 역시 같은 표본들로 검증했 다. 비교 방법은 지도 학습 기반인 DnCNN [6], RED-CNN [27], CaGAN [7]을 선택했다. 비지도 학습으로서는 본 연구의 기초가 되는 Quan et al. [5] ISCL [1]과 최신 짝지어지지 않는 영상 기반 노이즈 제거 방법인 UIDNet [28], ADN [17]을 선택했다.
| Case | Noise-Free Images | Noise Types | Noisy Images (Scenario) |
|---|---|---|---|
| 1 | TEMZB | Charge | TEMZB + Charge (Synthetic) |
| 2 | TEMDR 5 | Film | TEMDR5 + Film (Synthetic) |
| 3 | TEMZB | Charge | SEMZB (Real) |
| 4 | TEMDR 5 | Film | TEMPPC (Real) |
본 연구에서는 공평한 실험을 위해서 Quan et al. [5]과 Lee and Jeong [1]에서 사용한 데이터와 같은 데이터를 사용했다. Table 1 에서와 같이 관찰 대상이 없는 영역에서 촬영한 노이즈 영상을 실제 깨끗한 관찰 영상에 합성해 케이스 1번과 2번 사례를 만들 었다. 케이스 3번과 4번의 경우 실제 사례에서 노이즈만 관찰 가 능한 영상을 사용해 실제 사례에서의 성능을 평가했다. 실제 사 례에서는 관찰된 노이즈 영상에 해당되는 깨끗한 영상이 없기 때문에 시각적인 질적 평가만 가능하다.
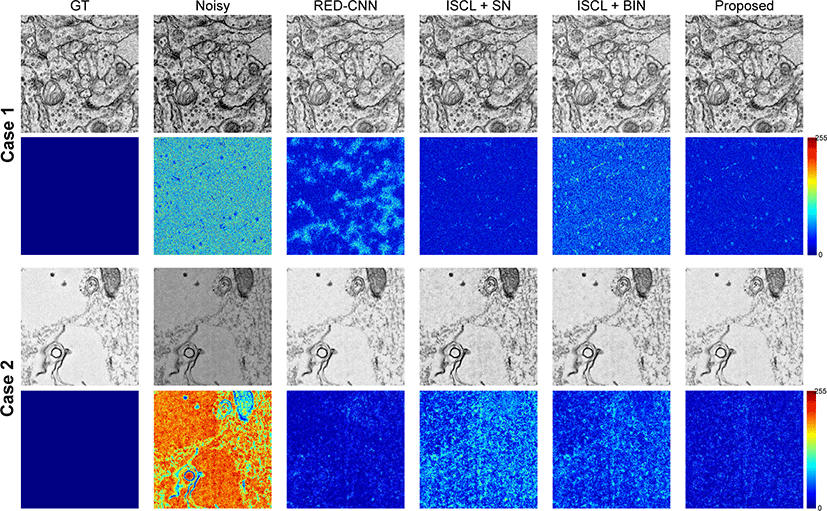
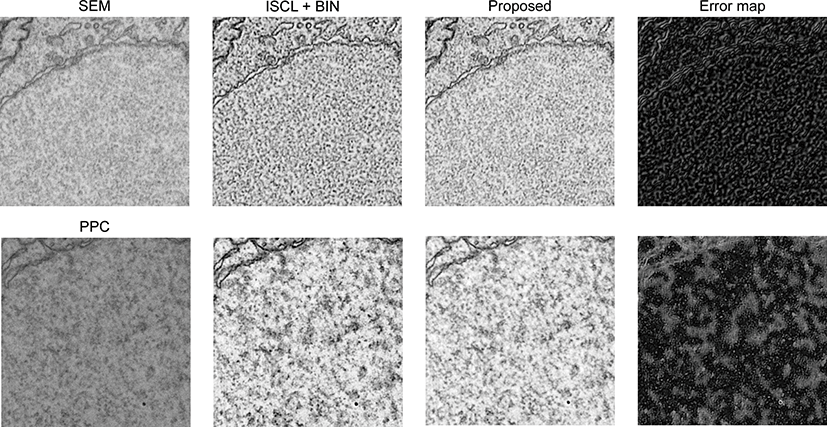
ISCL의 구현은 공개된 공식 코드를 사용했다. 모든 하이퍼변수 는 기존 ISCL의 실험과 동일하게 세팅했다. 그룹 정규화의 경우 그룹의 크기 |Gg|는 32를 사용했고 채널의 수가 32개일 경우 층 정규화와 같아진다. Table 1에서 명시된 것과 같이 case 1과 2에 대한 교차검증의 결과는 Table 2에 요약되어 있다. Table 2에서 보이는 것과 같이 정규화 방법에 따라서 성능 차이가 크다. 3.2 에서 설명한 것 처럼 배치 정규화의 경우 훈련 과정과 테스트 과 정에서의 크기가 다르기 때문에 훈련과정 동안 각 배치 정규화 층마다 평균과 변화량 값을 저장했다가 테스트 과정에서 사용한 다. 하지만 이 값들은 테스트 영상의 값에 따라 변화하는 값이 아닌 훈련 데이터에 의존하는 값이기 때문에 성능에 저하가 발 생한다. Table 2에서 처럼 배치 정규화로 대체했을 때에 성능이 크게 저하되는 것을 볼 수 있다. 더 나아가 배치 정규화는 인스 턴스 정규화의장점인 질감의 변화량을 제거하지 못해 판별자의 성능을 저하할 수 있다. 짝을 이루지 않는 영상 노이즈 제거에서 배치 정규화보다 배치-인스턴스 정규화가 더 좋음을 보여줬다. 또한 층 정규화와 그룹 정규화의 경우 배치 정규화보다 더 좋은 성능을 보여줬다. 배치-인스턴스 정규화는 다른 정규화에 비해 좋은 성능을 보여줬고 필름 노이즈 (film noise)의 경우에는 전환 가능한 정규화와 비슷하거나 더 좋은 성능을 보여줬다. 생성자, 판별자, 추출자에 대해서 모두 같은 정규화를 사용할 때에는 배 치-인스턴스 정규화가가장 좋은 성능을 보여줬지만 제안된 방법 처럼 각 모델의 특성에 적합하게 적용했을 때에는 가장 좋은 영상 품질을 보여줬다. PSNR의 경우 필름 노이즈 실험에서 0.8dB만큼 성능이 향상했다. 특히 주목할 점은 지도학습인 DnCNN과의 비 교에서 필름 노이즈에서 더 좋은 품질의 영상을 얻을 수 있었다. 더 나아가 지도학습 기반의 최신 방법인 CaGAN과 비교해서도 PSNR 0.17dB 정도 차이가 난다. SSIM의 경우 0.0028정도 차이 가 나는 것을 봤을 때 필름 노이즈에서는 지도학습과거의 근접한 성능을 얻을 수 있음을 확인했다. Figure 3에서와 같이 제안된 방 법은 생산자, 판별자, 추출자 모두 같은 정규화 방법을 사용하는 방법인 두 방법 (i.e., ISCL+BIN, ISCL+SN)과 비교해서 더 좋은 품질의 결과를 보여줬다. Figure 3의 두 번째와 네 번째 행에서 제안된 방법이 실측(ground truth)과 비교해 더 적은 오차를 보여 준다. 특히 RED-CNN의 경우 전하 노이즈에 대해서 많은 노이 즈가 존재한다. Figure 3에서 제안된 방법이 시각적 평가에서도 기존의 방법보다 충분한 개선점을 확인했다. Figure 4는 실측이 존재하는 노이즈 영상이 아닌 실제 사례에서의 전하 노이즈 (i.e., case 3)와 필름노이즈 (i.e., case 4)의 결과이다. 기준이 되는 방법 (ISCL+BIN)과 제안된 방법 모두 노이즈 영상에서 경계면과 입자 들이 노이즈 영상보다 명확해졌다. 하지만 기존 ISCL은 노이즈 영상에서 보이는 입자들이 과도하게강조되는 경향이있다. 또한 노이즈 영상에서 관측되는 얼룩진 부분들이 강조되어 나타난다. 오차 지도 (error map)에서 얼룩진 부분에서 차이가 나는 것을 볼 수 있다.
| Type | Method | Charge noise | Film noise | ||
|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | ||
| P.S. | DnCNN [6] | 28.27 | 0.9172 | 27.55 | 0.8964 |
| RED-CNN [27] | 28.61 | 0.9230 | 28.02 | 0.9049 | |
| CaGAN [7] | 28.60 | 0.9186 | 28.03 | 0.9020 | |
| U.S. | Quan et al. [5] | 22.32 | 0.8785 | 23.44 | 0.8288 |
| UIDNet [28] | 23.11 | 0.8592 | 21.34 | 0.7826 | |
| ADN [17] | 25.67 | 0.8686 | 24.37 | 0.8535 | |
| ISCL [1] + Batch Normalization [11] | 24.62 | 0.8969 | 20.63 | 0.7568 | |
| ISCL [1] + Layer Normalization [22] | 24.61 | 0.8945 | 23.99 | 0.8829 | |
| ISCL [1] + Group Normalization [29] | 24.86 | 0.9016 | 24.74 | 0.8879 | |
| ISCL [1] + Switchable Normalization [21] | 25.12 | 0.9044 | 26.80 | 0.8948 | |
| ISCL [1] + Batch-Instance Norm [19] | 27.12 | 0.9054 | 27.06 | 0.8915 | |
| Proposed | 27.11 | 0.9076 | 27.86 | 0.8992 | |
5. 결론
본 연구에서는 최신심층 학습 기반 노이즈 제거 방법들의 문제점 인 짝을이루는 깨끗한 영상과 노이즈 영상의의존성을 해결하는 ISCL 방법을 개선했다. ISCL에서 보여준 성능을 개선하기 위해 서 우리는 생성자, 판별자, 추출자에 따른 각각의 모델의 특성에 적합한 정규화 기법을 통해 최적의 모델을 찾아냈다. 공정한 실 험을 통해서 우리가 제시한 방법이 기존의 배치-인스턴스 정규 화를 사용한 것보다 더 좋은 성능을 보임을 확인했다. 더 나아가 본 연구에서는 정규화 방법이 모델 성능에 미치는 영향을 실험 결과를 통해 간접적으로 확인할 수 있었다. 또한 실제로 깨끗한 데이터가 존재하지 않는 사례에서 노이즈 영상을 복원함으로써 실제 사례에서도 적용 가능함을 보여줬다. 하지만 기존 방법과 비교해서 시각적 평가의 개선점에 대한 논의가 더 필요하다. 이 후 연구에서는 복원된 영상의 차이와 활용 면에서의 차이에 대해 연구를 할 계획이다.









