극 분해 이론을 활용한 MPM기반의 입자 회전 애니메이션

송, 창용; 김, 기훈; 김, 선정; 김, 창헌

doi:10.15701/kcgs.2022.28.4.13

J Korea Comput Graph Soc 2022; 28(4):13-22

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2022.28.4.13

Article

극 분해 이론을 활용한 MPM기반의 입자 회전 애니메이션

송창용¹

, 김기훈¹

, 김선정²

, 김창헌¹^,^*

MPM-Based Angular Animation of Particles using Polar Decomposition Theory

Chang-yong Song¹

, Ki-hoon Kim¹

, Sun-jeong Kim²

, Changhun Kim¹^,^*

Author Information & Copyright ▼

¹고려대학교

²한림대학교

¹Korea University

²Hallym Unversity

^*corresponding author: Changhun Kim/Korea University(chkim@korea.ac.kr)

© Copyright 2022 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jun 10, 2022; Revised: Jul 06, 2022; Accepted: Aug 23, 2022

Published Online: Sep 01, 2022

요약

본 논문에서는 최소 입자 단위의 역동적인 회전 움직임을 나타낼 수 있는 MPM(Material Point Method) 기반 단일 프레임워 크를 소개한다. 우리가 표현하고자 하는 입자는다양한 형상(Shape)을 가질 수 있음과 동시에, 선형(Linear momentum), 회전 (Angular momentum) 운동을 함께 묘사할 수 있다. 그 결과 기존 구형 입자의 선형 움직임만을 나타내던 입자 기반 시뮬레이 션과는 달리, 시각적으로 단일 입자의 역동적인 모습을 표현할 수 있다. 제안하는 프레임워크는 회전 운동을 큰 변형(Large Deformation)으로부터 분해 및 추출 할 수 있다는 점에서 MPM을 활용하였다. 본 기법은 MPM 적분 과정 중 계산되는 변형 구배 텐서(Deformation Gradient Tensor)를 극 분해(Polar Decomposition)하는 과정을 통해 회전 텐서(Rotation Tensor)를 추출 하고, 각 입자의 선형 운동과 함께 이를 적용하여 결과적으로 입자 자체의 회전, 선형 운동을 동시에 표현 하는 것이 가능하다. 본 연구에서는 제안하는 기법의 검증을 위해 바람에 흩날리며 회전하는 입자의 모습 및 움직이는 물체와 정지한 입자간의 상호작용 시뮬레이션을 기존 MPM을이용한 시뮬레이션과의 비교를 통해 진행하였다.

Abstract

In this paper, we propose a single framework based on the MPM(Material Point Method) that can represent the dynamic angular motion of the elementary particle unit. In this study, the particles can have various shapes while also describing linear and angular motion. As a result, unlike other particle-based simulations, which only represent linear movements of spherical (e.g. Circle, Sphere) particles, it is possible to express the visually dynamic motion of them. The proposed framework utilizes MPM, due to the fact that rotational motion can be decomposed and derived from large deformation. During the integration process of the presented technique, a deformation gradient tensor is decomposed by polar decomposition theory for extracting rotation tensor. By applying this together with the linear motion of each particle, as a result, it is possible to simultaneously express the angluar and linear motion of the particle itself. To verify the proposed method, we show the simulation of rotating particles scattering in the wind field, and the interaction(e.g. Collision) between a moving object and them by comparing the traditional MPM

Keywords: 입자 회전 운동; MPM; 변형 구배 텐서; 극 분해 이론

Keywords: Angular movement of Particles; MPM(Material Point Method); Deformation Gradient Tensor; Polar Decomposition Theory

1. 서론

시뮬레이션을 통한 자연 현상의 사실적인 움직임 표현은 컴퓨터 그래픽스 분야에 있어 주요한 연구 주제이다. 그 중에서도 입자 기반 시뮬레이션은 입자의 독립적인 움직임을 이용하여, 상대적 으로 쉽게 동적인 물체의 움직임 표현을 가능케 해 관련 연구가 다양하게 진행되어 왔다[1, 2, 3, 4, 5]. 하지만 이런 입자의 움직 임은 개별 입자의 선형운동만을 표현할 수 있기 때문에, 눈 결정, 알갱이(Granular) 혹은 쌓인 종이들이 바람에 날려 하늘하늘하게 움직이는 그 역동성을 표현하기에는 다소 부족함이 있다. 이런 현상을 표현하기 위해서는 입자 자체의 선형 운동에 추가적으로 회전 운동을 묘사해야 하기 때문이다. 또한, 입자 기반 시뮬레이 션에서 일반적으로 입자는 원 또는 구를 사용하여 나타내는데, 이러한 형상(Shape)은 입자에 회전을 부여하더라도 그 운동이 사 용자에게 잘 드러나지 않는다.

본 논문에서는 이러한 점들을 보완하여 최소 단일 입자 단위 알 갱이들의 역동적인 움직임을 표현하는 프레임 워크를 소개한다. 입자 기반 시뮬레이션에서 단일 입자 단위의 회전운동을 다양한 형상과 함께 적용할 수 있는 기법을 제안하여, 기존에 표현하지 못했던 입자의 움직임을 더동적으로 보이고자 한다. 결과적으로 제안하는 기법은 일반적인 시뮬레이션에서 표현했던 물체의 움 직임과 최소 입자단위에서의 동적인 움직임을 동시에 표현하는 것이 가능하다.

우리는 입자의 회전 움직임을 연속체의 큰 변형으로부터 유 도하기 위해 [6]에서 눈 애니메이션을 표현 하기 위해 제안된 MPM(Material Point Method)을 기반 해석 기법으로 사용한다. MPM은 기존의 유체를 해석하는 FLIP(Fluid Implicit Particle) 기법[3]을 고체 역학 프레임워크로 확장하여 일반화 한 기법 이며, 큰 변형의 계산에 있어 견고하다는 장점이 있다. 기존의 SPH(Smoothed Particle Hydrodynamics)[1], DEM(Discrete Elements Method)[2] 기법도대 변위(Large Displacement)를 표현하 는 것이 가능하지만, MPM은 앞선 기법들과는달리 연속체 역학 의 프레임워크를 사용한다[7].

제안하는 기법은 연속체의 변형을 나타내는 변형 구배 텐서 (Deformation Gradient Tensor)로부터 회전 텐서(Rotation Tensor) 를 추출할 수 있는 극 분해(Polar Decomposition) 과정을 활용한 다. 이 텐서는 입자 각각의 법선 벡터(Normal Vector)에 적용되어 입자 자체에 회전을 부여하며 이를 다양한 오브젝트에 적용해 기 존 기법으로는 표현하지 못했던동적인 형태의 단일 입자 운동을 나타낼 수 있다.

본 논문에서는 최소 단위 입자의 역동적인 움직임을 묘사하기 위해 바람에 흩날리는눈꽃 입자 및 이들의 다른 물체와의 상호작 용을 시뮬레이션 하였으며 기존 MPM과의 비교를 통해 제안하는 기법을 검증하였다.

2. 관련 연구

2.1 MPM (Material Point Method)

MPM은 이전에 유체를 시뮬레이션 하기 위하여 제안된 PIC(Particle-In-Cell)[4], FLIP(The Fluid-Implicit-Particles)[3]을 고체에 적용한 기법이다[7]. MPM의 가장 큰 이점은, 고체의 큰 변형을 동반하는 문제를 해결할 수 있는 견고(Robust)한 방법이 라는 것이다. 그 결과 기존의 FEM(Finite Element Method)[8], FDM(Finite Difference Method)[9]으로 수렴하지 않는 해를 도출 할 수 있다.

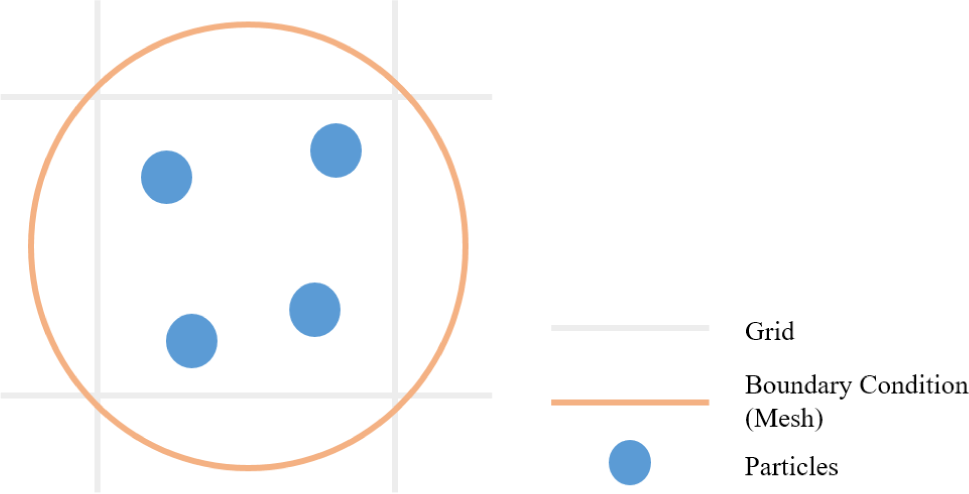
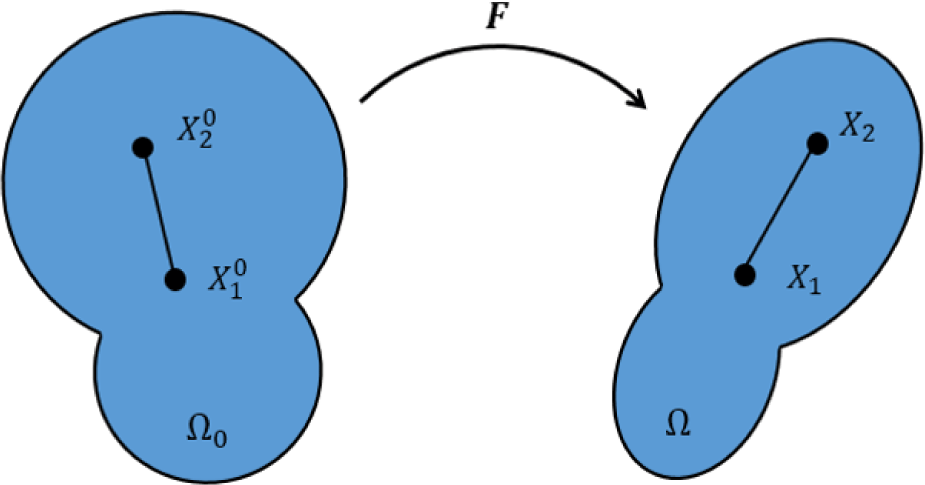
MPM은 기존 입자 기반 시뮬레이션과 동일하게 라그랑지안 질점 입자(Lagrangian Material Point)와 그 이면에 존재하는 격자(Eulerian Cartesian Grid)를 함께 사용하는 격자-입자 하이 브리드 방법이다. 따라서 오브젝트 구성 시 입자간 연결 정보 (Connectivity)를 요구하지 않는다. 대신, 경계 조건(Boundary Condition) 혹은 SDF(Signed Distance Function)을 사용하여 질점 입자 (Material Point)를 오브젝트 내에 분포 시켜 Figure. 1 과 같이 오브젝트를 구성한다. 이후, 입자의 다음 위치를 아래와 같이 계산한다.

Figure 1: Mesh Construction at the MPM

Download Original Figure

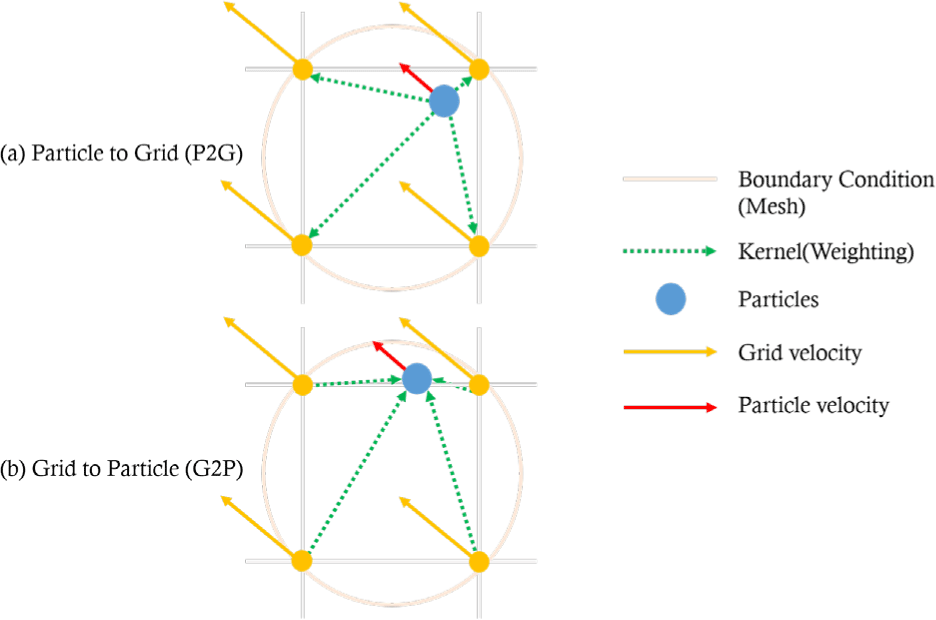
1) Figure.2 (a): 입자의 속도, 질량, 변형 구배 텐서로부터 계산된 힘과같은 물리량들을 입자 주변에 있는 격자(Eulerian)로 거리에 따른 가중치 함수(Kernel)을 사용하여 전달한다.
2) 각 격자는 여러 개의 입자 로부터 전달된 값을 누적하여 구성 방정식에 맞게 적분한다.
3) Figure.2 (b): 입자로 다시 2)에서 계산된 물리량의 가중치에 따른 전달과 함께 다음위치로 입자들을 움직인다.

Figure 2: P2G, G2P Transfer Process

Download Original Figure

MPM의 또 다른 장점은 충돌 처리에 있어 복잡한 수식을 사용 하지 않는 다는 점이다. MPM은 격자를 활용하여 간단하게 처리 가가능하며 입자들을 서로 연결하여 오브젝트를 구성하지 않기 때문에 파괴 혹은 변형 후 그 남은 잔해들을 다시 오브젝트를 형 성하는 재메시화(Re-Meshing) 작업이 필요가 없다[6].

MPM은 컴퓨터 애니메이션 분야에서 많이 활용되고 있으며 초기에는 흐르는 물체를 표현 하기 위한 연구[10]에서 물체의 움직임을 묘사하기 위해 제안되었다[11]. 이후 애니메이션 ‘겨 울 왕국’에서 표현되었던 눈[6]을 시작으로, 모래[12], 거품[13], 옷[14, 15] 과 같이 다양한 물체들을 표현하는데 사용되었으며, [16, 17]에서는 등방성(isotropic) 또는 이방성(Anisotropic) 물체 가 손상 받은 정도를 Griffith의 취성파괴이론[18]과 Phase Field Modeling, Ginzburg-Landau의 상전이이론[19]을 결합하여 균열 의 진전을 묘사하였다. 또 다른 연구로는, [20]은 취성 물체(Brittle Material)와 머리카락과 같은 얇고 기다란 물체들을 표현하는데 MPM을 사용하였다.

하지만 MPM은 데이터를 격자에서 계산하기 때문에 입자보 다 격자의 자유도가 높아 정보량을잃어버리는 소산(Dissipation) 문제가 발생한다는 단점이 있다. 그 결과 수치적인 응집력이 발 생하여 입자들이 서로 뭉치는 경우가 존재한다. 이를 보완하기 위해 [21]은 APIC (The Affine-Particle in Cell Method)를 제안하 였다. 이 기법은 데이터 전달 시 아핀(Affine) 모션을 전달해 주 어 응집력을 줄였다. 한편, 다른 제안으로는 앞서 언급한 [20]의 SFLIP(Separable FLIP), AFLIP(Affine-augmented FLIP)과 이 둘 을 결합한 ASFLIP(Affine-augmented Separable FLIP)이있다. 이 기법들은 기존 FLIP기법으로는 표현 하기 힘들었던 취성 물체 표현 시 직접적으로 속도, 위치 조정자(Velocity, Positional Adjustment)를 추가하여 응집력을 줄임으로써 이를 보완하였다.

이처럼 기존 연구에서는 입자 자체에 초점을 두기 보다는 오 브젝트를 연속체 역학적 관점으로 해석하여 시뮬레이션을 진행 하는 경우가 많았다. 하지만 본 논문에서는 MPM이 큰 변형을 표 현할 수 있다는 점에 기인하여 이로부터 회전을 유도하고, 이를 입자에 적용하여 입자 각각의 역동적인 모습을 간단하게 표현하 는 방법을 제안할 것이다.

2.2 Particle Rotation

최근그래픽스 분야에서 입자 자체의 회전 움직임이 시뮬레이션 과정에 관여하는 연구가 제안되었다. [22]의 경우 유체를 구성하 는 입자를 구로 가정하고, 이들의 각 속도를 표면을 덮는 거품 입자의 선속도로 변환하였다. 결과적으로 거품 움직임에 유체가 관여함으로써 더 그럴 듯한 움직임을 표현할 수 있게 되였다. 하 지만 본 논문에서는 입자의 회전 움직임이 다른 입자의 움직임에 관여만 하는 접근 방식이 아닌, 입자 자체의 회전을 표현한다는 점에서 [22]의 연구와 차이가 있다.

2.3 Polar Decomposition

극 분해 정리[23]는 현재이론에서도, 실질적인 구현에 있어서도 많이 사용되고 있는 정리이다. 특히 변형 구배 텐서에서 극 분 해를 사용하여 신장 텐서(Stretch Tensor)를 얻을 수 있다는 점이 매우 매력적인데, 이는 곧 물체가 초기 상태와 비교하여 얼마나 변형 되었는지를 유도 해 낼 수 있기 때문이다.

Figure 3: Polar Decomposition

Download Original Figure

이러한 장점을 이용하여 다양한 물체를 해석하는 연구가 진 행되었다[24]. 하지만 극 분해 과정은 계산 후 신장 텐서 이외에 회전 텐서(Rotation Tensor)도 유도 해 내는 것이 가능하다. 그 이 유는 외력에 의하여 물체가 변형될 시 제자리에서 변형만 되는 것이 아닌, 회전 운동을 동시에 하기 때문이다. 본 연구에서는 이 러한 물체의 회전을 표현하는 텐서를 그 구성 입자에 적용하여 입자 자체의 더욱 역동적인 운동을 보여주는 방법을 제안한다.

3. 기법 소개

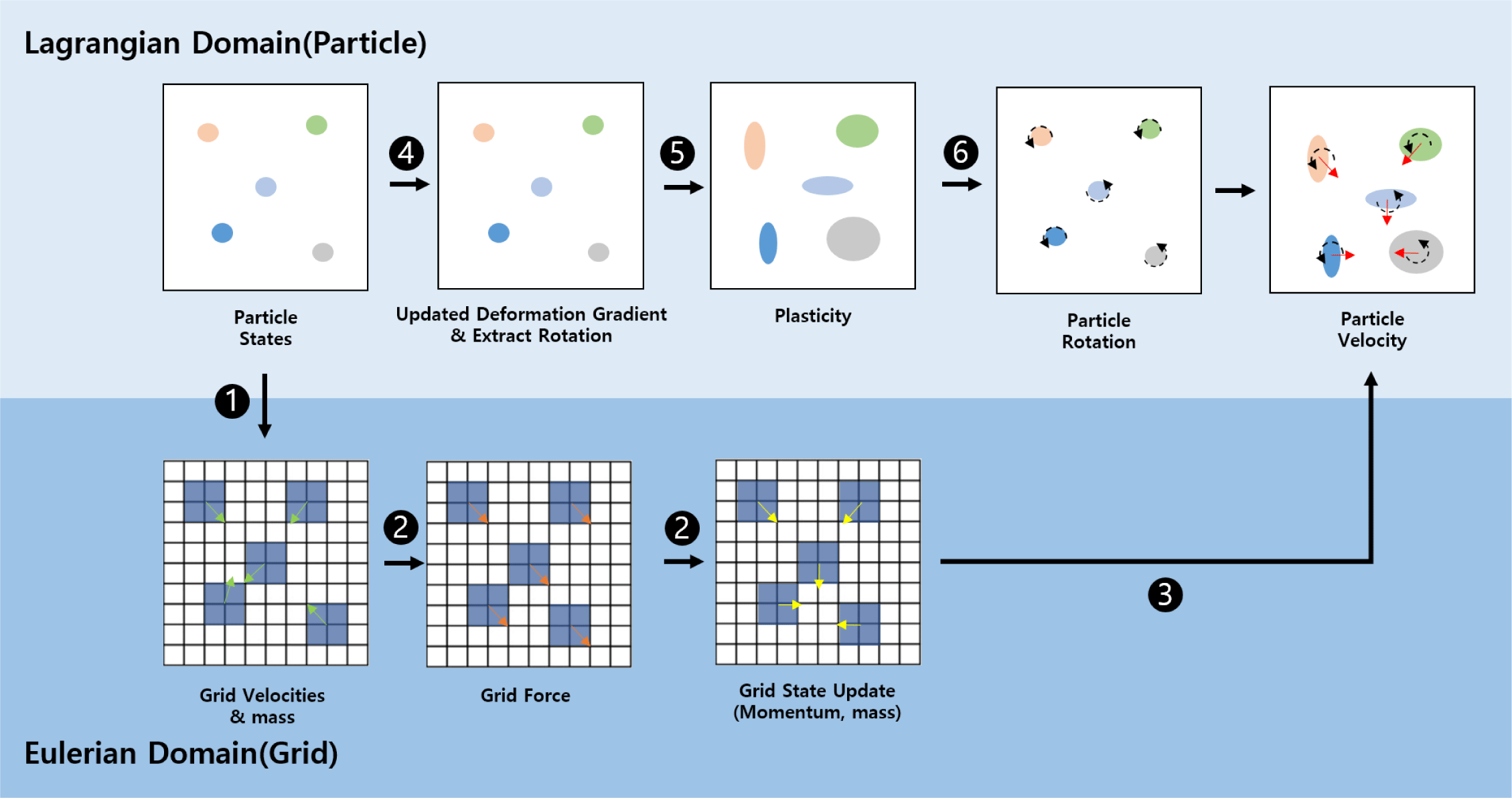
이장에서는 기존 MPM 및 새로 제안하는 기법의 알고리즘을 소 개한다. 본 논문에서 제안되는 알고리즘은 Figure. 4 와 같은 6 가지의 단계로 구성된다.

Figure 4: Method Overview

Download Original Figure

3.1 Full Method

(1) Particles - to – Grid (P2G) 입자의 질량, 운동량 같은 물리 량들이 거리에 따라 보간 되어 격자로 전달된다. 이 과정에서, APIC기법을 사용해 최대한 kernel의 사용으로 인한 정보의 손실 을 줄임과 동시에 더 효율적으로 데이터 전달 과정이이루어진다.
(2) Particle Grid Momentum외부로부터 받은 힘을 Implicit-Backward-Euler방법을 사용하여 적분하여 격자에서의 운동량을 계산한다.
(3) Grid - to – Particles (G2P) APIC를 다시 사용하여아핀 모션을 격자에서 입자로 전달한다.
(4) Deformation Gradient Update Extract Rotation information. 속도 구배(Velocity Gradient)로부터 입자의 변형 구배 텐서를 업데이트 한 뒤 극 분해로 입자의 신장 텐서와 회전 텐서를 분해한다.
(5) Update Particle Plasticity 입자의 변형 구배 텐서를 항복 면에 투영(projection) 하여 소성(plasticity)을 업데이트 한다.
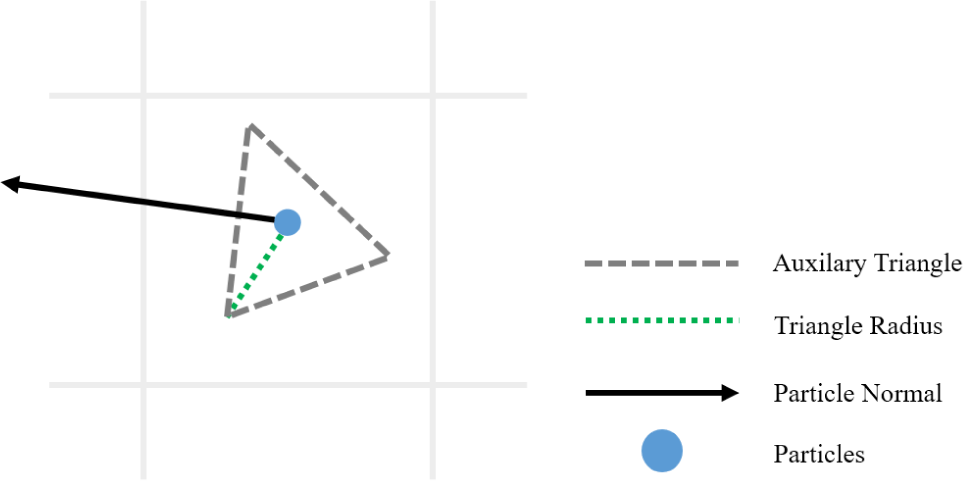
(6) Particle advection 입자의 위치를 이동시킴과 동시에 초기화 시 보조 삼각형으로부터 유도된 방향 벡터에 회전 텐서를 행렬곱 하여 입자의 법선 벡터를 회전시킨다.

일반적인 MPM 기법과 제안하는 기법은 (4), (6)번에서 차이가 있으며, 극 분해 과정과 법선 벡터를 통한 회전 식이 추가된다. 제안하는 기법은 각 입자에 바로 계산을 적용함과 동시에 계산 과정에서 사용되는 값을 회전에 사용하므로 계산 Cost가 낮다는 장점이있다.

3.2 MPM

이번 절에서는 본 논문에서 활용하고 있는 MPM의 적분 과정에 사용되는 APIC [21] 기법을 간단하게 소개한다. 이 기법은 데이 터의 격자-입자간 전달과 동시에 입자의 운동량을 격자에서 계 산하기 위하여 사용된다. 본 논문에서 사용되는 기호(Notation) 들은 Table. 1 에 정리하였다.

Table 1: Notation Summary. p is position of the particles, n is Eulerian Grid, and g is global function.

Symbol	Location	Type	meaning
x_p	p	v	위치
V_p	p	s	부피
m_p	p	s	질량
$v p n$	p	v	속도
F_p	p	m	변형 구배 텐서
n_p	p	v	입자 법선 벡터
x_i	n	v	위치
m_i	n	s	질량
$v i n$	n	v	속도
F_i	n	m	변형 구배 텐서
R	n	m	회전 행렬
S	n	m	인장 행렬
x̂	n	v	변형후 격자위치
Ψ	g	m	에너지 밀도 함수
ϕ	g	m	변형 맵
w_ip	n+p	s	Weighting
t	g	s	타임 스텝
$T p i$	g	v	보조 삼각형 위치

Download Excel Table

3.2.1 APIC (Affine Particle-in-Cell Method)

APIC 연구의 초기에는 강체(Rigid-Body)의 각 운동을 입자-격자 전달 시 보존하기 위하여 RPIC(Rigid Particle-In-Cell Method)[21]를 고려하였다. 하지만 이는 강체가 아닌 물체에 대 해서는 견고함이 부족하였고, 특히 Shearing motion을 표현하는 데 어려움이 있었다. 따라서 RPIC에서 격자에서의 속도를 입자 에 전달해 주는 것이 아닌 3×3 아핀 행렬을 사용하여 문제점을 줄였다. 그 결과 정보의 소산 문제를 줄임과 동시에 다양한 연속 체의 각 운동량을 보존하였다. 세부적으로 말하자면 먼저, 입자 에서 격자로의 운동량 전달은 아래와 같은 식 (1) 을 적용한다.

m i n v i n = ∑ p w i p n m p (v p n + B p n (D p n) − 1 (x i − x p n))

(1)

여기서 $D p n$ 은 관성 텐서(Inertia Tensor)이며 아래와 같은 식 (2) 로 모델링 될 수 있다. 추가적으로 이는 입자-격자 상호 전달 중 아핀 모션을 보존한다.

D p n = ∑ i w i p n (x i − x p n) (x i − x p n) T

(2)

마지막으로 격자에서 다시 입자로의 전달은 다음과같은 식 (3) 으로 모델링 할 수 있다.

B p n + 1 = ∑ i w i p n v ˜ i n + 1 (x i − x p n) T

(3)

이 기법은 물체 전체의 각 운동에 대한 움직임을 보존한다는 장점이 있지만, 본 논문에서 제안하는 입자 자체의 회전 운동을 표현할 수 없다는 점에서 차이가 있다.

3.2.2 Stress-based forces & Linearization

MPM에 있어 외부로부터 물체가 충격을 받아 변형되었을 때의 전체적인 탄성 퍼텐셜 에너지는 격자 기반 에너지 밀도 함수를 사용하여 다음과같은 식 (4) 로 나타낸다[6].

∫ Ω 0 Ψ (F E (X), F P (X)) d X

(4)

Ω₀ 는 물체의 변형되지 않은 모습이다. Stress-based force는 이 를 미분한 것과 같은데, 여기서 특이한 점은 실질적으로 격자 자 체는 변형시키지 않는다는 것이다. 일반적으로 외부에서 힘을 받 게 된다면 물체와 더불어 격자도 그에 상응하여 변화할 것이라고 여겨지지만, MPM에서는 실질적으로 이를 변형시키지 않는다. 그 대신 Euler 방법을 적용하여 아래와 같이 변형된 위치를 격자 현재 속도를 사용하여 식 (5) 와 같이 허상으로 결정한다[6].

x^i = x^i + Δ t v i

(5)

앞서 소개한 에너지 밀도 함수를 위의 식으로부터 결정된 허 상의 격자의 위치 x̂_i를 대입하여 적분을 근사하게 되면 아래와 같은 식 (6) 을유도 해 낼 수 있다. 아래 식에서 격자위치 x̂_i는 x̂ 로 대체하여 표현하였다.

Φ (x^) = ∑ p V p 0 Ψ (F E p (x^), F P p (x^))

(6)

여기서 V 는 입자 각각의 부피를 나타내며 위의 근사식의 도함 수(Derivative)를 유도하게 되면 다음 식 (7) 과 같이 Stress-based force를 근사 할 수 있다.

− f i (x^) = ∂ Φ ∂ x i^(x^) = ∑ p V p 0 ∂ Ψ ∂ F E (F^E p (x^), F P p) (F E p n) T ∇ w i p n

(7)

일반적인 MPM의 경우 위와 같이 격자에 가해지는 힘을 계산 한 후 Semi-Implicit Update 과정을 통해 격자의 다음 단위시간에 서의 속도를 갱신한다. 이후 도출된 격자 속도의 구배를 사용하 여 입자의 변형 구배 텐서를 업데이트 하게 된다. 본 논문에서는 격자의 속도 갱신의 과정은 생략하고, 다음 장에서 변형 구배 텐 서의 업데이트 과정과 새로운 알고리즘을 소개한다.

3.3 변형 구배 텐서의 갱신, 분해와 회전적용

이 장에서는 물체의 변형 구배 텐서의 갱신 방법과 이를 극 분해 를 사용하여 인장과 회전의 2가지 텐서로 분해한 뒤 입자 자체를 회전시키는 새로운 기법에 대하여 소개한다.

3.3.1 변형 구배 텐서의 갱신

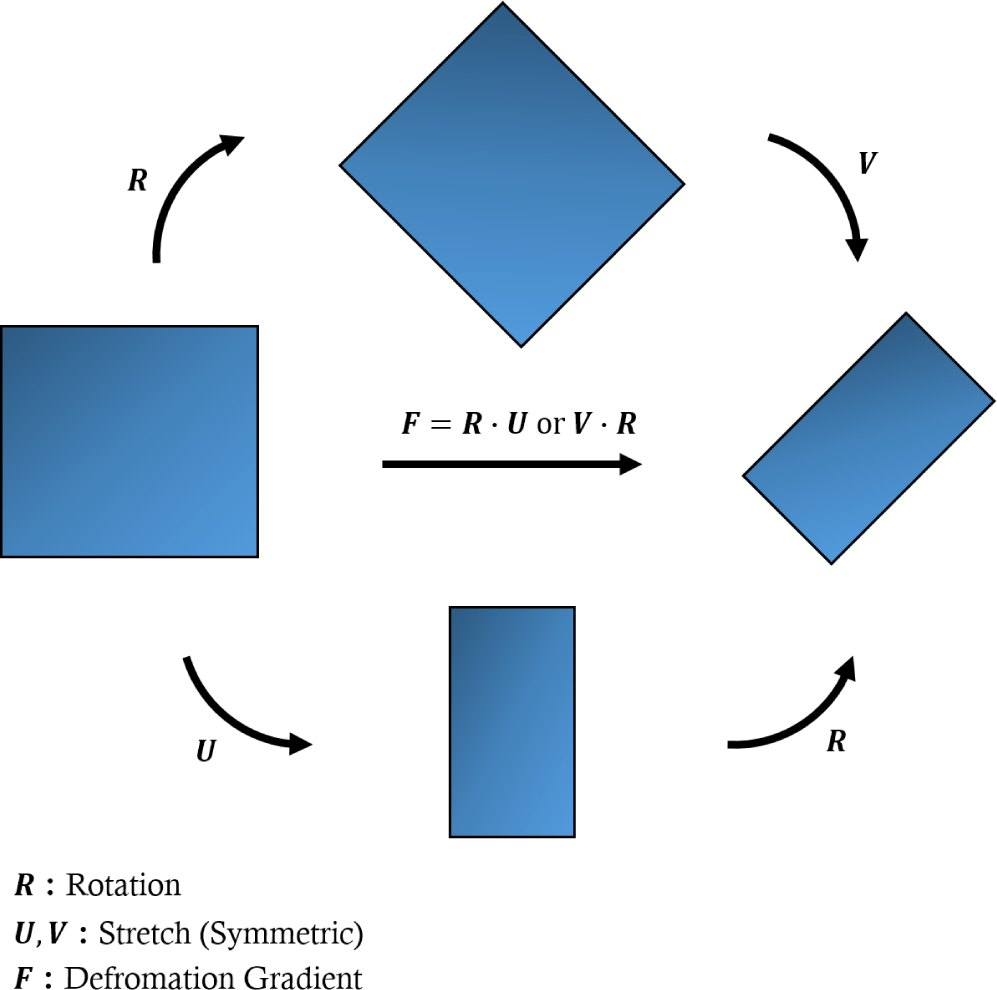
변형 구배 텐서 $F = ∂ ϕ ∂ X$ 는 일반적으로 Figure. 5 의 예시와 같이 물체의 변형과정을 계산하기 위해 주로 사용된다. 본 과정에서, X는 라그랑지안 관점으로 본 물질 내 입자의 좌표이며 ϕ(X, t) 는 변형 매핑 (Deformation mapping)함수이다. 이 함수의 역할은 특정 시간에서의 변형후현재 상태(Deformed Current Configuration)를 변형 전 초기 상태(Undeformed Reference Configuration) 로부터 매핑(Mapping)하는 역할을 한다.

Figure 5: Deformation Gradient

Download Original Figure

결과적으로, 변형 구배 텐서는 이 변형 맵의 도함수(derivative) 라고 할 수 있다. 일반적인 MPM에서는 각 단위 시간이 진행되며 F가 업데이트 되는데, 이를 다음과 같은 식 (8) 으로 표현할 수 있다[6].

∂ ∂ t F (X, t) = ∂ v ∂ X (ϕ (X, t), t) F (X, t)

(8)

여기서 $∂ v ∂ X$ 값은 앞선 장에서 언급한 격자의 속도의 구배 이다. 하지만 본 논문에서 사용된 MPM은 추후 언급될 MLS-MPM(Moving Least Squares Material Point Method)을 사용한다. (4.1 참조) 따라서 식 (8) 의 속도 구배를 APIC의 아핀 모션 $C p n + 1$ 로 수정하여 식 (9)와 같이 계산한다.

F p n + 1 = (I + Δ t C p n + 1) F p n C p n + 1 = ∂ v^n + 1 ∂ x

(9)

3.3.2 변형 구배 텐서의 갱신

물체는 외부에서 힘을 가할 시 찌그러지거나 부서지는 등 그 형 상에 변화가 일어남과 동시에 이동하거나 회전하게 된다. 이 과 정에서, 극분해를 활용하여 변형 구배 텐서를 변형에만 관여하는 인장 항 S와 순수하게 물체를 회전시키는 회전 항 R 로 아래와 같이 분해할 수 있다.

F p = U p Σ p V p T = S p R p

(10)

R p = U p V p T S p = U p Σ p U p T

(11)

본 기법에서는 이처럼 변형 구배 텐서 업데이트 이후 각 입자의 회전 항을 식 (11)로부터 유도한다. 그 후 입자를 보조하는 허상의 삼각형을 Figure. 6 와 같이 사용하여 입자의 법선 벡터를 초기화 단계에서 계산하고, 이후 시뮬레이션 진행 도중 회전 항을 단위 시간 마다 곱하여 입자자체를 회전시킨다. 초기화 단계 시 보조 삼각형을 사용함으로써 주변 입자를 찾아 법선 벡터를 계산하는 복잡한 과정을 줄여 결과적으로 빠른 연산이 가능하다.

Figure 6: Auxiliary Triangle with particle.

Download Original Figure

n p = (T p x − T p y) (T p z − T p y)

(12)

n p t + 1 = η R p n p t

(13)

입자의 회전정도를 다양하게 표현하기 위하여 회전 행렬을 오 일러 각(Euler Angle)으로 변환한 뒤 회전수정자 η로 스케일링 (Scaling)하여 사용하였으며, 계산된 입자의 법선 벡터는 ply 파 일로 export되고 렌더링 시 이용된다. 위의 식 (13) 을 사용하여 단순한 원, 구와 같은 형상이 아닌 다양한 오브젝트의 선형 운 동에 회전 운동을 추가할 수 있게 되고, 이로 인하여 결과적으로 입자 자체의 역동적인 움직임의 표현이 가능하다.

4. 구현

이 절에서는 본 논문을 구현하는데 사용된 그래픽스 라이브러 리와 바람, 렌더링과 같은 세부 구현 사항을 소개한다. 구현은 NVIDIA GeForce RTX 3080ti 그래픽카드, Intel i7-11700K CPU 및 메모리 32GB 환경에서 이루어졌으며, 제안하는 새로운 기법 을 사용하여 흩날리는눈꽃과 자동차와 충돌하는눈꽃을 모델링 하였다.

4.1 Taichi-Lang

4.1.1 Taichi & Performance

제안하는 기법을 구현하기 위해 “Taichi-Lang” 라이브러리를 사 용하였으며 이는 [25]에서 제안된 MPM 기반 그래픽 라이브러 리이다. 이 라이브러리의 기반이 된 기법은 일반 적인 MPM 과는 유사하나, 더 빠르게 물리 데이터의 근사가 가능하도록 갤러킨 방법(Element-Free Galerkin method, EFG)[26, 27]과 기 존의 MPM을 결합한 MLS–MPM(Galerkin Style Moving Least Squares MPM)[28]을 기반으로 구성되었다. 그 결과 각 방정식의 해를 갤러킨 방법으로 근사 하여 일반 MPM보다 최대 2배 속도가 향상되었음과 동시에, 입자-격자 전달은 APIC를 사용하여 물리 량의 소산 문제를 최대한 줄여 정확성을 높였다.

4.1.2 Taichi & Rendering

Taichi는 비록 연산 속도가 매우 빠르다는 장점이 있지만, 아직 라이브러리 자체 단계의 다양한 렌더링은 지원하지 않는다. 이는 Figure. 7에서도 볼 수 있는데, 각 입자들의 화면으로의 출력을 삼각형, 원의 형상으로 GUI(Graphic User Interface)환경에 서 간 단하게만 지원한다. 따라서 각 입자들의 위치 연산 후 추가적인 렌더링 절차가 필요하다. 이러한 점을 보완하기 위하여 “Taichi-Tina”와 같은 외부 추가 라이브러리를 지원하기도 하지만, 렌더 링 중 액체나 모래와 같은 물체가 아닌 입자 자체가 회전하는 모 습을 묘사하기에는 다소 낮은 기대치를 보였다. 하지만, Taichi 는 ply, obj, jpg, png 등 다양한 파일들의 IO를 지원한다. 따라서 본 논문에서는 각 Frame에서의 ply 파일을 Taichi에서 Export 하 여 Blender로 불러와 렌더링 과정을 진행하였다. 이후 Blender에 서 각 Frame을 연속적으로 재생하는 “Stop-Motion OBJ” 애드온 (Add-On)으로 시뮬레이션을 구성 및 재생하였으며, 이후 눈 입 자에 오브젝트 적용과같은 추가적인 렌더링 과정을 진행하였다.

Figure 7: Taichi-Lang Snow Simulation

Download Original Figure

4.2 Wind Field

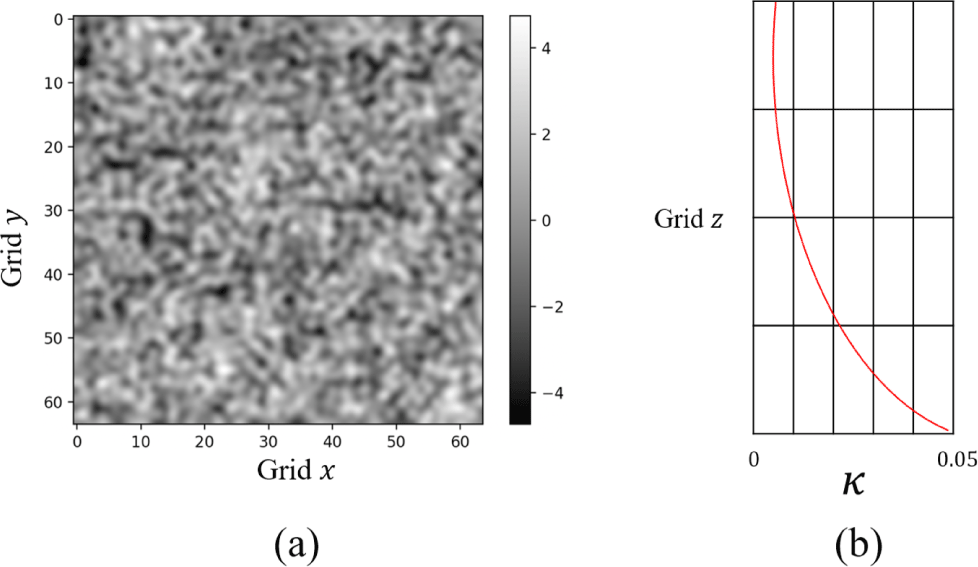
시뮬레이션 중 입자의 회전 및 이동을 역동적으로 표현하기 위 하여 바람을 인위적으로 중력 G과 함께 격자의 초기 속도 v_i에 추가적으로 부여하였다. 특히, 비 정기적인 바람의 모습을 표현 하기 위하여 2차원 펄린 노이즈(Perlin Noise)를 사용하였으며 좌 표에 따른 노이즈 값을 x, y 축 방향으로 적용하였다.

이로 인하여아래로 입자가 떨어질 때 직선으로 자유 낙하하지 않고 노이즈지속성(Persistence)에 따라 다른 진폭을 가진 곡선을 그리며 낙하하는 장면을 구성할 수 있었으며, 이는 더욱 역동적인 장면을 표현 가능케 하였다.3차원 공간 임에도 불구하고 2차원 펄린 노이즈를 사용한 이유는 계산 비용(Cost)가 훨씬 낮았기 때 문이다. 하지만, 그 결과 고도에 따른 바람을 표현할 수 없었기에, [29]에서 제안 한 Scale function κ(G, t)를 노이즈 함수에 적용 하였다(Figure. 8). 격자의 z축을 기준으로 바람을 수정함으로써 결과적으로 입자가고도에 따라 바람에 더 불규칙적으로 영향을 받도록 하는 것이 가능하였다.

Figure 8: (a): 2D Perlin Noise, Grid = 64, Persistence = 1.5, Octave = 4, Resolution (4 x 4) , (b): Scaling function κ(G, t).

Download Original Figure

5. 결과

Figure. 9 는 기존 MPM 기법과 제안하는 기법을 각각 시뮬레이 션 한 것을 동일한 프레임을 기준으로 촬영한 결과이다. 바람과 중력의 경우 모두 동일한 조건을 부여하였으며, 이외에도 상세한 다른 물리적 조건들은 Table. 2 와 같이 설정하여 시뮬레이션을 진행하였다. 두 기법의 Frame을 비교하였을 때 눈꽃의 회전 운동 에서의 결과 움직임의 차이를 보인다. 기존 모델은 회전에 따른 입자 자체의 운동이 보이지 않는다. 눈꽃 입자들이 바람에 영향을 받음에도 불구하고 모두 일정한 방향을 가지고 아래로 떨어지는 모습이 관찰되어어색하게 보여지는 반면, 제안하는 기법은 각각 의 눈꽃의 회전 운동이 바람의 방향에 따라 명확하게 관찰된다. 이는 변형 구배 텐서가 바람과 중력 등 외력에 영향을 받아 변 하였기 때문이며, 이는 입자의 회전 운동으로 치환되었고, 이는 입자의 역동적인 움직임을 보여주었다. Figure. 10 은 제안하는 기법을 연속적으로 촬영한 결과이며 Figure. 11 에서는 움직이는 물체와 눈꽃 간 충돌 및 회전 시뮬레이션의 결과이다.

Figure 9: Compare with MLS-MPM [] at the scattering snowflakes scene. (a): MLS-MPM, (b): Ours. L to R: 40, 70, 100 Frame

Download Original Figure

Table 2: Simulation Parameters.

Parameter	Value
Critical Compression	2.5 × 10⁻2
Critical Stretch	4.5 × 10⁻3
Hardening coefficient	10
Initial density	6 × 10²
Initial Young’s modulus	5 × 10⁻3
Poission’s Ratio	0.3

Download Excel Table

Figure 10: Scattering snowflakes Scene, (a): 34 Frame, (b): 47 Frame, (c): 54Frame, (d): 62Frame, (e): 74Frame, (f): 91 Frame

Download Original Figure

Figure 11: Snowflakes – car collision scene, (a): 70 Frame, (b): 90 Frame, (c): 110 Frame

Download Original Figure

6. 결론 및 향후 연구

본 논문에서는 MPM 기법 시뮬레이션에서 입자의 회전 움직임을 적용하는 방법을 제안하였다. 그 결과, 기존의 방법과 비교하여 최소 입자 단위의 움직임을 더 생동감 있도록 해 주었으며 간단 한 구현을 통하여 표현할 수 있었다. 다만 본 연구는 아직까지 움직이는 물체와의 상호작용 및 입자에 입혀지는 오브젝트 자체 변형의 처리는 불안정하다. 정지한 물체는 주위의 격자의 속도 가 없기 때문에 자연스럽게 이에 영향을 받는 변형 구배 텐서도 사라져 결과적으로 입자의 회전도 멈추게 된다. 하지만 움직이는 물체의 경우 여전히 주변 격자의 속도가 존재하기 때문에 충돌 이후에도 계속 입자가 회전할 가능성이 존재한다. 또한 다양한 오브젝트를 한 번에 입자들에 손쉽게 적용할 수 있다는 장점이 있으나, 변형시키기 위해서는 추가적으로 계산이 필요하다. 추후 움직이는 물체와의 상호작용과 입자 사이의 회전 운동과 함께 병 합, 분해의 연구와 함께 [30]에서 제안한 기법과 유사한 점짐합 렌더링을이용하여 최적화도 진행할 예정이다.

감사의 글

이 논문은 2022년도 정부 (과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원 (No.2022-0-00288, 실감콘텐츠핵심기 술개발 (R&D) 사업, 50%)과 2019년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임 (NRF-2019R1A2C1008244, 중견연구자지원사업, 50%)

References

[1].

J. J. Monaghan, “Smoothed particle hydrodynamics,” Annual review of astronomy and astrophysics, vol. 30, pp. 543–574, 1992.

[2].

F. A. Tavarez and M. E. Plesha, “Discrete element method for modelling solid and particulate materials,” International journal for numerical methods in engineering, vol. 70, no. 4, pp. 379–404, 2007.

[3].

J. U. Brackbill and H. M. Ruppel, “Flip: A method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions,” Journal of Computational physics, vol. 65, no. 2, pp. 314–343, 1986.

[4].

F. H. Harlow, “The particle-in-cell method for numerical solution of problems in fluid dynamics,” Los Alamos National Lab.(LANL), Los Alamos, NM (United States), Tech. Rep., 1962.

[5].

김종현 et al.,“안정적이고 이방성한 빙결 모델링을위한 암 시적 비압축성 유체와 얼음 입자간의 상호작용 기법,” Journal of the Korea Computer Graphics Society, vol. 26, no. 5, pp. 1–13, 2020.

[6].

A. Stomakhin, C. Schroeder, L. Chai, J. Teran, and A. Selle, “A material point method for snow simulation,” ACM Transactions on Graphics (TOG), vol. 32, no. 4, pp. 1–10, 2013.

[7].

W. T. Sołowski, M. Berzins, W. M. Coombs, J. E. Guilkey, M. Möller, Q. A. Tran, T. Adibaskoro, S. Seyedan, R. Tielen, and K. Soga, “Material point method: Overview and challenges ahead,” Advances in Applied Mechanics, vol. 54, pp. 113–204, 2021.

[8].

O. C. Zienkiewicz, R. L. Taylor, R. L. Taylor, and R. L. Taylor, The finite element method: solid mechanics. Butterworth-heinemann, 2000, vol. 2.

[9].

G. D. Smith, G. D. Smith, and G. D. S. Smith, Numerical solution of partial differential equations: finite difference methods. Oxford university press, 1985.

[10].

Y. Zhu and R. Bridson, “Animating sand as a fluid,” ACM Transactions on Graphics (TOG), vol. 24, no. 3, pp. 965–972, 2005.

[11].

D. Sulsky, Z. Chen, and H. L. Schreyer, “A particle method for history-dependent materials,” Computer methods in applied mechanics and engineering, vol. 118, no. 1-2, pp. 179–196, 1994.

[12].

G. Klár, T. Gast, A. Pradhana, C. Fu, C. Schroeder, C. Jiang, and J. Teran, “Drucker-prager elastoplasticity for sand animation,” ACM Transactions on Graphics (TOG), vol. 35, no. 4, pp. 1–12, 2016.

[13].

Y. Yue, B. Smith, C. Batty, C. Zheng, and E. Grinspun, “Continuum foam: A material point method for shear-dependent flows,” ACM Transactions on Graphics (TOG), vol. 34, no. 5, pp. 1–20, 2015.

[14].

C. Jiang, T. Gast, and J. Teran, “Anisotropic elastoplasticity for cloth, knit and hair frictional contact,” ACM Transactions on Graphics (TOG), vol. 36, no. 4, pp. 1–14, 2017.

[15].

Q. Guo, X. Han, C. Fu, T. Gast, R. Tamstorf, and J. Teran, “A material point method for thin shells with frictional contact,” ACM Transactions on Graphics (TOG), vol. 37, no. 4, pp. 1–15, 2018.

[16].

J. Wolper, Y. Fang, M. Li, J. Lu, M. Gao, and C. Jiang, “Cd-mpm: continuum damage material point methods for dynamic fracture animation,” ACM Transactions on Graphics (TOG), vol. 38, no. 4, pp. 1–15, 2019.

[17].

W. Joshuah, C. Yunuo, L. Minchen, F. Yu, Q. Ziyin, L. Jiecong, C. Meggie, and J. Chenfanfu, “Anisompm: Animating anisotropic damage mechanics,” ACM Transactions on Graphics (TOG), vol. 39, no. 4, pp. 37–1, 2020.

[18].

A. Griffith and J. J. Gilman, “The phenomena of rupture and flow in solids,” Transactions of the ASM, vol. 61, pp. 855–906, 1968.

[19].

L. D. Landau, The classical theory of fields. Elsevier, 2013, vol. 2.

[20].

Y. Fei, Q. Guo, R. Wu, L. Huang, and M. Gao, “Revisiting integration in the material point method: a scheme for easier separation and less dissipation,” ACM Transactions on Graphics (TOG), vol. 40, no. 4, pp. 1–16, 2021.

[21].

C. Jiang, C. Schroeder, A. Selle, J. Teran, and A. Stomakhin, “The affine particle-in-cell method,” ACM Transactions on Graphics (TOG), vol. 34, no. 4, pp. 1–10, 2015.

[22].

K.-H. Kim, J. Lee, C.-H. Kim, and J.-H. Kim, “Visual simulation of turbulent foams by incorporating the angular momentum of foam particles into the projective framework,” Applied Sciences, vol. 12, no. 1, p. 133, 2021.

[23].

A. Hoger and D. E. Carlson, “Determination of the stretch and rotation in the polar decomposition of the deformation gradient,” Quarterly of applied mathematics, vol. 42, no. 1, pp. 113–117, 1984.

[24].

P. F. Pai, A. N. Palazotto, and J. M. Greer Jr, “Polar decomposition and appropriate strains and stresses for nonlinear structural analyses,” Computers & structures, vol. 66, no. 6, pp. 823–840, 1998.

[25].

Y. Hu, “Taichi: An open-source computer graphics library,” arXiv preprint arXiv:1804.09293, 2018.

[26].

T. Belytschko and M. Tabbara, “Dynamic fracture using element-free galerkin methods,” International Journal for Numerical Methods in Engineering, vol. 39, no. 6, pp. 923–938, 1996.

[27].

T. Belytschko, Y. Y. Lu, and L. Gu, “Element-free galerkin methods,” International journal for numerical methods in engineering, vol. 37, no. 2, pp. 229–256, 1994.

[28].

Y. Hu, Y. Fang, Z. Ge, Z. Qu, Y. Zhu, A. Pradhana, and C. Jiang, “A moving least squares material point method with displacement discontinuity and two-way rigid body coupling,” ACM Transactions on Graphics (TOG), vol. 37, no. 4, pp. 1–14, 2018.

[29].

T. Hädrich, M. Makowski, W. Pałubicki, D. T. Banuti, S. Pirk, and D. L. Michels, “Stormscapes: simulating cloud dynamics in the now,” ACM Transactions on Graphics (TOG), vol. 39, no. 6, pp. 1–16, 2020.

[30].

민혜정, 김영준, et al., “Gpu 가속을이용한 점집합 렌더링을 위한 전역 조명기법,” Journal of the Korea Computer Graphics Society, vol. 26, no. 1, pp. 7–15, 2020.

[31].

D. Sulsky, S.-J. Zhou, and H. L. Schreyer, “Application of a particle-in-cell method to solid mechanics,” Computer physics communications, vol. 87, no. 1-2, pp. 236–252, 1995.