1. 서론
게임 등 실시간 응용 분야에서 사용자의 의도와 주변 조건을 반영한 사실적인 캐릭터의 동작을 신속하게 생성하는 것은 중요하며 이는 사용자가 캐릭터와의 상호작용을 자연스럽고 직관적으로 느낄 수 있도록 하는 데 이바지한다. 예를 들어, 액션 게임에서 플레이어가 캐릭터에게 특정 동작을 지시할 때, 게임은 해당 동작을 실시간으로 인식하고 반응하여 원활한 게임 플레이를 제공해야 한다.
일반적인 동작 생성 분야에서는 계산의 효율성 및 결과의 사실성으로 인해 모션 캡처에 기반한 동작 합성 기술이 널리 사용되고 있다. 이 기술은 실제 배우 또는 애니메이터가 수행한 동작을 포착하여 캐릭터에게 적용하는 방식으로 동작을 생성하며, 이때 단순 동작의 재생이 아닌 생성 시 사용자의 의도와 주변 조건들이 반영되도록 하는 조작성(또는 반응성)을 갖도록 적용해야 하는 이슈가 항상 중요하게 다뤄졌다.
이를 해결하기 위해 그동안 동작 포착에 기반한 많은 동작 합성 연구 결과가 발표되어왔으나, 그중 비교적 최근에 발표된 모션 매칭 기술은 그 구현의 간단함과 실제 게임과 같은 응용 분야에서의 활발한 활용을 통해 입증된 활용성으로 현재 가장 실용적인 기술 중 하나로 간주되고 있다[12]. 모션 매칭은 간단한 특징 벡터를 정의하고 사용자의 요구조건을 반영하여 최적의 자세들을 입력 동작으로부터 검색하여 합성하는 방식의 기술로, 간단한 특징 벡터의 사용은 검색의 효율성을 높이고 구현의 편의성을 제공한다. 그러나 반대로 특징 벡터의 선택은 생성된 동작의 품질에 큰 영향을 미치게 되며 경험이 없는 사용자는 효과적인 특징 벡터를 선택하고 정의하는 것이 직관적이지 않아 어려움을 격을 수 있다.
본 논문은 다양한 시나리오에서 특징 벡터 선택의 효과성을 검증함으로써, 모션 매칭을 구현하고자 하는 사용자들에게 도움을 제공하는 것을 목적으로 한다. 모션 매칭 기술을 처음 접하고 적용하는 사람들이 특징 벡터를 어떻게 정의해야 하는지에 대한 고찰을 제공하고, 이를 통해 더욱 정확하고 효율적인 모션 매칭을 구현하여 원하는 동작을 캐릭터에 반영할 수 있게 하려 한다. 특히 본 연구에서 집중하고 있는 것은 보행 동작 생성에 있어 효과적인 특징 벡터의 정의이다. 주된 적용 시나리오는 사용자가 원하는 궤적을 따라가는 자연스런 동작을 생성하는 것으로 다양한 시도를 통해 목표 궤적과의 오차 즉 반응성을 높일 수 있는 특징 벡터를 정의하고자 한다.
본 논문은 다음과 같이 구성된다. 2장에서는 동작 합성 특히 그래프 기반 동작 합성에 관한 관련 연구를 제시하고, 3장에서는 일반적인 모션 매칭 구현에 관한 설명을, 4장에서는 다양한 특징벡터 정의에 따른 오차 분석 결과를 제시한다. 5장에서는 결론을 맺고 향후 과제에 대해 논한다.
2. 관련 연구
이 장에서는 본 연구와 밀접한 관계가 있는 동작 캡처를 통해 획득한 예제 데이터에 기반을 둔 동작 합성 기술 및 모션 매칭 관련 기존 연구 결과에 대해 간략히 기술한다.
예제 동작에 기반을 둔 동작 합성 기술은 그 생성 결과의 사실성으로 인해 동작 포착 기기가 널리 보급된 2000년대 이후 널리 연구되고 개발되고 있는 방법론이다. 기존에 포착된 동작을 그대로 사용하기보다는 사용자의 요구조건 및 환경조건에 맞게 재조정, 재생산하는 것에 초점을 둔 연구 방법들을 위주로 현재까지도 활발하게 연구되고 있다.
특히 2002년도 Arikan et al. 및 Kovar et al., Lee et al. 등이 거의 동시에 발표한 동작 그래프 기반 연구 결과들[1][2][3]은 사용자의 조건에 맞도록 동작의 시퀀스를 재조합하는 방식으로 새로운 동작은 생성하였다. 이러한 동작 그래프 기반의 방법을 적용할 때 결과물에 가장 큰 영향을 주는 요소 중 하나는 연결 가능한 동작 데이터 간의 유사도(또는 거리)를 측정하는 방법이며, 이에 대한 측정 방식이 실세계를 잘 반영하여 직관적이고 타당하여야 예측 가능한 결과 동작들을 생성할 수 있다. Kovar et al.는 [4]에서 큰 동작 데이터에서 연결 가능성을 미리 계산해 놓는 매치 웹(match web) 개념을 발표하면서 이때 자세 간의 유사도를 측정하는 방법의 중요성에 대해서 논하기도 했다.
동작 그래프 기반 기술들은 구현의 간단함과 적용의 유연성으로 인해 다양한 후속 연구들로 연결되었으며, Hyun et al. 의 동작 문법[5] 등의 기술이 있다. 또한 기존의 동작 그래프의 연결 가능 동작은 예제 동작만으로 한정되어 이산적(discrete)인 조합을 통한 연결만이 가능하나 동작 혼합을 기반으로 이를 연속적인 공간으로 확장하고, 강화학습을 통해 연결 동작을 생성하는 동작 장(motion field) 방법으로 발전되었다[6]. 최근 기계 학습 및 생성 모델이 동작 생성에 활발히 적용되면서 그래프 기반 동작 생성 분야에서도 기계학습을 적용한 방법들 또한 많이 발표되고 있다[7][8][9][10].
모션 매칭은 실시간 게임에서의 동작 생성을 위해 동작 장 기술[6]을 간략화하여 Buttner와 Clavet이 2015년 발표하였으며[11], 이어진 2016년 Clavet 및 Zadziuk이 각각 동작 데이터베이스에서 주어진 조건에 맞는 시퀀스를 검색하는 방식으로 GDC에서 발표하였는데[12][13], 검색을 위해 현재의 자세와 미래의 궤적을 비교하는 매우 간단한 방법이지만 자세들을 검색해 이어붙이면서 조정성을 높이고 매우 사실적인 동작을 생성할 수 있음을 보임으로써 많은 주목을 받았으며 이후 게임과 같은 실시간 동작 생성 분야에 활발히 적용되고 있다. Harrow는 UFC와 같은 캐릭터 간 근접 동작 생성에[14], Buttner와 Zinno는 파쿠르 및 축구 게임에서의 동작 생성에 각각 모션 매칭 기술이 잘 적용될 수 있음을 보였다[15][16]. 최근 기계 학습 및 생성 모델을 통한 동작 생성 기술이 각광을 받으면서 모션 매칭에 기계 학습을 도입하고자 하는 연구들도 활발히 연구되어왔다. Holden 등은 모션 매칭의 검색을 통한 생성 방식에서 검색 과정을 미리 학습한 모델로 바꿈으로써 기계 학습 기반의 동작 생성에 모션 매칭이 성공적으로 적용될 수 있음을 보였다[17][18]. 또한 최근 Lee 등은 모션 매칭의 미래 궤적에 대한 검색을 개선한 Long-horizon 모션 매칭 방법을 발표하였다[19].
3. 모션 매칭
모션 매칭은 실세계에서 포착된 동작을 바탕으로 사용자의 입력 조건에 맞도록 동작 시퀀스를 재조합하여 생성하는 기술이다. 실제 동작 포착을 이용하기에 방법에 내재된 매개 변수들을 잘 조정하면 현실적이고 자연스러운 애니메이션을 효율적으로 생성할 수 있다.
모션 매칭의 핵심 아이디어는 먼저 전처리 단계를 통해 주어진 예제 동작 데이터의 각 프레임마다의 자세를 자세 및 궤적을 고려한 간단한 특징 벡터로 변환하고 원 자세 정보와 함께 저장하여 데이터베이스를 구축한 뒤, 온라인 생성 단계에서는 현재의 상태 및 요구조건으로부터 가장 적합한 자세를 데이터베이스에서 검색·선택하는 것이다. 즉 동작의 생성을 자세 데이터베이스의 검색으로 대신하며, 따라서 이 과정에서 효과적인 검색을 위한 검색 쿼리 즉 입출력 특징 벡터의 정의는 효과적인 모션 매칭을 위한 매우 중요한 요소가 된다.
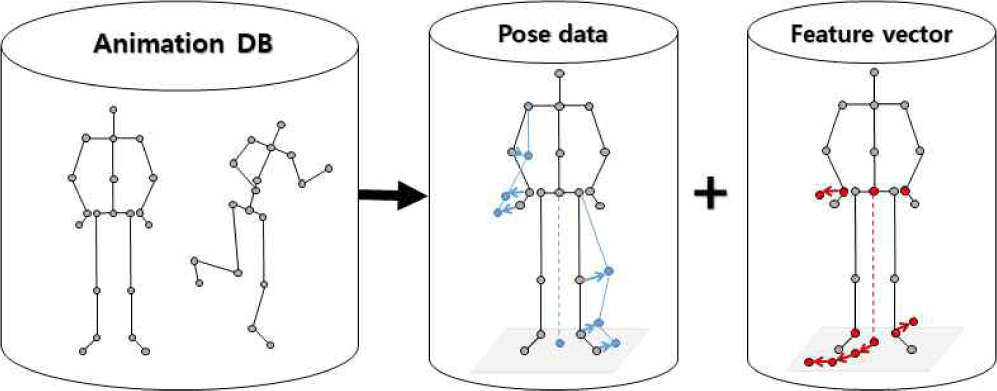
모션 매칭의 전처리 과정인 주어진 동작 데이터로부터의 자세 데이터베이스 구성은 다음과 같은 단계를 거친다. 먼저, 각 프레임의 관절 위치와 회전 정보를 사용하여 임의의 위치 및 방향에서도 자세를 재생성할 수 있는 정보를 구성한다. 이를 위해 첫 번째로, 각 프레임마다 그 당시 뼈대의 루트 관절(root joint)의 위치와 방향을 기준으로 로컬 좌표계를 구성한다. 로컬 좌표계는 루트 관절을 원점으로 하고, 루트 관절의 방향을 기준으로 한 좌표계로, 이를 통해 동작 데이터의 각각의 프레임들의 관절 위치를 상대적 위치로 표현할 수 있다. 두 번째로, 변환된 로컬 좌표계를 사용하여 루트 관절의 궤적 정보를 변환한다. 이때 평면에서의 보행 동작을 가정하며, 따라서 루트 관절의 움직임 중 2차원 평면 위치 및 임의의 방향을 향하는 2차원 회전 정보는 자세의 모양 자체에 영향을 주지 않으며, 자세의 모양에 영향을 주는 것은 루트의 높이 정보(y축으로 가정)와 루트의 y축 회전 방향(roll 회전)을 제외한 2가지 회전 성분(pitch와 yaw)이 된다.
특징 벡터는 위에서 정의된 각 프레임마다의 지역 좌표계에서의 궤적과 뼈대의 주요 끝단(end point)의 위치 정보를 기반으로 정의된다. 궤적 위치와 속도는 캐릭터의 미래 동작 경로를 나타내며, 뼈대의 주요 끝단 위치는 해당 자세를 특징지을 수 있는 가장 중요한 관절들의 위치를 의미한다. 궤적 정보는 입력 궤적을 따라가는 등의 사용자 조작에 알맞은 자세를 고르는 데 역할을 하며, 자세 정보는 자연스럽게 이어지는 동작을 구성하는 데 역할을 한다. 특징 벡터에 자세 정보를 구성하는 모든 관절의 위치 및 방향 정보를 포함할 수 있겠으나, 이는 크기가 커져 오히려 효과적인 검색에 방해가 될 수 있어 최소한의 그러나 자세를 구별할 수 있는 정보만을 담는 것이 중요하다.
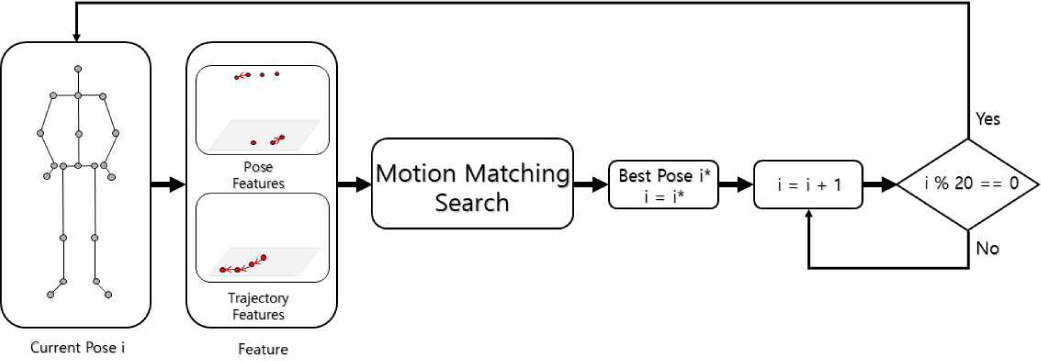
온라인 생성 단계에서는 캐릭터의 현재 상태와 주어진 사용자 조건을 기반으로, 미리 계산된 자세 데이터베이스를 일정한 간격(예: 20프레임 = 0.15초)마다 검색하여 최적의 자세를 찾는다. 이를 위해 모션 매칭 수행 과정을 거치는데, 현재 캐릭터의 자세로부터 특징 벡터를 생성하고, 데이터베이스에서 가장 유사한 자세를 추출한다. 자세 간 유사도를 측정하기 위해 특징 벡터 간의 L2-norm을 사용하였다. 이때, 현재와 동일한 자세가 검출되는 것을 방지하고 다양한 자세를 선택하기 위해 현재 자세와 시간상으로 인접한 k개의 자세는 선택하지 않는다(우리 구현에서는 k=20 프레임으로 설정). 유사도 계산 시 특징벡터 내 자세의 차이와 궤적의 차이의 값의 범위를 맞춰주기 위해 데이터베이스 전체의 자세 벡터의 값의 변화 범위와 궤적 값의 범위를 정규화 시켜주었다.
최적의 자세를 얻은 후에는 현재 자세에서 시작하여 애니메이션을 부드럽게 이어 붙여 나가야 한다. 실제로 동작을 시각화하거나 공간에 배치하기 위해서는 지역 좌표계를 전역 좌표계로 변환해야 하므로, 동작 생성 첫 프레임을 시작으로 각 프레임마다 추가해가는 자세들의 원래의 데이터에서의 앞 프레임과의 루트 관절의 위치 차이 및 방향 차이 값을 생성 동작에 누적해 가는 방식으로 전역 좌표계를 재구성한다.
새로운 자세 시퀀스를 얻을 때, 캐릭터의 자세가 갑작스럽게 변하는 현상이 발생할 수 있다. 이를 방지하기 위해 블렌딩 작업을 수행하여 최종 애니메이션을 부드럽게 다듬는다. 블렌딩은 자세 간의 부드러운 전환을 위해 이어 붙여지는 프레임 간의 자세 차이를 이후 프레임으로 서서히 분산시켜 주는 작업이다[20]. 이를 통해 자세 변화가 자연스럽게 이어져 보다 사실적인 애니메이션을 생성할 수 있다.
4. 실험 및 분석
본 연구는 보행 동작에 집중하여 달리기와 뛰기, 방향 전환 등 다양한 동작으로 구성된 평지 보행 동작을 실험 데이터로 사용하였다. 사용한 데이터는 그림3에서 보이듯 120Hz로 포착된 총 8,171프레임(~68초) 분량의 동작 데이터로 Holden 등이 공개한 데이터이다[21]. 그림4는 이 동작 데이터의 중심 위치로부터 추출한 궤적 데이터를 보여주는데, 정해진 공간 안에서 다양한 곡률 회전 및 속도, 급격한 방향 전환 등이 포함된 데이터임을 보여준다. 본 연구에서는 모션 매칭의 특징 벡터의 다양한 선택에 대한 유효성을 검증하기 위해 우선 Clavet이 처음 발표한 자료[12]를 토대로 윈도우 PC 상에서 C++과 OpenGL을 이용하여 구현하였다.


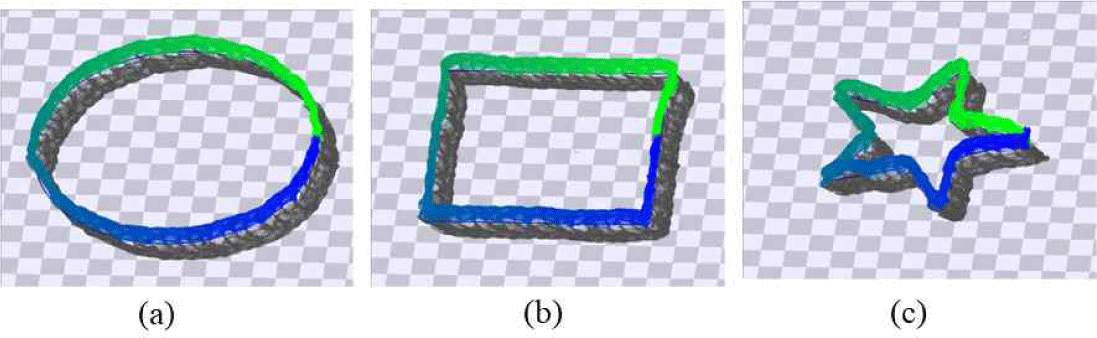
본 연구에서는 특징 벡터의 선택에 따른 생성 동작의 오차를 분석하는 것을 주된 실험의 대상으로 한다. 이를 위해 그림5에서 보이는 것과 같이 3개의 목적 궤적을 미리 정의하고 이를 따라가는 동작을 생성하며 그때 생성된 동작 궤적과의 오차를 측정하고 분석하고자 한다. 목적 궤적은 일정한 곡률을 가지는 원, 비교적 긴 직선과 90도 턴을 포함하는 사각형 모양, 그리고 급격한 턴을 포함하는 별 모양 궤적을 선정하였다.
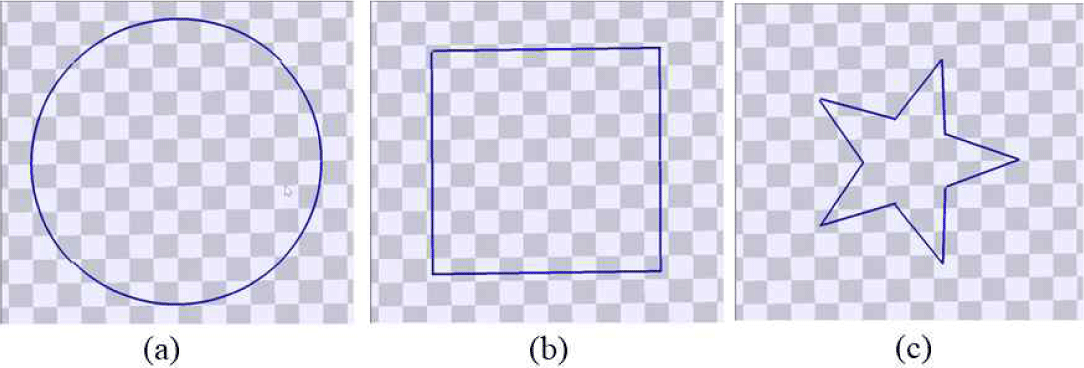
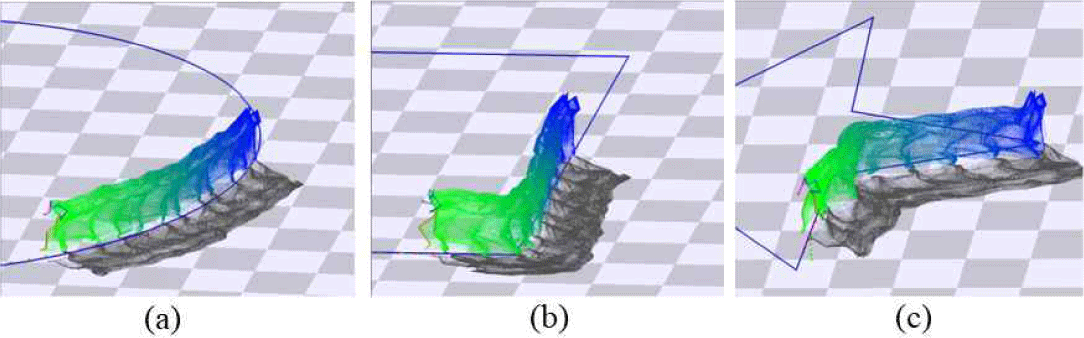
그림 6은 주어진 궤적을 따라가는 생성 결과의 예를 각각 보여준다. 특징 벡터의 선택에 따른 정량적 오차는 생성된 궤적 간의 거리 오차로 계산하였다.
궤적을 잘 따라가게 하기 위한 가장 간단한 특징 벡터로는 각 프레임에서의 예측되는 미래 프레임의 위치를 이용하는 것으로[12], 모션 매칭 시 사용자가 설정한 미래 궤적의 위치와 비교하여 최적의 프레임을 고르는 방식으로 적용될 수 있다. 그러나 이때 어디까지의 미래를 고려할 것인가와, 미래 프레임 중 몇 개를 샘플링하여 고려할 것인가가 주요 결정할 매개변수가 된다(즉 예를 들어 90프레임까지 30프레임 간격으로 고려)(그림 7(a)). 또한 더 부드러운 동작 생성을 위해 과거 지나온 궤적을 함께 고려하는 것도 생각해 볼 수 있다(그림7(b)). 여기에 추가로 목적 궤적의 위치뿐만 아니라, 그때의 속도 또한 같이 고려해 볼 수 있다(그림7(c)). 마지막으로 미래 프레임 중 가까운 프레임의 중요도에 가중치를 주는 방식도 고려해 볼 수 있는데, 이는 강화학습에서 활용되는 가치함수에서의 할인율 개념을 도입한 것으로 모션 매칭이 강화학습 기반의 모션 필드[6]의 간략화된 구현인 점을 고려한 것이다. 이러한 조합에 따라 표1과 같은 실험 종류를 결정하고 각각의 궤적에 따른 오차의 평균 및 표준편차를 계산하였다.
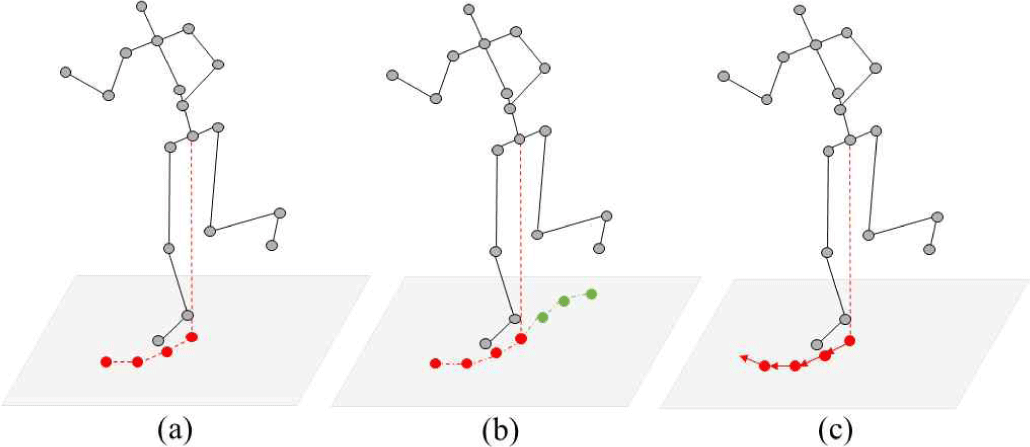
표 1의 케이스 1~7까지는 미래 궤적을 고려할 때 샘플링된 궤적 위치의 개수를 변화하며 오차를 측정한 것이다. 모두 동일한 20프레임씩의 간격으로 샘플링하였으며, 샘플링이 증가할 수로 오차가 줄어드는 경향을 보이다 5개에서 최적의 결과를 보이고, 이후로는 다시 오차가 증가함을 볼 수 있다. 샘플링 개수를 늘릴 때 다시 오차가 증가하는 것은 미래 궤적을 멀리 많이 볼수록 각 샘플의 중요도가 분산되기 때문으로 판단된다. 케이스 8~9는 위에서 얻은 최적의 결과인 “20프레임 씩 5개”에 해당하는 총 100프레임의 시간 동안 서로 다른 간격인 “25프레임씩 4개”와, “33프레임씩 3개”의 경우를 비교한 것으로 25프레임씩 4개가 더 좋은 결과가 나옴을 볼 수 있다.
케이스 10~11은 과거의 궤적까지 고려한 것으로 고려하지 않을 때보다 일괄적으로 더 안 좋은 결과가 나왔다. 이는 과거의 진행 과정이 현재 자세 간의 유사도를 높여 줄 수는 있지만 미래 진행 궤적에는 영향이 적기 때문으로 보인다.
케이스 12~15는 궤적의 속도를 고려하여 특징 벡터를 구성하고 오차를 계산하였다. 이때 위치와 속도의 가중치의 비율을 변화시켜가며 계산하였는데, 위치와 속도의 가중치가 0.8:0.2일 경우가 가장 좋은 결과가 나옴을 알 수 있다. 속도의 가중치가 높아질 수로 결과 궤적의 모양은 유지하나 정확한 위치를 맞추지 못한 경우가 생겼다. 예를 들어 90도 턴이 요구되는 시점에는 정해진 90도 턴을 하나 그 위치가 잘 못 되어도 바로잡는 데 시간이 걸렸다. 위치만을 고려했을 때는 90도 턴의 정확성보다는 다소 둥글게 턴을 하더라도 위치를 최대한 지키는 방향성을 보였다.
케이스 16~19는 각 샘플의 가중치에 할인율을 적용한 것으로 예를 들어 할인율이 γ일 때 i번째 샘플의 가중치는 γi-1이 된다. “25프레임씩 4개”의 샘플링 조건에서 0.7의 할인율일 때 가장 좋은 결과를 나타냈다.
최종적으로 “25프레임씩 4개”의 샘플로 미래 궤적 및 속도를 고려하며, 0.7의 할인율을 적용할 때 대체로 가장 우수한 결과를 보임을 알 수 있었다. 그림 8은 이렇게 얻은 결과 동작을 보여준다.
5. 결론 및 토의
본 연구에서는 최근 실시간 동작 생성에서 많이 활용되고 있는 기술 중 하나인 모션 매칭의 실용성을 높이기 위한 다양한 특징 벡터 설정에 대한 검증을 시행하여 다음과 같은 결과를 얻었다. 일반적인 보행 중심 동작의 경우 100 프레임 (=0.8초) 정도의 미래 궤적을 고려하는 것이 좋으며, 이 경우 4개 정도의 샘플링이 가장 좋은 결과를 나타냄을 알 수 있었다. 과거의 궤적을 같이 고려하는 것은 오히려 오차를 크게 만드는 것 또한 확인하였다. 속도를 같이 고려하는 것은 궤적의 정확도를 높이는 데 기여할 수 있으나, 속도에 대한 가중치를 높이게 되면 생성되는 궤적의 모양은 정확해지나 절대적인 위치에는 오차가 생기게 된다. 강화학습의 할인율의 개념을 도입하는 것 또한 오차를 줄이는 데 도움이 되는 것을 확인하였다.
본 연구는 최대한 다양한 설정으로 실험을 진행하였으나 다음과 같은 한계를 가진다. 먼저 예제 동작에 기반을 둔 방법이라 예제 동작의 종류에 따라 실험 결과가 달라지는 것은 필연적이다. 그러나 보행 동작 일반에 대해서는 미래 궤적의 최적 요구 시간 값은 크게 달라지진 않을 것으로 예측되며 향후 예제 동작을 달리하며 이를 검증할 것이다. 둘째, 같은 파라미터일지라도 궤적의 종류에 따라 오차값은 달라진다. 예를 들어 속도의 가중치를 높이면 원이나 사각형보다는 별 모양의 궤적에서 오차가 커지게 된다. 그러나, 우리 실험에서는 최적의 세팅에서 세 궤적 모두 골고루 가장 좋은 결과값을 보여주었다. 마지막으로 본 실험의 결과를 데이터베이스 검색이 아닌 딥러닝을 통한 생성 모델[18]에 적용했을 때 동일하게 적용될 것인가에 대한 검증이 필요하며 이에 대해서는 향후 검증을 진행해 갈 것이다.









