몬테카를로 방법 기반의 이동최소제곱을 이용한 밀도 데이터의 벡터장 시각화

1 서론

MLS는 분산된 데이터를 부드럽게 근사하거나 고차 보간하기 위 해 사용되는 방법이다. MLS를 확률 밀도 함수에 적용하면 보 다 정확한 확률 분포를 계산할 수 있기 때문에 유체 [1, 2], 변형 체 [3], 메쉬화 [4, 5] 등의 분야에서 활용되고 있다. 다항식 기반 의 보간은 샘플링 지점 사이에서 데이터를 검색하는 데 활용되기 때문에 연속적인 재질의 동적 움직임을 표현하는 유체 시뮬레이 션이나 캐릭터 모델링에서 많이 사용되며, 이 경우 적절한 보간 방법을 선택하는 것은 품질에 영향을 주기 때문에 매우 중요하 다 [6, 7, 8].

보간을 통해 샘플링 데이터를 얻는 과정은 물리 기반 시뮬레 이션에서 중요한 과정이다. 기하학적 처리에서는 포인트 클라우 드 데이터로부터 메쉬표면을 근사 생성하는데 활용되며, 포인트 클라우드는 연결정보가 없기 때문에 고차 수치 방법을 통해 암 시적으로 삼각형 기반으로 구성된 메쉬를 만들어 낸다 [4]. 또한 물리 기반 시뮬레이션 분야에서는 시뮬레이션 정확도를 개선하 기 위해 고차 수치 보간법을 사용한다 [9]. 연기 시뮬레이션의 이류항에 활용되는 선형보간 기반의 세미 라그랑주 방식을 [10] 개선하기 위해 BFECC(Back and forth error compensation and correction) [11], CIP(Constrained interpolation profile) [12], US-CIP(Unsplit semi-Lagrangian CIP) [13], 스트림 기반 연기 [14], 주 파스 기반 연기 [15], 적응형 와류 기법 [16], Polynomial PIC [17] 등 기법들이 제안되었다.

Feldman et al.은 적응형 격자에서 부드러운 벡터장을 얻기 위 해 속도의 정규 성분(Normal component)을 기반으로 MLS를 계 산했다 [18]. MLS는 고차 보간을 위한 기술이며, 앞에서 언급했 듯이 다양한 분야에 활용되지만 MLS의 연속성 조건이나 물리적 제약조건을 만족시키는 것이 어렵기 때문에 시뮬레이션에서는 적극적으로 활용되지 못했다. Hong et al.은 발산제약 기반 MLS 기법을 제안하여 푸아송 방정식을 풀지 않아도 유체와 유사한 움직임을 표현할 수 있는 벡터장 생성 기법을 제안했으며 [6], 이 를 연기 시뮬레이션에 적용하여 복잡한 난류의 움직임을 표현했 다 [7].

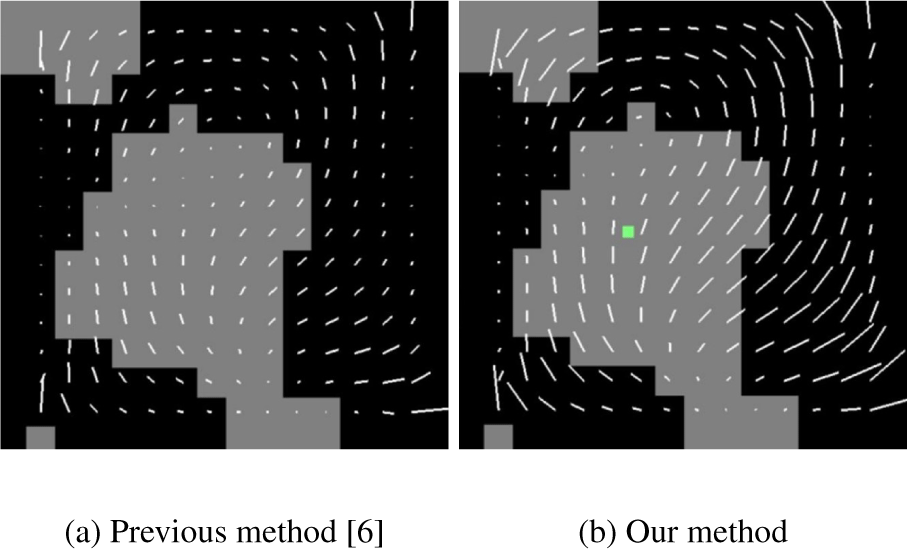
본 논문에서는 밀도를 가진 데이터에서 벡터장을 표현할 수 있 는 방법을 몬테카를로 가중치 기반 MLS 기법을 통해 계산한다. Figure 1은 일반적인 MLS 기법과 Hong et al.이 제안한 발산제약 기반 MLS의 벡터보간 차이를 보여주는 그림이다 [6]. Figure 1a 는 수직으로 마주 보는 두 벡터를 제약조건으로 MLS를 계산한 결과이며, Figure 1b는 발산제약 기반 MLS를 통해 계산된 벡터 장이다. 발산제약 기반 MLS는 유체 시뮬레이션에 적용하기 위 해 비압축성을 보장하는 보간기법이며 (Figure 1b 참조), 그 결 과는 일반적인 MLS와 비교했을 때 명확하게 차이가 나타난다 (Figure 1a 참조). 특히 이 결과는 벡터형태의 제약을 발산 조건에 따라 다르게 표현할 수 있기 때문에 벡터장을 다양한 형태로 디 자인하거나 물리 기반 시뮬레이션에서 활용할 수 있다. 하지만, 제약조건이 벡터로만 표현되기 때문에 밀도를 고려하지 못한다. 밀도는 곧 연기 시뮬레이션에서 중요한 물리적 특성이기 때문에 반드시 고려해야 될 부분이다. 본 논문에서는 몬테카를로법을 활 용하여 밀도가 분포되어 있는 위치를 추정하고, 추정된 위치와 주변 데이터 간의 거리를 MLS의 추가적인 가중치로 활용하여 밀도를 고려한 벡터장을 시각화할 수 있게한다.

Figure 1: Comparing standard MLS vector interpolation to pseudo-divergence-free vector interpolation [6].

Download Original Figure

2 관련 연구

유체 시뮬레이션 분야에서는 난류의 시각적인 디테일을 개선하 기 위해 다양한 종류의 이류 및 외력 기법들이 제안되어 왔다 [19, 20, 10]. 세미 라그랑주 기법은 안정적인 유체를 시뮬레이션하 기 위해 제안되었으며 [10], 와류 제한 기법(Vorticity confinement method)은 격자기반에서 난류를 표현하기 위한 와류 힘을 추정했 으며 [21], 향후 라그랑지안 입자를 와류 운반체로 활용하여 와류 입자 방법(Vortex particle method)으로 개선되었다 [22]. 그 외에 도 BFECC [11], CIP [12], USCIP [13], 스트림 기반 연기 [14], 주 파스 기반 연기 [15], 적응형 와류 기법 [16], Polynomial PIC [17] 등 기법들이 제안되었다.

많은 기법들이 입자 시뮬레이션을 통해 서브그리드 디테일을 강화하려고 노력해왔다. Kim et al. [23]과 Losasso et al. [24]은 서 브그리드 스플래시를 해결하기 위해 SPH(Smoothed particle hydrodynamics)모델을 사용했다. Greenwood와 House [25], Hong et al. [26], Thuerey et al. [27]은 다상 유체를 보다 세밀하게 표현 하기 위해 입자를 활용한 혼합 접근법을 이용했으며, Gao et al.은 라그랑지안 입자를 사용하여 기체의 고속 특징을 포착했다 [28]. 서브그리드 역학에 물리 모델을 도입하면 다상 인터페이스 [29], 화염 [30, 31], 액체의 디테일을 한 층 더 개선시킬 수 있다 [32]. Hong et al.은 푸아송 방정식(Poisson’s equation)을 풀지 않고도 유체의 움직임 표현할 수 있는 발산제약 MLS를 기법을 제안했 다 [6]. 이 기법을 확장하여 연기 시뮬레이션의 이류 과정에 통함 시킴으로써 난류를 표현했다 [7]. 하지만, MLS 기반 난류는 디 테일보다는 노이즈한 움직임이 크기 때문에 시뮬레이션을 제어 하기 어렵게 만들며, 고차 방정식으로 인한 계산양이 매우 크기 때문에 산업에서 활용하기 어려운 접근법이다.

이 외에도 후처리로 유동의 디테일을 향상시키는 접근법들도 있다. 그 중 일부는 웨이블릿 노이즈 [33], 컬 노이즈를 사용하여 저해상도 시뮬레이션을 위한 난류 움직임을 합성했다 [34, 35]. Chu와 Thuerey는 합성곱 신경망을 사용하여 저해상도 유동과고 해상도 유동간의 관계를 학습했다 [36]. Sato et al.은 패치 기반 텍스처 합성을 이용하여 저해상도 흐름에 디테일 난류를 전송 하는 기법을 제안했다 [37]. 최근에 Chen et al.은 연속체 역학을 기반으로 하는 시뮬레이션과 MLS를 이용하여 종이와 유체의 상 호작용과 그로인해 찢김 현상을 표현할 수 있는 통합형 기법을 제시했다 [38]. 이러한 접근법은 그럴듯한 디테일을 합성하지만 노이즈 함수를 사용하면 고해상도 시뮬레이션의 흐름보다 덜 사 실적인 유동이 생성되는 문제가 있다.

본 논문에서 MLS 가중치로 사용하는 몬테카를로 기법을 사 용하고 있지만, 일반적으로 몬테카를로 방법은 다양한 분야에서 샘플링으로 활용되고 있다. Sawhney와 Crane는 격자없이 기하학 적 모델 기반에서 편미분 방정식을 풀 수 있는 몬테카를로 기법을 제시했다 [39]. 최근에는 인공지능을 통해 장면을 3차원으로 복 원하기 위한 접근법에 몬테카를로 기법을 사용되기도 한다 [40].

3 제안하는 프레임워크

본 논문에서 제안하는 몬테카를로 가중치를 이용한 발전제약 기 반 MLS를 설명하기 위해 기본적인 스칼라와 벡터 보간을 위한 MLS를 먼저 설명한다. 그런 다음 ‘몬테카를로 가중치 기반 MLS’ 장에서 몬테카를로 방법을 통해 밀도의 위치를 추정하고 그로부 터 MLS 가중치를 계산할 수 있는 방법을 제안하여 이로부터 벡 터장을 계산한다.

Figure 2는 본 논문에서 제안하는 알고리즘 개요를 보여주는 그림이다. 본 논문에서는 밀도 데이터를 고려하여 벡터장을 시각 화하기 위해 몬테카를로 방법을 이용해 MLS의 가중치를 조절하 는 새로운 기법을 제안한다. 기존의 MLS 방식이 벡터 기반의 제 약조건만 고려하는 한계를 극복하고, 밀도 정보를 활용하여 보다 디테일한 벡터장을 표현할 수 있다는 점이 본 논문의 장점이다.

Figure 2: Algorithm overview of our method.

Download Original Figure

3.2 몬테카를로 가중치를 이용한 발산제약 기반 이 동최소제곱

3.2.1 확산 미분

이번 장에서는 확산 도함수(Diffuse derivatives)와 몬테카를로 가 중치 기반의 MLS 기법에 대해 소개한다. 수식 1을 미분하면 f 의 정확한 미분 값을 얻을 수 있다 (수식 11 참조).

$$\frac{\partial f}{\partial \text{x}}=\frac{\partial {\text{b}}^T}{\partial \text{x}}\text{c}+{\text{b}}^T\frac{\partial \text{c}}{\partial \text{x}}$$

(11)

위 식에서 오른쪽 두번쩨 항은 간단하게 계산될 수 있지만, MLS에 통합하기에는 계산이 복잡해진다. 이 항을 확산 도함수로 교체함으로써 계산 양이 큰 정확한 미분값에 근사치를 효율적으 로 얻을 수 있다 [6] (수식 12 참조).

$$\frac{\partial f}{\partial \text{x}}=\frac{\partial {\text{b}}^T}{\partial \text{x}}\text{c}+{\text{b}}^T\frac{\partial \text{c}}{\partial \text{x}}$$

(12)

확산 도함수를 사용하면 벡터장인 $\nabla \cdot u=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}$ 의 발산은 다음과 같이 근사할 수 있다 (수식 13 참조).

$$\nabla \cdot \text{u}\simeq \frac{\partial {\text{b}}^T}{\partial \text{x}}{\text{c}}_x+\frac{\partial {\text{b}}^T}{\partial y}{\text{c}}_y+\frac{\partial {\text{b}}^T}{\partial z}{\text{c}}_z$$

(13)

3.2.2 발산제약 조건

Huerta et al.은 발산제약 조건인 ∇ · u = σ를 사용하여 σ = 0 으로 비압축성에 대한 정확도를 개선했다 [41]. 본 논문에서는 σ 가 0이 아닌 값을 가질 수 있도록 허용하여 속도 보간에서 발산을 제 어 했다. B_vec에 발산제 약 조건을 추가하려 면 수식 13을 다음과 같이 다시 작성 해야 한다 (수식 14 참조).

$$\nabla \cdot \text{u}\simeq {\text{b}}_{div}^T\left(\text{x}\right)\cdot \text{c}$$

(14)

여기서 b_div는 다음과 같이 계산한다 (수식 15 참조).

$$\begin{array}{ll}{\text{b}}_{div}\left(\text{x}\right)\hfill & =\frac{\partial \left[{\text{b}}^T\left(\text{x}\right)00\right]}{\partial x}+\frac{\partial \left[{\text{0 b}}^T\left(\text{x}\right)0\right]}{\partial y}+\frac{\partial \left[{\text{0 0 b}}^T\left(\text{x}\right)\right]}{\partial z}\hfill \\ \hfill & =\left[\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}00\right]+\left[0\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}0\right]+\left[00\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial z}\right]\hfill \\ \hfill & =\left[\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial x}\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial y}\frac{\partial {\text{b}}^T\left(\text{x}\right)}{\partial z}\right]\hfill \end{array}$$

(15)

b의 편미분은 b의 각 요소를 개별적으로 미분하여 계산한다. 예를 들어, d = 3이고 m = 2인 경우는 다음과 같다 (수식 16 참조).

$$\begin{array}{ll}\frac{\partial \text{b}\left(\text{x}\right)}{\partial x}=\hfill & \left[0,1,0,0,2x,0,0,y,0,z\right]\hfill \\ \frac{\partial \text{b}\left(\text{x}\right)}{\partial y}=\hfill & \left[0,0,1,0,0,2y,0,x,z,0\right]\hfill \\ \frac{\partial \text{b}\left(\text{x}\right)}{\partial z}=\hfill & \left[0,0,0,1,0,0,2z,0,y,x\right]\hfill \end{array}$$

(16)

수식 9에 발산제약 조건인 $b_{div}^T\cdot c=\sigma$를 넣으면 발산제약 기반 MLS를 계산할 수 있다 (수식 17 참조).

$${\text{W}}_{div}\left(\text{x}\right){\text{B}}_{div}{\text{c}}_{vec}\left(\text{x}\right)={\text{W}}_{div}\left(\text{x}\right){\Phi }_{div}$$

(17)

이 방정식은 앞에서 설명한 MLS 방법을 사용하여 계산할 수 있다. 본 논문에서 사용하는 MLS 제약은 다음과 같다 : $W_{div}=\left[\begin{array}{c}{W}_{vec}\\ {\omega }_{div}\end{array}\right],B_{div}=\left[\begin{array}{c}{b}_{vec}\\ {\omega }_{div}\end{array}\right],{\Phi }_{div}=\left[\Phi ,\sigma \right]$. W_div는 (dN + 1) × (dN + 1)크기의 대각행렬이며, B_div는 (dN + 1) × dk크기의 행 렬이고, Φ_div는 ℝ^dN+1크기의 벡터이다.

3.2.3 몬테카를로 기반 가중치

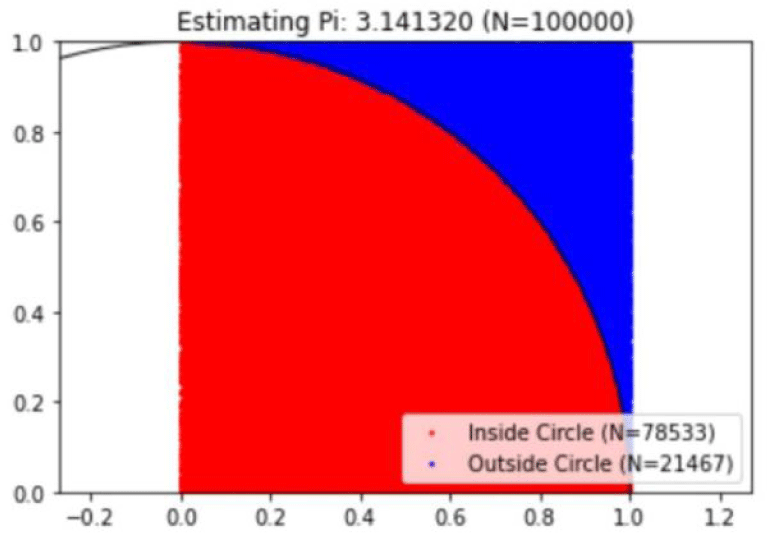
몬테카를로법은 문제를 수치 계산으로 해결하는 대신, 확률적인 난수를 활용하여 근사적으로 해결하는 방법이다. 난수 발생 횟 수의 증가와 균일한 분포 여부에 따라 정확도가 향상되며, 몬테 카를로법을 이용하여 원주율을 계산하는 방법은 가장 간단하고 널리 알려진 예시 중 하나이다.

우선, 하나의 정사각형과 해당 정사각형의 한 변 길이를 $\frac{1}{4}$ 로 하 는 반지름을 가진 원을 그리고, 정사각형 내부에 N 개의 난수를 생성한다 (Figure 3 참조). 이후 원의 중심과각 난수 사이의 거리 를 계산하여 원 내부에 속하는지 여부를 판별한다. 난수가 충분히 생성되었다면, 수식 18과 같은 관계식이 성립한다. 이때 α는 원 내부에 속하는 난수의 개수이며, N 은 전체 난수의 개수이다.

Figure 3: Calculate π with Monte Carlo method.

Download Original Figure

$$\frac{\pi }{4}:1=a:N,\pi =\frac{4a}{N}$$

(18)

본 논문에서는 이미지 내 밀도와 밀집된 위치를 추정하기 위해 몬테카를로법을 사용하며, 이는 원주율을 계산하는 원리와 유사 하다. 수식 19에서 d는 추정하려는 밀도이며, a는 임계값 이상의 밀도를 갖는 영역에 해당하는 난수의 개수를 나타내고, N 은 전체 난수의 개수이다.

$$d:1=a:N,d=\frac{a}{N}$$

(19)

본 논문에서는 효율적인 밀도 검출을 위해 밀도를 먼저 이진 화한다 (이 과정은 선택이며 생략이 가능하다). Figure 4a는 원본 밀도 데이터이며, Figure 4b는 임계값을 0.5로 설정하여 이진화한 결과이다. Figure 4c와 Figure 4d는 각각 1,000개와 100,000개의 난수 샘플을 사용해 밀도를 몬테카를로법으로 추정한 결과이다. 원본 밀도의 평균이 0.3476인 경우, Figure 4c의 추정값은 0.324 로 측정되었고, Figure 4d의 추정값은 0.3452로 계산되었으며, 난 수 샘플 수가 많은 Figure 4d가 더 정확한 근사한 값을 추론하였 다. 이를 바탕으로 이미지 내에서 밀도가 밀집한 위치 추정된다. Figure 4c와 Figure 4d에 나타난 녹색 지점은 추정된 밀도의 밀집 위치를 나타낸다. Figure 4c의 경우 밀집 지역은 각 시뮬레이션마 다 약간씩 다르게 나타났지만, Figure 4d는 거의 일정한 결과를 보여주었다.

Figure 4: Calculate densely location with Monte Carlo method.

Download Original Figure

몬테카를로법으로 계산된 밀도의 밀집 위치와 각 제약 노드 간의 거리를 계산하고, 제약 노드의 결과를 0∼1 범위로 정규화 한다. 몬테카를로법을 통해 MLS 가중치인 ω* (|r_i|)를 구성하는 방법은 다음과 같다 (수식 20 참조).

$$\omega *\left(\left|{\text{r}}_i\right|\right)=\omega \left(\left|{\text{r}}_i\right|\right)\left(q_i-\text{x}\right)$$

(20)

여기서 ω (|r_i|)는 노드와 제약 노드 간의 거리를 계산한 가중치 이고, (q_i − x)는 노드와 몬테카를로법으로 추정한 밀도의 밀집 위치 사이의 거리이며, 이 값을 통해 가중치 행렬인 W를 구성하 여 MLS를 계산한다.

4 실험 결과

본 연구의 결과들을 만들기 위해 실험한 환경은 Intel Core i7-7700K CPU, 32GB RAM, Geforce GTX 1080Ti GPU가 탑재된 컴퓨터를 이용하였다. 본 논문에서 보여주는 결과는 2차원 밀도 맵을 가진 데이터를 통해 벡터장을 표현했다.

Figure 5는 제약 노드를 가지는 장면에서 벡터장을 추 출한 결과이다. Figure 5a는 4개의 각 코너에 제약노드를 가지며 (p1(0.0558, -0.9984),p2(-0.4041, 0.9147),p3(-0.6049, - 0.7962),p4(-0.7164, 0.6976)), 이전 기법인 발산제약 MLS를 통해 계산된 벡터장이다. 이전 기법에서는 밀도 데이터의 특성을 고려 하지 못하고, 제약 노드의 방향만 고려한 벡터장이 나타나는 것을 볼 수 있다. Figures 5b는 앞의 결과와 같은 조건에서 몬테카를로 가중치를 추가하여 MLS를 계산한 결과이다. 같은 제약 노드 환 경임에도 불구하고 Figures 5a의 결과와는 다르게 제약 노드의 형태를 유지하면서 밀도의 밀집 위치를 기반으로 벡터장의 흐름 이 디테일하게 표현되었다.

Figure 5: Comparison of vector field results generated by the previous method and our method.

Download Original Figure

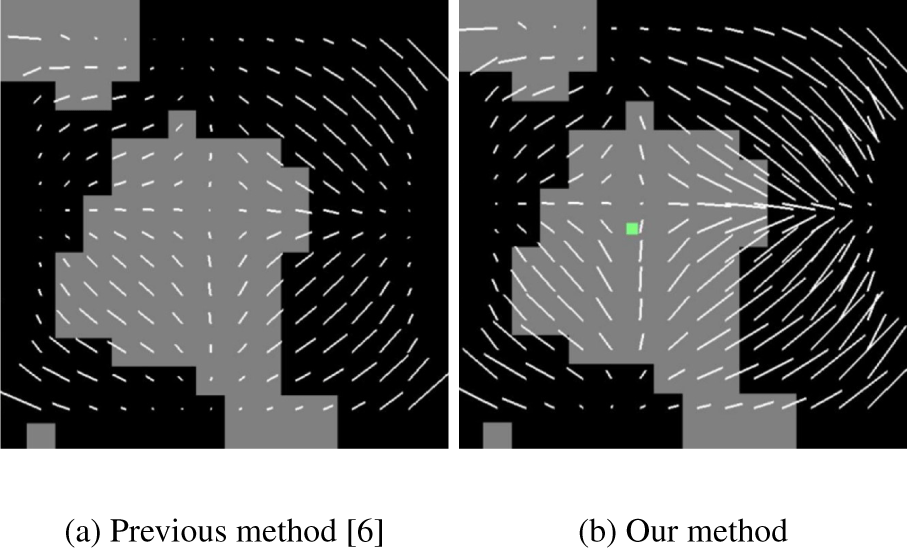
Figure 6은 Figure 5와는 다른 제약 노드로 실험한 결과이 다 (p1(0.9177, 0.397), p2(0.9386, -0.3448), p3(0.2805, -0.9598), p4(0.9249, 0.3802)). 이전 기법에서는 제약 노드에 영향을 받기 때문에 발산제약 MLS임에도 불구하고 벡터장의 크기가 작아 거 의 표현되지 않는 경우도 있지만, 제안하는 방법은 밀도가 큰 영 역을 중심으로 와류가 소실되지 않고 명확하게 표현되었다.

Figure 6: Comparison of vector field results generated by the previous method and our method (constrained nodes.

Download Original Figure

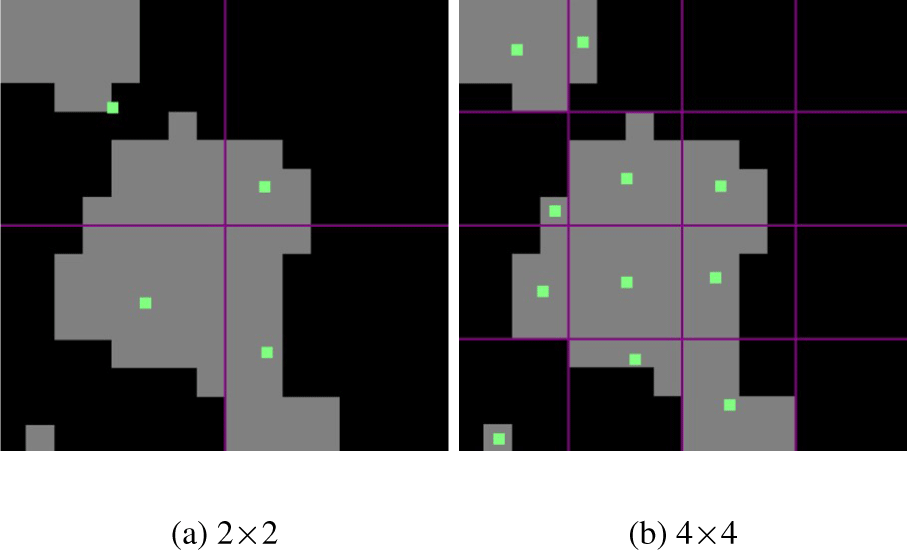
앞에서 보여준 결과들은 밀도의 밀집 위치가 하나로 표현되기 때문에 밀도의 특징을 온전히 고려하기에는 부족하다. 이를 효율 적으로 처리하기 위해 본 논문에서는 밀도를 다루는 공간을 격 자로 분할하여 격자마다 몬테카를로 가중치를 계산하도록 했다. Figure 7은 분할된 격자마다 계산된 밀도의 밀집 위치를 보여주고 있다. 앞에서 보여준 결과와 다르게 격자 분할 해상도가 높을수록 밀도의 밀집 위치가 정확하게 추론되는 것을 볼 수 있다.

Figure 7: Grid partitioning scheme for Monte Carlo weight control.

Download Original Figure

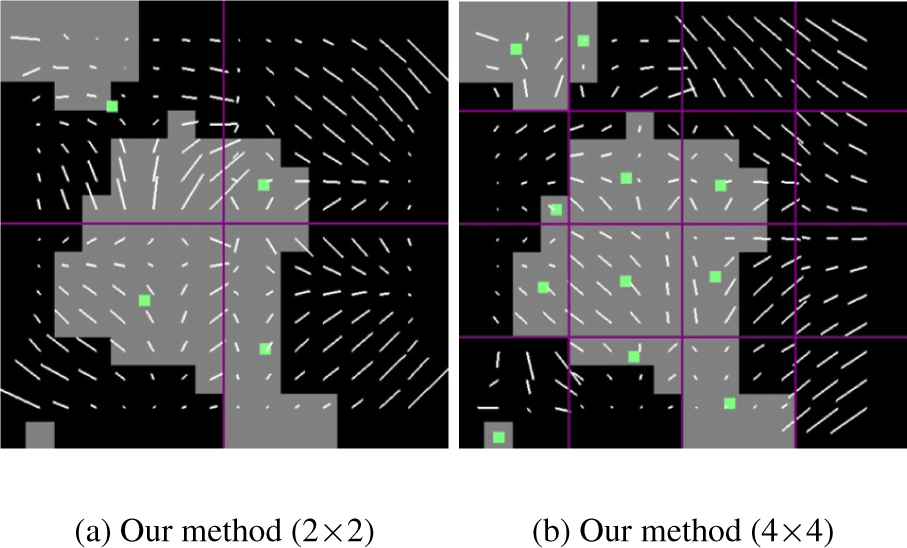
Figure 8은 다양한 격자 해상도를 통해 몬테카를로 가중 치 MLS를 계산한 결과이다 (p1(0.0558, -0.9984), p2(-0.4041, 0.9147), p3(-0.6049, -0.7962), p4(-0.7164, 0.6976)). 몬테카를로 부터 밀도의 밀집 위치가 여러 개가 나올 수 있고, MLS에 필요한 가중치는 노드 위치에 해당하는 밀도의 밀집 위치를 이용하였다. 같은 장면인 Figure 5와 비교했을 때 제안하는 기법은 밀도의 형 태에 따라 와류 및 벡터장의 흐름을 디테일하게 잘 표현했다.

Figure 8: Generation of vector field with our method.

Download Original Figure

5 결론 및 향후 연구

본 논문에서는 밀도의 분포를 고려하여 MLS기반으로 벡터장을 생성하는 새로운 방식을 제안했다. 격자 내 밀도 분포를 효율적 으로 추론하기 위해 입자 기반의 몬테카를로 시뮬레이션 기법을 도입했으며, 이로 인해 격자 해상도를 증가시키지 않고도 디테일 한 벡터장을 계산했다. 하지만 정규격자로 분할하여 밀도의 밀집 위치를 계산하기 때문에 밀도가 고르게 분포되어 있지 않을 경우 에는 약간의 오차가 발생한다. 향후 이 문제를 효율적으로 해결 하기 위해 쿼드트리(Quadtree) 기반의 적응형 공간 분할 기법을 이용하여 알고리즘을 개선할 계획이다. 또한 격자 내 표현되는 서브그리드(Subgrid) 디테일을 개선하기 위해 세미 라그랑주 방 식을 몬테카를로 기반 MLS와 통합하여 디테일하게 연기와 불 의 비주얼 시뮬레이션을 개선시킬 계획이다. 본 논문에서는 입력 데이터가 밀도 이미지이지만, 시뮬레이션에서는 연속적인 밀도 데이터를 이용하기 때문에 시간에 따른 연속성이 보장되어야 하 며, 그렇지 않을 경우 깜빡이는 노이즈 문제가 발생할 수 있다. 향후 위에서 언급한 문제들을 개선시킬 수 있도록 연구를 확장할 계획이다.