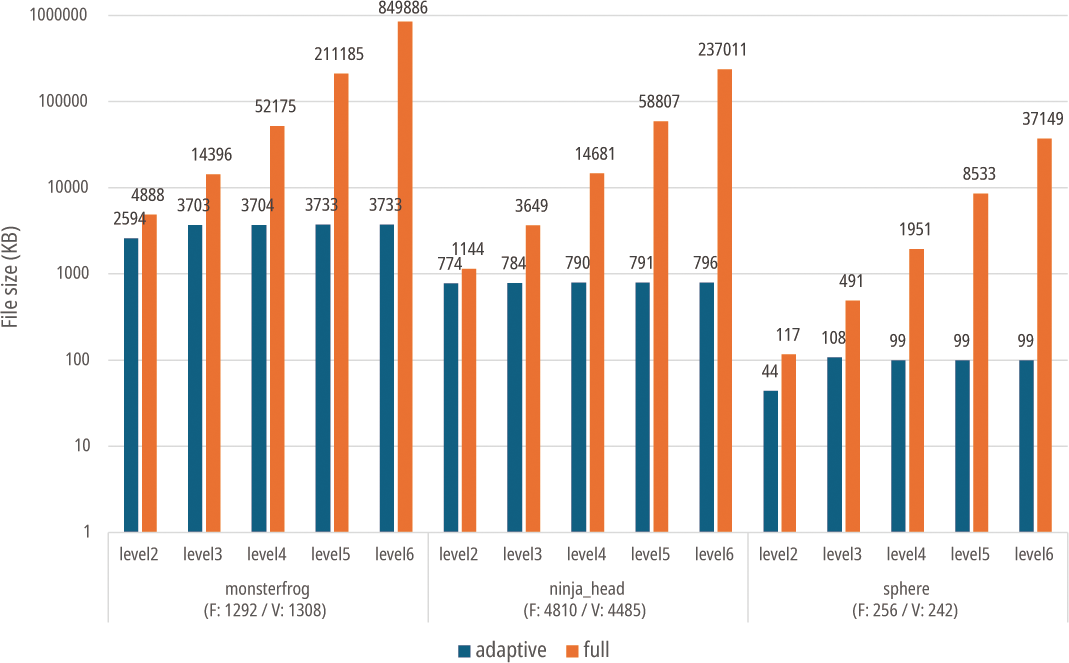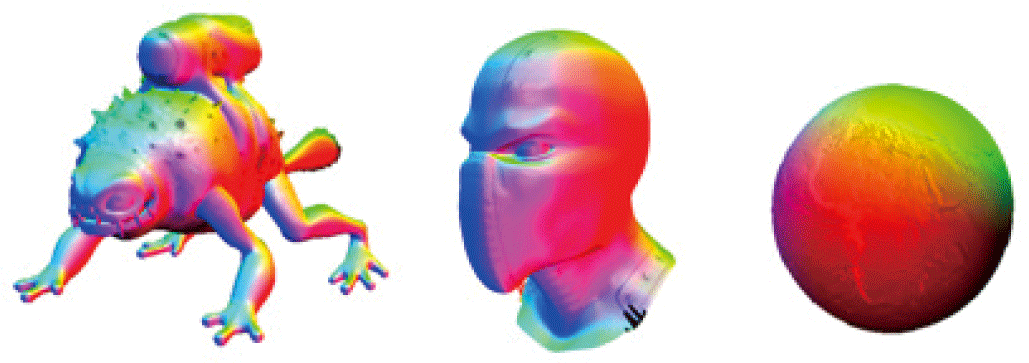1. 서론
실시간 렌더링 기술은 게임, 가상현실(VR) 등 다양한 분야에 서 중요한 역할을 하며, 최근에는 웹 환경으로도 그 활용이 확대 되고 있다. 실시간 렌더링에서 GPU의 병렬 연산을 이용한 작업 분산은 렌더링 효율성을 향상시키고, 서브디비전 기법은 낮은 해 상도의 입력 모델을 부드럽고 정교한 곡면으로 변환해 렌더링을 가능하게 한다. 서브디비전 기법 중 CC 서브디비전은 3D 모델에 서 널리 사용되는 사각형 기반 메시에서 높은 성능을 발휘할 수 있어, 고품질 3D 모델링 및 렌더링에 널리 활용된다.
데스크탑 환경에서는 테셀레이션 셰이더(tessellation shader) 와 같은 하드웨어 기능을 통해 서브디비전 기반 렌더링이 효율 적으로 구현될 수 있으나, 웹 환경에서는 웹 기반 그래픽스 API 인 WebGL로는 그래픽스 하드웨어의 연산 성능을 충분히 활용 하기 어려웠다. WebGL의 근본적인 한계를 극복하기 위해 최근 WebGPU API가 개발되었으며 2023년부터 주요 브라우저에서 정식 지원되기 시작하였고 [3], 웹에서도 향상된 병렬 처리와 하 드웨어 접근성을 제공한다.
본 연구는 WebGPU를 활용하여 텍스쳐 매핑을 지원하는 CC 서브디비전 기반의 실시간 렌더링 기법을 구현하고, 웹 환경에서 데스크탑 수준의 고품질 서브디비전 서피스를 렌더링 하는 것을 목표로 한다. (Figure 1)

2. 관련 연구
최근 연구들은 GPU 기반 연산 환경에서의 서브디비전 효율 을 높이기 위해 서브디비전 과정을 수학적으로 단순화하거나, 메 시 위상 구조에 기반한 병렬 처리 기법을 통해 성능 및 확장성을 크게 개선하였다. Nießner등은 CC 서브디비전 서피스의 효율적 인 실시간 렌더링을 위한 특징-적응형(feature-adaptive) GPU 렌 더링 기법을 제안하였다[1]. 이 기법은 곡면의 기하학적 특성에 따라 서브디비전 레벨을 선택적으로 조정한다. 모델을 렌더링 하 기 전 CPU에서 서브디비전에 필요한 영역을 선별하고 해당 영역 의 위상 정보를 포함하는 서브디비전 테이블(subdivision table)을 생성한다. 이를 통해 GPU에서의 병렬 처리에 최적화된 연산을 가능하게 하였으며, 모든 메시에 서브디비전을 적용하는 방법에 비해 현저한 성능 향상을 달성하였다. Pixar의 OpenSubdiv[4]는 Nießner의 기법을 기반으로 개발된 서브디비전 프레임워크로, 다 양한 그래픽 API 환경에서 실시간 렌더링 환경에서도 부드러운 곡면 표현을 가능하게 한다. Mlakar는 CC 서브디비전을 선형대 수적으로 추상화하여 병렬 구현이 가능함을 보였다. CC 서브디 비전으로 생성되는 메시 구조의 특성을 활용해 행렬곱과 같은 선 형대수적 연산을 특화 커널(specialized kernels)로 대체함으로써 성능과 메모리 효율을 크게 향상시켰다[5]. Dupuy는 CC 서브디 비전의 하프엣지 세분 규칙(halfedge refinement rule)을 단순한 대수 연산으로 정식화하고, 이를 통해 정점 계산을 간소화하며 GPU에서 병렬 처리가 가능한 방법을 제안하였다[6].
디스플레이스먼트 매핑(displacement mapping)을 적용할 때, 텍스처 심(texture seam)에 위치한 정점이 복수의 텍스처 값을 참 조하게 되면서 미세한 값 차이로 인해 크랙(crack)이 발생할 수 있고, 이와 같은 문제를 해결하기 위해 다양한 접근 방식이 제 안되어 왔다. Francisco와 Gustavo는 traveler’s map과 sewing the seams기법을 제시하였다[7]. traveler’s map은 텍스처 차트 간의 대응 관계를 정의하는 양방향 매핑 구조로, 심을 넘나들며 텍스처 값에 접근할 수 있게 한다. 이를 바탕으로 sewing the seams기법은 텍스처가 맞닿는 경계 주변에 보간 삼각형(interpolating triangles) 을 생성하고 이 내부의 값을 통일하는 방식으로 텍스처 값의 불 일치를 보정한다. 이 기법은 텍스처 공간에서만 연산이 이루어 지며 기존 3D 메시의 기하 정보를 변경하지 않는다. Dominant UV 기법은 하나의 정점이 여러 UV 좌표를 갖는 경우, 그 중 하 나를 선택하여 고정하는 방식이다[8]. 구현이 간단하다는 장점이 있으나 디테일 손실이 발생할 수 있는 단점도 존재한다. Songrun 등이 제안한 방법은 고정된 메시를 기반으로, 심이 존재하지 않 는 텍스처 부분을 선형 연산의 영공간(null space)으로 정의하고, 기하적 조건에 따라 심에 해당하는 텍스처 값을 제거하는 방식으 로 고품질의 결과를 도출할 수 있다[9]. 그러나 텍스처 해상도가 낮거나 파라미터화된 심이 서로 근접한 경우, 불연속을 제거하는 과정에서 서로 다른 구조를 병합하거나 세부 표현을 손상시킬 수 있는 한계가 존재한다. 한편, Ptex는 정점(vertex) 단위가 아닌 면 (face) 단위로 텍스처를 할당함으로써, 하나의 정점이 복수의 값 을 갖는 문제를 근본적으로 제거하는 방법이다[10]. 그러나 기존 UV 기반 파이프라인과 호환되지 않는 경우가 많고 실시간 렌더 링에서의 사용이 제한적이라는 단점이 있다.
3. 이론적 배경
본 장에서는 WebGPU API와 3차 B-스플라인 패치, CC 서브디 비전에 대해 간략히 소개한다.
30년이 넘은 OpenGL API를 기반으로 설계된 WebGL은 최신 그래픽스 하드웨어의 성능을 온전히 활용하는 데 근본적인 한계 를 가진다. 이러한 한계를 극복하기 위해 WebGL에 비해 여러 사 항이 개선된 차세대 API로 WebGPU가 개발되었다. WebGPU는 낮은 수준의 하드웨어 접근이 가능해 더 세밀한 성능 최적화가 가능한데 이는 GPU의 내부 동작을 더 잘 제어할 수 있음을 의미 하며 고성능 그래픽 및 컴퓨팅 작업에서 중요한 장점으로 작용 한다. 또한 WebGPU는 WebGL과 달리 GPU 범용 계산(GPGPU: General-Purpose computing on Graphics Processing Units)을 위 한 컴퓨트 쉐이더를 지원하여 복잡한 범용 계산 작업을 병렬로 처리할 수 있어 GPU의 연산 능력을 극대화할 수 있다. 그러나 WebGPU는 데스크탑 그래픽스 API인 Vulkan, DirectX, Metal 등 과 비교했을 때 여전히 미흡한 부분 또한 존재한다. WebGPU는 웹 브라우저 내에서 실행되기 때문에, 리소스 제한, 보안 정책과 같은 브라우저의 제약에 의해 성능 저하가 일어날 수 있고 지원 여부가 브라우저마다 상이할 수 있어 호환성 문제가 발생할 수 있다. 그 외에 멀티 GPU 지원이나, 고급 텍스처 처리 방식 등은 아직 데스크탑 API에 비해 제한적이다.
B-스플라인은 주어진 제어점들을 기반으로 기저 함수(basis function)들의 가중합으로 곡선을 정의하는 방법이다. 이를 이용 한 3차 B-스플라인(bicubic B-spline) 패치는 인접한 4 × 4개의 제어점으로 하나의 패치를 구성한다. 이는 2차원 매개변수 공간 (u, v) 상에서의 곡면 함수로 해석되고 해당 패치의 한 점 S(u, v) 는 다음과 같이 정의된다:
위에서 {Pi,j}0≤i,j≤3는 제어점, {Bi(u)}0≤i≤3는 아래와 같이 정 의된 B-스플라인 기저 함수이다. (t ∈ [0, 1])
각 기저 함수는 특정 구간에서만 유효한 함수로, 기저 함수로부터 생성되는 패치는 일부 제어점의 변화에만 국소적으로(locally)하 게 반응하며, 인접하지 않은 다른 패치들에게 영향을 끼치지 않 는다. 이와 같은 특성으로 인해 B-스플라인 패치는 정규적이고 균일한 메시 구조에서 효율적이고 안정적인 곡면 표현 방식으로 작동한다.
B-스플라인의 서브디비전은 제어 메시(control mesh)에 새로 운 제어점을 추가함으로써 제어 메시의 해상도를 점진적으로 높 이는 방법이다[11]. 서브디비전을 반복하면 해상도가 높아지면 서 곡면으로 수렴하는 새로운 제어 메시가 생성된다. B-스플라인 의 서브디비전은 곡면을 잘게 나눈 여러조각으로 분해하는 것과 동일한 효과를 가지며, 이로 인해 곡면 전체를 고해상도의 제어 메시로로 대체할 수 있게 된다.
서브디비전 서피스(subdivision surface)는 3D 모델의 면 구조 를 반복적으로 분할하여 부드러운 곡면으로 수렴시키는 기법이 다. 이 방식은 낮은 해상도의 입력 메시를 기반으로 연속적이고 고품질의 곡면 표현이 가능하다는 장점이 있다. 이를 무한히 적 용할 경우, 메시의 각 정점은 특정 위치로 수렴하게 되며, 이를 리밋 포지션(limit position)이라 하고 분할된 제어 메시가 수렴하 는 곡면은 리밋 서피스(limit surface)라 한다.
그 중에서도 CC 서브디비전은 임의의 다각형 메시에 적용 가 능한 서브디비전 기법으로, 기존 메시의 면, 엣지, 정점 정보를 기반으로 각 서브디비전 단계마다 세 가지 유형의 점–면, 엣지, 정점 포인트–을 아래 순서로 새롭게 정의하고, 이를 기반으로 메 시를 분할한다.
-
면 포인트는 해당 면를 구성하는 모든 정점들의 평균으로 계산된다.
-
엣지 포인트는 엣지의 양 끝 정점 v1, v2 와 그 엣지를 포함하 는 두 면의 면 포인트 F1, F2를 평균낸 값이다.
-
정점 포인트는 기존 정점의 위치 v, 인접 면 포인트들의 평균 F, 인접 엣지 포인트들의 평균 E를 이용하여 다음과 같이 계산된다.
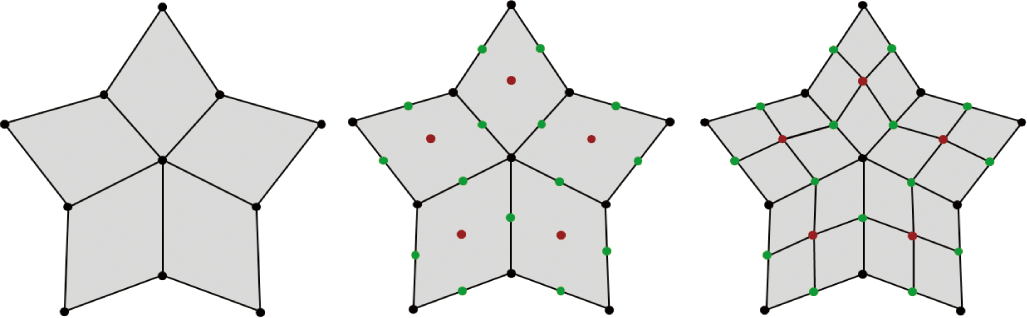
새로운 정점이 생성된 후 1개의 정점 포인트, 2개의 엣지 포인 트, 1개의 면 포인트로 이루어진 새로운 면이 메시에 추가된다. (Figure 2)
CC 서브디비전 서피스는 3차 B-스플라인 패치를 임의의 다각 형 메시(polygonal mesh)로 일반화한 방식이라 할 수 있다. 즉, 정 규 사각형 영역(regular quad region)에서는 해당 곡면이 정확히 3차 B-스플라인 패치로 표현되며, 리밋 포지션과 리밋 법선 벡 터를 계산할 수 있다. 반면, 모델 경계 혹은 차수(valence)가 4가 아닌 정점에 인접한 비정규 영역(irregular region)의 사각면은 B-스플라인 패치로 나타낼 수가 없으므로 반복적인 서브디비전을 통해 리밋 서피스(limit surface)에 수렴하도록 곡면을 단계적으 로 생성해야 한다.
CC 서브디비전의 경우, 정점이 수렴하게 되는 리밋 포지션 P∞는 중심 정점 v, 인접 엣지 중심점의 합 Σjej, 면 중심점의 합 Σjfj, 그리고 차수 n에 기반하여 다음과 같이 계산된다[12]:
이 수식은 해당 정점의 기하학적 이웃들과의 관계를 수치적으 로 반영하며, 반복 연산 없이도 정점의 수렴 좌표를 직접 계산할 수 있게 해준다. 특히 정규 사각형 영역에서는 B-스플라인 패치를 활용하여 리밋 포지션으로 곧바로 렌더링할 수 있다. 리밋 포지 션과 더불어, 곡면의 방향성을 나타내는 리밋 노멀(limit normal) N∞ 역시 주변 정점 정보를 기반으로 계산된다.
위에서 c2와 c3는 다음과 같이 정의된다.
즉, 중심 정점을 기준으로 주변 정점 vi들을 이차원 파라미터 공간 내에서 접벡터(tangent vector)로 해석한 뒤, 그 외적을 통해 법선 벡터를 얻는다. 이러한 계산을 통해 얻어진 리밋 포지션과 리밋 노멀은 B-스플라인 패치 기반의 연산 결과와 시각적으로 매끄럽 게 연결되며, 패치 간의 정합성을 유지하는 데 핵심적인 역할을 한다.
텍스처 심은 서로 다른 텍스처 차트가 맞닿는 경계선이다. 텍스 처 파라미터화(parameterization) 과정에서는 3D 모델의 표면을 2D 텍스처 공간에 매핑하는 과정에서 표면을 여러 차트(chart) 로 나누어 2차원 텍스처 공간에 매핑하는데, 이로 인해 경계 상 의 점이 서로 다른 텍스처 좌표를 가질 수 있다. 색상이나 노멀 텍스처를 적용할 경우 참조한 텍스처 값이 불연속적이더라도 육 안으로는 확인하기 어렵지만, 디스플레이스먼트 매핑의 경우 텍 스처 좌표의 값을 기반으로 해당 정점의 위치를 수정하기 때문에 텍스처 심에서 크랙이 발생할 수 있고 이는 미세한 차이더라도 시각적으로 두드러지기 때문에 문제가 된다.
4. 연구 내용
CC 서브디비전 방식은 모든 영역에 대해 반복적인 서브디비전 연산을 요구하기 때문에, 실시간 렌더링 환경에서는 계산 비용 증가와 성능 저하의 원인이 될 수 있다. 이를 완화하기 위해 정규 사각형 영역은 서브디비전 과정을 반복하는 대신 B-스플라인 패 치로 연산하여 리밋 포지션 및 노멀을 계산할 수 있다. (Figure 1) 실제로 대부분의 사각형 기반 3D 모델은 다수의 면이 정규 사각 형으로 되어있고, B-스플라인 패치는 외부 패치에 영향을 주지 않아 의존성이 없기에 병렬로 연산을 시행할 수 있다. 이는 서 브디비전 과정을 단순화하고 렌더링 성능을 크게 향상시키는 데 기여한다. 단, 정규 영역(B-스플라인 기반 패치)과 비정규 영역 (서브디비전을 적용하는 패치)이 맞닿는 경계에서는 수치적 불 연속으로 인해 Figure 4와 같이 크랙이 발생할 수 있으므로, 두 방식 간의 위치 및 노멀 연산이 시각적으로 매끄럽게 이어지도록 정합성을 유지하는 추가적인 보정 처리가 필요하다.
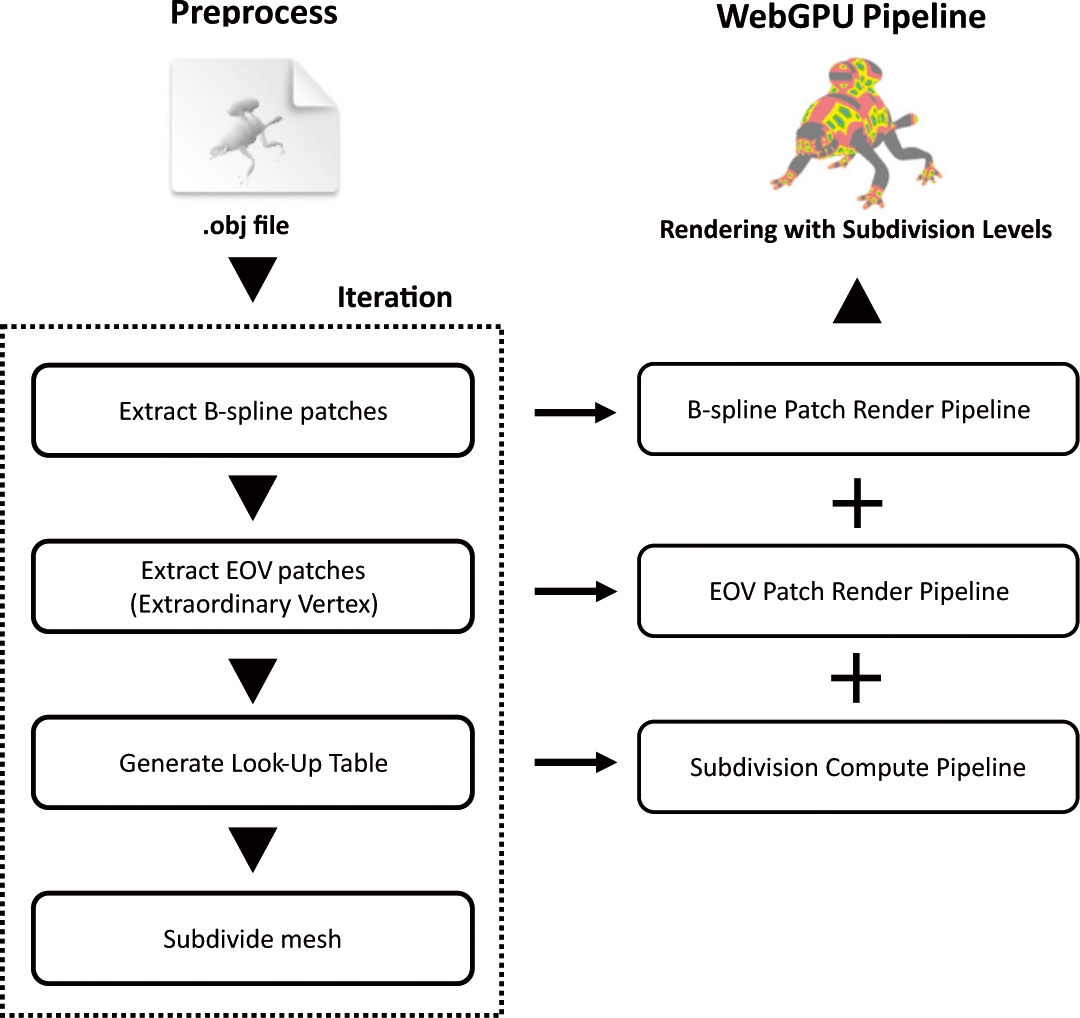
실제로 구현은 Figure 3과 같이, C++ 스크립트 전처리를 하는 과정과 WebGPU에서 렌더링을 하는 과정으로 이루어져 있다. 본 장에서는 먼저 전처리 단계를 통해 메시를 분할하고 정규 사각형 영역과 비정규 영역을 분류하는 방식(4.1)을 소개한 뒤, WebGPU 에서 수행되는 서브디비전 연산(4.2), B-스플라인 연산(4.3), 리 밋 포지션(4.4), 텍스처 매핑(4.5)의 세부 구현 구조를 순차적으로 기술한다.
전처리 단계에서는 모델의 연결 상태를 분석하여 정규영역과 비정규영역을 구분한다. 정규영역에서는 각 면을 구성하는 패치 마다의 제어점의 인덱스(index), 텍스처 좌표값들을 취합하여 저 장한다. 비정규영역에서는 우선 리밋 포지션과 리밋 노멀을 계 산하기 위해 필요한 정점 정보들을 저장한다. 이후 CC 서브디 비전을 수행하며 GPU에서 병렬로 서브디비전을 수행하기 위한 서브디비전 테이블을 생성한다. 위 과정을 서브디비전된 비정규 영역에 대해 반복한다.
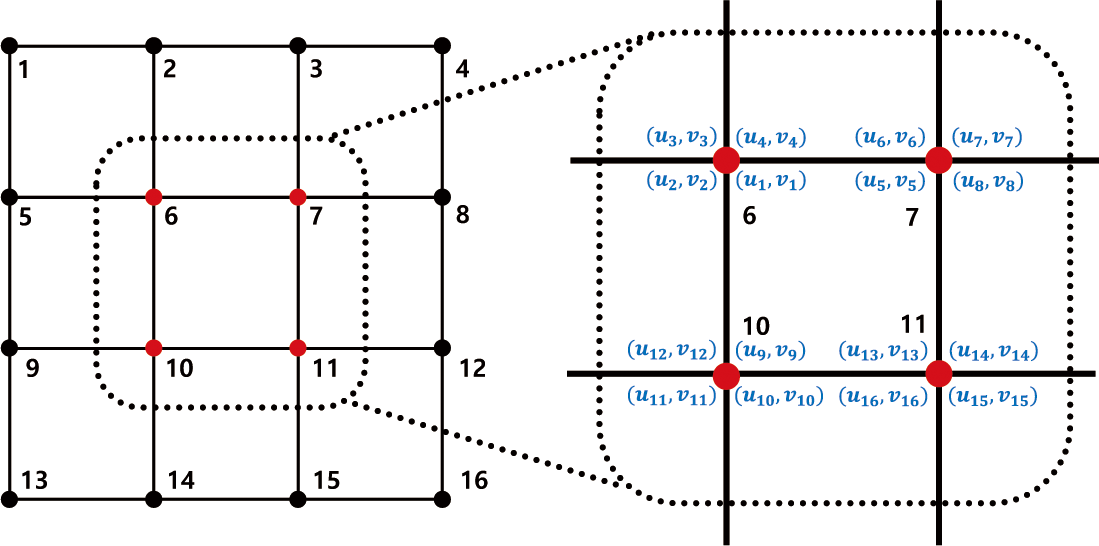
텍스처 매핑 적용시, 서로 다른 서브디비전 깊이를 가진 패치가 만나는 경계 혹은 텍스처 심에서 Figure 4과 같이 크랙이 발생할 수 있다. 이러한 크랙을 해결하기 위해 전처리 단계에서 Figure 5 와 같이 각 패치의 16개의 제어점 인덱스뿐만 아니라 제어점 중 5번, 6번, 9번, 10번에 해당하는 정규 정점들이 가질 수 있는 4개 의 텍스처 좌표를 함께 넘겨준다. 이를 통해 각 패치에 대해 총 16개의 텍스처 좌표를 포함한 정보를 전달함으로써 크랙 현상을 방지할 수 있다.

본 단계에서는 Figure 6과 같이 비정규 영역에 대해서만 CC 서브디비전을 적용한다. CC 서브디비전 연산은 면, 엣지, 정점 포인트를 각각 계산하는 세 단계로 구성된다. 각 단계는 3.3에서 설명한 방식에 따라 병렬 처리가 가능하도록 컴퓨트 쉐이더 모 듈로 구현하였고 정점 정보, 인덱스 정보, 오프셋, 연결된 점들의 수 등을 스토리지 버퍼에 저장하여 효율적으로 데이터 관리가 이 루어진다. 이러한 구조는 GPU 메모리 내에서 빠르고 효율적인 데이터 접근을 가능하게 하여, WebGPU의 효율성을 최대한 활용 하고 계산 자원을 절약하며 동시에 고속의 연산 성능을 제공할 수 있도록 하였다.
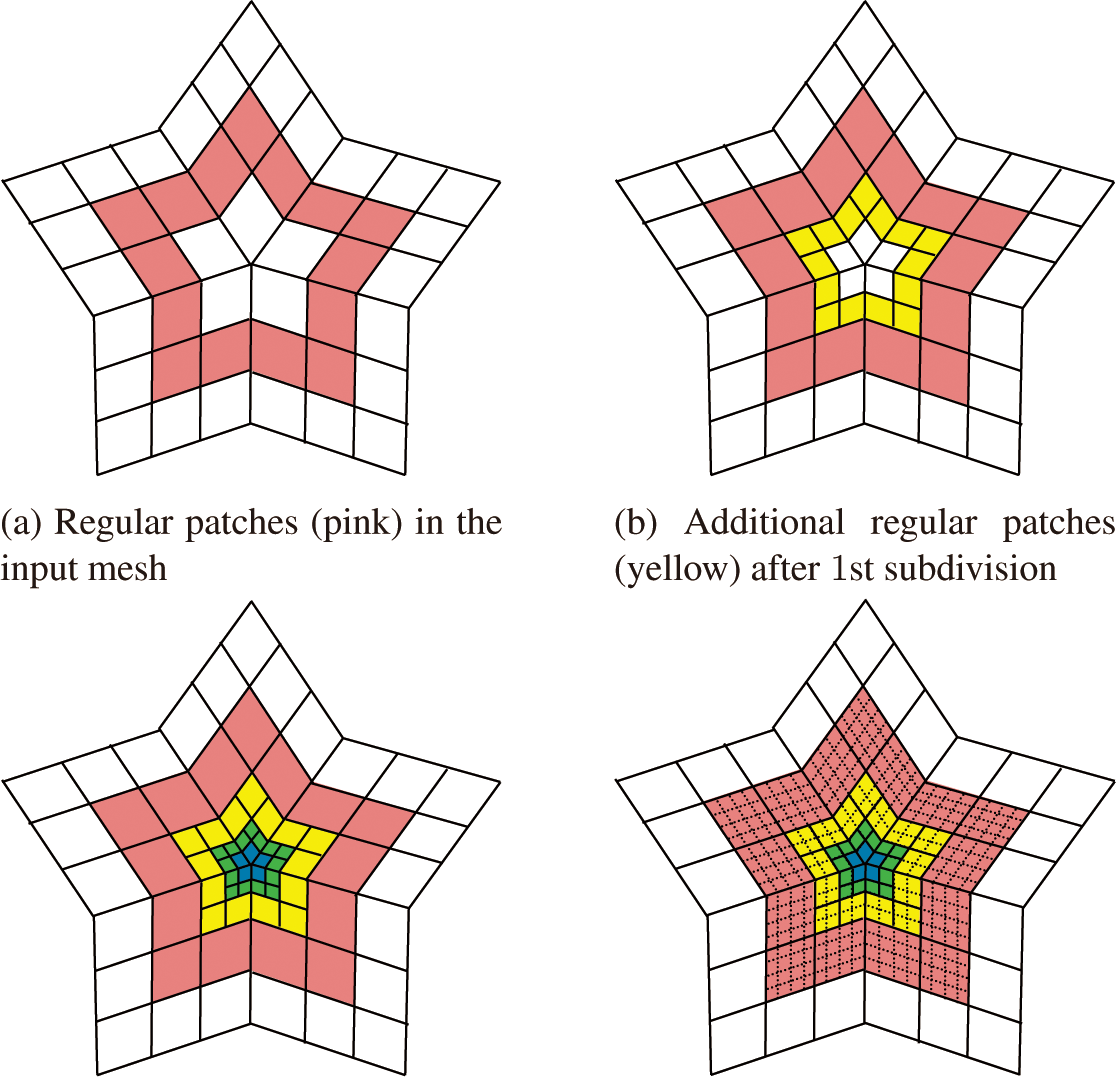
정규 패치들은 B-스플라인의 수식에 기반하여 좌표 및 노멀을 직접 계산한다. WebGPU에서 정점 쉐이더(vertex shader)에서 계 산하며, 기존에 전처리된 각 패치의 제어점 정보, 각 정점의 위치 정보를 스토리지 버퍼로 받아 (1)에 따라 계산한다. WebGPU 환 경에서는 테셀레이션 쉐이더를 지원하지 않기 때문에, 본 연구에 서는 전처리 단계에서 서브디비전 깊이에 맞춰 미리 분할된(pretessellated) 사각형 패치를 추출하였다. 각 서브디비전 깊이별로 추출된 패치는 렌더링 파이프라인(render pipeline)에서 적절한 해상도로 렌더링된다. 이 때 분할 해상도(tessellation resolution) 는 최대 서브디비전 깊이를 기준으로 계산한다. 본 프로젝트에서 는 최대 서브디비전 깊이를 6으로하였다. 가장 얕은 깊이에서는 패치 당 사각형 단위의 렌더링 해상도가 64 × 64이며, 가장 깊은 깊이에서는 단 하나의 사각형(1 × 1)으로 표현된다. (Figure 1,6) 이러한 구조를 통해 서로 다른 서브디비전 깊이의 패치들이 만나 더라도 정합성이 보장된다. 이와 같은 최적화된 구조는 WebGPU 환경에서 효율적인 데이터 관리와 빠른 연산을 가능하게 한다. B-스플라인 연산을 통한 곡면 정의 기법은 인스턴스 렌더링 방식 을 채택하여 WebGPU의 렌더 파이프라인에서 병렬적으로 렌더 링이 가능하다.
정규 패치와 비정규 패치가 맞닿는 경우, 해당 비정규 패치는 리밋 서피스에 수렴하지 못한 상태이므로 렌더링 시 크랙이 발생 할 수 있다. 따라서 비정규 패치를 이루는 정점들은 리밋 포지션 을 사전 계산하여 저장한다. 각 정점에 대해 자신과 연결된 인접 요소들로부터 연산에 필요한 정보를 추출하며, 해당 연산은 메시 구조의 정규성 여부와 무관하게 수행될 수 있도록 구성되었다. 이 연산은 데이터 간 의존성이 거의 없어 WebGPU의 컴퓨트 쉐이더 를 이용하여 병렬적으로 연산되도록 구현하였다. 비정규 정점을 제외한 비정규 패치의 정점들은 차수가 항상 4이므로, 이를 고려 해 아래과 같이 간결화한 수식을 사용하였다.
마찬가지로 리밋 노멀 역시 아래와 같은 수식을 사용하였다.
위에서 c2와 c3는 아래와 같다.
비정규 정점마다 계산된 리밋 포지션은 렌더링 단계에서 해당 정점의 위치를 결정하는 데 사용되며, 특히 곡면 경계에 위치한 비정규 정점들과 인접한 패치와 연속적으로 연결될 수 있도록 한 다. Figure 7에서 볼 수 있듯이, 전체 곡면에서 시각적인 일관성과 부드러운 연결성이 유지된다.

전처리에서 각 패치별로 16개의 제어점 좌표와 16개의 텍스처 좌표를 받는다. 이 구조는 하나의 정점이 여러 개의 텍스처 좌표 를 가질 수 있도록 하여 텍스처 심에서의 유연한 처리를 가능하 게 만든다. 또한, 전처리 단계에서 CC 서브디비전을 적용할 때 패치의 정점 위치뿐만 아니라 각 정점이 가진 텍스처 좌표까지 도 하나의 연산으로 함께 처리할 수 있어 CC 서브디비전을 통한 텍스처 매핑 시 유리한 구조를 제공한다. 인접한 패치 간 텍스처 값을 통일시키기는 작업은 WebGPU 버텍스 쉐이더에서세 가지 경우에 따라 구분하여 처리하였다.
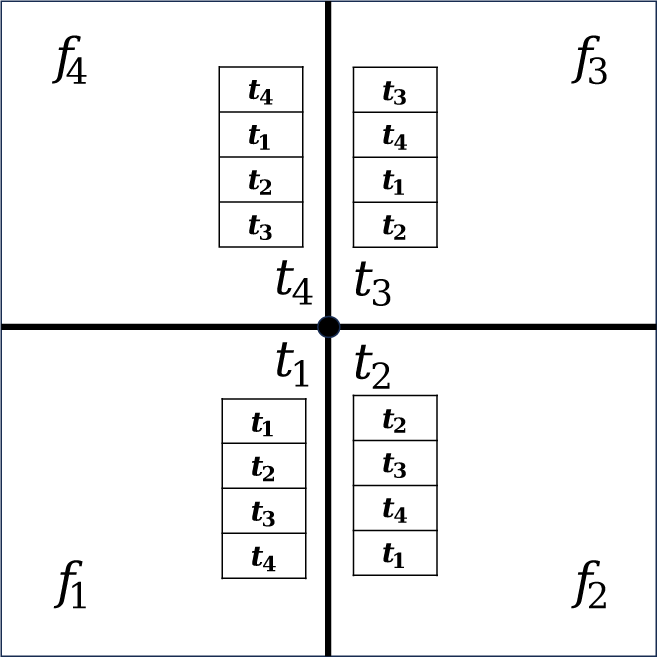
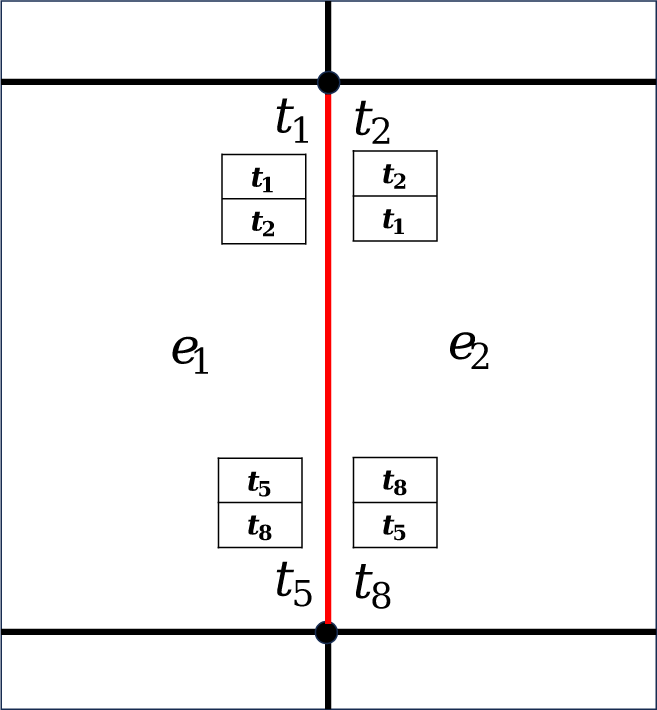
이처럼 텍스처 심에서 정점의 위치를 보정하여 연속된 곡면을 보장하였으며 Figure 10과 같이 크랙없이 디스플레이스먼트 매 핑이 적용됐음을 확인할 수 있다.
5. 실험결과
실험에서는 동일 모델에 제안하는 적응적 서브디비전과 모든 면을 서브디비전 하는 전면 서브디비전을 수행하고 각각의 경 우의 FPS, CPU 실행시간, GPU 실행 시간을 비교하였다. 실험 환경은 AMD Ryzen 5 5600H + NVIDIA GeForce 3050 Laptop GPU이며, 사용한 모델은 monster frog, ninja head, sphere 이다. (Figure 15) 실제 실험에서는 서브디비전 깊이를 6단계까지 설정 하여 진행하였으나, 전면 서브디비전의 경우 데이터의 양이 기 하급수적으로 늘어나 WebGPU 버퍼의 최대 크기를 초과해 렌더 링이 불가능한 경우가 생겨 각 모델을 렌더링 할 수 있는 최대 단계까지만 측정하였다.
FPS(Figure 11)의 경우 두 기법 모두 서브디비전 깊이(level) 가 커질수록 FPS가 줄어드는 경향을 보였으나, 전면 서브디비전 기법의 경우 적응적 서브디비전 기법에 비해 급속도로 줄어드는 것을 확인할 수 있었다.
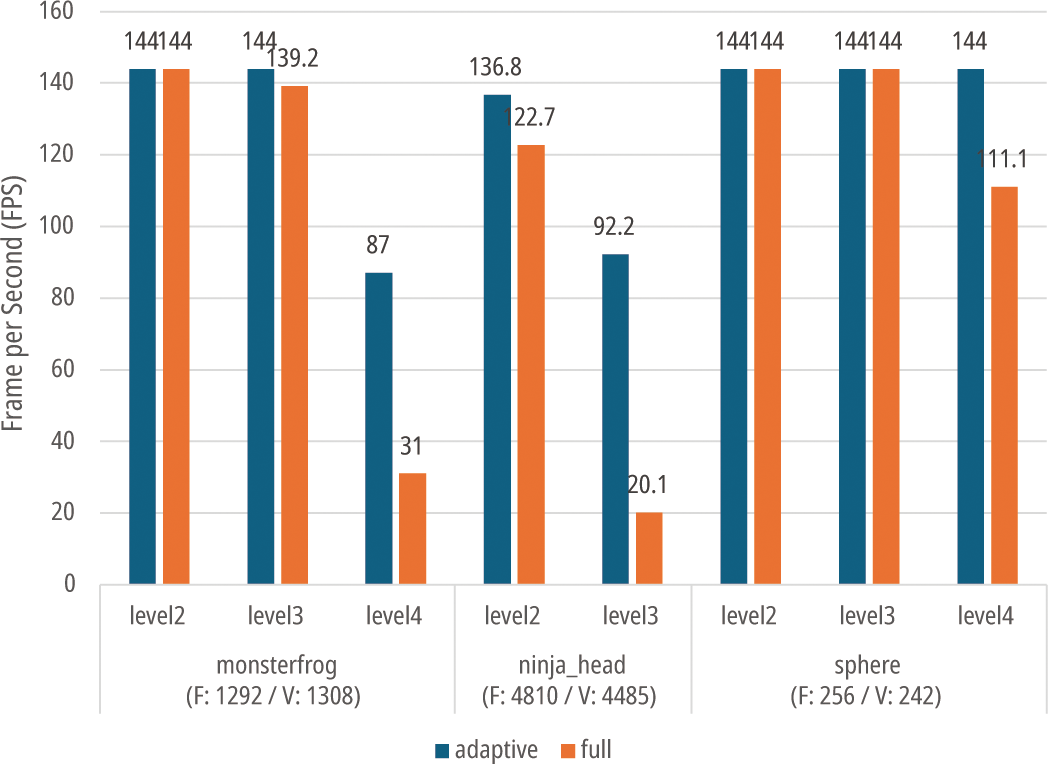
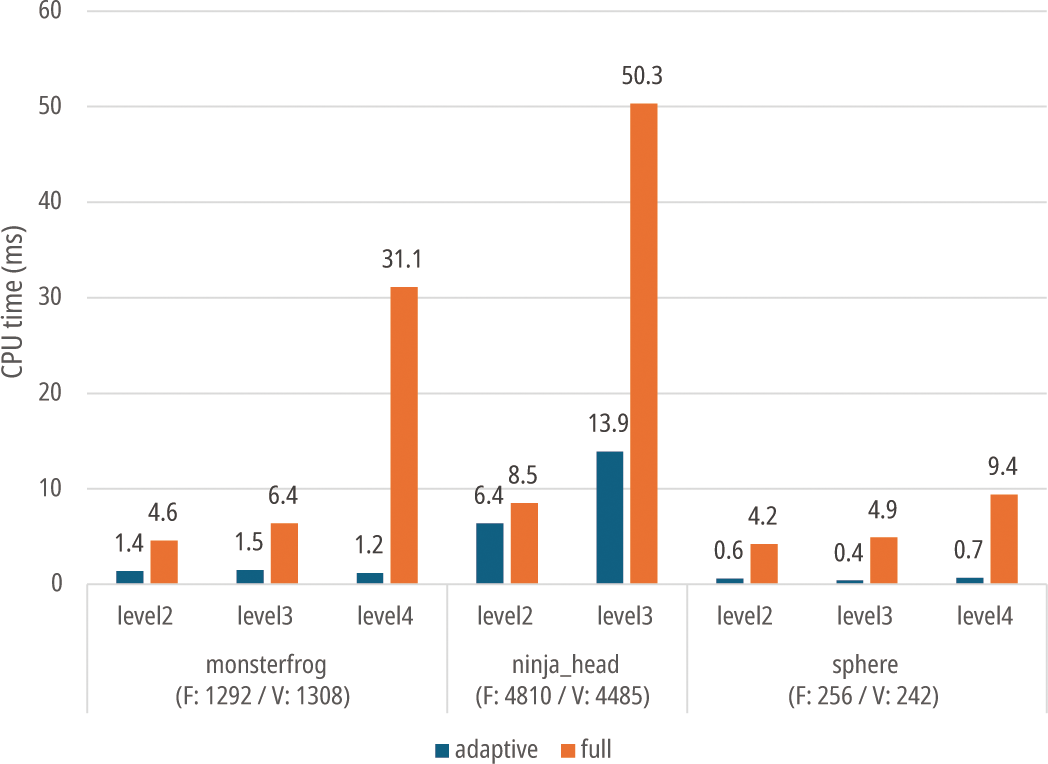
CPU 실행 시간(Figure 12)은 자바스크립트 실행 시간을 측정 하여 비교하였으며, 모델과 서브디비전 깊이에 따라 전면 서브디 비전을 시행한 경우가 적응적 서브디비전 시행시의 결과의 최소 약 3.3배에서 최고 25.9배까지 차이가 나는 것을 확인하였다.
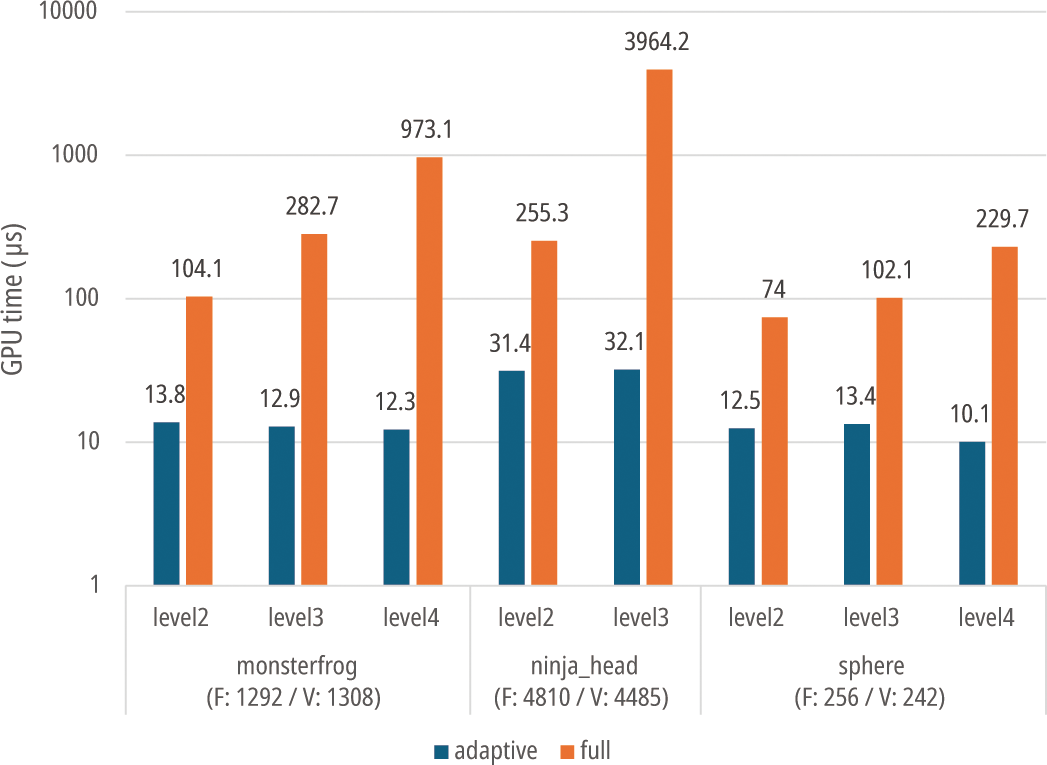
GPU 실행 시간(Figure 13)은 WebGPU의 인코더(encoder)가 생 성되는 순간부터 종료될 때까지의 시간을 측정하여 비교하였다. FPS와 마찬가지로 두 기법 모두 서브디비전 깊이가 커질수록 실 행 시간이 늘어났으나, 적응적 서브디비전 기법은 증가 추세가 완만한 반면 전면 서브디비전의 경우 실행시간이 기하급수적으 로 증가하는 것을 확인하였다.
또한 전처리 후 생성되는 데이터 파일의 크기도 의미 있는 차 이를 보였다. (Figure 14) 서브디비전 깊이가 증가할수록 전면 서 브디비전 기반 구조는 파일의 크기가 기하급수적으로 증가한 반 면, 적응적 서브디비전 기법은 서브디비전 깊이가 늘어나더라도 거의 파일의 크기가 대체로 동일하였다.
이러한 실험을 통해 고해상도 메시도 웹브라우저 환경에서 부 담없는 렌더링이 가능함을 확인하였고, 시각적 품질 또한 정성적 기준에서 검토되었다. 정규 영역에서는 B-스플라인 패치만으로 도 충분한 곡면 표현이 가능하였고, 비정규 영역은 리밋 포지션 기반 보간을 통해 주변 패치와의 연속성을 안정적으로 유지하였 다. 특히 텍스처 심에서 보정 로직의 효과로 인해 경계면에서의 위치 단절 없이 자연스러운 연결성이 확보되었다. 실제 렌더링 결과에서는 Figure 15와 같이 크랙이나 좌표 불일치가 시각적으 로 확인되지 않아 전체적으로 부드럽고 연속적인 곡면 표현이 가능했으며, 이는 데스크탑 환경과 유사한 품질을 제공함을 시사 한다.
6. 결론 및 향후 연구 과제
결과적으로, 본 연구에서 제안한 특징-적응형 구조는 기존 방 식 대비 성능, 메모리 사용, 시각적 품질 측면에서 모두 개선된 결과를 보였으며, WebGPU 기반 환경에서도 서브디비전 곡면을 실시간으로 고품질 렌더링할 수 있는 실용적인 대안으로 기능함 을 확인하였다. 현재의 방법은 B-스플라인 패치를 균등하게 사전 테셀레이션한 메시만을 사용하나, 향후에는 메시의 위상, 기하적 특징에 따라 테셀레이션의 해상도를 조절하는 적응적 사전 테셀 레이션이 적용된 메시를 사용하여 계산량을 줄이고 효율을 높이 는 방향으로의 연구가 필요하다. 또한 CC 서브디비전 기법 외에 다양한 서브디비전 기법을 실험하고 결과를 비교하는 후속 연구 를 계획 중에 있다. 이를 통해 제안한 방법의 일반성과 적용 가능 범위를 보다 체계적으로 검증할 수 있을 것으로 기대된다.