1 서론
가상 의료 시뮬레이션 소프트웨어는 임상의들이 실제 환자에게 시술을 수행하기에 앞서, 볼륨 데이터를 활용한 가상 환경에서 반복적 훈련을 가능하게 함으로써 시술 정확도를 높이고 의료 사고 위험을 줄이는 데 기여할 수 있다. 이때, 해부학적 구조의 정밀한 재현과 시술 과정 중 발생하는 물리적 반응의 표현은 중요한 요소이며, 이를 구현하기 위해서는 일정 수준 이상의 성능을 갖춘 물리 기반 시뮬레이션 엔진이 요구된다. 이러한 시뮬레이션은 단순한 시각화에 머무르지 않고, 절개나 봉합과 같은 외과적 조작이 인체 조직에 미치는 반응을 실시간으로 모사할 수 있어야 하며, 이를 위해 연산 속도, 물리적 정밀성, 시뮬레이션 안정성 간의 균형 확보가 중요하다 [1].
연부 조직의 물리적 거동을 표현하기 위해 다양한 물리 모델이 사용됐으며, 대표적으로 유한요소법(Finite Element Method, FEM) [2], 질량-스프링 모델 [3], 체인메일(Chain-mail) [4], 그리고 위치 기반 동역학(Position-Based Dynamics, PBD) [5] 등이 있다. 이 중 PBD는 비교적 간단한 연산 구조를 기반으로 하여 연산 속도 측면에서 우수한 성능을 보이며, 다양한 제약(Constraint) 조건을 통해 물리적 거동의 안정성을 효과적으로 제어할 수 있는 장점이 있다 [6]. 비록 FEM이나 기타 연속체 기반 모델과 비교하면 물리적 정밀도는 상대적으로 제한될 수 있으나, 실시간성을 요구하는 의료 시뮬레이션 분야에서는 정밀성과 실시간성 간의 균형 측면에서 유리한 선택이 될 수 있다. 특히 PBD는 병렬 연산에 적합한 구조를 갖추고 있어 GPU를 활용한 고속 시뮬레이션이 가능하며, 이는 고해상도 의료 데이터 기반 시뮬레이션의 확장성과 실시간성 확보에 기여한다 [7].
기존 PBD 기반의 연부 조직 시뮬레이션에서 주로 사용되는 거리 제약(Distance Constraint) [6]이나 부피 제약(Volume Constraint) [6]은 피부의 구조적 안정성을 유지하는 데에는 효과적이다. 그러나 이러한 제약 조건들은 외부 자극에 따라 피부가 보이는 확장 및 수축 반응이나, 장력이 방향성(Anisotropy)을 띠는 생체역학적 특성을 정밀하게 반영하지 못한다는 한계가 존재한다 [8].
이러한 문제를 해결하기 위해 본 연구에서는 PBD 체계에 새로운 물리 기반 제약 조건인 Skin Tension Constraint (STC)를 제안한다. STC는 피부 표면의 삼각형 요소를 기반으로 하여, 면적 변화율과 표면 법선 벡터 정보를 활용해 각 정점(Vertex)의 위치를 보정하는 장력 벡터장을 구성한다. 이러한 접근은 피부에 가해지는 자극의 방향과 크기에 따른 반응을 더욱 유연하게 표현함으로써, 기존 제약 조건의 한계를 보완하고 시뮬레이션의 정밀도와 안정성을 함께 확보하는 데 기여한다.
기존의 병렬 그룹핑 방식은 제약 조건 간 공유 정점을 기준으로 독립적인 엣지(Edge) 그룹을 구성함으로써 병렬 실행 가능성을 확보하는 데 중점을 두었다 [9]. STC는 각 제약이 삼각형 단위의 정점 정보를 포함하는 객체로 정의되며, 초기화 과정에서 각 객체는 고정된 정점 수(3개)와 초기 면적, 강성 계수 등의 파라미터를 바탕으로 구성된다. 이러한 구조는 기존 체계와의 충돌을 최소화하면서, GPU 커널에서 병렬 실행 준비를 단순화하는 데도 유리한 구조를 가진다. 특히 고해상도 시뮬레이션 환경에서의 확장성과 대화적 처리 가능성을 고려한 병렬화 유연성을 확보하는 데 중점을 두었다.
본 연구의 주요 기여는 다음과 같다.
-
1) 피부 장력 반응 특성을 정량적으로 모델링하고, 이를 기반으로 새로운 제약 조건인 STC를 정의하여 PBD 체계 내에 통합할 수 있는 구조로 설계하였다. 이를 통해 연부 조직의 물리적 반응을 더욱 세밀하게 모사할 가능성을 검토하였다.
-
2) CT 기반의 볼륨 데이터로부터 외부 피부 표면을 자동 추출하는 방식을 도입하여, STC 적용 대상을 물리 반응이 집중되는 경계 영역으로 제한함으로써 계산 효율성을 향상할 수 있는 여지를 마련하였다.
-
3) STC는 삼각형 단위로 정의되는 제약 조건 구조를 바탕으로 하며, 기존 병렬 그룹핑 방식과의 호환성을 유지하면서도 GPU 환경에서의 커널 초기화 효율을 높일 수 있는 구조적 특징을 지닌다.
-
4) 제안된 STC의 적용 가능성과 계산 효율성은 정적 절개 시나리오를 중심으로 한 초기 실험을 통해 검토되었으며, 피부 조직의 생체역학적 반응을 더욱 현실적으로 표현할 가능성을 탐색하였다.
2. 관련 연구
변형체 시뮬레이션(Deformable Body Simulation)은 컴퓨터 그래픽스, 물리 기반 애니메이션, 생체조직 모델링 등 다양한 응용 분야에서 핵심적인 기술로 자리 잡아 왔다 [10]. 특히 의료 영상 처리와 시뮬레이션 환경에서는 장기, 연부 조직, 피부 등 복잡한 재질의 거동을 사실적으로 구현하기 위해 해당 기법이 적극적으로 도입되고 있다 [11].
전통적인 변형체 시뮬레이션에서는 FEM이 높은 물리적 정확성을 제공하지만, 복잡한 선형 시스템 해결과 조건 수(Condition Number) 문제로 인해 실시간 응용에서는 계산 비용이 과도하다는 한계가 있었다 [4]. 질량-스프링 모델은 구현이 간단하지만 스프링 상수 설정에 따른 인공적 강성 문제와 수치적 불안정성으로 인해 현실적인 재료 특성 구현에 어려움이 있었다 [12]. 체인메일 모델은 국소적 변형 처리에는 효과적이나 전역적 물리 법칙의 일관성 유지와 복잡한 재료 특성 표현에 제한이 있었다 [13].
이를 해결하기 위한 대안으로 제안된 PBD는 Müller et al. (2007)에 의해 처음 도입된 이래, 간결한 수치적 구조와 높은 계산 안정성, 실시간 처리에 적합한 특성으로 인해 대화형 시뮬레이션 분야에서 폭넓게 활용되고 있다. PBD는 전통적인 물리력 계산 방식 대신, 제약 조건을 만족하는 방향으로 입자의 위치를 반복적으로 보정하는 알고리즘 구조를 채택함으로써, 계산의 안정성과 시스템의 응답성을 동시에 확보한다. 이러한 접근 방식은 특히 외력이나 사용자 상호작용에 신속히 반응해야 하는 실시간 시뮬레이션 환경에 적합하며, 병렬 연산 구조와의 높은 적합성을 통해 효율적인 구현이 가능하다는 장점이 있다 [7].
PBD에서 가장 널리 사용되는 제약은 거리 제약이다. 이는 두 정점 간 거리가 초기 상태의 기준 거리로 유지되도록 위치를 조정하는 제약으로, 물체의 구조적 안정성과 연속성을 유지하는 데 필수적인 역할을 한다. 거리 제약은 연속된 엣지를 따라 구성된 물체에서의 탄성 반응을 단순화된 계산으로 구현할 수 있도록 하며, 경량 계산 구조 덕분에 실시간 시뮬레이션에 적합하다 [6].
부피 제약은 일반적으로 사면체(Tetrahedron) 기반의 메시 구조에서 활용된다. 이 제약은 변형체의 체적 보존을 목표로 하며, 외부 압력이나 내부 자극에 대한 반응에서 실제 생체조직과 유사한 거동을 재현하는 데 필수적이다. 사면체의 부피는 벡터 연산을 통해 계산되며, 초기 상태 대비 부피의 차이를 줄이는 방향으로 정점 위치가 조정된다. 이는 특히 연조직, 장기, 유체 포함 조직 등 체적 유지가 중요한 시뮬레이션에서 필수적으로 요구된다 [6].
그 외에도 비틀림 제약(Bending Constraint)은 연속된 삼각형 또는 평면 간의 각도 차이를 제한함으로써 얇은 막이나 천의 굽힘 특성을 제어하는 데 효과적이다 [14]. 이러한 제약들은 2차원 및 3차원 변형체에서의 다양한 물리적 반응을 더욱 사실적으로 재현하는 데 중요한 임무를 수행한다.
다양한 제약 조건들에 관한 연구는 변형체 시뮬레이션의 정밀도와 안정성을 결정짓는 핵심 요소로서, 각각의 특성과 수학적 정의, 계산 비용에 따라 다양한 시뮬레이션 목적에 맞게 선택적으로 적용된다.
변형체의 가시화는 물리 기반 시뮬레이션의 계산 결과를 시각적으로 해석할 수 있는 형식으로 변환하는 과정을 포함하며, 이는 모델의 변형 상태를 정성적 및 정량적으로 분석하는 데 필수적이다. 특히 실시간 시뮬레이션에서 가시화는 시스템의 반응성과 직결되므로 고속 처리와 고해상도 출력을 동시에 만족시켜야 한다 [15].
이와 관련하여 본 연구에서는 변형 메시의 구조적 변화를 효율적으로 추적하고 시각화하기 위한 병렬 리샘플링(Parallel Resampling) 기법을 사용한다. 해당 접근은 변형체의 표면 또는 내부에서의 데이터 재구성을 위한 고속 기법으로, 일반적으로 GPU 기반의 병렬 연산 환경에서 수행된다. 리샘플링 과정은 원래의 메시 구조에서 유도된 정점들의 위치 변화에 따라 보간(Interpolation) 또는 재계산을 수행함으로써, 시각적 불연속이나 왜곡을 최소화하고, 시간에 따른 변화를 정확히 표현할 수 있도록 한다 [16].
또한 이러한 병렬 처리 기반 리샘플링은 시뮬레이션의 시간 프레임 간 결과를 연속적으로 연결함으로써, 동적 거동의 흐름을 부드럽게 시각화할 수 있는 장점을 제공한다. 특히 GPU를 활용한 대규모 정점 데이터의 처리와 병렬 커널을 이용한 볼륨 및 표면 데이터의 동시 연산은 실시간성과 정확성 모두를 만족시키는 데 핵심적이다. 이는 주로 의료영상 분야에서의 변형체 시각화에 활용되고 있다 [15].
3. 본론
본 연구에서는 인체 피부의 물리적 특성을 시뮬레이션하기 위해 새로운 제약 조건인 STC를 제안한다. 이는 피부 표면에 발생하는 인장력을 공간적으로 정량화하고 방향성을 갖는 벡터장으로 모델링함으로써, 생체 기계적 반응을 고해상도로 표현할 수 있도록 한다.
STC 적용을 위해서는 먼저 피부에 작용하는 인장력의 물리적 개념을 정의하고 [17, 18], 이를 기반으로 제약 조건을 설계해야 한다. 이를 위해 볼륨 기반 인체 데이터에서 정점-밀도 대응 과정을 수행하고, 경계 추출 알고리즘을 통해 피부 표면만을 선별한다. 해당 표면에 대해서만 STC를 적용함으로써, 실제 인체의 물리적 반응을 반영할 수 있는 선택적 제약 시스템을 구현하였다.
특히 피부의 장력은 해부학적 결(Langer’s lines)에 따라 일정한 방향성을 갖는 것으로 알려져 있으며 [19], 이를 반영하기 위해 각 삼각형 면(Face)을 단위 요소로 활용하였다. 정점 단위의 표현은 자극의 방향성과 강도를 동시에 나타내기에 한계가 있지만, 면 단위 요소는 국소적인 장력 방향을 표현할 수 있어 구조적 정합성과 계산 효율성을 높이는 데 유리하다 [20].
STC는 하나의 제약으로서 PBD의 기존 체계를 훼손하지 않고, 초기화 과정을 거쳐 Solve Iteration에서 투영(Projection) 과정을 통해 해결되며, 값이 정점에 반영된다 [6].
STC는 피부 표면의 인장 반응을 수치상으로 모델링하기 위한 제약 조건으로, 구조적 방향성과 물리 기반 복원력을 동시에 고려한다. 본 절에서는 STC의 수학적 구조와 물리적 기반 원리를 순차적으로 설명한다.
STC는 삼각형 면 단위로 정의되며, 각 면은 세 정점 P1, P2, P3 로 구성된다. 면적은 두 변 벡터 ab = P2 - P1, ac = P3 - P1의 외적을 통해 다음과 같이 계산된다:
이 외적 결과는 동시에 면의 법선 벡터를 제공하여 장력의 방향성을 정의하는 기준으로 사용된다 [21].
계산된 현재 면적 A와 초기 기준 면적 Arest 간의 차이 C = A - Arest는 제약 위반량(Constraint Violation)으로 정의되며, 복원력이 적용되어야 할 정도를 정량화하는 기준이 된다 [22].
각 정점에 적용되는 위치 보정 벡터는 면적 함수의 위치에 대한 그래디언트 ∇iC를 기반으로 산정되며, 이는 두 가지 주요한 물리적 특성을 갖는다. 첫째, 보정 벡터의 방향은 면적 그래디언트의 방향과 일치한다. 둘째, 보정의 크기는 면적 변화에 대한 민감도에 비례하여 결정된다. 이러한 보정 구조는 실제 물리 시스템의 반응을 수치상으로 근사하면서, 안정적인 힘 전달 및 계산 수렴성 확보에 기여한다 [23].
보정 벡터는 각 정점에 가해지기 전에 해당 정점의 질량에 반비례하는 가중치를 곱하여 분배된다. 이는 PBD의 핵심 개념 중 하나로, 질량이 큰 정점은 더 작은 반응을, 반대로 질량이 작은 정점은 더 큰 반응을 유도하여, 시뮬레이션 내 운동 특성을 정점별로 차등 적용할 수 있도록 한다. 이와 같은 방식은 고정된 정점과 자유롭게 움직이는 정점 간의 구속도를 반영하며, 외부 자극에 대한 물리적 반응의 현실성을 유지하는 동시에 전체 시뮬레이션의 수치적 안정성을 향상한다 [6].
피부는 늘어날 때 내부 콜라겐 섬유들이 순차적으로 당겨지며, 변화량에 따라 점차 강한 저항을 보이는 생물학적 특성을 보인다 [24]. 이러한 성질을 수치상으로 반영하기 위해, 본 연구에서는 삼각형 요소의 면적 변화에 따라 작용하는 복원력을 정의하였다.
복원력은 삼각형 요소의 면적이 기준 면적 Arest에서 벗어날 경우, 이를 원래 상태로 되돌리려는 방향으로 작용하는 가상의 탄성력이다. 특히, 인장 상태에서 복원력이 점진적으로 강화되는 피부의 특성을 반영하기 위해 비선형 증폭 함수를 도입하였다.
아래의 수식은 복원력에 적용되는 강화 계수 Famp를 정의한 것으로, 면적이 기준 면적을 초과할 때만 계수가 증가하도록 구성되었다:
이 정의를 통해 수축 상태에서는 초기 면적 기준의 일정한 복원 계수 k0에 따라 선형 탄성 복원력만을 적용하고, 인장 상태에서만 점진적으로 강화된 복원력을 유도할 수 있도록 설계하였다. 이러한 구성은 피부의 인장 방향 비선형성 [24, 18]을 수치상으로 반영하면서도 계산 안정성을 함께 고려한 형태이다.
앞서 정의한 STC는 피부의 방향성을 갖는 인장 반응을 표현하기 위해 설계된 물리 기반 제약 조건이다. 본 절에서는 STC가 PBD 체계 내에서 어떤 방식으로 구현되는지를 설명하고, 실제 시뮬레이션에서의 연산 흐름을 구체적으로 정리한다.
STC Solver는 각 삼각형 면을 하나의 독립적인 제약 단위로 간주하며, 각 면에 대해 현재 면적 계산, 제약 위반량 산출, 복원력 증폭, 위치 보정 계수 계산, 그리고 최종 위치 보정 벡터 도출의 절차를 차례대로 수행한다. 이러한 연산 과정은 아래에 제시된 알고리즘 구조에 따라 실행된다.
<Table 1>은 STC에 정의된 수식을 바탕으로 실행할 수 있는 알고리즘을 나타낸다. 이는 물리 기반 복원력 계산을 통해 PBD 기반 위치 보정이 어떻게 일어나는지 설명한다. <Table 1>에 제시된 구조는 기존 PBD의 거리 제약, 부피 제약 등과 같은 기본 투영 방식과 호환된다. 따라서 제안된 STC는 기존 PBD에 추가로 적용하여 실행되는 독립 제약 모듈이다.
4. STC 기반 피부 표면 탐지 및 병렬 연산 구조의 GPU 구현
본 장에서는 제안한 STC 기반 시뮬레이션 구조의 중요 구성 요소인 피부 표면 탐지 알고리즘과 병렬 연산 구조를 기술한다. STC는 삼각형 단위의 제약으로 정의되어, 면적 변화에 따른 비선형 인장 반응을 모사하며, 제약 간의 독립성이 높아 고해상도 시뮬레이션에서도 효율적인 병렬 처리가 가능하다. 이러한 구조는 기존 PBD 체계 내에서 특별한 재구성 없이 적용될 수 있도록 설계되었다.
STC의 적용 대상을 효율적으로 한정하기 위해, 본 연구에서는 물리 반응이 요구되는 외부 피부 표면만을 선택적으로 탐지하는 과정을 설계하였다. 이를 위해 Hounsfield Unit(HU) 기반 밀도 값을 갖는 볼륨 데이터로부터 생성된 정점 기반 메시를 기반으로, 각 사면체 내 정점들의 밀도 분포를 활용하여 공기와 접촉한 경계면을 자동으로 식별한다.
본 알고리즘은 사전에 정의된 HU 임곗값(minSkinDensity, maxSkinDensity)을 기준으로 각 정점의 상태를 분류하며, 밀도가 공기보다 높은 정점은 피부(Skin), 낮은 정점은 공기(Air)로 간주한다. 이후 각 사면체에 대해, 공기 정점이 하나만 포함된 경우에 한 해 나머지 세 정점을 피부로 판단하고, 이들로 구성된 삼각형 면을 외부 피부 표면으로 등록한다.
이러한 조건은 실제 피부 표면이 외부 공기와 접촉하고 있을 가능성이 큰 위치를 자동으로 추출하도록 하며, 불필요한 내부 구조에 대한 STC 적용을 배제할 수 있도록 한다. 다음 <Table 2>는 해당 피부 탐지 과정을 요약한 것이다.
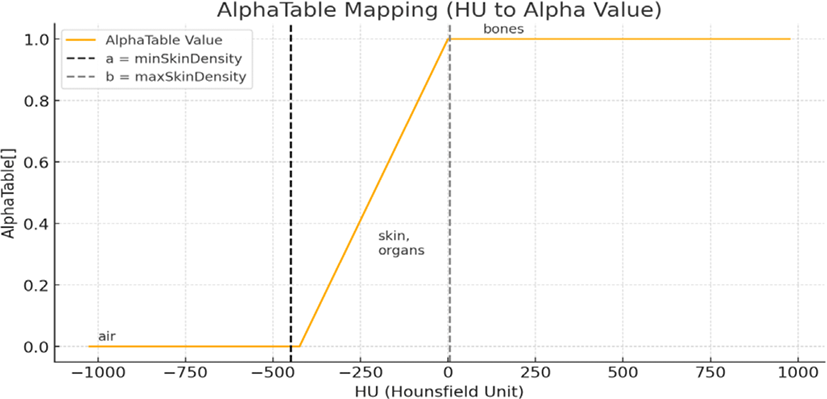
피부 표면을 정의하기 위해, 각 정점의 물리적 특성 중 밀도(Density)를 활용하여 공기 또는 피부로 분류하였다. 본 연구에서는 CT 기반 해부학적 볼륨 데이터의 HU 단위값을 기반으로, 공기에 해당하는 저밀도 구간과 연부 조직을 포함한 피부에 해당하는 고밀도 구간을 명시적으로 구분하였다.
이를 위해 사전에 설정된 밀도 임곗값을 이용하여, 각 정점의 밀도를 AlphaTable에 대응한 후 다음 기준에 따라 상태를 판정한다.
해당 테이블은 감도 조절이 가능하도록 설계되어 있으며, 실험에서는 피부의 임계 범위를 -449에서 6 사이로 설정하였다. 이 분류는 사면체 내 정점 분포 분석에 사용되어, 외부 공기와의 경계를 판별하는 데 핵심적인 역할을 한다.
이 기준은 탐지 정확도를 높이기 위해 구성 요소 기반의 탐색보다 더 정량적이며, 자동화된 경계 판별이 가능하게 하여 이후 시뮬레이션의 STC 적용 범위를 안정적으로 제한할 수 있도록 한다.
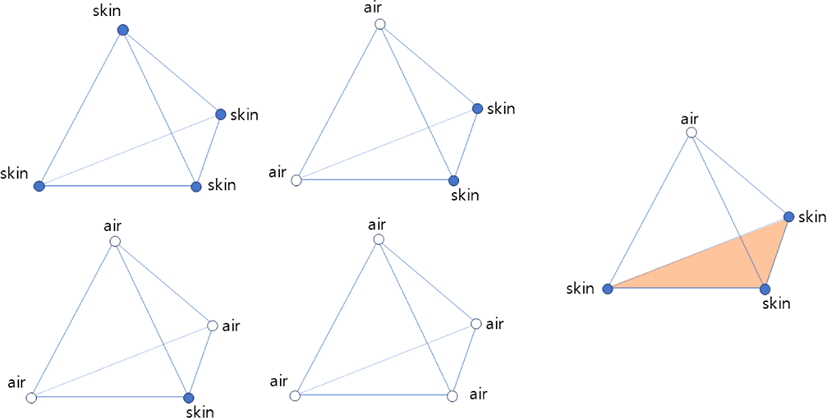
피부 표면으로 간주하는 면은, 각 사면체 내에서 공기와 접촉한 경계면으로 정의된다. 본 연구에서는 피부 표면이 외부 공기와 맞닿는 영역에서 발생한다는 점에 착안하여, 사면체의 네 정점 중 단 하나의 정점만이 공기로 분류되는 경우에만 면을 추출 대상으로 간주하였다.
해당 조건을 만족하는 경우, 공기 정점을 제외한 나머지 세 정점은 모두 피부로 판단되며, 이들 세 정점으로 구성된 삼각형을 피부 표면으로 등록한다. 이는 피부가 외부 공기와 접촉하면서 경계가 형성되는 상황에 해당하며, 내층 조직이나 체내 구조와는 구별된다.
이러한 탐지 방식은 다음과 같은 과정을 따른다.
-
사면체의 정점 4개 중 AlphaTable 값이 0인 공기 정점을 탐색
-
공기 정점이 정확히 1개인 경우, 나머지 3개 정점으로 삼각형을 구성
-
해당 삼각형은 표면으로 등록되어 STC의 대상으로 간주
이 조건은 공기 정점이 2개 이상이거나 전혀 없는 경우, 내부 조직 또는 경계 불명확 영역으로 간주하여 제외함으로써, 제약 조건이 적용되는 영역을 피부 표면으로 국한한다. 또한, 이는 연속적인 외피 구성면만을 선택적으로 활성화함으로써 시뮬레이션의 계산 효율성과 제약의 유효성을 동시에 확보할 수 있게 한다.
기존의 PBD 체계는 거리 제약과 부피 제약을 각각 엣지와 사면체 단위로 정의하며, 이는 주로 구조적 안정성이나 변형 방지에 초점을 맞춘 기하 기반 제약들이다. 그러나 본 연구에서 도입한 STC는 표면 삼각형 요소를 단위로 작동하며, 이는 복잡한 물리 기반 장력 반응을 구현하기 위한 세부적인 제약 구조를 요구한다.
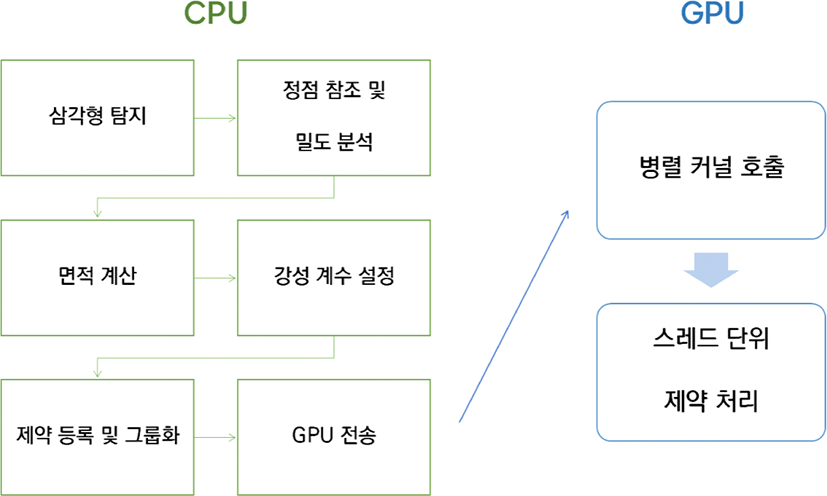
<Figure 3>과 같이 STC의 초기화는 전처리 과정에서 탐지된 표면 삼각형을 기반으로 이루어지며, 각 제약 항목은 다음의 세 가지 핵심 요소로 구성된다. 첫째, 제약을 구성하는 기본 단위로서 삼각형을 이루는 세 개의 정점에 대한 인덱스 정보가 포함된다. 이는 시뮬레이션 실행 시 해당 정점들의 좌표와 물리 정보를 참조하기 위한 필수 구조로 기능한다. 둘째, 초기 기준 면적(Rest Area)은 각 삼각형의 정점 좌표를 기반으로 한 3차원 공간상의 면적을 계산하여 설정된다. 이 값은 시간에 따른 면적 변화량을 기준으로 복원력을 산출하는 데 사용되며, 특정 위치(예: 절개 부위 근접 영역)에 따라 가중치를 조정하여 초기화할 수 있다. 셋째, 장력 강성 계수(Stiffness Coefficient)는 삼각형을 구성하는 정점들의 밀도 값을 평균한 후, 이를 기준으로 정규화하여 설정된다. 이 접근은 CT에서 추출된 HU 값이 조직의 물리적 밀도와 관련이 있다는 생리학적 특성에 착안한 것이다. 조직 밀도가 높을수록 일반적으로 더 강한 구조적 저항을 가지는 경향이 있으며, 이를 기반으로 STC에 적용되는 강성 계수를 개별 삼각형 단위로 차등화하였다. 이 계수는 생체조직의 물리적 반응 민감도를 수치상으로 조절하며, 각 제약 요소의 물리적 탄성 표현의 강도를 제어하는 주요 변수로 작용한다. 본 연구에서는 정규화된 밀도 기반 계수를 사용하였지만, 절개 위치나 시나리오에 따라 계수에 가중치를 부여하거나 위치 의존적 설정을 도입함으로써 유연한 제어도 가능하다.
초기화된 제약 구조는, 이후 병렬 연산 처리를 위해 정점 충돌이 발생하지 않도록 그룹화되며 GPU 메모리에 일괄 전송된다. 각 제약군은 병렬 커널로 개별 호출되어, CUDA 기반의 GPU 스레드들이 각자 하나의 제약을 할당받아 복원력 계산과 정점 위치 갱신을 수행한다.
<Figure 3>은 STC 초기화 및 실행 전 과정을 시각화한 흐름도이다. 좌측은 CPU에서 수행되는 탐지, 분석 및 초기화 단계를 보여주며, 중앙은 제약 등록 및 GPU 메모리로의 전송 과정을 나타낸다. 우측은 병렬 커널이 호출된 이후, 각 스레드가 독립적으로 제약을 처리하는 GPU 실행 구조를 표현한다. 이와 같은 구조는 병렬 연산 병목을 줄이고, 고해상도 메시 환경에서도 실시간 시뮬레이션이 가능한 성능을 제공한다.
본 연구에서는 STC의 병렬 처리 효율성을 확보하기 위해, 각 제약 조건이 독립적인 삼각형 단위로 구성된 구조적 특성을 활용하였다. 이러한 설계는 정점 간 충돌을 최소화하면서도 기존 PBD 체계의 병렬 그룹화 체계를 그대로 적용할 수 있도록 하며, 고해상도 시뮬레이션 환경에서도 안정적인 커널 실행을 가능하게 한다. 다음 절에서는 STC의 제약 구조가 병렬화에 어떻게 기여하는지, 그리고 GPU 커널 실행과의 연계 방식을 구체적으로 설명한다.
STC는 각 제약이 삼각형 단위로 정의되어 있으며, 정점 간의 연결성이 제한적이기 때문에 병렬 연산 구조에 적합한 형태를 가진다. 기존의 PBD 체계에서는 제약 조건 간 정점 충돌을 방지하기 위해 정점 공유 여부에 따라 제약을 여러 병렬 그룹으로 나누는 방식을 사용해 왔다. STC 역시 이러한 구조적 특성을 그대로 유지할 수 있도록 설계되었으며, 별도의 추가 그룹화 알고리즘 없이 기존의 거리 제약 처리 방식과 동일한 병렬 그룹핑 체계 내에서 처리할 수 있다.
STC는 각 삼각형 면이 독립적인 정점 집합을 기준으로 구성되기 때문에, 그룹화는 단순히 정점 간 공유 여부를 기반으로 수행된다. 각 제약은 사전에 정의된 정점 ID를 바탕으로 병렬 처리할 수 있는 그룹에 자동 할당되며, 충돌이 없는 경우에만 동일 그룹 내에 배치된다. 이러한 방식은 구조적으로 정점 충돌을 예방함으로써, GPU 환경에서의 커널 실행 안정성을 확보할 수 있도록 한다.
이와 같은 병렬 연산 구조는 복잡한 정렬 또는 추가적인 최적화 없이도 다양한 데이터에 적용할 수 있는 확장성을 보장하며, 실시간 시뮬레이션 환경에서 요구되는 처리 속도를 안정적으로 유지하는 데 기여한다.
5. 실험
본 연구는 CUDA와 C++을 이용하여 Visual Studio에서 직접 구현하였으며 실험은 NVIDIA GeForce RTX 3090을 장착한 개인용 컴퓨터에서 수행되었다.
실험에 사용된 인체 데이터셋은 익명화된 CT 데이터로 <Table 3>에 제시된 바와 같다. 정점 밀도 맵과 경계 추출 알고리즘을 활용하여 피부 표면만을 선별하였다. 이 과정에서는 외부 표면에 해당하는 정점군을 식별하고, 내층 구조는 제외함으로써 STC의 적용 대상을 실제 물리 반응이 필요한 영역으로 한정하였다.
| 데이터셋 | 해상도 | 특징 |
|---|---|---|
| Dataset A | 512 × 512 × 300 | 복부 |
| Dataset B | 512 × 512 × 544 | 머리 |
| Dataset C | 512 × 512 × 1152 | 다리 |
탐지된 표면은 STC가 적용될 삼각형 면들로 변환되며, 이후 시뮬레이션에서는 해당 영역만을 대상으로 제약이 작동한다. 또한, STC의 거동 차이를 명확히 비교하기 위해 피부 표면 일부를 정적으로 절개하는 방식을 도입하였다. 이를 통해 STC의 적용 여부에 따른 반응 차이를 정량적•정성적으로 평가할 수 있도록 하였다.
STC의 거동을 시각적으로 확인하기 위해, 본 연구에서는 실제 절개에 대응하는 정점 집합을 선택적으로 제약에서 제외하는 방식으로 간단한 정적 절개(Static Incision)를 구현하였다. 이는 복잡한 수술 시뮬레이션이나 상호작용 기반 모델이 아닌, STC의 적용 전후 차이를 비교•관찰하기 위한 시각적 장치로 설계되었다.
구현 방식은 다음과 같다. 먼저, 시뮬레이션 영역 내에서 절개 위치를 정의하기 위해 특정 위칫값을 기준으로 절개 경계를 설정하였다. 이후 피부 탐지 및 STC 적용 대상 탐색 과정에서 해당 경계 내에 속하는 정점들은 제약 초기화 단계에서 제외되며, 이에 따라 해당 영역의 피부는 물리적 제약 없이 자유롭게 거동할 수 있게 된다.
또한, 시각적인 절개 효과를 명확히 하기 위해 후처리 단계인 병렬 리샘플링 및 볼륨 가시화 단계에서는 해당 영역의 데이터가 제거된다. 사용자 혹은 관찰자는 절개 부위가 실제로 분리된 것처럼 인식할 수 있으며, STC가 적용되지 않은 영역의 물리적 반응을 명확히 비교할 수 있다.
이러한 절개 처리는 실제 상호작용 기반 수술 시뮬레이션에는 사용되지 않지만, 제약 기반 구조의 효과적 검증 수단으로 활용되었다. 특히, STC의 적용 여부에 따른 반응 차이를 직관적으로 평가할 수 있도록 설계되었으며, STC의 영향력을 구간별로 시각화하는 데에 중요한 역할을 한다.

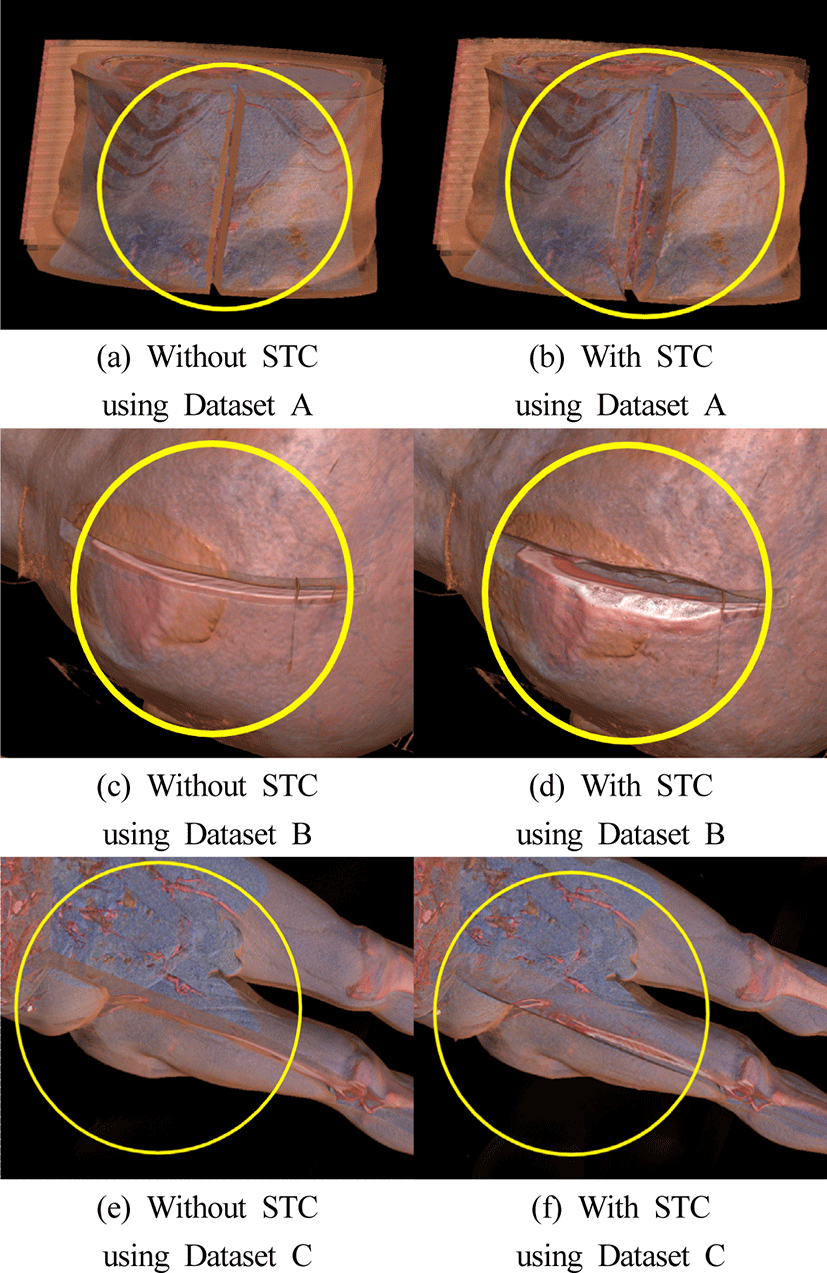
STC의 효과를 정성적으로 확인하기 위해, 동일한 절개 환경에서 STC 적용 여부에 따른 시뮬레이션 결과를 비교 분석하였다. 본 실험에서는 앞서 정의된 정적 절개 영역을 기준으로, STC가 적용되지 않은 경우와 적용된 경우의 피부 거동 차이를 관찰하였다.
<Figure 5>의 시뮬레이션 결과에 따르면, STC가 적용되지 않은 경우 (a), (c), (e)에서는 입자 간 상호작용이나 물리적 거동이 전혀 정의되지 않기 때문에, 절개 부위는 단순히 절개선에 따라 나뉜 형태로 유지되며, 주변 조직과의 연결이 고정된 채로 절개가 벌어지지 않는 비자연적인 형상을 보였다. 반면, STC가 적용된 경우 (b), (d), (f)에서는 절개 부위가 더욱 명확히 분리되고, 주변 피부 표면이 점진적으로 확산하며 벌어지는 움직임이 나타났다. 이는 실제 피부의 거동을 일정 부분 유사하게 재현하였을 가능성을 시사하며, 절개 시뮬레이션의 움직임 유효성을 높이는 데 일정한 기여를 하는 것으로 보인다.
본 절에서는 제안한 STC가 시뮬레이션 성능 및 병렬 처리 구조와의 호환성에 미치는 영향을 정량적으로 분석하였다. 이를 위해 서로 다른 해상도를 가지는 세 가지 Dataset(A, B, C)을 기반으로, STC 적용 여부에 따른 초기화 단계의 그룹핑 시간 차이를 비교하였다. 아울러, 전체 PBD 시뮬레이션의 성능을 평가하기 위해, 각 데이터셋을 기반으로 실행된 시뮬레이션에서 연속된 10개 프레임의 처리 시간을 측정하고, 이를 평균하여 프레임당 처리 시간을 산출하여 <Table 4>에 제시하였다. 시뮬레이션은 한 프레임 내에서 각 5회의 제약 조건 계산(투영) 단계를 반복하며 이루어졌고, 각 투영 단계에서는 거리 제약, STC가 차례대로 처리되었다. 또한 각 세부 단계는 CUDA를 이용하여 병렬로 처리되었다.
실험 결과, STC가 추가된 경우에도 세 데이터 모두에서 전처리에 해당하는 그룹핑 시간과 수행시간에 해당하는 커널 단위 병렬 처리 성능은 기존 방법에 비해 큰 차이가 없음이 확인되었다. 이는 STC가 삼각형 단위의 독립적인 제약 구조로 구성되어 있어, 기존 PBD 체계의 병렬 그룹핑 방식과 충돌 없이 통합할 수 있는 구조적 특성에 기인하는 것으로 해석된다. 또한, 제안된 STC는 피부 표면에 해당하는 경계 영역에 한정하여 적용되므로, 전체 볼륨에 걸쳐 정의되는 거리 제약이나 부피 제약에 비해 연산 대상이 되는 요소 수 자체가 10% 이하로 현저히 적기 때문에 총 연산 시간은 큰 변화가 없다.
전체적인 PBD의 연산 시간은 데이터 크기에 따라 다르지만 대화적 속도를 보이는 수준이다. 다만 실시간성을 위해 서라면 시뮬레이션 해상도를 실험보다 1/2로 낮추면 속도는 8배 증가하므로 이를 고려해야 한다.
6. 결론
본 연구는 연부 조직의 복잡한 물리적 반응을 정밀하게 표현하기 위해, 새로운 면 기반 제약 조건 STC(Skin Tension Constraint)를 제안하고 이를 PBD(Position-Based Dynamics) 체계에 통합하는 시뮬레이션 구조를 설계하였다. STC는 특히 피부와 같은 경계 조직의 비선형 인장 반응을 수치상으로 모델링하는 데 초점을 두며, 대화적 GPU 환경에서의 효율적 실행을 고려해 구성되었다. 본 연구의 주요 기여는 다음과 같은 네 가지로 요약된다.
첫째, STC는 삼각형 면적 변화를 기반으로 장력 반응을 수치화하고, 이를 PBD 체계에 통합함으로써 기존 제약 조건의 한계를 보완할 가능성을 제시하였다. 둘째, HU 값을 이용한 피부 경계 자동 탐지 기법을 통해 STC의 적용 범위를 효과적으로 제한하여 계산 효율성을 높였다. 셋째, STC는 독립적인 삼각형 단위 구조로 정의되어, 기존 병렬 그룹핑 방식과의 호환성을 유지하면서 별도의 최적화 없이도 효율적인 병렬 처리를 지원하였다. 넷째, 절개 시나리오를 통한 초기 실험에서 STC는 조직 변형에 따른 장력 반응을 표현할 가능성을 보였으며, 실험적 검토가 이루어졌다.
한편, 본 연구는 다음과 같은 몇 가지 제한점을 지닌다. 우선, 본 연구는 정적 절개 상황을 가정한 시나리오를 중심으로 수행되었으나, 실제 의료 시뮬레이션 환경에서는 동적인 절개 및 복잡한 조직 반응이 수반되므로 이에 대한 확장이 필요하다. 또한, 실시간 연산 성능이 필요하다면 비교적 낮은 입자 해상도를 사용해야 하므로, 더욱 세밀한 표현을 위해서는 추가적인 가속화 기법이 요구된다. 아울러, 장력 강성 계수는 입자의 밀도 값에 비례하는 방식으로 제안되었으나, 이러한 단순화된 접근은 조직의 비선형 물성을 충분히 반영하지 못할 가능성이 있다. 마지막으로, 피부나 근육의 섬유 방향과 같은 해부학적 구조의 방향성을 인장력 계산에 통합하는 방안에 대한 검토가 요구된다.
결론적으로, 본 연구는 STC라는 새로운 제약 모델을 통해 PBD 기반 연부 조직 시뮬레이션의 표현력과 병렬 확장성 향상 가능성을 제시하였다. STC는 장력 반응을 수치상으로 모델링하고, GPU 기반 병렬 구조와의 높은 호환성을 바탕으로 대화적 시뮬레이션 환경에서의 적용 가능성을 탐색하였다.
향후에는 본 모델을 동적 절개나 다층 조직 반응을 포함하는 복합 시뮬레이션으로 확장하고, 절개 부위에 따른 시뮬레이션 결과의 다양성을 반영하기 위해 파라미터 조절 기법을 정교화할 필요가 있으며, 이와 함께 절개 움직임의 사실성에 대한 정량적 평가 체계의 도입도 필요하다. 또한, 더욱 높은 입자 해상도에서도 실시간성을 유지하기 위한 연산 최적화, 특히 GPU 기반 병렬 그룹핑 처리의 개선을 통해 고해상도 환경에서도 효율적인 처리가 가능할 것으로 기대된다. 이러한 발전을 통해, 실제 임상 시나리오에서의 상호작용 기반 의료 시뮬레이션 환경에 STC 기법을 안정적으로 적용함으로써 그 활용 범위를 더 넓혀갈 수 있을 것이다.