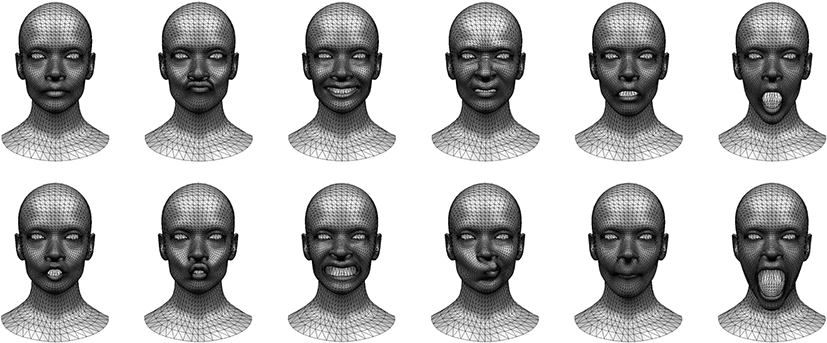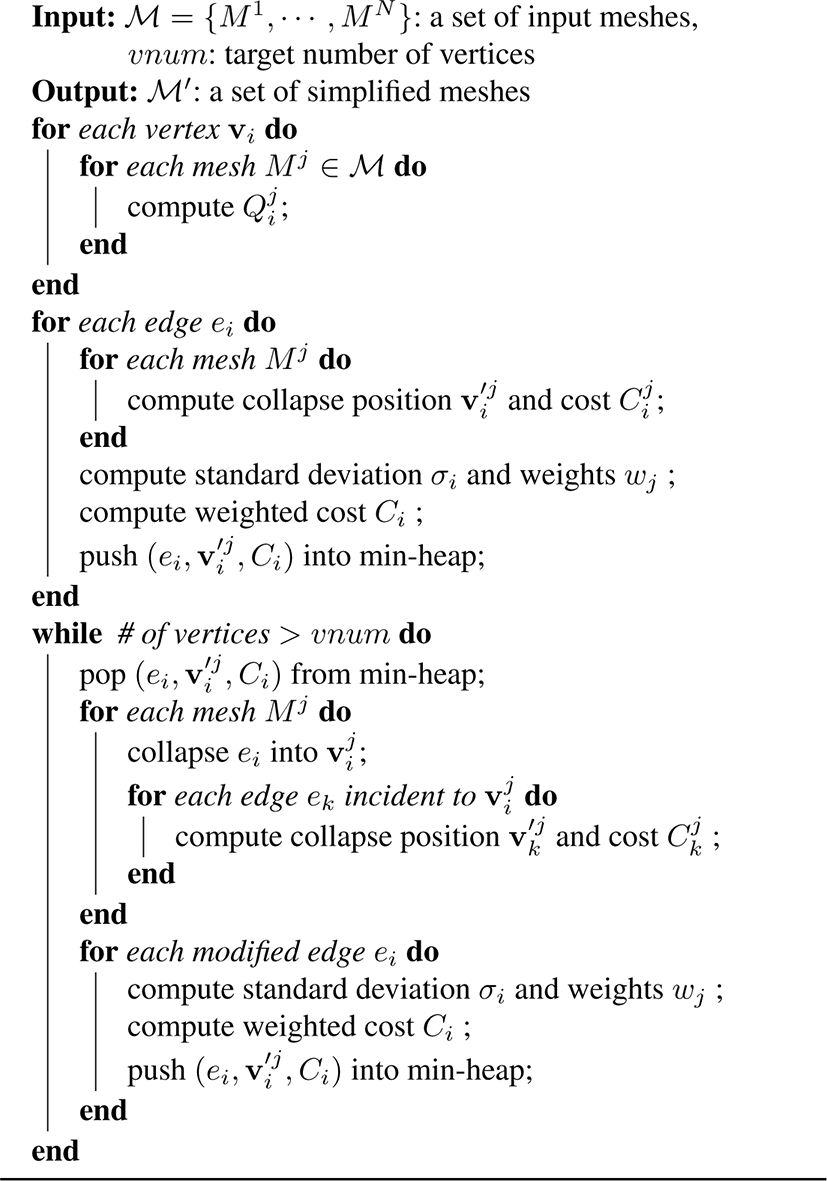1. 서론
컴퓨터그래픽스 기술의 비약적인 발전으로 영화 및 애니메이션제작에 가상의 3D 캐릭터의 등장은 새로운 일이 아니다. 국내 및해외의 영화 업계에서 작품을 살펴보면 과거와 비교할 수 없을정도의 많은 CG장면과 그 속에 등장하는 3D 캐릭터의 숫자는점점 증가하는 추세이다 [1]. 얼굴 표정은 영화나 애니메이션에서 캐릭터의 특징을 나타내기 위한 중요한 수단이기 때문에 더욱 사실적이고 풍부한 얼굴 애니메이션을 만들기 위한 기술이 실제산업에서 사용되어 왔다. 블렌드쉐입(blend shape) 기법은 고품질의 3D 얼굴 애니메이션을 생성하기 위해 가장 널리 사용되는방법이며, 특히 영화 업계에서 현실적인 휴머노이드 캐릭터를만들기 위해 주로 사용된다 [2]. 블렌드쉐입은 무표정의 베이스쉐입(base shape)의 형상을 변형시켜 다른 표정의 타겟쉐입(targetshpae)을 생성하고, 두 형상간의 선형보간을 통해 새로운 얼굴 표정을 합성하는 기술이다. Figure 1처럼 무표정 형상을 가진 베이 스쉐입이 있다고 하자. 정점의 개수와 연결구조가 동일한 복사본모델의입술 양끝 정점을 움직여서 웃는 형상을 가진 타겟쉐입을얻으면 두 개의 모델은 형상은 다르지만 정점의 개수와 연결 정보가 동일하기 때문에 모든 정점에 대해 일대일 대응관계를 생성할수 있다. 즉 두 모델은 정점의 개수, 각 정점의인덱스 뿐만 아니라정점들간의 연결 정보가 서로 동일하다. 따라서 무표정 모델의 정점을 시간에 따라 웃는 얼굴 모델의 정점 위치로 이동시켜 얼굴애니메이션을 생성할 수 있다.

얼굴 모델이 수백만개의 폴리곤으로 이루어져 있는 경우 고성능 그래픽스 하드웨어에서조차 이를 처리하기 위한 비용이 크다. 따라서 얼굴 애니메이션을 수행하기 전에 각각의 모델을 단순화할필요가 있다. 하지만 정점의 개수와 연결 정보가 모두 동일한얼굴 모델 집합에서 각각의 모델을 단순화했을 때 정점의 연결 정보가 서로 달라지는 문제가 발생한다. 결국 모델 정점간의일대일대응관계가 사라지기 때문에 더이상 단순화된 모델간에 블렌드쉐입 기법을 적용하기 어려워진다. 본 논문에서는 이러한 문제를해결하기 위해 다수의 삼각 메쉬에 대하여 정점의 개수와 연결정보를 유지하는 동시 단순화 기법을 제안한다.
본 논문의 구성은 다음과같다. 제 2절에서는 블렌드쉐입 및 메쉬 단순화와 관련된 이전 연구를 소개한다. 제 3절에서는 기존에널리 사용되는단일 메쉬의 단순화 기법을 설명하고, 제 4절에서는 확장된 에지 제거 정보를 이용하여 단일 메쉬의 단순화 기법을다수의 메쉬로 확장한다. 제 5절에서는다양한 실험을 통해 제안된 기법의 안정성과 유효성을 보이고, 끝으로 제 6절에서는 결론및 향후 연구방향을 제시한다.
2. 관련 연구
지금까지 다양한 얼굴 애니메이션 기술이 개발되어 왔다. 그 중전통적인 방식인 키프레임 사이에 선형 보간법을이용하여 중간 프레임을 생성하는 방식은 Parke와 Frederick [3]가 처음으로제안하였다. Lewis 등 [4]은 블렌드쉐입 기법을위상적으로 일치하는 여러 형상의 선형 가중치 합으로 설명하면서 슬라이더인터페이스를 이용하여 가중치를 조절하는 예를 보여주었다. 타겟쉐입의 모델수가 많거나 모델의 삼각형 수가 많은 경우 얼굴 애 니메이션을 가속화하기 위한 몇몇 연구도 진행되었다. Seo 등 [5]은 대용량의 블렌드쉐입 모델을 압축하여 하드웨어 가속 애니메이션을 수행하는 방법을 다루었으며, 행렬 블록 재정렬(roworder reordering)과 HSS (hierarchically semi-separable) 표현에 기반한행렬 압축 기법을 제시하였다. Costigan 등 [6]은 GPU에 블렌드쉐입 모델을 저장함으로써 속도가 향상되는 애니메이션 기법을제시하였다. 아직까지는 얼굴 애니메이션 처리를 가속화하기 위한 타겟쉐입을 동시적으로 단순화하는 연구는 진행되지 않은 상황이다.
본 논문에서 제시하는 알고리즘의 목표는다수의 폴리곤모델을동시에 단순화하며 위상을 같게 유지하는 것이다. 지금까지 많은 종류의 메쉬 단순화 알고리즘이 제안되었다. Schroeder 등 [7] 은 국소적 지오메트리를 검사하면서 정점을 점진적으로 제거하였다. [8]에서는 메쉬표면 위에 새로운 정점을 생성하고곡률이높은 영역에서 많은 정점을 분포시키며메쉬를 재구성(re-tiling)하는 방법을 제시하였다. 이 방식은 날카로운 모서리를 가진 메쉬보다는 비교적 매끄러운 표면으로 이루어진 메쉬에 적합하다. Kalvin과 Taylor [9]는 삼각형을 병합하는 방식으로 단순화를 수행했다. 이 방식은 얼굴 모델보다는 날카로운 모서리를 많이 가진 모델에 더 적합하다. Garland와 Heckbert [10]가 처음으로 2차에러 측정법을이용하여 폴리곤 모델을 단순화하는 알고리즘이제시하였다. [11]에서는 메쉬의 볼륨이 선형적으로 변화하며 단순화가 진행된다. Cignoni 등 [12]은이전 알고리즘의 성능을 분석 비교한 결과를 제시하였다. 메쉬 단순화 알고리즘의 정확도는메쉬의 기하학적 구조나 위상정보 등에 따라 크게 좌우된다. 이후Pauly 등 [13]은 곡률이 높은 영역에 더 많은 정점을유지시키기위해 국소 변이 추정과 2차 에러 측정법을 사용하였다. 그러나 이기법은 메쉬 단순화를 포인트 클라우드 기반에서 수행한다는 점에서 멀티레벨 스무딩, 다중 해상도 모델링과같은 포인트 기반프로세싱 어플리케이션에 더 적합하다. Kim 등 [14]은 곡률이 높고 형상이 얇은 영역에서는 2차 에러 측정법이 정확한 기하학적오차를 측정하는 것이 어렵다는 점을 보완하여 날카로운 형상의영역을 보존하기 위한 단순화 기법을 제안하였다. Ran 등 [15]이제시한 방법은 메쉬의 날카로운 특징을잘 보존한다는 장점이있지만 지역적 들로네(delaunay) 조건이유지되어야 한다는 점에서제한적이다. 본 논문에서는 많은 문헌에서소개된 2차 에러 측정법을이용한 메쉬 단순화를 간략히 소개하고, 다수의 삼각 메쉬에대해 확장하는 기법을 제안한다.
3. 단일 메쉬의 단순화
본 절에서는 Garland와 Heckbert [10]가 제안한 단일 삼각 메쉬에 대한 단순화 기법을 요약한다. 제 4절에서는 이를 다수의 삼각메쉬에 대한 동시 단순화 기법으로 확장한다.
3차원 공간의 한 점 v = [x y z 1]T 에서 임의의 평면 π: ax+by+cz + d = 0 까지 거리의 제곱(squared distance)은 다음과같이 2차식으로 표현될 수 있다:
여기서 p = [a b c d]T 는 단위법선(a2 + b2 + c2 = 1)을 갖는 평면π의 동차좌표(homogeneous coordinates) 표현이고, K는다음과같이 계산되는 대칭행렬이다:
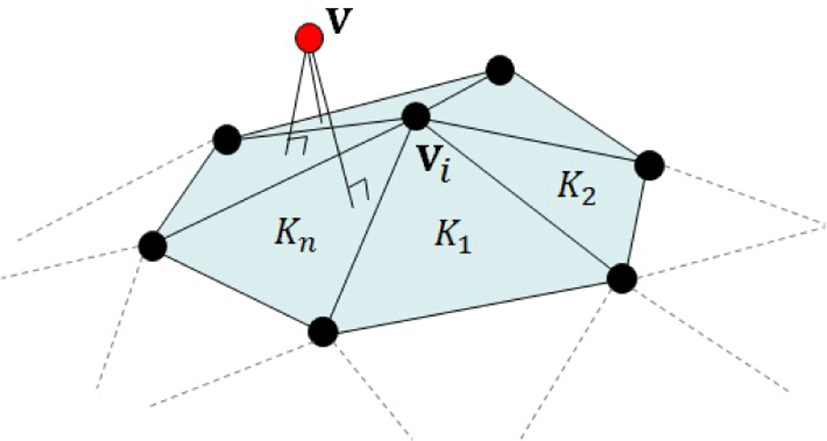
Figure 2에서 삼각 메쉬 위의 한 정점 vi을 공유한 n개의 삼 각형을 가정하자. 메쉬 외부의 한 점 v에서 삼각형을 포함한 각평면까지의 거리 제곱의 합은 다음과같이 계산될 수 있다:
여기서 Kj는 각 삼각형을 포함한 평면으로부터 식 (1)을 통해 계산되는 행렬이며, 는 정점 vi에서 정의되는 QEM (quadratic error metric) 행렬이라고 한다. 메쉬 단순화 기법에서행렬 Qi는 한 점 v에서 정점 vi주변의 메쉬까지의 형상의 차이(에러)를 측정하기 위해서 사용된다.
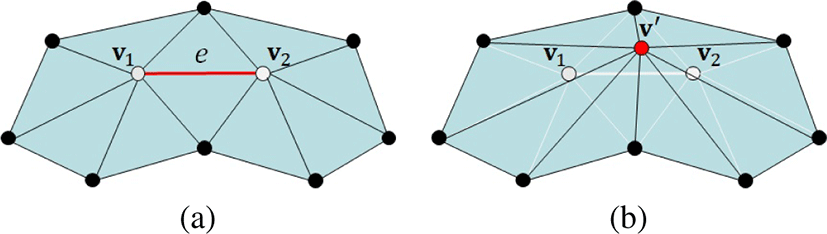
삼각 메쉬에서 반복적으로 에지를 제거(collapse)함으로써 단순화된 메쉬를 얻을 수 있다. Figure 3은 v1과 v2를 양 끝점으로 하는 에지 e = (v1, v2)를 제거하는 과정을 나타낸다. 에지 제거 과정은 (1) v1과 v2를 v′으로 병합하고, (2) v2와 연결된 에지를 v1에연결하고, (3) 사용되지 않는 삼각형을 제거하는단계로 구성된다.
에지 제거로 단순화된 메쉬(Figure 3(b))는 제거 전 메쉬(Figure 3(a))와 형상의 차이를 갖는다. 이러한 형상의 차이는 에지 제거에 따른 비용으로 정의될 수 있으며, 이는 v′에서 제거 전 메 쉬의 삼각형을 포함한 평면들까지의 거리 제곱의 합으로 다음과 같이 계산될 수 있다:
여기서 Q1과 Q2는 각각 정점 v1과 v2에서 계산된 QEM 행렬이다. 에지 제거 비용은 정점 v′의 위치에 따라 달라지므로 최소의제거 비용을 갖는 v′의 위치는 를만족하는해 (x̂, ŷ, ẑ)를 구하여 찾을 수 있다.
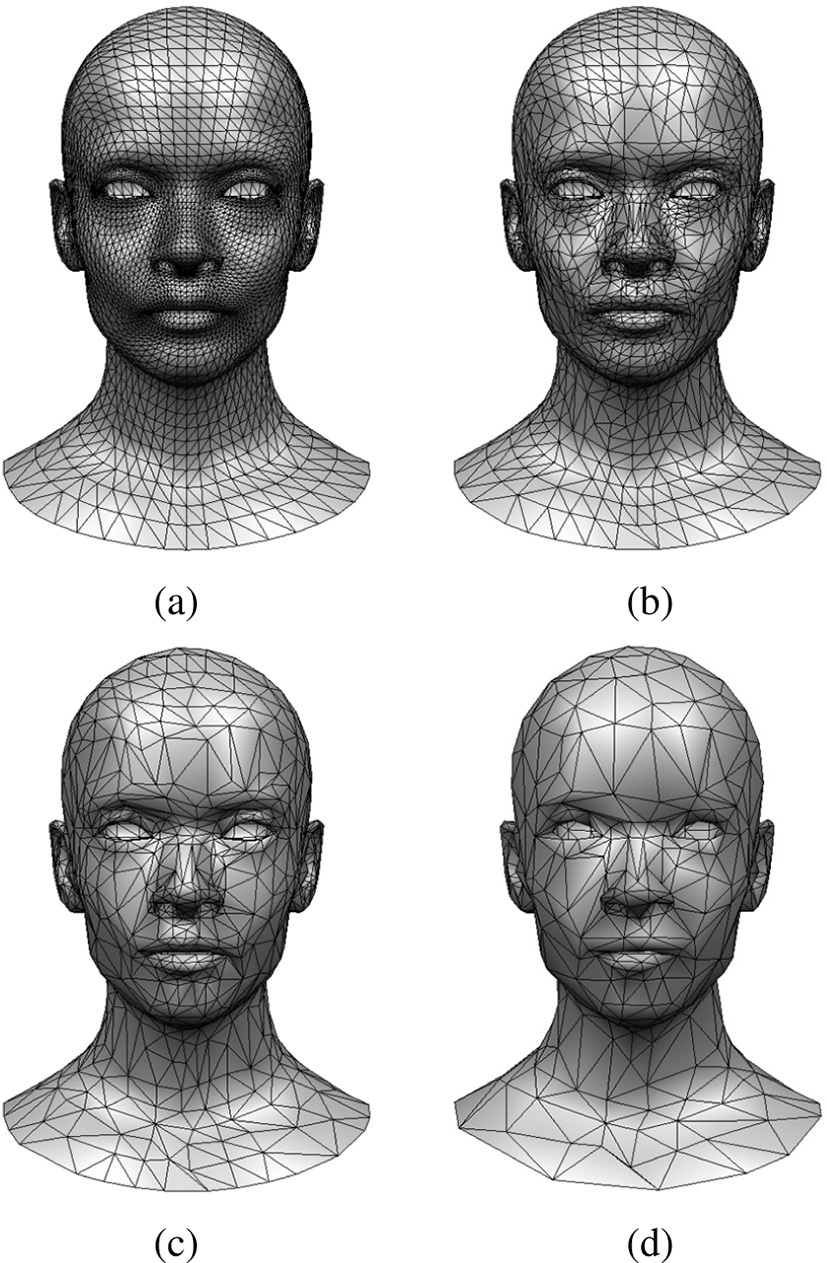
메쉬를 구성하는 각각의 에지 ei에 대하여 제거 위치와 비용으 로 구성된 에지 제거 정보 (ei, v′i, Ci)를 구하여 최소힙(min heap)에 저장한다. 최소힙은 에지 제거 비용이 가장 적은 에지를 루트에 유지하므로, 최소힙에서 순차적으로 에지 제거 정보를 꺼내어해당 에지를 제거하면 원본 삼각 메쉬와 형상의 차이를 최소로하는단순화 메쉬를 얻을 수 있게 된다. Algorithm 1은 단일 메쉬에 대한 단순화 알고리즘을 나타내고, Figure 4는 얼굴 메쉬에단순화 기법을 적용한 결과를 나타낸다.
4. 다수 메쉬의 동시 단순화
본 절에서는 앞에서설명한 단일 메쉬의 단순화 기법을 확장하여동일한 연결 정보를 갖는 N개의 삼각 메쉬에 동시에 적용하는 기법을 제안한다. 제안된 알고리즘은 N개의 메쉬를 동시에 단순화할 때, 에지 제거 순서를 동일하게 적용하여 최종적으로 얻어진단순화 메쉬들이 동일한 정점의 수와 연결 정보를 갖도록 한다.
일반적으로 블렌드쉐입 모델은 중립(neutral) 표정을 갖는 메쉬에서 변형된 다양한 표정을 갖는 메쉬들로 구성된다. 블렌드쉐입을구성하는 메쉬들은 하나의 메쉬에서 변형되었기 때문에 동일한정점의 수와 연결 정보를 공유한다. 다양한 표정들을 갖는 메쉬들을 가중치를 기반으로 선형결합을 하면 새로운 표정을 갖는메쉬를 생성 할 수 있다. 본 논문에서 제안하는 동시 단순화 기법은이러한 제약 조건 즉, 동일한 정점의 수와 연결 정보를 갖는다수의 메쉬들을 대상으로 한다. Figure 5은 본 논문에서 사용한블렌스쉐입 모델의일부 메쉬들을 나타내다.
제 3절에서 정의한 에지 제거 비용은 에지 주변의 메쉬 형상에따라 달라진다. 따라서 N개의 메쉬가 동일한 정점의 수와 연결정보를 갖더라도, 메쉬의 기하학적 형상이 다르면 각 에지의 제거비용은 메쉬에 따라 서로 다르게 된다. 결과적으로 기존의 메쉬단순화 기법을 브렌드쉐입을 구성하는 각각의 메쉬에 개별적으로 적용할 경우, 제거되는 에지의 순서가 메쉬마다다르기 때문에최종적으로 단순화된 메쉬들은 서로 다른 연결 정보를 갖게 된다. 이러한 결과 메쉬들에 대하여 블렌드쉐입 기법 즉, 가중치를 이용한 선형 결합을 적용할 경우원하지 않는 결과를 초래하게 된다. 본 논문에서는 이러한 문제를 해결하기 위해 N개의 메쉬의 형상을 동시에 고려하여 확장된 에지 제거 정보를 구성하고, 이를기반으로 모든 메쉬에서 동일한 순서로 에지를 제거하는 기법을제시한다.
동일한 정점의 수와 연결 정보를 갖는 N개의 메쉬 집합 = {M1, M2, …, MN}을 가정하자. 메쉬 Mj의 에지 ei의 제거 비용을 라고 하면, 모든 메쉬를 고려한 에지 ei의 제거 비용 Ci는다음과같이 계산될 수 있다:
여기서 wj는 메쉬 Mj에 대한 에지 ei의 제거 비용에 대한 가중 치이다. 모든 메쉬에 대하여 가중치가 wj = 1인 경우, 에지 ei의제거 비용은 단순히 모든 메쉬에서 해당 에지의 제거 비용을 합한결과와 같다. 본 논문에서는 에지 ei의 제거 비용의 가중치를 각 메쉬마다 다르게 적용한다. 적절한 가중치 wj를 설정하기 위해 각각의 메쉬 Mj에 대하여에지 ei의 제거 비용 를 계산한다. 만약 제거 비용 가 모든 메쉬 모델에 대하여 동일하거나 거의유사하다면, 이러한 결과는 에지 ei주변에서 각 메쉬의 형상이 크게 변형되지 않기 때문이다. 반면, 에지 ek는 메쉬 모델에 따라 제거 비용 의 변화가 크다고 하면, 이는 에지 ek주변에서 각메쉬의 형상의 변화가 크다는 것을유추할 수 있다. 제거 비용의변화가 큰 에지 ek는 ei에 비해 상대적으로 각 메쉬들에서 형상의 중요한 특징을 표현한다고 해석 할 수 있다. 따라서 이러한 에지들은 제거 비용을 더 크게하여 단순화 과정에서 제거되지 않도록한다.
각 메쉬에 대하여 에지 ei의 제거 비용의 표준 편차(standard deviation)를 σi라고 하자. σi가 작은 에지 ei는 각 메쉬에서 형상의 변화가 적은 부분에 포함되는 에지이므로 낮은 가중치를 할당하여에지 제거의 순위를 높일 수 있다. 반면, 제거 비용의 표준편차가 큰 에지는 높은 가중치를 할당하여 해당 에지가 제거되지않도록 할 수 있다. 이러한 원리를 적용하기 위해 본 논문에서는다음과같은 표준 편차에 따른 가중치 함수를 이용하였다:
여기서 σmax는 사용자가 정한 에지 제거 비용의 최대 편차를 나 타내고, 가중치는 0.1 ≤ w ≤ 1의 범위에 포함된다. 확장된 에지 제거 정보는 Figure 6와 같이 각 모델에 대한 에지 제거 비용과가중치 그리고 모든 메쉬를 고려한 제거 비용으로 구성된다. Algorithm 2은 확장된 에지 제거 비용을이용하여 다수의 메쉬에대한 동시 단순화 알고리즘을 나타낸다.
5. 실험 결과
본논문에서 제안한 다수의 메쉬에 대한 동시 단순화 기법은 C++ 언어를 사용하여 Intel i7-7700K 4.2 GHz CPU, 8GB의 메인 메모 리와 NVIDIA GeForce GTX 1060 그래픽 카드가 설치된 PC에서 구현되었다. 삼각 메쉬를 표현하기 위해 Kettner [16]가 제안한 하프에지(half edge) 자료구조를 활용하였다. 삼각 메쉬에 대한 하프에지 자료구조는 메쉬의 기하학적 연결 정보를 실시간으로 빠르게 얻을 수 있기 때문에 제안된 기법의 계산 성능 향상에 기 여할 수 있다.
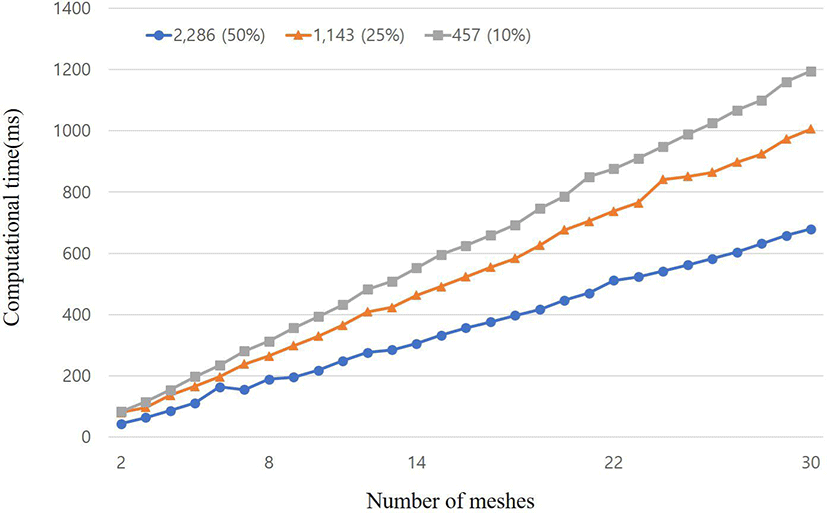
본 논문에서는 제안된 알고리즘의유효성을 실험하기 위해 다 양한표정을 가진얼굴 모델을 사용하였다. 각각의모델은정점이 4573개, 폴리곤이9108개로 모두동일했고메쉬의연결구조또한 동일하다. Figure 7(a)는 2개의 모델 사이에 블렌드쉐입을 적용 하여애니메이션이 진행되는 과정을 보여준다. Garland와 Heckbert [10]의 알고리즘(Algorithm 1)을 베이스쉐입과 타겟쉐입 각각에 대해 적용하면모델간에 일대일 대응관계가 더이상 성립하지 않아 선형보간이 제대로 적용되지 않는 반면(Figure 7(b)), 제시된 동시 단순화 알고리즘(Algorithm 2)을 적용하면 단순화후에도 모델간에 선형보간이 잘이루어진다(Figure 7(c)). Figure 8은 제시된 알고리즘의 확장성과 안정성을 보이기 위해서서로다른 3개의 얼굴 모델에 대하여 동일한 실험을 수행한 결과이다. Table 1은 메쉬의 수를 늘려가면서 동시 단순화에 소요되는시간을 측정한 결과이고, Figure 9은 Table 1의 결과를 가시화한결과이다. 실험 결과에서 보듯이 메쉬의 수에 따라 동시 단순화를 수행하는데 소요되는 시간은 선형적으로 증가하는 것을 볼 수있다.


6. 결론
본 논문에서 는다수의 삼각 메쉬에 대하여 동시 단순화를 수행하는 알고리즘을 제안하였다. 각각의 메쉬에 대하여에지 제거비용을 분석하여 모든 메쉬의 형상을 고려하여 확장된 에지 제거 정보를 설계하였으며, 이를 기반으로 모든 메쉬에 공통적으로적용될 수 있는 최적화된 에지 제거 순서를 결정하였다. 동일한 정점의 수와 연결 정보를 갖는다양한 얼굴 메쉬에 대하여 동시 단순화알고리즘을 적용하는 실험을 수행한 결과, 결과메쉬들은 모두 동일한 정점의 수와 연결 정보를 유지하면서 사용자가 지 정한 수준으로 단순화되는 결과를 보였다. 메쉬의 수를 최대 30 개까지 변화시키는 실험을 통해 제시된 기법의 안정성과 유효성 을입증하는 실험을 수행하였고, 이를 통해 동시 단순화 기법은 메쉬에 수에 따라 선형적으로 증가하는 시간 복잡도를 갖는다는 것을 실험적으로 보였다.
제시된 방법은 메쉬의 기하 정보만 고려하였기 때문에 텍스처 가 입혀진 모델에 대해서는단순화 결과가 어색하다. 또한 얼굴 모델 텍스처의 경우에는눈, 머리카락, 피부로 나뉘기 때문에 텍 스처경계부분에서알고리즘이잘적용되지않는다. 향후연구에 서는 텍스처 좌표 속성을 포함하고 있는 모델에 대해서 텍스처 경계부분이잘유지되도록동시단순화기법을확장할계획이다.