도메인 적응을 이용한 단일 파노라마 깊이 추정

이, 종협; 손, 형석; 이, 준용; 윤, 하은; 조, 성현; 이, 승용

doi:10.15701/kcgs.2020.26.3.61

J Korea Comput Graph Soc 2020; 26(3):61-68

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2020.26.3.61

Article

SINGLE PANORAMA DEPTH ESTIMATION USING DOMAIN ADAPTATION

이종협¹

, 손형석²

, 이준용³, 윤하은⁴

, 조성현⁵

, 이승용⁶^,^*

도메인 적응을 이용한 단일 파노라마 깊이 추정

Jonghyeop Lee¹

, Hyeongseok Son²

, Junyong Lee³, Haeun Yoon⁴

, Sunghyun Cho⁵

, Seungyong Lee⁶^,^*

Author Information & Copyright ▼

¹포항공과대학교

²포항공과대학교

³포항공과대학교

⁴포항공과대학교

⁵포항공과대학교

⁶포항공과대학교

¹POSTECH ljh5644@postech.ac.kr

²POSTECH sonhs@postech.ac.kr

³POSTECH junyonglee@postech.ac.kr

⁴POSTECH heyoon@postech.ac.kr

⁵POSTECH s.cho@postech.ac.kr

⁶POSTECH leesy@postech.ac.kr

^*corresponding author: Seungyong Lee/POSTECH(leesy@postech.ac.kr)

© Copyright 2020 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jun 19, 2020; Revised: Jun 22, 2020; Accepted: Jun 25, 2020

Published Online: Jul 01, 2020

Abstract

In this paper,we propose a deep learning framework for predicting a depth map of a 360° panorama image. Previous works use synthetic 360° panorama datasets to train networks due to the lack of realistic datasets. However,the synthetic nature of the datasets induces features extracted by the networks to differ from those of real 360° panorama images,which inevitably leads previous methods to fail in depth prediction of real 360° panorama images. To address this gap, we use domain adaptation to learn features shared by real and synthetic panorama images. Experimental results show that our approach can greatly improve the accuracy of depth estimation on real panorama images while achieving the state-of-the-art performance on synthetic images.

요약

본 연구에서는 360° 파노라마의 깊이 영상을 추정하는 딥 러닝 구조를 제안한다. 이전 연구들에서는 딥 러닝 네트워크를 학습 시키기 위해 렌더링 된 360° 파노라마 데이터셋을 사용했다. 하지만, 렌더링 된 파노라마 데이터 셋은 실제로 촬영된 파노라마 데이터 셋과 다르기 때문에,이전 연구들의 네트워크는 실제로 촬영된 파노라마에 대해선 깊이 영상을 정확히 추정할 수가 없었다. 이 문제를 해결하기 위해 본 연구에서는 도메인 적응을 사용해서 렌더링된 파노라마와 실제로 촬영된 파노라마가 공유하는 특징들을 네트워크가 학습하게 했다. 실험을 통해 우리의 방식이 렌더링된 파노라마에 대해선 우수한 성능을 유지 하면서 실제로 촬영된 파노라마에 대해서도 정확한 깊이 영상을 추정하는 것을 볼 수 있다.

Keywords: 깊이 추정; 딥러닝; 도메인 적응; 구형 파노라마; 단일 이미지

Keywords: depth estimation; deep learning; domain adaptation; spherical panorama; single image

1 Introduction

Estimating depth from a single image has been extensively studied due to its applicability to higher-level visual processing, such as generating 3D geometry [1], 3D rendering with object compositing [2], creating panoramas in other viewpoints [3], and scene understanding [4]. However, the majority of efforts on depth prediction has been focused on normal field-of-view (FoV) images, and depth estimation from 360° panorama images has been paid less attention despite the increasing popularity of 360° cameras.

For depth estimation from 360° panorama images, traditional approaches [5, 3] mostly use more than one panorama images, and rely on structure-from-motion (SfM) [6] and bundle adjustment with the plane sweeping algorithm [7]. With the recent advent of deep learning, single 360° panorama image-based depth estimation techniques have been introduced. Zioulis et al. [8] propose a supervised learning-based approach, in which they implement rectangular convolution filters for the robustness to geometric distortions in panorama images. Eder et al. [9] use two supervised decoders, one of which estimates a depth map, while the other predicts normal and boundary maps. Eder et al. [10] introduce deformed convolution kernels that dynamically change their shapes depending on the locations to effectively handle geometric distortions in panorama images. Zioulis et al. [11] introduce a self-supervised method to deal with error in training data. Thanks to the capability of deep learning, these methods can produce a plausible depth map even from a single image.

However, previous deep learning-based methods [8, 9, 10, 11] heavily rely on synthetic datasets as acquisition of real panorama images and depth maps is difficult. The most popular datasets for panorama image depth estimation include the SUMO [12] and 360D [8] datasets. The SUMO dataset consists of panorama images rendered from computer-generated 3D models, and their corresponding ground truth depth maps. The 360D dataset also consists of panorama images rendered from 3D models, and their corresponding depth maps. The 3D models used in the 360D datasets are either computer-generated or obtained by 3D scanning of real indoor environments.

Unfortunately, the synthetic nature of both datasets has fundamental limitations. While computer-generated 3D models may provide highly accurate depth information, panorama images rendered from them are often unrealistic and have different characteristics from real panorama images. On the other hand, 3D scanning may provide more realistic-looking panorama images, but suffer from 3D reconstruction errors, which lead to artifacts in panorama images and depth maps. Such unnatural characteristics of previous datasets introduce domain difference [13] between synthesized and real panorama images, which hinders the performance of learning-based depth estimation approaches. Fig. 1 shows the visual difference of synthetic and real panorama images.

Figure 1: Visual difference of synthetic and real panorama images.

Download Original Figure

In this paper, we propose a novel deep learning-based approach that estimates a depth map from a single 360° panorama image. In our approach, we use the 360D dataset [8] to train a convolutional neural network to predict a depth map from a single panorama image. However, to address the domain difference between synthesized and real images, we introduce domain adaptation into our framework. Specifically, for training the network, we utilize an additional dataset, SUN360 [14], which provides real 360° panorama images without ground truth depth maps. We also adopt an adversarial loss to learn features shared by synthetic and real panorama images so that the network can predict accurate depth maps from real panorama images even if it is trained on synthetic datasets. Additionally, we introduce a surface normal loss to suppress noise in predicted depth maps. Experimental results show that our approach outperforms previous approaches both on synthetic and real panorama images.

2 Our Approach

In this section, we describe the network architecture of our frame-work for depth map estimation from a single 360° panorama image, and how to train the network addressing the domain difference between synthetic and real data.

Our framework is built on top of Zioulis et al.’s framework [8], which is the state-of-the-art approach to depth estimation from a single panorama image. Fig. 2 shows our network architecture. Specifically, for our depth estimation network, we adopt the Rect-Net architecture [8], which is an encoder-decoder architecture. The network takes a single 360° panorama image obtained with equirectangular projection as input, and predicts its depth map. The network uses horizontally wide rectangular convolution filters of various sizes to deal with distortions of equirectangular projection. It also adopts dilated convolution to increase the size of receptive fields.

Figure 2: Our network architecture. Stride and activation function of a convolution layer are 1 and ELU, respectively if the layer does not have specific options. A rectangle is a feature map and the number under the rectangle is the number of channel. The feature map size of dark blue, orange and green rectangle are 512 × 256,256 × 128 and 128 × 64, respectively

Download Original Figure

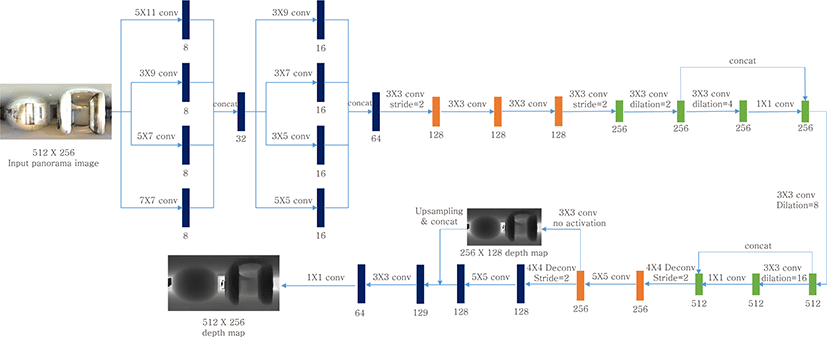
To train the depth estimation network, we utilize two different datasets: 360D [8] and SUN360 [14], each of which serves learning accurate depth estimation and domain adaptation, respectively. The 360D dataset provides 34,679 pairs of a synthetic panorama image and its ground truth depth map for training, and 1,298 pairs for testing. The SUN360 dataset provides real panorama images collected from the Internet without ground truth depth maps. The SUN360 panorama dataset is separated into two sets: indoor and outdoor. We randomly separated the indoor panorama images of SUN360 dataset into a training set of 10,598 images and a test set of 1,179 images.

To learn depth estimation, we minimize a loss function over the training set sampled from the 360D dataset, which is defined as:

L data = β depth L depth + β smooth L smooth + β normal L normal

(1)

where L_depth, L_smooth, and L_normal are data fidelity loss, smoothness loss, and surface normal loss, respectively. β_depth, β_smooth, and β_normal are their weights. L_depth makes it possible to learn depth estimation, while L_smooth encourages the depth estimation network to predict smooth depth maps. Following Zioulis et al. [8], we define L_depth and L_smooth as:

L depth = 𝔼 [‖ M (D G T − G (X S)) ‖ 2]

(2)

L smooth = 𝔼 [‖ M e M ∇ G (X S) ‖ 2]

(3)

where X_S and D_GT are a synthetic panorama image and its ground truth depth map, respectively. G indicates the depth estimation network, and G(X_S) is a depth map predicted from X_S. M is a binary mask of valid pixels in X_S, which is also provided by the 360D dataset. M^e is a binary mask to exclude pixels belonging to edges in D_GT as they often suffer from large errors caused by 3D scanning. The inclusion of this mask M^e is our own modification that was not a part of the original L_smooth proposed by [8]. We refer the readers to our supplementary material for the construction of M^e.

Without L_smooth, the network can still learn to predict accurate depth maps in terms of mean-squared-error (MSE), but the prediction results may suffer from high frequency noise, i.e., noisy surface normals. L_smooth can help avoid such noise as shown in [8], but it may harm the accuracy as it simply suppresses depth map gradients as will be shown in Sec. 3. To resolve this, we propose a novel loss function L_normal that encourages the surface normals of a predicted depth map to be similar to those of the ground truth depth map so that the predicted depth map has clean and accurate surface normals with less noise. Mathematically, we define L_normal as:

L normal = 𝔼 [‖ M e M (N (D G T) − N (G (X S))) ‖ 2]

(4)

where N is an operator that computes the surface normal map.

Training the depth estimation network using only Eq. (1) causes over-fitting to synthetic panorama images and performance degradation on real images due to the domain gap. To resolve this, we employ adversarial loss functions L_adv and L_D for domain adaptation, which are defined as:

L adv = 𝔼 [log (D (G (X R)))]

(5)

L D = 𝔼 [log (1 − D (G (X R)))] + 𝔼 [log (D (G (X S)))]

(6)

where X_R is a real panorama image. D is a discriminator network that takes a depth map produced by G and discriminates whether the depth map has been estimated from a synthetic panorama image or not. With Eq. (5), to deceive D for real images, G should produce depth maps with similar characteristics to the depth maps from synthetic images. On the other hand, Eq. (6) trains D to more accurately discriminate depth maps from real and synthetic panorama images. For the discriminator network D, we employ the same architecture as the encoder part of G, but with an additional fully connected layer at the end for binary classification.

Our total loss for training the depth estimation network G is then defined as:

L G = L data + α L adv

(7)

As constrained by both Eq. (1) and Eq. (5), G can preserve the high performance on the synthetic panorama images, while it can also produce similar quality results for real images. Consequently, our domain adaptation enables G to produce high-quality depth maps for any types of input images.

3 Results

We use Adam optimizer [20] to train the depth estimation and discriminator networks with a learning rate of 10^—4. We set [α, β_depth, β_smooth, β_normal, γ]=[10^—3, 1, 0.2, 0.4, 10^—4], where γ is the weight for L_D in Eq. (6). We first train the depth estimation network with only L_data for 65,000 iterations with batch size 10. Then we train the pretrained depth estimation network and discriminator network with L_G and L_D for 21,000 iterations with batch size 5.

We conduct an ablation study to verify the effect of each component of our framework. In our ablation study, we examine three variants of our model to verify the effect of the surface normal loss and the adversarial loss. The first model is a baseline model trained with only L_depth and L_smooth, which is the same model proposed by Zioulis et al. [8]. The second model is trained with L_depth, L_smooth and L_normal. Finally, the third model is trained with our final loss function in Eq. (7) with domain adaptation. Then, we qualitatively compare the results of the models on a real panorama image as real panorama images have no ground truth depth maps. Fig. 3 shows resulting depth maps of the three variants. In each depth map, bright pixels are far away, and dark pixels are close. As shown in Fig. 3(b), the baseline model produces noisy structures despite L_smooth. On the other hand, Fig. 3(c) shows that L_normal successfully suppresses noise even for the real image. However, the result still has large depth error as shown in the green box where the depth of an aisle is incorrectly estimated as very close. Finally, Fig. 3(d) shows that L_adv successfully improves the accuracy for the real image more accurately detecting the depth of the aisle.

Figure 3: Ablation study on a real panorama image from the SUN360 dataset [].

Download Original Figure

Figs. 4 and 5 show qualitative comparisons of our method with Zioulis et al. [8] on synthetic and real panorama images, respectively. Zioulis et al. [8]‘s model is trained with 360D [8] datasets. The input images in Figs. 4 and 5 are from the 360D and SUN360 datasets, respectively, and they are not used for training. For synthetic panorama images, both Zioulis et al.’s method and ours show reasonable results while our results are less noisy and sharper thanks to the surface normal loss. On the other hand, for real panorama images in Fig. 5, Zioulis et al.’s method produces a significant amount of errors due to the domain difference between the real and synthetic panorama images while our method still produces accurate results thanks to our domain adaptation. We refer the readers to the supplementary material for more examples.

Figure 4: Qualitative comparison on synthetic panorama images in the 360D dataset [].

Download Original Figure

Figure 5: Qualitative comparison on real panorama images in the SUN360 dataset [].

Download Original Figure

Finally, we quantitatively compare our method with previous state-of-the-art approaches on synthetic panorama images. We compare our method with two panorama image depth estimation approaches [8, 11] and five non-panorama image depth estimation approaches [15, 16, 17, 18, 19]. Zioulis et al. [8, 11]‘s two models are trained with 360D [8] datasets and a set of rendered panorama pairs made out of [21, 22, 23], respectively. [15] is trained with outdoor scenes such as KITTI [24] dataset, and other four non-panorama image depth estimation approaches [16, 17, 18, 19] are trained with NYUD-V2 [25] dataset. For quantitative comparison, we use the test set of the 360D dataset [8]. Since the non-panorama image methods are not trained for panorama images, it is unfair to directly compare our method with them. For a fair comparison, as Zioulis et al. [8] did, we divide a 360° panorama image into multiple subimages with a standard FoV by cube map projection and estimate a depth map for each image. Then, we merge the multiple depth maps into a panorama depth map using sphere projection. We use the final depth map for measuring the performance of the non-panorama image depth estimation methods. Table 1 shows that our method outperforms both panorama and non-panorama image depth estimation methods, which indicates that our approach also improves quantitative performance on synthetic panorama images while successfully reducing the domain gap between the synthetic and real panorama images.

Table 1: Quantitative comparison on the 360D dataset. ↓ and ↑ on the right-side of metric labels denote ‘smaller is better’ and ‘larger is better’, respectively. We refer the readers to our supplementary material for definitions of the metrics.

	Abs Rel ↓	Sq Rel ↓	RMS ↓	RMSlog ↓	δ < 1.25 ↑	δ < 1.25² ↑	δ < 1.25³ ↑
Godard et al. [15]	0.2552	0.9864	4.4524	0.5087	0.3096	0.5506	0.7202
Lainaet al. [16]	0.1423	0.2544	0.7751	0.2497	0.5198	0.8032	0.9175
Liu et al. [17]	0.1869	0.4076	0.9243	0.2961	0.424	0.7148	0.8705
Lee et al. [18]	0.3212	0.3511	1.0838	0.4109	0.4293	0.7389	0.8918
Yan et al. [19]	0.3841	0.5195	1.2677	0.4843	0.3406	0.6467	0.8405
Zioulis et al. [8]	0.0702	0.0297	0.2911	0.1017	0.9574	0.9933	0.9979
Zioulis et al. [11] λ_ratio = 0.6	0.1953	0.1531	0.6589	0.2614	0.6469	0.9212	0.9776
Zioulis et al. [11] λ_ratio = 0.8	0.1949	0.1457	0.6574	0.2591	0.6620	0.9180	0.9758
Zioulis et al. [11] λ_ratio = 1	0.1938	0.1444	0.6468	0.2573	0.6737	0.9159	0.9754
Zioulis et al. [11] supervised	0.1238	0.0693	0.4365	0.1723	0.8507	0.9679	0.9898
Ours	0.0708	0.0231	0.2498	0.1001	0.9614	0.9946	0.9982

Download Excel Table

4 Conclusion

In this paper, we presented a novel deep learning-based approach for depth map estimation from a single real panorama image by bridging the domain difference between real and synthetic panorama images using domain adaptation. As previous works rely on synthetic datasets, they are not guaranteed to accurately predict the depth from real panorama images. To address the lack of datasets with real panorama images for depth estimation, we introduced domain adaptation based on an adversarial loss for depth estimation from panorama images. We also proposed a surface normal loss to suppress noise in estimated depth maps. The quantitative and qualitative results demonstrate that our approach can effectively reduce the domain gap and accurately estimate the depth from synthetic panorama images.

Acknowledgement

본 논문은 과학기 술정 보통신부의 재원으로 정 보통신기술진흥센 터(SW 스타랩, IITP-2015-0-00174)와 차세대정보·컴퓨팅 기술개발사업 (NRF-2017M3C4A7066317)의 지원을 받아 수행된 연구 입니다.

References

[1].

K. Tateno, F. Tombari, I. Laina, and N. Navab, “Cnn-slam: Real-time dense monocular slam with learned depth prediction,” in Proc. CVPR, 2017.

[2].

K. Karsch, K. Sunkavalli, S. Hadap, N. Carr, H. Jin, R. da Fonte, M. Sittig, and D. Forsyth, “Automatic scene inference for 3d object compositing,” ACM TOG, vol. 33, no. 3, 2014.

[3].

J. Huang, Z. Chen, D. Ceylan, and H. Jin, “6-dof vr videos with a single 360-camera,” in Proc. IEEE VR, 2017.

[4].

X. Ren, L. Bo, and D. Fox, “Rgb-(d) scene labeling: Features and algorithms,” in Proc. CVPR, 2012.

[5].

S. Im, H. Ha, F. Rameau, H.-G. Jeon, G. Choe, and I.-S. Kweon, “All-around depth from small motion with a spherical panoramic camera,” in Proc. ECCV, 2016.

[6].

R. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, 2nd ed. USA: Cambridge University Press, 2003.

[7].

R. T. Collins, “A space-sweep approach to true multi-image matching,” in Proc. CVPR, 1996.

[8].

N. Zioulis, A. Karakottas, D. Zarpalas, and P. Daras, “Omnidepth: Dense depth estimation for indoors spherical panoramas,” in Proc. ECCV, 2018.

[9].

M. Eder, P. Moulon, and L. Guan, “Pano popups: Indoor 3d reconstruction with a plane-aware network,” in Proc. 3DV, 2019.

[10].

M. Eder, T. Price, T. Vu, A. Bapat, and J. Frahm, “Mapped convolutions,” ArXiv, 2019.

[11].

N. Zioulis, A. Karakottas, D. Zarpalas, F. Álvarez, and P. Daras, “Spherical view synthesis for self-supervised 360° depth estimation,” in Proc. 3DV, 2019.

[12].

D. Huber and L. Tchapmi, “The sumo challenge,” The 2019 SUMO Workshop 360° Indoor Scene Understanding and Modeling.

[13].

J. Hoffman, E. Tzeng, T. Park, J.-Y. Zhu, P. Isola, K. Saenko, A. A. Efros, and T. Darrell, “CyCADA: Cycle-consistent adversarial domain adaptation,” in Proc. ICML, 2018.

[14].

J. Xiao, K. A. Ehinger, A. Oliva, and A. Torralba, “Recognizing scene viewpoint using panoramic place representation,” in Proc. CVPR, 2012.

[15].

C. Godard, O. M. Aodha, and G. J. Brostow, “Unsupervised monocular depth estimation with left-right consistency,” in Proc. CVPR, 2016.

[16].

I. Laina, C. Rupprecht, V. Belagiannis, F. Tombari, and N. Navab, “Deeper depth prediction with fully convolutional residual networks,” in Proc. 3DV, 2016.

[17].

F. Liu, C. Shen, G. Lin, and I. D. Reid, “Learning depth from single monocular images using deep convolutional neural fields,” IEEE TPAMI, vol. 38, no. 10, pp. 2024-2039, 2016.

[18].

J. H. Lee, M. Han, D. W. Ko, and I. H. Suh, “From big to small: Multi-scale local planar guidance for monocular depth estimation,” ArXiv, 2019.

[19].

W. Yin, Y. Liu, C. Shen, and Y. Yan, “Enforcing geometric constraints of virtual normal for depth prediction,” in Proc. CVPR, 2019.

[20].

D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” in Proc. ICLR, 2015.

[21].

I. Armeni, S. Sax, A. R. Zamir, and S. Savarese, “Joint 2d-3d-semantic data for indoor scene understanding,” ArXiv, vol. abs/1702.01105, 2017.

[22].

A. X. Chang, A. Dai, T. A. Funkhouser, M. Halber, M. Nießner, M. Savva, S. Song, A. Zeng, and Y. Zhang, “Matterport3d: Learning from rgb-d data in indoor environments,” 2017 International Conference on 3D Vision (3DV), pp. 667676, 2017.

[23].

S. Song, F. Yu, A. Zeng, A. X. Chang, M. Savva, and T. A. Funkhouser, “Semantic scene completion from a single depth image,” Proc. CVPR, pp. 190-198, 2016.

[24].

A. Geiger, P. Lenz, and R. Urtasun, “Are we ready for autonomous driving? the kitti vision benchmark suite,” 2012.

[25].

N. Silberman, D. Hoiem, P. Kohli, and R. Fergus, “Indoor segmentation and support inference from rgbd images,” in Proc. ECCV, 2012.

[26].

J. Hu, M. Ozay, Y. Zhang, and T. Okatani, “Revisiting single image depth estimation: Toward higher resolution maps with accurate object boundaries,” 2018.

[27].

Y.-C. Su and K. Grauman, “Learning spherical convolution for fast features from 360° imagery,” ArXiv, vol. abs/1708.00919, 2017.

[28].

A. Handa, V. Patraucean, S. Stent, and R. Cipolla, “Scenenet: An annotated model generator for indoor scene understanding,” 2016 IEEE International Conference on Robotics and Automation (ICRA), pp. 5737-5743, 2016.

[29].

I. Armeni, O. Sener, A. R. Zamir, H. Jiang, I. K. Brilakis, M. Fischer, and S. Savarese, “3d semantic parsing of large- scale indoor spaces,” 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1534-1543, 2016.

[30].

I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. C. Courville, and Y. Bengio, “Generative adversarial nets,” in NIPS, 2014.