안정적이고 이방성한 빙결 모델링을위한 암시적 비압축성 유체와 얼음 입자간의 상호작용 기법

김, 종현

doi:10.15701/kcgs.2020.26.5.1

J Korea Comput Graph Soc 2020; 26(5):1-13

pISSN: 1975-7883, eISSN: 2383-529X

DOI: https://doi.org/10.15701/kcgs.2020.26.5.1

Article

안정적이고 이방성한 빙결 모델링을위한 암시적 비압축성 유체와 얼음 입자간의 상호작용 기법

김종현 ¹ ^, ^*

Stable Anisotropic Freezing Modeling Technique Using the Interaction between IISPH Fluids and Ice Particles

Jong-Hyun Kim ¹ ^, ^*

Author Information & Copyright ▼

¹강남대학교 jonghyunkim@kangnam.ac.kr

¹Kangnam University

^*Jong-Hyun Kim/Kangnam University(jonghyunkim@kangnam.ac.kr)

© Copyright 2020 Korea Computer Graphics Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Sep 10, 2020; Revised: Oct 19, 2020; Accepted: Oct 23, 2020

Published Online: Dec 31, 2020

요약

본 논문에서는 흐르는 물에 의해 빙결 시뮬레이션 되어 방향성이있는 얼음 형태를 안정적으로 모델링 할 수 있는 새로 운 방법을 제시한다. 제안하는 얼음 모델링 프레임워크는 빙결 시뮬레이션에서 중요한 얼음의 성장 방향에 점성이있는 유체의 흐름을 고려한다. 물 시뮬레이션 해법은 암시적 비압축성 유체 시뮬레이션에 새로운 점성 기법을 적용한 방법을 이용하고, 얼음의 방향과 글레이즈(Glaze) 효과는 제안하는 비등방성한 빙결 해법을 이용한다. 물 입자가 얼음 입자로 상태변화하는 조건은 습도와 물의 흐름에 따른 새로운 에너지 함수에 따라 계산된다. 습도는 오브젝트 표면의 가상 수막 (Virtual water ﬁlm)으로 근사되며, 유체의 흐름은 얼음의 성장 방향을 가이드하기 위해 우리의 비등방성한 빙결 해법에 통합된다. 결과적으로 점성이있는 물의 흐름 방향에 따라 글레이즈와 방향성 있는 빙결 시뮬레이션 결과를 안정적으로 보여준다.

Abstract

In this paper, we propose a new method to stable simulation the directional ice shape by coupling of freezing solver and viscous water flow. The proposed ice modeling framework considers viscous fluid flow in the direction of ice growth, which is important in freezing simulation. The water simulation solution uses the method of applying a new viscous technique to the IISPH(Implicit incompressible SPH) simulation, and the ice direction and the glaze effect use the proposed anisotropic freezing solution. The condition in which water particles change state to ice particles is calculated as a function of humidity and new energy with water flow. Humidity approximates a virtual water ﬁlm on the surface of the object, and fluid flow is incorporated into our anisotropic freezing solution to guide the growth direction of ice. As a result, the results of the glaze and directional freezing simulations are shown stably according to the flow direction of viscous water.

Keywords: 빙결 시뮬레이션; 얼음 형태; 암시적 비압축성 유체; 얼음의 글레이즈; 얼음의 비등방성한 성장 방향

Keywords: Freeze simulation; Icicle shape; Implicit incompressible SPH; Glaze of ice; Anisotropic growth direction of ice

1. 서론

영화나 게임 등 다양한 가상현실(Virtual Reality, VR) 콘텐츠에 서 빙결 현상은 다양한 형태로 활용되고 있다 : “The Day after Tomorrow” (2004), “The Last Airbender” (2010), “The Huntsman: Winter’s War” (2016). 일반적인 고드름처럼 중력에 의해서 아 래방향으로만 성장하는 얼음 형태가 아닌, VR콘텐츠에서는 극한의 겨울을 표현하기 위해 대부분의장면에서 얼음의 형태 는 물체의 표면이나 물 또는 바람과 같은 특정 방향으로 휘어 지거나 비틀어진다. 컴퓨터 그래픽스 분야에서는 얼음의 생성 과 성장을 나타내기 위한 연구들이 많이 진행되었다. Im 등은 불투명한 얼음의 내부를 표현할 수 있는 기술을 제안했고 [1], Kharitonsky와 Gonczarowski는 물리 기반 시뮬레이션을 활용 하여 고드름의 생성과 성장 기술을 제안했다 [2]. Kim 등 [3]과 Gagnon과 Paquette는 [4] 절차적 방법을 사용하여 물체 표면에 표현되는 글레이즈 효과와 고드름 생성 기술을 제안했다. 이 기술은 천천히 떨어지는 물방울에 의해서 생성되는 고드름과 글레이즈 효과를 표현하는데 중점을 두었기 때문에 특정 장면 에서만 활용이 가능하며, 물과 얼음의 상호작용에 의해 얼음 이 생성되고 자라나는 특징을 표현하는데는 어려움이있다.

본 논문에서는 물의 흐름을 고려하여얼음의 형태를 모델링 하는 물리 기반 시뮬레이션 기법을 제안한다. 우리의 방법은 Im 등의 방법과 [5] 유사하게 온도 기반 모델이 아닌, 결정화 (Crystallization) 기반 상태변화 모델을 활용한다. 우리의 방법 은 0도 이하의 온도에서는 액체를 유지하지만, 차가운 표면과 충돌할 때 빠르게 얼어 붙는 과냉각 동결(Supercooled water) 현상에서 영감을 얻었다 (Figure 1 참조). 또한, 물이 흐르면서 발생하는 빙결의 특성을 좀 더 정확하게 표현하기 위해 유체 흐름에 따라 얼음의 성장 방향을이방성(Anisotropic)하게 모델 링한다. 빙결을 표현하려는 이전접근법들에서는 고체의 표면 을 흐르면서 얼어붙는 현상을 표현하지 못하고, 물과 고체의 충돌에 의해 발생하는 외력때문에 입자의 흩날리는 움직임은 빙결 모델링의 안정성을 떨어뜨리며, 빙결 모델링 품질에도 영향을 미친다. 또한, 가지처럼 뻗어나가면서 얼어붙는 얼음 의 성장 방향을 계산함에 있어서 등방성 커널은 정확한 성장 방향을 표현하는데 한계가 있다 [5]. 중력에 의해한방울 한방 울 떨어지는 물방울로는 중력에 의한 방향만을 고려한 얼음 의 형태가 나타나는 반면, 본 논문에서 제안하는 기술은 오브 젝트 또는 외력과의 충돌로 인해 물의 흐름이 동적으로 변화 함에 따라 얼음을 이방성하게 생성하거나 성장시킬 수 있다. 따라서 물의 흐름에 따라 얼음의 성장을 함께 표현할 수 있다 는 장점이 있다. 뿐만 아니라 물이 급속히 얼어 붙는 현상을 표현할 수 있다.

Figure 1: Cooling phenomenon of water with the supercooled water.

Download Original Figure

2. 관련 연구

본 논문에서 제안하는 방법과 유사한 얼음 및 빙결 시뮬레이 션 기법들과 눈 시뮬레이션에 관련된 다양한 연구들에 대해서 살펴본다.

2.1 얼음 및 빙결 시뮬레이션

물리 기반 시뮬레이션 분야에서 얼음의 생성 및 성장과 관련된 연구들은 꾸준히 발표되었다. Kim 등은 작고 얇은 물 입자의 결정화(Crystallization)를 통해 얼음의 성장을 표현함으로써 평 평하거나 곡면인 부분에서 자라나는 서리(Frost) 현상을 사실 적으로 표현했다 [6]. Im 등 [1]과 Nishino 등은 [7] 얼음 내부에 표현되는 불투명한 영역과같은 얼음의 세부적인 특징을 표현 할 수 있는 방법을 제안했다. Kim 등은 얼음에 충격이 가해졌 을 때 얼음 표면에 표현되는 균열과 흠집을 모델링하는 방법을 제안했다 [8]. Kharitonsky와 Gonczarowski는 물방울의 물리적 모델을 고려한 고드름의 성장을 시뮬레이션함으로써 열역학 을 통한 고드름의 성장과 형태를 사실적으로 표현했다 [2].

Kim 등은 기존의 접근법과는 다르게 Stefan 문제를 풀어냄 으로써 고드름의 성장을 표현했다 [3]. 이 방법은 다수개의 고 드름을 동시에 표현함으로써 고드름이 서로 합쳐지는 듯한 형 상을 사실적으로 표현했지만, 시뮬레이션 계산양이 크다는 단 점이 있다. Gagnon와 Paquette는 사용자가 얼음 성장 시뮬레 이션을 쉽게 제어할 수 있는 절차적 방법을 제안했고 [4], 이 를 통해 얼음의 형태 뿐만 아니라 글레이즈 효과도 사용자가 의도하는 형태에 맞게 모델링이 가능했다. 앞에서 언급한 접 근법들과 비교했을 때, 이들의 방법은 빠르게 고드름을 생성 하지만, 단일 형태의 고드름만 표현할 뿐, 다수개의 고드름에 서 표현되는 병합을 표현하기에는 충분하지 않다. Ishikawa 등 은 글레이즈 효과와 고드름의 생성 방식을 기반으로 물방울이 중력에 의해 떨어지면서 빙결되는 시뮬레이션 기법을 제안했 다 [9]. 언급한 모든 방법은 중력에 의해 물방울이 아래 방향으 로만 천천히흐른다는 전제 조건하에얼음 형성을 모델링했기 때문에, 다양한 장면에서 표현되는 빙결 형태를 모델링하기에 는 한계가 있다.

몇몇 연구들은 흐르는 물에서 빙결을 표현하려고 노력했 다 [10]. 이 방법은 공기 방울의 확산을 기반으로 불투명한 빙결 현상을 표현했지만, 고드름이나 글레이즈 효과는 표현 할 수 없다. Iwasaki 등은 입자 기반으로 용해(Melting)와 빙결 (Freezing) 효과를 표현할 수 있는 방법을 제안함으로써 [11], 얼음 표면에 생성되는 얼음 스파이크(Ice spikes)를 표현했지 만, 대분의 결과가 용해에만 초점이 맞춰져 있어서 병결 효과 에는 적용이 힘든 접근법이다. Wicke 등은 암시적 연결성(Implicit connectivity)을 기반으로 다양한 재질을 시뮬레이션 했으 며 [12], 뿐만 아니라 온도 전달 방법을 사용하여 흐르는 물에 서 빙결로 인해 얼음이 생성되는 결과를 만들어냈다. Makkonen와 Takahashi는 관찰을 기반으로한 얼음 성장 이론 모델을 제안했지만 [13, 14], 이론을이산화하고 구현하는 과정에서의 알고리즘을 제안하지 않아서 직접적으로 시뮬레이션하거나 시각화를 하기에는 충분하지 않다.

2.2 눈 시뮬레이션

연속체 역학을이용하여얼음 뿐만 아니라 눈을 시뮬레이션하 려는 접근법들이 많이 발표되었으며, 이러한 시뮬레이션 접근 법은 탄소성 눈 모형(Elastoplastic snow models)을 표현하는데 사용되었다 [15]. Stomakhin 등은 컴퓨터 그래픽스 분야에서 처음으로 MPM(Material point method)를 도입하여 눈 시뮬레 이션 기법에 활용했으며 [16], 그 뒤로 위상 변화를 처리하기 위해 다양한 방법으로 MPM방법이 확장되었다 [17, 18, 19, 20, 21]. 최근에 Han 등은 눈과 머리카락 사이에서 표현되는 마찰 접촉을 MPM 프레임워크에서 풀어냈다 [22].

MPM 이외도 눈 역학을 시뮬레이션하는데 사용되는 다 른 이산화 기법도 있다. Wong과 Fu는 인터랙티브한 시뮬레 이션 환경에서 눈을 표현하기 위해 눈 입자와 스프링 역학 에 DEM(Discrete element method)를 적용하여 사용한 기법이 다 [23]. Mukai 등은 확장된 DEM방법을 사용하여 지붕에서 눈이 갈라지고 내리는 것을 시뮬레이션 했고 [24], Dagenais 등은 PBD(Position based dynamics)와 레벨셋(Level-set)을 활용 하여 눈 동작을 시뮬레이션 했다 [25]. Takahashi와 Fujishiro는 SPH(Smoothed particle hydrodynamics) 기반의 유동을 활용하 여 눈의 움직임을 모델링했다 [26]. Abdelrazek 등은 빙햄 점도 모델(Bingham viscosity model)을 사용하여 눈사태 시뮬레이션 기법을 제안했고 [27], Goswami 등은 GPU를 활용하여 실시간 으로 눈의 움직임을 표현했다 [28].

3. 제안하는 프레임워크

본 논문에서 제안하는 프레임워크는 유체 시뮬레이션 단계와 빙결 시뮬레이션 단계로 구성된다. 유체 시뮬레이션 단계에서 는 암시적 비압축 유체(Implicit incompressible SPH) [29] 기반 해법에 따라 유체의 움직임, 유체-고체 상호작용, 표면장력 및 접착력을 계산한다. 우리는 고체 메쉬의 정점, 에지, 페이스에 각각 경계 입자(Boundary particle)를 생성하고 [30], 이를 이용 하여 유체와 고체의 상호작용을 계산한다 [31]. 접착력과 표면 장력은 He 등의 방법을 사용하였으며 [32], 얼음의 글레이즈와 곡선형 빙결 형태를 안정적으로 표현하기 위해 점성 기반 유 체를 모델링한다. 본 논문의 핵심 주제는 안정적으로 얼음의 생성과 성장을 시뮬레이션하는 것이다.

실제로 과냉각 동결(Supercooled water) 과정은 본 논문에서 의 동기부여 현상이며, 이러한 현상은 중력에 의해 아래 방향 으로만 자라나는 얼음의 형태를 벗어나 좀 더 복잡한 빙결 형 태를 쉽게 모델링할 수 있게 한다. 물리적으로 과냉각수는 이 미 0도 미만의 온도에 있으므로 온도 변화가 아닌, 분자 간의 결정화에 의해 빙결이 진행된다. 우리가 다루고 있는 유체는 과냉각수라고가정하였으며, 유체가 얼음으로 상태변화를 하 기 위한 결정화 단계는 Im 등이 제안한핵 생성 에너지(Nucleation energy)에 기초하여 새롭게 제안한다 [5].

3.1 암시적 비압축 기반 유체 시뮬레이션

암시적 비압축 유체(Implicit incompressible SPH, IISPH) 시뮬 레이션은 입자 기반 유체에서 발생하는 비압축 문제를 개 선하기 위한 방법 중 하나이다. IISPH는 연속 방정식(Continuity equation)의 LHS(Left hand side)은 기본적인 SPH기법의 RHS(Right hand side)와 오일러 방법의 1차 정확도를 통해 다 음과같이이산화시킬 수 있다 : $D ρ D t = ρ ∇ ⋅ v$ . 결과적으로 연속 방정식은 다음과같이 다시 쓸 수 있다 (Equation 1 참조).

ρ i (t + Δ t) − ρ i (t) Δ t = ∑ j ∈ S (i) m j v i j (t + Δ t) ∇ W i j

(1)

여기서 S (i)는 i번째 입자에 해당하는 인접 입자들이며, ρ_i와 m_i는 i번째 입자의 밀도와 질량, v_ij는 i와 j번째 입자의 속도 차이이다 : v_ij = v_i − v_j. W 는 3차 스플라인 보간법으로 다음 과같이 계산한다 (Equation 2 참조).

W (q, h) = 5 14 π h 2 {(2 − q) 2 − 4 (1 − q) 3, 0 ≤ q < 1 (2 − q) 3, ≤ q < 2, 0, q ≥ 2

(2)

여기서 h는 커널 함수의 길이이고, q는 $| r | h$ 로 정의하며, r은 다 음과같다 : r = x_ij. 본 논문에서 시뮬레이션 도메인의 반지름 은 h에 비례하도록 kh로 계산했으며, k는 2로 설정했다. W_ij는 W |_{r=x_ij} 로 정의하고, ▽_i는 x_i에 대한 기울기로(i.e. $∂ ∂ x i$ ), 본 논문에서는 ▽W_ij로 쓰도록 한다. 또한, v_ij와 유사하게 x_ij는 x_i − x_j를 의미한다. Equation 1에서 v_ij (t + Δt)와 ρ_i (t + Δt) 는 미지수이지만, 연속 방정식의 비압축성을 만족시키기 위해 다음과 같은 조건으로 만족 시키고(ρ_i (t + Δt) =ρ₀), 향후 이 수식을 기반으로 압력에 대한 방정식을 도출한다.

뉴턴의 제2법칙은 i번째 입자의 위치에서 작용하는 힘에 의 한 압력과 비압력을 명시적으로 표현하는데 사용된다. 그렇 게하기 위해, F_i에 대한 RHS는 오일러 방법의 1차 정확도 이 용하여 계산하고 $F i = m i D v i D t$ , F_i는 압력과 비압력 구간으로 구분하여 계산한다 (Equation 3 참조).

F p (t) + F n p (t) = m i v i (t + Δ t) − v i (t) Δ t

(3)

여기서 F^p와 F^np는 압력과 비압력에 대한 힘을 나타낸다. 위 수식을 이용하여 속도를 다음과 같이 새로 정의한다 (Equation 4 참조).

v i (t + Δ t) = v i (t) + F i, l p (t) + F i, l n p m i Δ t

(4)

속도는 다음과 같이 힘의 압력 기여도에 따라 두 가지 구성 요소로 나뉜다 (Equation 5 참조).

v i, l + 1 = (v i, l + F i, l n p m i Δ t) + F i, l p m i Δ t = v i, l n p + v i, l + 1 p

(5)

여기서 $v i, l n p$ 와 $v i, l p$ 는 각각 $v i, l n p = v i, l + F i, l n p m i, v i, l p = F i, l p m i Δ t$ 를 이용하여 계산하고, 아래 첨자 l과 l +1은 시간 t와 t + Δt에서 각각 이산화된 값을 나타낸다. IISPH는 Chorin의 2단계 프로젝 션 알고리즘과 유사하다 : 1) 중간속도 u^*는 이전 시간(Previous time-step)에서의 점성 및 속도와 관련이 있으며, 2) 새로운 속 도는 새로운 시간(New time-step)에서의 압력과 중간속도와 관 련이 있다. 본 논문에서 $v i, l n p$ 는 Chorin의 투영법에서 중간속도 u^*와 유사하며, $v i, l + 1 p$ 는 Navier-Stokes 방정식의 압력에 대한 기울기에 영향을 준다. Chorin의 투영법에서 압력 수식은 새 로운 시간에서의 속도에 대해 Divergence-free조건을 적용함으 로써 얻을 수 있다. 그러나 IISPH에서의 압력 수식은 새로운 시간인 t + Δt에서의 밀도에 대한 비압축성을 적용함으로써 얻을 수 있다. Equation 1에 의해서 밀도를 압력 부분과 비압력 부분으로 나누고, 중간속도인 $v i, l n p$ 로부터 중간 밀도인 $ρ i, l n p$ 를 계산할 수 있다 (Equation 5 참조).

ρ i, l n p = ρ i, l + Δ t ∑ j ∈ S (i) m j v i j, l n p ∇ W i j

(6)

Equation 6에 Equation 5를 넣으면 결과적으로 Equation 7과 같이유도된다.

ρ i, l + 1 = ρ i, l + Δ t ∑ j ∈ S (i) m j v i j, l + 1 ∇ W i j

(7)

ρ i, l + 1 − ρ i, l n p = Δ t ∑ j ∈ S (i) m j (v i j, l + 1 − v i j, l n p) ∇ W i j

(8)

여기서 ρ_i,l는 ρ_i,l = Σ_jm_jW_ij이고, 비압축성을 유지하려면 수치 정확도의 한계 내에서 ρ_i,l₊₁ = ρ₀를 만족시켜야 한다. 또한, Equation 5와 $v i j, l + 1 p$ 를 이용하면 위 수식을 좀 더 단순한 형태로 만들 수 있고, 이 방정식을이용하여압력 수식을 암시 적으로 표현할 수 있다 (Equation 8 참조).

ρ 0 − ρ i n p = Δ t ∑ j ∈ S (i) m j v i j, l + 1 p ∇ W i j = Δ t ∑ j ∈ S (i) m j (F i j, l + 1 p m i Δ t) ∇ W i j = Δ t 2 ∑ j ∈ S (i) m j (F i, l + 1 p − F j, l + 1 p) ∇ W i j .

(9)

향후, 위 수식을 통해 압력을 계산한다. Eqaution 9에 Eqaution 6인 $ρ i n p$ 를 넣으면 Eqaution 9를 아래와 같이 다시 쓸 수 있다 (Eqautions 10과 11 참조).

ρ 0 − (ρ i, l + Δ t ∑ j ∈ S (i) m j v i j, l n p ∇ W i j) = Δ t 2 ∑ j ∈ S (i) m j (F i, l + 1 p m i − F j, l + 1 p m i) ∇ W i j

(10)

ρ 0 − ρ i, l − Δ t ∑ j ∈ S (i) m j (v i j, l + (F i, l n p m i − F j, l n p m j) Δ t) ∇ W i j = Δ t 2 ∑ j ∈ S (i) m j (F i, l + 1 p m i − F j, l + 1 p m j) ∇ W i j

(11)

여기서 $v i, l n p = v i, l + F i, l n p m i Δ t$ 는 LHS를 단순화 하는데 사용되며, 운동량이 보존되는 압력에 대한 힘은 다음과 같이 계산한다 (Equation 12).

F i, l + 1 p = − m i ∑ j ∈ S (i) m j (p i, l + 1 ρ i, l 2 + p j, l + 1 ρ j, l 2) ∇ W i j

(12)

그리고, $F i, l n p$ 은 다음과같이 계산한다 (Equation 13 참조).

F i, l n p = m i ∑ j ∈ S (i) m j ∏ i j

(13)

∏ i j = − (μ i + μ j) x i j ∇ W i j ρ i j − 2 (x i j 2 + є h ¯ i j 2) v i j, l,

(14)

여기서 $h ¯ i j$ 는 다음과 같이 계산되며 : $h ¯ i j = (h i + h j) 2$ , 이 값은 커널의 반지름에 영향을 받고, $ρ ¯ i j$ 는 다음과 같이 계산한다 : $ρ ¯ i j = (ρ i + ρ j) 2$ .

Equation 11에서 LHS의 변수 값은 알고 있으며, RHS는 Equation 12의 단순화 버전을 통해 좀 더 간략화할 수 있다 (Equation 15 참조).

Δ t 2 F i, l + 1 p m i = − Δ t 2 ∑ k ∈ S (i) m k (p i, l + 1 ρ i, l 2 + p k, l + 1 ρ k, l 2) ∇ W i k = (− Δ t 2 ∑ k m k ρ i, l 2 ∇ W i k) p i, l + 1 + (∑ k ∈ S (i) − Δ t 2 p k, l + 1 m k ρ k, l 2 ∇ W i k) = d i i p i, l + 1 + ∑ k ∈ S (i) d i k p k, l + 1,

(15)

여기서 d_ik는 $d i k = − Δ t 2 m k ρ k, 1 2 ∇ W i k$ 이며, 이 수식을 비슷하 게 $Δ t 2 F j, l + 1 p m j$ 도 다시 쓸 수 있다. Equation 15를 사용함으로써 Equation 11의 RHS는 다음과 같이 쓸 수 있다 (Equation 16 참 조).

R H S = ∑ j ∈ S (i) m j ((d i i p i, l + 1 + ∑ k ∈ S (i) d i k p k, l + 1) − (d j j p j, l + 1 + ∑ k ∈ S (j) d j k p k, l + 1 ︸ *)) ∇ W i j

(16)

위 수식에서 i번째 입자에 대한 기여도는 마지막 항(symbol *)에서 추출되며, 다음과같이 쓸 수 있다 (Equation 17 참조).

∑ k ∈ S (j) d j k p k, l + 1 = ∑ k ∈ S (j), k ≠ i d j k p k, l + 1 + d j i p i, l + 1

(17)

위 수식은자코비 반복법과같은 수치해법으로 솔루션을 도 출 해야 되기 때문에, Equation 11의 RHS는 다음과 같이 다시 쓴다 (Equation 18와 19 참조).

R H S = ∑ j ∈ S (i) (d i i p i, l + 1 + ∑ k ∈ S (i) d i k p k, l + 1 − (d j j p j, l + 1 + d j i p i, l + 1 + ∑ k ∈ S (j), k ≠ i d j k p k, l + 1)) ∇ W i j = ∑ j ∈ S (i) p i, l + 1 (d i i − d j i) m j ∇ W i j + ∑ j ∈ S (i) m j (∑ k ∈ S (i) d i k p k, l + 1 − d j j p j, l + 1 − ∑ k ∈ S (j), k ≠ i d j k p k, l + 1) ∇ W i j

(18)

∴ R H S = a i i p i + ∑ k ∈ S (i) (∑ k d i k p k, l + 1 − d j j p j, l + 1 − ∑ k ∈ S (j), k ≠ i d j k p k, l + 1) ∇ W i j

(19)

여기서 a_ii,d_ii,d_ik는다음과같이 정의된다 (Equation 20 참조).

a i i = ∑ j ∈ S (i) (d i i − d j i) m j ∇ W i j d i i = − Δ t 2 ∑ k ∈ S (i) m k ρ i, l 2 ∇ W i k d i k = ∑ k ∈ S (i) − Δ t 2 p k, l + 1 m k ρ k, l 2 ∇ W i k

(20)

반복적인 수치해법으로 압력을 업데이트하기 위해서는 Equation 11의 RHS를 Equation 19로 대체하여 계산한다 (Equation 21 참조).

p i r = ξ a i i

(21)

ξ = ρ 0 − ρ i n p − ∑ j ∈ S (i) m j (∑ k ∈ S (i) d i k p k, l + 1 r − d j j p j, l + 1 r − 1 − ∑ k ∈ S (j), k ≠ i d j k p k, l + 1 r − 1) ∇ W i j)

(22)

여기서 위첨자 r − 1과 r은 각각 이전과 새로운 반복 값을 나 타내고, $ρ i n p$ 는다음과같이 정의된다 (Equation 23 참조).

ρ i n p = ρ i, l + Δ t ∑ j ∈ S (i) m j (v i j, l + (F i, l n p m i − F j, l n p m j) Δ t) ∇ W i j

(23)

위 수식에서 $p i, l + 1 r$ 의 잔차(Residual)가 충분히 작을 때까 지 이 방정식을 반복적으로 풀어야 한다. 본 논문에서는 SOR(Successive over relaxation)방법을 사용했으며, 아래와 같 은 방법을 이용하여 반복법의 수렴률을 개선시켰다 (Equation 24 참조).

p i r = (1 − w) p i r − 1 + w p i r

(24)

여기서 w는 실험적으로 찾은 값이며, 본 논문에서는 0.8로 설 정했다. Equation 21을 기반으로 계산한 반복적인 수치해법으 로 압력을 계산할 수 있으며, 이 값은 Equation 15에서 $F i, l + 1 p$ 를 계산하기 위해 사용된다. 또한, $F i, l n p$ 는 Equation 13를 이용 하여 계산한다. 이 두개의 값은 새로운 속도를 계산하기 위해 Equation 3에서 사용된다. 입자의 위치인 x_i는 1차 오일러 방 식을 사용하여 업데이트한다. Figure 2는 IISPH 기반의 유체 시뮬레이션 결과이며, 우리는 이 유체 해법을 빙결 시뮬레이 션과 통합시켜 새로운 얼음 성장 결과를만든다.

Figure 2: Water simulations based on IISPH.

Download Original Figure

3.2 이방성한 빙결 시뮬레이션

3.2.1 고체 표면의 가상 수막

얼음 성장은 습식와 건식 성장에 따라 표현되며, 여기서 이 두 가지 속성은 물이 얼음으로 변화되는 상태변화 속도에 영향을 주는 결빙비(Freezing fraction)에 영향을 받는다. 습도가 증가 함에 따라 결빙비가 감소하고, 젖은 양인 습식의 성장에 따라 물이 얼음으로 빙결된다 [14]. 건식 성장 과정에서 유체 입자는 오브젝트와 충돌한 직후 얼음으로 변환된다. 습식 성장 과정 에는 유체 입자가 오브젝트 표면에 흐르고, 얼음이 축점됨에 따라 수막을 형성한다. 수막을 형성하는데 있어서 레벨셋을 이용한 경우도 있지만 [33], 이러한 접근법은일반적으로 계산 비용이 높으며 입자 기반 시뮬레이션에는 적합하지 않기 때문 에 수막에 대한 시뮬레이션을 표현할 수 없다.

본 논문에서는 고체 입자에 가상 수막을 추가하여 효율적 으로 수막을 표현한다. 가상 수막인 Γ를 생성하는 과정에서 고체 입자는 인접한 유체 입자들에 대한 가상 질량을 고려하 여, 결과적으로 유체 입자로부터 전달된 질량의 양은 결빙비 인 α^ice|solid를 고려하여 계산된다 (Equation 25 참조).

Γ t i c e | s o l i d = Γ t − Δ t i c e | s o l i d + Δ Γ i c e | s o l i d Δ Γ i c e | s o l i d = α i c e | s o l i d ∑ j m f l u i d η W (x i c e | s o l i d − x f l u i d) η = 1 − Γ t − Δ t i c e | s o l i d Γ max

(25)

여기서 ΔΓ^ice|solid는 유체 입자로부터 얻은 가상 질량의 양이 다. $Γ t i c e | s o l i d$ 와 $Γ t − Δ t i c e | s o l i d$ 는 현재와 이전 시간에서의 가장 수막 의 양이며, α^ice|solid와 m^fluid는 고체 입자의 결빙비와 유체 입 자의 질량이다. η는 얼음과 유체 입자의 가상 수막에 대한 비 율이다. 결과적으로 유체 표면의 수막은 유체 입자의 질량을 초과할 수 없으며, 본 논문에서 Γ_max는 유체 입자의 질량으로 설정하였다.

3.2.2 이방성한 얼음의 성장 방향

얼음은 중력에 의해서 주로 가로보다는 세로 방향으로 빠르 게 성장한다. 일반적으로 고드름과 같은 얼음 형태는 천천히 떨어지는 물방울에 의해 생성되는데, 물방울은 특히 중력의 영향을 많이 받기 때문에 얼음 표면을 따라 수직으로 흐른다. 따라서 고드름의 수평 성장은 물방울에 남아있는 얇은 수막 으로 인해 발생한다. 반면에 물방울은 접착력과 표면장력으로 인해 비교적 오랫동안 표면에 접착되기 때문에 고드름의 끝 부 분은 수직 방향으로 더 길어진다. 그러나 물방울은 중력보다 강한 바람이나 외력의 영향을 더 많이 받기 때문에 고드름은 앞에서 언급한 환경적 요소를 고려한 방향을 가지고 있게 된 다. 본 논문에서는 급속한 물 동결과정에서 물의 흐름을 사용 하여 얼음의 성장 방향을 이방성하게 모델링한다. 물이 오브 젝트와 충돌하면 물의 속도는 변경되며, 유체 입자의 속도를 활용하여얼음의 성장 방향을 계산한다 (Equation 26 참조).

gv i c e | s o l i d = ∑ j ∈ S (i) f l u i d v j f l u i d W A (x i c e | s o l i d − x j, G j) ‖ S (i) f l u i d ‖

(26)

여기서 gv^ice|solid는 i번째 고체와 얼음 입자의 성장 방향이며, v_j와 S(i)는 유체 입자의 속도와 인접 입자들이다. 선형 변환 G는 방사형 벡터 r을 회전하고 늘리며, 결과적으로 W_A는 이 방성한 가중치커널이다 (Equation 27 참조).

W A (r, G) = σ ‖ G ‖ ‖ Gr ‖

(27)

유체 입자로부터 이방성 커널을 계산하기 위해 우선 공분 산 행렬을 계산하고 (Equation 28 참조), 주성분 분석(Principal component analysis, PCA)를 수행하여 유체 입자들의 방향(Orientation)과 신축(Stretching)을 계산한다. 본 논문에서 PCA 계 산은 SVD(Singular value decomposition)을 통해 계산했으며, 이 를 이용하여 계산한 고유벡터와 고유값은 아래와 같다 (Equation 29 참조).

C f l u i d = ∑ j W i j (x j − x i) (x j − x i) T ∑ j W i j

(28)

G = R Φ R T

(29)

Φ = d i a g (σ 1, σ 2)

(30)

여기서 R은 주축(Principal axes)을이용하여 계산한 회전 행렬 이며, Φ는 고유값이 들어있는 대각 행렬이다. 이 값으로부터 이방성 행렬 G를 계산한다. 결과적으로 이방성 커널인 W_A를 활용하여 얼음의 성장 방향을 계산한다. 오브젝트 표면에 얼음이 형성되기 때문에 유체 입자가 오브젝트와 충돌 할 때 마다 성장 방향 벡터인 gv^ice|solid가계산된다.

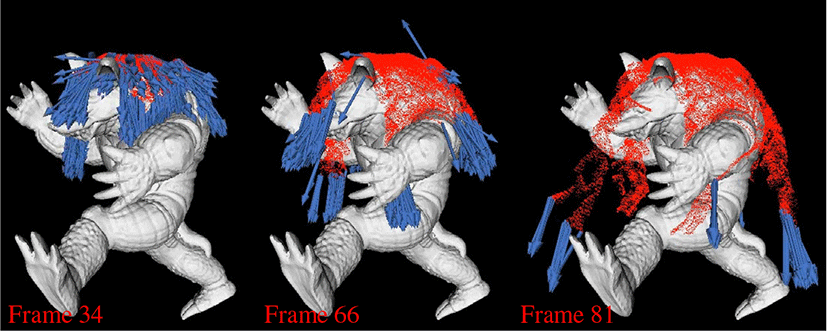
특정 방향으로 얼음을 생성하는 이전 기법들과는달리 제안 하는 방법으로 생성된 얼음은 gv^ice|solid를 이용하여 물의 흐 름 방향에 따라 이방성하게 얼음이 성장한다. Figure 3은 얼음 의 성장 방향을 나타낸 결과이다. 이 그림에서 유체 입자가 오 브젝트와 충돌함으로써 급속한 물 동결이 진행되고, 이 과정 에서성장 방항을 나타내는 화살표는 gv^ice|solid를 의미한다.

Figure 3: Growth direction vector with anisotropic kernel (blue arrow : gv^ice|solid, red particle : ice particle).

Download Original Figure

3.2.3 상태변화

본 논문에서는 gv^ice|solid를 기반으로 유체 입자가 얼음 입자 로 상태변화하는데 영향을 주는 동결 계수를 계산할 수 있는 방법을 제안한다. 만약에 고체 입자 주변에 존재하는 유체 입 자가 같은 동결 계수를 가지고 있다면, 얼음은 같은 방향으로 동일하게 성장하기 때문에 오직 얼음의 글레이즈 효과만 표현 될 것 이다. 우리는 물의 흐름에 따라 동결 효과를 제어하고 싶 기 때문에, 이에 해당하는 동결 계수를 다음과 같이 계산한다 (Equation 31 참조).

f r = ĝ v i c e | s o l i d ⋅ x^i s f

(31)

여기서 fr은 유체 입자의 동결 계수이며, x^isf 는 다음과 같다: x^isf = x^ice|solid − x^fluid. 위 수식에서 각 벡터는 정규벡터 임 $(x^i s f)$ 을 유의해야 한다. Equation 31은 각 유체 입자의 동결 계수가 gv^ice|solid와 x^isf 사이의 각도에 의해 결정된다는 것을 보여준다. 이 각도가 90도를 초과하면 fr은 음수가 되며, fr 값이 음수인 영역에서는 얼음이 자라나지 않는다. 본 논문에 서는 습도가 높고 fr값이 둔각을 갖는 지역에서 얼음이 자라 나도록 fr의 범위를 [0, 1]로 조정하기 위해 fr을 다음과 같이 스케일링 한다 : $f r = f r + 1 2$ .

유체를 얼음으로 변경하려면 핵 생성 과정이 필요하며, 이 핵 생성 에너지는 온도, 습도 및 기타 요인의 영향을 받는 분 자간의 힘이 강해질 때 발생한다. 본 논문에서는 핵 생성 에 너지를 통해 분자간의 힘을 모델링한다. 우리의 목표 모델이 과냉각수(Supercoolded water)이기 때문에 오브젝트의 수온은 이미 0도 미만이라고 가정하고 시뮬레이션을 한다. 오브젝트 가 젖으면 오브젝트 표면에 수막이 나타나기 때문에 습도는 3.2.1장에서 설명한 가상 수막에 의해 근사된다. 결과적으로 본 논문에서 제안하는 이방성한 핵 생성 에너지는 다음과 같 이 계산한다 (Equation 32 참조).

c e (x i i c e | s o l i d, x j f l u i d) = Γ i f r W A (x i − x j, G j)

(32)

여기서 $c e (x i i c e, x j f l u i d)$ 와 $c e (x i s o l i d, x j f l u i d)$ 는 각각 유체와 얼음 입자에 대한핵 생성 에너지를 의미하며, Γ_i는 가상 수막 을 나타낸다. 실제로 얼음 성장을 위한핵 생성 에너지는 주변 환경에 따라 다르게 나타나기 때문에 본 논문에서는 유체와 얼음 입자에 대한 핵 생성 에너지를 독립적으로 계산한다. 또 한, 글레이즈와 고드름 임계값(Icicle threshold)을 사용하여 핵 생성 에너지를 조절함으로써 얼음의 글레이즈와 고드름을 개 별적으로 표현할 수 있다.

고체 입자와 접촉하는 유체 입자의 ce가 글레이즈 임계값 (Glaze threshold)인 gz_th를 초과하면 오브젝트 표면에 생성되 는 글레이즈를 표현하기 위한 얼음 입자로 변환된다. 마찬가 지로, 얼음 입자와 접촉하는 물 입자의 ce가 고드름 임계값인 ic_th를 초과하면 얼음 입자로 변환된다. Figure 4는 유체가 얼음 입자로 상태변화하는 결과이다. 그림에서 보듯이유체 입자가 고체와 충돌됨에 따라 급속 빙결이 진행되며, 앞에서 설명한 알고리즘에 따라 얼음 입자로 변경되는 결과를 보여준다.

Figure 4: Simulation results of changing state from fluid to ice particles (red particle : ice particle).

Download Original Figure

3.2.4 빙결 형태의 품질 개선을 위한 유체의 표면장력, 공기 압력, 점성 추가

얼음의 형태를 모델링하는데 있어 중요한 점은유체의 움직이 며, 유체의 움직임이 비사실적이거나 불안정하게되면 결과적 으로 빙결 시뮬레이션의 품질을 저하시키는 원인이 된다. 우 리는 Im 등이 [5] 제안한 것처럼 유체의 움직임에 표면장력을 추가하여 빙결 시뮬레이션 과정에서 유체 입자가 서로 뭉치는 효과를 표현했다.

유체의 표면장력과공기압력 : Im 등은 [5] Akinci 등의 [34] 표면장력을 사용했지만 수치적으로 불안정하게 수렴하는 문 제가 나타났으며, 본 논문에서는 얼음 입자가 뭉치면서 빙결 되는 형태를 좀 더 잘 표현하고 안정적으로 수렴하는 결과를 얻기 위해 He 등의 방법을 [32] 활용하여 유체 솔버를 개선한 다 (Equation 34 참조).

c (x) = ∑ j m j 1 ρ j W (x − x j, h)

(33)

∇ i c = ∑ j V j c j ∇ i W (x i j, h) ∑ j V j W (x i j, h)

(34)

여기서 V_j는 j번째 유체 입자의 볼륨이며, x_ij는 입자 i와 j 사이의 거리이다. 표면장력인 $F i s$ 를 계산하는 과정에서 운동 량 보존을 보장하기 위해 두 표면장력 에너지 밀도의 평균을 계산하고, 이 항을 표면장력 공식에 사용한다 (Equation 35 참 조).

F i s = κ 4 ∑ j V i V j (| ∇ c i | 2 + | ∇ c j | 2) ∇ i W (x i j, h)

(35)

여기서 κ는 제곱된 기울기 에너지 계수(Squared gradient energy coefficient)이며 [35, 32], 본 논문에서는 0.02로 설정했다.

본 논문에서는 표면에 따라 유체가 흐르면서 빙결되는 효과 를 개선하기 위해 유체 입자들에 대해서 공기압력 힘(Air pressure force)인 $F i a$ 를 추가한다 [32] (Equation 36 참조).

F i a = V i p a t m ∑ j V j ∇ i W (x i j, h)

(36)

여기서 p_atm는 유체 입자의 공기압력(Air pressure)이며, 본 논 문에서는 5000으로 설정했다. 우리가 사용한 표면장력 힘은 앞에서 정의한 두 가지 힘을 모두 사용한다 : $F i s + a = F i s + F i a$ .

Figure 5는 Im 등이 [5] 제안한 방법에서 사용한 표면장력 과 우리가 사용한 표면장력의 결과를 비교한 그림이다. 본 논 문에서 새로운 표면장력 기법을 제안한 것은 아니지만, 최신 연구인 Im 등이 [5] 사용한 표면장력은 불안정한 결과를 만들 어 낼 수 있기에 이 부분을 개선한 것이다. 본 논문에서 사용한 IISPH 해법 내에서 표면장력은 IISPH에서 압력을 계산하기 위 한 반복법(Iterative solver) 내에서 계산되며, 이 힘은 향후 입자 의위치를 업데이트 하는 적분 과정에서 활용된다.

Figure 5: Comparison results of surface tension (inset image : zoom-in).

Download Original Figure

유체의 점성 : Im 등은 [5] Akinci의 표면장력만을 [34] 사 용하여 유체가 흐르면서 빙결될 때 표현되는 곡선형 얼음의 형태를 표현했다. 하지만, 이러한 접근법은 유체의 움직임에 따른 빙결 형태를 모델링하기에 충분하지 않다. 오브젝트와 충돌하는 유체 입자의 속도가 매우 느리다면 오브젝트의 표 면에 따라 흡착하면서 흘러내리기 때문에얼음의 글레이즈나 곡선 형태의 얼음 모델링이 가능하지만, 유체 입자의 속도가 조금이라도 빨라지면 불안정해지기 때문에 사실상 빙결 형태 를 모델링하기 어려워진다.

Figure 6은 Im 등의 [5] 방법을 사용하여 만든 결과이며, 그 림에서 보듯이 입자의 속도가 조금만 빨라져도 유체의 접착 력이나 표면장력이 제대로 표현되지 않고, 오히려 스플래쉬 와 같이 흩날리는 움직임으로 표현되고 이러한 움직임은 빙결 형태에도 영향을 끼친다. 이러한 시뮬레이션 불안정성을 줄이 고 빙결 형태의 품질을 향상시키기 위해 본 논문에서는 표면 장력에 의한 접착력과 응집력 뿐만 아니라 점성인 $F i ∈ f l u i d v f$ 와 $F i ∈ s o l i d v s$ 를 추가한다 (Equations 37과 40 참조).

Figure 6: Simulation of freezing water using Im et al. [] (particle : fluid particle, mesh : ice surface).

Download Original Figure

F i ∈ f l u i d v f = ∑ j m j β 0 u i j β 1 ρ i j a v g ∇ i W (x i j, h)

(37)

u i j = h (v i j ⋅ x i j) ‖ x i j ‖ 2 h 2

(38)

ρ i j a v g = ρ i + ρ j 2

(39)

여기서 β₀와 β₁는 각각 체적 점성계수(Bulk viscosity), 음파 (Sound wave)를 의미하며, 본 논문에서는 0.1과 10으로 설정하 였다. 위 수식은 유체 입자에만 해당되는 점성 효과이기 때문 에 물의 흐름을 끈적하게 만들어 낼 수 있다. 이런 점성 효과는 유체의 표면장력이나 접착력을 더욱더 잘 표현될 수 있도록 도와주기 때문에 (Figure 7 참조), 유체 흐름에 따른 빙결효과 를 더욱더 잘 표현한다. 그림에서도 보듯이 유체가 오른쪽 벽 면에 강하게 충돌했음에도 불구하고 단순하게 표면장력만 사 용한 결과보다 점성과 표면장력이 안정적으로 잘 표현되었다 ((Figures 7c와 7d 참조).

Figure 7: Comparison results of viscosoty force

F i ∈ s o l i d v s

Download Original Figure

$F i ∈ s o l i d v s$ 로 인해 유체의 점성 효과는 표현되지만 얼음의 글 레이즈 효과나 곡선 형태의 빙결을 모델링하기에는 충분하지 않다. 그 이유는 유체 입자가고체 표면과 충돌할 때는 스플래 쉬처럼 흩날리는게 아닌 표면에 따라 끈적이게 붙으면서 흘러 내리는 듯한 움직임이 나타나야 한다. 이 현상은 물리적인 측 면에서도 물이 가지고 있는 온도가 차가운 고체에 닿았을 때, 그 열을 차가운 고체에 흡수되면서 결과적으로 물이 고체 표면 에 붙으면서 흘러내리는 듯한 움직임이 나타난다. Figure 7에 서 보듯이 유체가 벽면에 충돌되고 난 뒤 점성에 의해 유체가 끈적이면서 뭉치는 효과는 잘 표현되지만, 충돌체인 벽면에 끈적이면서 흘러내리는 듯한 움직임은 표현되지 않는다. 이 문제를 해결하기 위해 본 논문에서는 경계 입자를 기반으로 경계 부근에서 추가적인 점성 효과가 표현되도록 $F i ∈ s o l i d v s$ 를 계산한다 (Equation 40 참조).

F i ∈ s o l i d v s = ∑ j ψ j u i j β 1 ρ i j a v g ∇ i W (x i j, h)

(40)

여기서 Ψ_j는 Akinci 등이 [30] 제안한 경계 입자의 볼륨이며, 좀 더 자세한 볼륨의 계산은 Akinci 등의 연구를 참조해보길 추천한다.

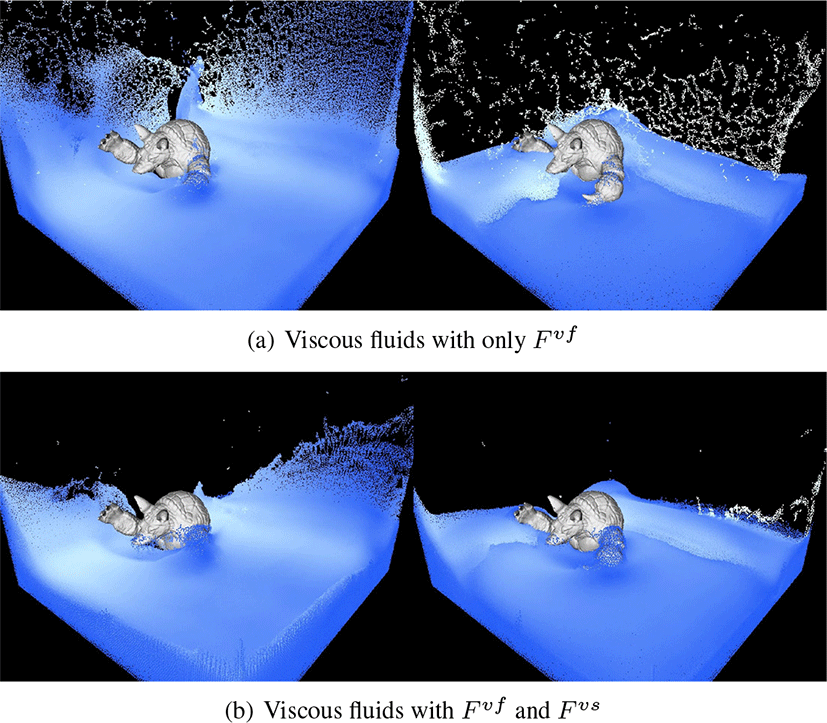
Figure 8은 경계 부근에서의 점성 효과를 보기위해 F^vf 와 F^vs를 비교한 결과이다. 유체의 체적 볼륨만 적용한 결과인 Figure 8a에 비해 Figure 8b는 벽면이나 Armadillo모델 표면에 유체가 끈적이게 흘러 내리는 결과를 더욱더 잘 보여준다. 이 러한 특징은 빙결 형태를 더욱더 사실적으로 표현할 수 있게 도와준다. 유체가 고체와 충돌되어 빙결되는 시점에서 유체 입자가 흩날리게 되면 얼음 형태라기 보다는 노이즈와 같은 얼음 표면이 생성될 가능성이 높지만 (Figure 6의 Frame 51 참 조), 경계 부근에서 발생하는 점성으로 인해 고체 표면에 흘 러가는 유체의 입자는 얼음의 글레이즈 효과나 곡선 형태의 빙결을 안정적으로 잘 표현할 수 있다.

Figure 8: Comparison results of viscosity forces

F i ∈ s o l i d v s

and

F i ∈ s o l i d v s

Download Original Figure

3.2.5 얼음 입자의 표면 복원

얼음의 표면을 복원하는단계에서는 이방성한 얼음 성장의 방 향을 계산할 때 사용한 SVD값을 활용한다. 본 논문에서는 Yu 등이 제안한 알고리즘에 SVD의이방성 특성을재사용해 얼음 의 표면을 디테일하게 재구성하였으며 [36], 얼음 입자의 레벨 셋은 다음과같이 계산한다 (Equation 41 참조).

ϕ (x) = min i (‖ D i i c e (x i − x) ‖)

(41)

여기서 $D i i c e$ 는 얼음 입자 i에 대한 변환행렬을 나타내며, 그 속성을 아래와 같다 (Equation 42 참조).

D i i c e = 1 k s [e 1 T e 2 T e 3 T] T [σ 1 σ 2 σ 3] − 1 [e 1 T e 2 T e 3 T]

(42)

여기서 k_s는 스케일링 상수이며, 변화가가장 큰 신축(Stretching)을 보존하기 위해 σ_n를 일정 범위 내로 제한하였다. 좀 더 자세한 설명은 Yu 등의 연구를 참조해보길 추천한다 [36]. 본 논문에서는 GPU기반 마칭 큐브(Marching Cubes) 알고리즘을 이용하였으며 [37], 얼음 표면이 잘 표현이 되도록 최소 신축 값을 격자 너비의 절반보다 크게 설정하였다.

4. 구현

본 논문은 다음과 같은 환경에서 구현되었다 : 인텔 i7-7700k 4.20GHz CPU, 32GB RAM, NVIDIA GeForce GTX 1080Ti 그 래픽카드. IISPH 기반 유체 해법을 기반액체(Underlying water) 시뮬레이션으로 사용했으며 [29], GPU 환경에서 구현되었다. 얼음 표면 재복원을 위해 격자를 추가적으로 사용하였으며, 유체와 고체의 충돌처리를 위해 Akinci 등이 제안한 경계입자 (Boundary particle) 기법을 사용하였다 [30]. 마칭 큐브 알고리 즘은 200×200×200의 격자 해상도를 이용하여얼음 표면을재 구성하는데 사용했다. 본 논문에서 제안하는 빙결 시뮬레이션 알고리즘의의사코드는다음과같다 (Algorithm 1 참조).

Algorithm 1

Pseudo-Code of Our Algorithm

for each frame do

// Base water solver

Advect 3D water partices using IISPH // Section 3.1

Compute the interaction of water & solids

// Freezing water solver

Viscosity force // Section 3.2.4

Surface tension and air pressure forces // Section 3.2.4

Virtual water film // Section 3.2.1

Anisotropic direction for growthing // Section 3.2.2

Phase transition from water to ice // Section 3.2.3

Ice surface reconstruction // Section 3.2.5

end for

5. 결과

본 논문에서 제안하는 기법을 여러 방면으로 분석하기 위해 다양한 시나리오에서 비교해봤다.

Figure 9는 구형 액체를 Stanford Bunny모델에 떨어뜨리는 장면으로 급속 빙결되는 결과를 보여주고 있다. 이 장면에서 유체를 표현하기 위해 타입 스텝을 0.006으로 설정하고, 약 5 만개의 유체 입자를 사용하였다. 구형 액체가 오브젝트와 충 돌하는 순간 Im 등의 방법은 [5] 스플래쉬처럼 흩날리게 되어 고체 표면에 생성되어야 하는 가상 수막이 제대로 계산되지 못하고, 결과적으로 얼음 표면을 표현하지 못하는 결과로 이 어지게 된다 (Figure 9a의 inset image 참조). 반면에 제안하는 방법은 같은 프레임에서도 고체 표면에 생성되는 얼음의 글 레이즈 효과같은 빙결 형태를 잘 표현했다. 이 후 프레임에서 도 우리의 기법은 글레이즈와 고체 표면에 따라 곡선형태로 빙결되는 얼음의 형태를 잘 표현했다. Im 등의 방법에서도 [5] 얼음은 표현되지만, 흩날리는 유체의 움직임 때문에 오브젝트 표면을 흐르면서 얼어붙는 형태보다는 노이즈 형태로 빙결되 는 결과를 보였다 (Figure 9b 참조).

Figure 9: Freezing water simulations on the Stanford Bunny with our method (inset image : Im et al. [], particle : fluid particle, mesh : ice surface).

Download Original Figure

Figure 10은 경계 부근에서 생성되는 빙결 형태의 품질과 움 직임에 대한 비교를 보여주는 결과이다. Im 등의 방법은 [5] 경계 부근에서도 유체 입자들의 불안정한 움직임 때문에 빙결 형태가 제대로 표현되지 않는 반면 (Figure 10a 참조), 제안하 는 기법은 급속 빙결시 표현되는 얼음의 얇은 막(Thin sheets) 도 잘 생성했으며 경계 부근에서도 안정적으로 빙결 형태를 잘 표현했다 (Figure 10b 참조).

Figure 10: Quality comparison at the boundary region between (a) Im et al. [] and (b) our method (red rectangle : boundary region, particle : fluid particle, mesh : ice surface).

Download Original Figure

Figure 11은 구형 액체를 Armadillo모델에 떨어뜨리는 장면 으로 급속 빙결되는 결과를 보여주고 있다. 중력에 의해 아래 방향으로 빙결되는 과정에서 유체의 움직임에 영향을 받아서 지그재그 형태로 빙결되는 결과를 잘 보여준다. Armadillo모 델의 상단에서는 얼음의 글레이즈 효과가 표현된 반면, Frame 72에서는 고드름처럼 얇은 형태로 얼음이 생성되는 결과를 보 여준다. 이방성한 얼음의 성장 방향인 gv로 인해 빙결 형태 가 방향성있게 퍼지는 결과를 얻을 수 있었다 (Figure 11의 red rectangle 참조).

Figure 11: Freezing water simulations on the Armadillo with our method (mesh : ice surface, red rectangle : anisotropic surfaces of freezing water).

Download Original Figure

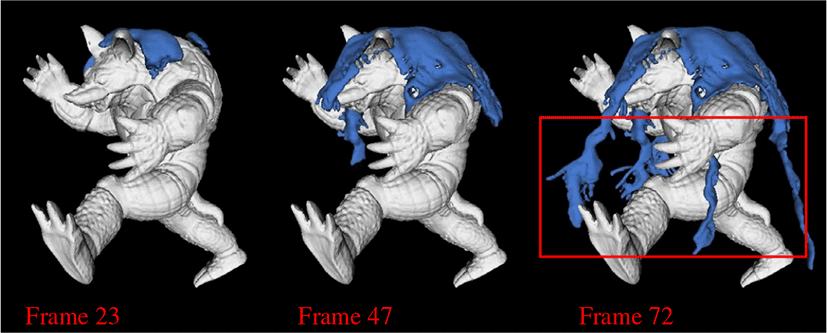
Figure 12는 앞에서 보여준 결과와 마찬가지로 액체를 떨어 뜨리는 장면에서 급속 빙결되는 결과를 보여준다. Im 등의 방 법에서 [5] 보여지듯이 불안정하게 생성되는 빙결 모델링과는 다르게, 제안하는 기법은 얼음의 글레이즈와 유체의 흐름에 따라 곡선형태로 빙결되는 얼음 표면을 사실적으로 잘 표현 했다.

앞에서 보여준 결과들에서도 알 수 있듯이 제안하는 기법은 빙결 시뮬레이션을 안정적이고 사실적으로 잘 표현했고, 최신 빙결 기법인 Im 등의 방법보다 [5] 안정성 및 품질면에서도 나 은 결과를 보여주었다.

6. 결론 및 향후 연구

본 논문에서는 얼음의 디테일한 특징 중 하나인 급속 빙결시 표현되는 얼음의 표면을 안정적이고 사실적으로 표현하기 위 한 프레임워크를 설명했다. 유체의 흐름에 따라 방향성 있게 얼음을 성장시키기 위해 이방성 기반으로 얼음의 성장 방향을 계산했고, 얼음의 글레이즈와 곡선형 빙결 형태를 더욱더 잘 표현하기 위해 유체의 움직임에 표면장력, 공기압력, 점성을 추가하여 빙결 모델링의 안정성을 개선시켰다. 제안된 방법 은 특정 장면에서만 급속 빙결을 표현했던 기존의 기법과는 달리, 다양한 장면에서 모두 안정적으로 개선된 빙결 결과를 보여주었다. 뿐만 아니라, 빠른 유속에서 스플래쉬처럼 흩날 려버리는 유체 입자는 얼음 모델링에도 영향을 주어 빙결을 표현하는데 있서 안정성 문제를 야기시켰지만 (Figure 12 참 조), 동일한프레임에서도 우리의 방법은 훨씬 나은 결과를 보 여주었다.

Figure 12: Freezing water simulations on the Utah Teapot with our method (particle : fluid particle, mesh : ice surface, inset image : Im et al. []).

Download Original Figure

향후, 유체 입자를 이용하지 않고 주변 공기 또는 바람의 흐 름만을이용하여 빙결 시뮬레이션을 효율적으로 표현할 수 있 는 방법에 대해 연구할 계획이다. 디테일한 곡선형 얼음 표면 을 표현하는데 있어서 유체의 흐름은 중요한 요소지만, 계산 양이 크기 때문에 이를 효율적으로 처리할 수 있는 방법에 대 해서 연구할 계획이다. 또한, 차가운 오브젝트에 물이나 얼음 이 붙어서 표현되는 글레이즈 모델을 물리 기반 현상인 열전달 기반으로 표현할 수 있는 방법에 대해서도 연구할 것이다.

감사의 글

본 연구는 2020학년도 강남대학교교내연구비 지원에 의해 수 행되었음.

참고 문헌

[1].

J. Im, H. Park, J.-H. Kim, and C.-H. Kim, “A particle-grid method for opaque ice formation,” in Computer Graphics Forum, vol. 32, no. 2pt3. Wiley Online Library, 2013, pp. 371–377.

[2].

D. Kharitonsky and J. Gonczarowski, “A physically based model for icicle growth,” The Visual Computer, vol. 10, no. 2, pp. 88–100, 1993.

[3].

T. Kim, D. Adalsteinsson, and M. C. Lin, “Modeling ice dynamics as a thin-film stefan problem,” in Proceedings of the 2006 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2006, pp. 167–176.

[4].

J. Gagnon and E. Paquette, “Procedural and interactive icicle modeling,” The Visual Computer, vol. 27, no. 6-8, p. 451, 2011.

[5].

J. Im, J.-H. Kim, W. Kim, N. Park, T. Kim, Y. B. Kim, J. Lee, and C.-H. Kim, “Visual simulation of rapidly freezing water based on crystallization,” Computer Animation and Virtual Worlds, vol. 28, no. 3-4, p. e1767, 2017.

[6].

T. Kim, M. Henson, and M. C. Lin, “A hybrid algorithm for modeling ice formation,” in Proceedings of the 2004 ACM SIGGRAPH/Eurographics symposium on Computer animation, 2004, pp. 305–314.

[7].

T. Nishino, K. Iwasaki, Y. Dobashi, and T. Nishita, “Visual simulation of freezing ice with air bubbles,” in SIGGRAPH Asia 2012 Technical Briefs, 2012, pp. 1–4.

[8].

J.-H. Kim, J. Im, C.-H. Kim, and J. Lee, “Subtle features of ice with cloudy effects and scratches from collision damage,” Computer Animation and Virtual Worlds, vol. 27, no. 3-4, pp. 271–279, 2016.

[9].

T. Ishikawa, Y. Dobashi, Y. Yue, M. Kakimoto, T. Watanabe, K. Kondo, K. Iwasaki, and T. Nishita, “Visual simulation of glazed frost,” in ACM SIGGRAPH 2013 Posters, 2013, pp. 1–1.

[10].

Y. Miao and S. Xiao, “Particle-based ice freezing simulation,” in Proceedings of the 14th ACM SIGGRAPH International Conference on Virtual Reality Continuum and its Applications in Industry, 2015, pp. 17–22.

[11].

K. Iwasaki, H. Uchida, Y. Dobashi, and T. Nishita, “Fast particle-based visual simulation of ice melting,” in Computer graphics forum, vol. 29, no. 7. Wiley Online Library, 2010, pp. 2215–2223.

[12].

M. Wicke, P. Hatt, M. Pauly, M. Müller, and M. H. Gross, “Versatile virtual materials using implicit connectivity.” in SPBG, 2006, pp. 137–144.

[13].

L. Makkonen, “A model of icicle growth,” Journal of Glaciology, vol. 34, no. 116, pp. 64–70, 1988.

[14].

L. ”Makkonen, “Models for the growth of rime, glaze, icicles and wet snow on structures,” Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, vol. 358, no. 1776, pp. 2913–2939, 2000.

[15].

G. Meschke, C. Liu, and H. A. Mang, “Large strain finite-element analysis of snow,” Journal of engineering mechanics, vol. 122, no. 7, pp. 591–602, 1996.

[16].

A. Stomakhin, C. Schroeder, L. Chai, J. Teran, and A. Selle, “A material point method for snow simulation,” ACM Transactions on Graphics (TOG), vol. 32, no. 4, pp. 1–10, 2013.

[17].

A. P. Tampubolon, T. Gast, G. Klár, C. Fu, J. Teran, C. Jiang, and K. Museth, “Multi-species simulation of porous sand and water mixtures,” ACM Transactions on Graphics (TOG), vol. 36, no. 4, pp. 1–11, 2017.

[18].

J. Wretborn, R. Armiento, and K. Museth, “Animation of crack propagation by means of an extended multi-body solver for the material point method,” Computers & Graphics, vol. 69, pp. 131–139, 2017.

[19].

M. Gao, X. Wang, K. Wu, A. Pradhana, E. Sifakis, C. Yuksel, and C. Jiang, “Gpu optimization of material point methods,” ACM Transactions on Graphics (TOG), vol. 37, no. 6, pp. 1–12, 2018.

[20].

Y. Fang, M. Li, M. Gao, and C. Jiang, “Silly rubber: an implicit material point method for simulating non-equilibrated viscoelastic and elastoplastic solids,” ACM Transactions on Graphics (TOG), vol. 38, no. 4, pp. 1–13, 2019.

[21].

S. Wang, M. Ding, T. F. Gast, L. Zhu, S. Gagniere, C. Jiang, and J. M. Teran, “Simulation and visualization of ductile fracture with the material point method,” Proceedings of the ACM on Computer Graphics and Interactive Techniques, vol. 2, no. 2, pp. 1–20, 2019.

[22].

X. Han, T. F. Gast, Q. Guo, S. Wang, C. Jiang, and J. Teran, “A hybrid material point method for frictional contact with diverse materials,” Proceedings of the ACM on Computer Graphics and Interactive Techniques, vol. 2, no. 2, pp. 1–24, 2019.

[23].

S.-K. Wong and I.-T. Fu, “Hybrid-based snow simulation and snow rendering with shell textures,” Computer Animation and Virtual Worlds, vol. 26, no. 3-4, pp. 413–421, 2015.

[24].

N. Mukai, Y. Eto, and Y. Chang, “Representation method of snow splitting and sliding on a roof,” in 5th International Conference on Advances in Engineering and Technology, 2017, pp. 100–103.

[25].

F. Dagenais, J. Gagnon, and E. Paquette, “An efficient layered simulation workflow for snow imprints,” The Visual Computer, vol. 32, no. 6-8, pp. 881–890, 2016.

[26].

T. Takahashi and I. Fujishiro, “Particle-based simulation of snow trampling taking sintering effect into account,” in ACM SIGGRAPH 2012 Posters, 2012, pp. 1–1.

[27].

A. M. Abdelrazek, I. Kimura, and Y. Shimizu, “Numerical simulation of a small-scale snow avalanche tests using non-newtonian sph model,” Transactions of the Japan Society of Civil Engineers, vol. 70, no. 2, pp. 681–690, 2014.

[28].

P. Goswami, C. Markowicz, and A. Hassan, “Real-time particle-based snow simulation on the gpu,” in EGPGV 2019. Eurographics-European Association for Computer Graphics, 2019.

[29].

M. Ihmsen, J. Cornelis, B. Solenthaler, C. Horvath, and M. Teschner, “Implicit incompressible sph,” IEEE transactions on visualization and computer graphics, vol. 20, no. 3, pp. 426–435, 2013.

[30].

N. Akinci, J. Cornelis, G. Akinci, and M. Teschner, “Coupling elastic solids with smoothed particle hydrodynamics fluids,” Computer Animation and Virtual Worlds, vol. 24, no. 3-4, pp. 195–203, 2013.

[31].

N. Akinci, M. Ihmsen, G. Akinci, B. Solenthaler, and M. Teschner, “Versatile rigid-fluid coupling for incompressible sph,” ACM Transactions on Graphics (TOG), vol. 31, no. 4, pp. 1–8, 2012.

[32].

X. He, H. Wang, F. Zhang, H. Wang, G. Wang, and K. Zhou, “Robust simulation of small-scale thin features in sph-based free surface flows,” ACM Trans. Graph, vol. 34, no. 1, p. 7, 2013.

[33].

S.-Y. Lii and S.-K. Wong, “Ice melting simulation with water flow handling,” The Visual Computer, vol. 30, no. 5, pp. 531–538, 2014.

[34].

N. Akinci, G. Akinci, and M. Teschner, “Versatile surface tension and adhesion for sph fluids,” ACM Transactions on Graphics (TOG), vol. 32, no. 6, pp. 1–8, 2013.

[35].

J. W. Cahn and J. E. Hilliard, “Free energy of a nonuniform system. i. interfacial free energy,” The Journal of chemical physics, vol. 28, no. 2, pp. 258–267, 1958.

[36].

J. Yu and G. Turk, “Reconstructing surfaces of particle-based fluids using anisotropic kernels,” ACM Transactions on Graphics (TOG), vol. 32, no. 1, pp. 1–12, 2013.

[37].

C. Dyken and G. Ziegler, “Gpu-accelerated data expansion for the marching cubes algorithm,” in Proc. PGU Technology Conf, 2010, pp. 115–123.

<저자소개>

김종현

jkcgs-26-5-1-g13

2008년 세종대학교 컴퓨터학과 학사
2010년 고려대학교 컴퓨터학과 석사
2016년 고려대학교 컴퓨터학과 박사
2013년~2016년 (주)텐일레븐 선임연구원
2017년~2020년 강남대학교 소프트웨어응용학부 조교수
2020년~현재 강남대학교 소프트웨어응용학부 부교수
관심분야 : 물리 기반 시뮬레이션, 가상/증강현실, 지오메트리 프로세싱, 게임 물리, 게임 AI